Barrio (matemáticas)

En topología y áreas relacionadas de las matemáticas , un vecindario (o vecindad ) es uno de los conceptos básicos en un espacio topológico . Está estrechamente relacionado con los conceptos de conjunto abierto e interior . Intuitivamente hablando, un vecindario de un punto es un conjunto de puntos que contiene ese punto donde uno puede moverse cierta cantidad en cualquier dirección alejándose de ese punto sin salir del conjunto.

Si es un espacio topológico y es un punto en entonces un vecindario ^[1] de es un subconjunto de que incluye un conjunto abierto que contiene ,${\estilo de visualización X}$${\estilo de visualización p}$${\estilo de visualización X,}$${\estilo de visualización p}$${\estilo de visualización V}$${\estilo de visualización X}$ ${\estilo de visualización U}$${\estilo de visualización p}$$${\displaystyle p\en U\subseteq V\subseteq X.}$$

Esto es equivalente al punto que pertenece al interior topológico de en${\displaystyle p\en X}$${\estilo de visualización V}$${\estilo de visualización X.}$

El vecindario no necesita ser un subconjunto abierto de Cuando es abierto (resp. cerrado, compacto, etc.) en él se llama un${\estilo de visualización V}$${\estilo de visualización X.}$${\estilo de visualización V}$${\estilo de visualización X,}$Vecindario abierto ^[2](resp. vecindario cerrado, vecindario compacto, etc.). Algunos autores^[3]exigen que los vecindarios sean abiertos, por lo que es importante tener en cuenta sus convenciones.

Un conjunto que es un vecindario de cada uno de sus puntos es abierto ya que puede expresarse como la unión de conjuntos abiertos que contienen cada uno de sus puntos. Un rectángulo cerrado, como se ilustra en la figura, no es un vecindario de todos sus puntos; los puntos en los bordes o esquinas del rectángulo no están contenidos en ningún conjunto abierto que esté contenido dentro del rectángulo.

El conjunto de todos los vecindarios de un punto se denomina sistema de vecindarios en el punto.

Si es un subconjunto de un espacio topológico , entonces un vecindario de es un conjunto que incluye un conjunto abierto que contiene , De ello se deduce que un conjunto es un vecindario de si y solo si es un vecindario de todos los puntos en Además, es un vecindario de si y solo si es un subconjunto del interior de Un vecindario de que también es un subconjunto abierto de se llama${\estilo de visualización S}$${\estilo de visualización X}$${\estilo de visualización S}$${\estilo de visualización V}$${\estilo de visualización U}$${\estilo de visualización S}$$${\displaystyle S\subseteq U\subseteq V\subseteq X.}$$${\estilo de visualización V}$${\estilo de visualización S}$${\estilo de visualización S.}$${\estilo de visualización V}$${\estilo de visualización S}$ ${\estilo de visualización S}$${\estilo de visualización V.}$${\estilo de visualización S}$${\estilo de visualización X}$vecindad abierta de La vecindad de un punto es sólo un caso especial de esta definición.${\estilo de visualización S.}$

En un espacio métrico un conjunto es un vecindario de un punto si existe una bola abierta con centro y radio tal que está contenida en${\displaystyle M=(X,d),}$${\estilo de visualización V}$${\estilo de visualización p}$${\estilo de visualización p}$${\displaystyle r>0,}$$${\displaystyle B_{r}(p)=B(p;r)=\{x\en X:d(x,p)<r\}}$$${\estilo de visualización V.}$

${\estilo de visualización V}$Se denomina vecindad uniforme de un conjunto si existe un número positivo tal que para todos los elementos de está contenido en${\estilo de visualización S}$${\estilo de visualización r}$${\estilo de visualización p}$${\estilo de visualización S,}$$${\displaystyle B_{r}(p)=\{x\en X:d(x,p)<r\}}$$${\estilo de visualización V.}$

Bajo la misma condición, para la vecindad de un conjunto es el conjunto de todos los puntos en que están a una distancia menor que de (o equivalentemente, es la unión de todas las bolas abiertas de radio que están centradas en un punto en ):${\displaystyle r>0,}$${\estilo de visualización r}$ $Estilo de visualización S_{r}$${\estilo de visualización S}$${\estilo de visualización X}$${\estilo de visualización r}$${\estilo de visualización S}$$Estilo de visualización S_{r}$${\estilo de visualización r}$${\estilo de visualización S}$$${\displaystyle S_{r}=\bigcup \limits _{p\in {}S}B_{r}(p).}$$

De ello se deduce directamente que un -vecindario es un vecindario uniforme, y que un conjunto es un vecindario uniforme si y sólo si contiene un -vecindario para algún valor de${\estilo de visualización r}$${\estilo de visualización r}$${\estilo de visualización r.}$

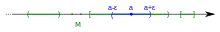
Dado el conjunto de números reales con la métrica euclidiana habitual y un subconjunto definido como entonces es un vecindario para el conjunto de números naturales , pero no es un vecindario uniforme de este conjunto.${\displaystyle \mathbb {R}}$${\estilo de visualización V}$$${\displaystyle V:=\bigcup _{n\in \mathbb {N}}B\left(n\,;\,1/n\right),}$$${\estilo de visualización V}$${\displaystyle \mathbb {N}}$

La definición anterior es útil si ya se ha definido el concepto de conjunto abierto . Existe una forma alternativa de definir una topología: primero se define el sistema de vecindad y luego los conjuntos abiertos como aquellos conjuntos que contienen una vecindad de cada uno de sus puntos.

Un sistema de vecindad es la asignación de un filtro de subconjuntos de a cada uno de tal manera que${\estilo de visualización X}$ ${\estilo de visualización N(x)}$${\estilo de visualización X}$${\estilo de visualización x}$${\estilo de visualización X,}$

1. El punto es un elemento de cada uno en${\estilo de visualización x}$${\estilo de visualización U}$${\estilo de visualización N(x)}$
2. cada en contiene algunos en tal que para cada en es en${\estilo de visualización U}$${\estilo de visualización N(x)}$${\estilo de visualización V}$${\estilo de visualización N(x)}$${\estilo de visualización y}$${\estilo de visualización V,}$ ${\estilo de visualización U}$${\displaystyle N(y).}$

Se puede demostrar que ambas definiciones son compatibles, es decir, la topología obtenida a partir del sistema de vecindad definido mediante conjuntos abiertos es la original, y viceversa cuando se parte de un sistema de vecindad.

En un espacio uniforme se llama vecindad uniforme de si existe un entorno tal que contiene todos los puntos de que son -cercanos a algún punto de que es, para todo${\displaystyle S=(X,\Phi ),}$ ${\estilo de visualización V}$${\estilo de visualización P}$ ${\displaystyle U\in \Phi }$${\estilo de visualización V}$${\estilo de visualización X}$${\estilo de visualización U}$${\estilo de visualización P;}$${\displaystyle U[x]\subseteq V}$${\displaystyle x\en P.}$

Un vecindario eliminado de un punto (a veces llamado vecindario perforado ) es un vecindario de sin Por ejemplo, el intervalo es un vecindario de en la línea real , por lo que el conjunto es un vecindario eliminado de Un vecindario eliminado de un punto dado no es de hecho un vecindario del punto. El concepto de vecindario eliminado aparece en la definición del límite de una función y en la definición de puntos límite (entre otras cosas). ^[4]${\estilo de visualización p}$${\estilo de visualización p,}$${\displaystyle \{p\}.}$ ${\displaystyle (-1,1)=\{y:-1<y<1\}}$${\displaystyle p=0}$${\displaystyle (-1,0)\cup (0,1)=(-1,1)\setminus \{0\}}$${\estilo de visualización 0.}$

• Punto aislado  – Punto de un subconjunto S alrededor del cual no hay otros puntos de S
• Sistema de vecindad  – (para un punto x) conjunto de todas las vecindades para el punto xPáginas que muestran descripciones de wikidata como alternativa
• Región (matemáticas)  – Subconjunto abierto conexo de un espacio topológicoPáginas que muestran descripciones breves de los objetivos de redireccionamiento
• Vecindario tubular  : vecindario de una subvariedad homeomorfa al fibrado normal de esa subvariedadPáginas que muestran descripciones de wikidata como alternativa

• Bredon, Glen E. (1993). Topología y geometría . Nueva York: Springer-Verlag. ISBN. 0-387-97926-3.
• Engelking, Ryszard (1989). Topología general . Heldermann Verlag, Berlín. ISBN 3-88538-006-4.
• Kaplansky, Irving (2001). Teoría de conjuntos y espacios métricos . Sociedad Matemática Americana. ISBN 0-8218-2694-8.
• Kelley, John L. (1975). Topología general . Nueva York: Springer-Verlag. ISBN. 0-387-90125-6.
• Willard, Stephen (2004) [1970]. Topología general. Mineola, NY : Dover Publications . ISBN 978-0-486-43479-7.OCLC 115240  .