Producto escalar

En matemáticas , el producto escalar o producto escalar ^{[nota 1]} es una operación algebraica que toma dos secuencias de números de igual longitud (generalmente vectores de coordenadas ) y devuelve un solo número. En geometría euclidiana , el producto escalar de las coordenadas cartesianas de dos vectores se usa ampliamente. A menudo se lo llama producto interno (o raramente producto de proyección ) del espacio euclidiano , aunque no es el único producto interno que se puede definir en el espacio euclidiano (consulte Espacio de producto interno para obtener más información).

Algebraicamente, el producto escalar es la suma de los productos de las entradas correspondientes de las dos secuencias de números. Geométricamente, es el producto de las magnitudes euclidianas de los dos vectores y el coseno del ángulo entre ellos. Estas definiciones son equivalentes cuando se utilizan coordenadas cartesianas. En la geometría moderna , los espacios euclidianos se definen a menudo mediante el uso de espacios vectoriales . En este caso, el producto escalar se utiliza para definir longitudes (la longitud de un vector es la raíz cuadrada del producto escalar del vector por sí mismo) y ángulos (el coseno del ángulo entre dos vectores es el cociente de su producto escalar por el producto de sus longitudes).

El nombre "producto escalar" se deriva del operador de punto "  ·  ", que a menudo se utiliza para designar esta operación; ^[1] el nombre alternativo "producto escalar" enfatiza que el resultado es un escalar , en lugar de un vector (como con el producto vectorial en el espacio tridimensional).

El producto escalar puede definirse algebraica o geométricamente. La definición geométrica se basa en las nociones de ángulo y distancia (magnitud) de los vectores. La equivalencia de estas dos definiciones depende de que exista un sistema de coordenadas cartesianas para el espacio euclidiano.

En las presentaciones modernas de la geometría euclidiana , los puntos del espacio se definen en términos de sus coordenadas cartesianas , y el espacio euclidiano en sí mismo se identifica comúnmente con el espacio de coordenadas reales . En una presentación de este tipo, las nociones de longitud y ángulo se definen por medio del producto escalar. La longitud de un vector se define como la raíz cuadrada del producto escalar del vector por sí mismo, y el coseno del ángulo (no orientado) entre dos vectores de longitud uno se define como su producto escalar. Por lo tanto, la equivalencia de las dos definiciones del producto escalar es parte de la equivalencia de las formulaciones clásica y moderna de la geometría euclidiana.${\displaystyle \mathbf {R} ^{n}}$

El producto escalar de dos vectores y , especificado con respecto a una base ortonormal , se define como: ^[2]${\displaystyle \mathbf {a} = [a_{1},a_{2},\cdots ,a_{n}]}$${\displaystyle \mathbf {b} = [b_{1},b_{2},\cdots ,b_{n}]}$

$${\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}$$

donde denota sumatoria y es la dimensión del espacio vectorial . Por ejemplo, en el espacio tridimensional , el producto escalar de los vectores y es:${\estilo de visualización \Sigma}$${\estilo de visualización n}$${\displaystyle [1,3,-5]}$${\displaystyle [4,-2,-1]}$

$${\displaystyle {\begin{aligned}\ [1,3,-5]\cdot [4,-2,-1]&=(1\times 4)+(3\times -2)+(-5\times -1)\\&=4-6+5\\&=3\end{aligned}}}$$

Del mismo modo, el producto escalar del vector consigo mismo es:${\displaystyle [1,3,-5]}$

$${\displaystyle {\begin{aligned}\ [1,3,-5]\cdot [1,3,-5]&=(1\times 1)+(3\times 3)+(-5\times -5)\\&=1+9+25\\&=35\end{aligned}}}$$

Si los vectores se identifican con vectores columna , el producto escalar también se puede escribir como un producto matricial.

$${\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {a} ^{\mathsf {T}}\mathbf {b} ,}$$donde denota la transpuesta de .${\displaystyle a{^{\mathsf {T}}}}$${\displaystyle \mathbf {a}}$

Expresando el ejemplo anterior de esta manera, una matriz 1 × 3 ( vector fila ) se multiplica por una matriz 3 × 1 ( vector columna ) para obtener una matriz 1 × 1 que se identifica con su entrada única:$${\displaystyle {\begin{bmatrix}1&3&-5\end{bmatrix}}{\begin{bmatrix}4\\-2\\-1\end{bmatrix}}=3\,.}$$

En el espacio euclidiano , un vector euclidiano es un objeto geométrico que posee tanto una magnitud como una dirección. Un vector puede representarse como una flecha. Su magnitud es su longitud y su dirección es la dirección a la que apunta la flecha. La magnitud de un vector se denota por . El producto escalar de dos vectores euclidianos y se define por ^{[3] [4] [1]} donde es el ángulo entre y .${\displaystyle \mathbf {a}}$${\displaystyle \izquierda\|\mathbf {a} \derecha\|}$${\displaystyle \mathbf {a}}$${\displaystyle \mathbf {b}}$$${\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\cos \theta ,}$$${\displaystyle \theta }$${\displaystyle \mathbf {a} }$${\displaystyle \mathbf {b} }$

En particular, si los vectores y son ortogonales (es decir, su ángulo es o ), entonces , lo que implica que${\displaystyle \mathbf {a} }$${\displaystyle \mathbf {b} }$${\displaystyle {\frac {\pi }{2}}}$${\displaystyle 90^{\circ }}$${\displaystyle \cos {\frac {\pi }{2}}=0}$

$${\displaystyle \mathbf {a} \cdot \mathbf {b} =0.}$$En el otro extremo, si son codireccionales , entonces el ángulo entre ellos es cero con y Esto implica que el producto escalar de un vector consigo mismo es lo que da la fórmula para la longitud euclidiana del vector.${\displaystyle \cos 0=1}$$${\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|}$$${\displaystyle \mathbf {a} }$$${\displaystyle \mathbf {a} \cdot \mathbf {a} =\left\|\mathbf {a} \right\|^{2},}$$$${\displaystyle \left\|\mathbf {a} \right\|={\sqrt {\mathbf {a} \cdot \mathbf {a} }},}$$

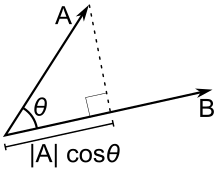
La proyección escalar (o componente escalar) de un vector euclidiano en la dirección de un vector euclidiano está dada por donde es el ángulo entre y .${\displaystyle \mathbf {a} }$${\displaystyle \mathbf {b} }$$${\displaystyle a_{b}=\left\|\mathbf {a} \right\|\cos \theta ,}$$${\displaystyle \theta }$${\displaystyle \mathbf {a} }$${\displaystyle \mathbf {b} }$

En términos de la definición geométrica del producto escalar, esto se puede reescribir como donde es el vector unitario en la dirección de .$${\displaystyle a_{b}=\mathbf {a} \cdot {\widehat {\mathbf {b} }},}$$${\displaystyle {\widehat {\mathbf {b} }}=\mathbf {b} /\left\|\mathbf {b} \right\|}$${\displaystyle \mathbf {b} }$

El producto escalar se caracteriza geométricamente por ^[5] El producto escalar, definido de esta manera, es homogéneo bajo escalamiento en cada variable, lo que significa que para cualquier escalar , también satisface la ley distributiva , lo que significa que$${\displaystyle \mathbf {a} \cdot \mathbf {b} =a_{b}\left\|\mathbf {b} \right\|=b_{a}\left\|\mathbf {a} \right\|.}$$${\displaystyle \alpha }$$${\displaystyle (\alpha \mathbf {a} )\cdot \mathbf {b} =\alpha (\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot (\alpha \mathbf {b} ).}$$$${\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .}$$

Estas propiedades se pueden resumir diciendo que el producto escalar es una forma bilineal . Además, esta forma bilineal es definida positiva , lo que significa que nunca es negativa y es cero si y solo si , el vector cero.${\displaystyle \mathbf {a} \cdot \mathbf {a} }$${\displaystyle \mathbf {a} =\mathbf {0} }$

Si son los vectores base estándar en , entonces podemos escribir Los vectores son una base ortonormal , lo que significa que tienen longitud unitaria y forman ángulos rectos entre sí. Como estos vectores tienen longitud unitaria y forman ángulos rectos entre sí, si , Por lo tanto, en general, podemos decir que: donde es el delta de Kronecker .${\displaystyle \mathbf {e} _{1},\cdots ,\mathbf {e} _{n}}$${\displaystyle \mathbf {R} ^{n}}$$${\displaystyle {\begin{aligned}\mathbf {a} &=[a_{1},\dots ,a_{n}]=\sum _{i}a_{i}\mathbf {e} _{i}\\\mathbf {b} &=[b_{1},\dots ,b_{n}]=\sum _{i}b_{i}\mathbf {e} _{i}.\end{aligned}}}$$${\displaystyle \mathbf {e} _{i}}$$${\displaystyle \mathbf {e} _{i}\cdot \mathbf {e} _{i}=1}$$${\displaystyle i\neq j}$$${\displaystyle \mathbf {e} _{i}\cdot \mathbf {e} _{j}=0.}$$$${\displaystyle \mathbf {e} _{i}\cdot \mathbf {e} _{j}=\delta _{ij},}$$${\displaystyle \delta _{ij}}$

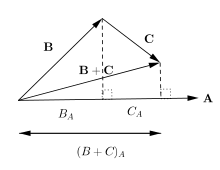
Además, por la definición geométrica, para cualquier vector y un vector , notamos que donde es el componente del vector en la dirección de . El último paso en la igualdad se puede ver en la figura.${\displaystyle \mathbf {e} _{i}}$${\displaystyle \mathbf {a} }$$${\displaystyle \mathbf {a} \cdot \mathbf {e} _{i}=\left\|\mathbf {a} \right\|\,\left\|\mathbf {e} _{i}\right\|\cos \theta _{i}=\left\|\mathbf {a} \right\|\cos \theta _{i}=a_{i},}$$${\displaystyle a_{i}}$${\displaystyle \mathbf {a} }$${\displaystyle \mathbf {e} _{i}}$

Ahora, al aplicar la distributividad de la versión geométrica del producto escalar, se obtiene que es precisamente la definición algebraica del producto escalar. Por lo tanto, el producto escalar geométrico es igual al producto escalar algebraico.$${\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {a} \cdot \sum _{i}b_{i}\mathbf {e} _{i}=\sum _{i}b_{i}(\mathbf {a} \cdot \mathbf {e} _{i})=\sum _{i}b_{i}a_{i}=\sum _{i}a_{i}b_{i},}$$

El producto escalar cumple las siguientes propiedades si , , y son vectores reales y , y son escalares . ^{[2] [3]}${\displaystyle \mathbf {a} }$${\displaystyle \mathbf {b} }$${\displaystyle \mathbf {c} }$${\displaystyle r}$${\displaystyle c_{1}}$${\displaystyle c_{2}}$

Conmutativo

$${\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} ,}$$lo cual se desprende de la definición ( es el ángulo entre y ): ^[6]${\displaystyle \theta }$${\displaystyle \mathbf {a} }$${\displaystyle \mathbf {b} }$ $${\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\cos \theta =\left\|\mathbf {b} \right\|\left\|\mathbf {a} \right\|\cos \theta =\mathbf {b} \cdot \mathbf {a} .}$$

Distributiva sobre suma vectorial

$${\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .}$$

Bilineal

$${\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).}$$

Multiplicación escalar

$${\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=c_{1}c_{2}(\mathbf {a} \cdot \mathbf {b} ).}$$

No asociativo

porque el producto escalar entre un escalar y un vector no está definido, lo que significa que las expresiones involucradas en la propiedad asociativa, o están ambas mal definidas. ^[7] Nótese, sin embargo, que la propiedad de multiplicación escalar mencionada anteriormente a veces se denomina "ley asociativa para producto escalar y escalar" ^[8] o se puede decir que "el producto escalar es asociativo con respecto a la multiplicación escalar" porque . ^[9]${\displaystyle \mathbf {a} \cdot \mathbf {b} }$${\displaystyle \mathbf {c} }$${\displaystyle (\mathbf {a} \cdot \mathbf {b} )\cdot \mathbf {c} }$${\displaystyle \mathbf {a} \cdot (\mathbf {b} \cdot \mathbf {c} )}$${\displaystyle c(\mathbf {a} \cdot \mathbf {b} )=(c\mathbf {a} )\cdot \mathbf {b} =\mathbf {a} \cdot (c\mathbf {b} )}$

Ortogonal

Dos vectores distintos de cero y son ortogonales si y sólo si .${\displaystyle \mathbf {a} }$${\displaystyle \mathbf {b} }$${\displaystyle \mathbf {a} \cdot \mathbf {b} =0}$

Sin cancelación

A diferencia de la multiplicación de números ordinarios, donde si , entonces siempre es igual a menos que sea cero, el producto escalar no obedece la ley de cancelación :${\displaystyle ab=ac}$${\displaystyle b}$${\displaystyle c}$${\displaystyle a}$

Si y , entonces podemos escribir: por la ley distributiva ; el resultado anterior dice que esto simplemente significa que es perpendicular a , lo que todavía permite , y por lo tanto permite .${\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {a} \cdot \mathbf {c} }$${\displaystyle \mathbf {a} \neq \mathbf {0} }$${\displaystyle \mathbf {a} \cdot (\mathbf {b} -\mathbf {c} )=0}$${\displaystyle \mathbf {a} }$${\displaystyle (\mathbf {b} -\mathbf {c} )}$${\displaystyle (\mathbf {b} -\mathbf {c} )\neq \mathbf {0} }$${\displaystyle \mathbf {b} \neq \mathbf {c} }$

Regla del producto

Si y son funciones diferenciables con valores vectoriales , entonces la derivada ( denotada por un primo ) de está dada por la regla${\displaystyle \mathbf {a} }$${\displaystyle \mathbf {b} }$ ${\displaystyle {}'}$${\displaystyle \mathbf {a} \cdot \mathbf {b} }$$${\displaystyle (\mathbf {a} \cdot \mathbf {b} )'=\mathbf {a} '\cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {b} '.}$$

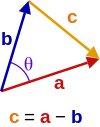
Dados dos vectores y separados por un ángulo (ver la imagen superior), forman un triángulo con un tercer lado . Sean , y las longitudes de , , y , respectivamente. El producto escalar de esto consigo mismo es:${\displaystyle {\color {red}\mathbf {a} }}$${\displaystyle {\color {blue}\mathbf {b} }}$${\displaystyle \theta }$${\displaystyle {\color {orange}\mathbf {c} }={\color {red}\mathbf {a} }-{\color {blue}\mathbf {b} }}$${\displaystyle a}$${\displaystyle b}$${\displaystyle c}$${\displaystyle {\color {red}\mathbf {a} }}$${\displaystyle {\color {blue}\mathbf {b} }}$${\displaystyle {\color {orange}\mathbf {c} }}$

$${\displaystyle {\begin{aligned}\mathbf {\color {orange}c} \cdot \mathbf {\color {orange}c} &=(\mathbf {\color {red}a} -\mathbf {\color {blue}b} )\cdot (\mathbf {\color {red}a} -\mathbf {\color {blue}b} )\\&=\mathbf {\color {red}a} \cdot \mathbf {\color {red}a} -\mathbf {\color {red}a} \cdot \mathbf {\color {blue}b} -\mathbf {\color {blue}b} \cdot \mathbf {\color {red}a} +\mathbf {\color {blue}b} \cdot \mathbf {\color {blue}b} \\&={\color {red}a}^{2}-\mathbf {\color {red}a} \cdot \mathbf {\color {blue}b} -\mathbf {\color {red}a} \cdot \mathbf {\color {blue}b} +{\color {blue}b}^{2}\\&={\color {red}a}^{2}-2\mathbf {\color {red}a} \cdot \mathbf {\color {blue}b} +{\color {blue}b}^{2}\\{\color {orange}c}^{2}&={\color {red}a}^{2}+{\color {blue}b}^{2}-2{\color {red}a}{\color {blue}b}\cos \mathbf {\color {purple}\theta } \\\end{aligned}}}$$

cual es la ley de los cosenos .

Hay dos operaciones ternarias que involucran el producto escalar y el producto vectorial .

El triple producto escalar de tres vectores se define como Su valor es el determinante de la matriz cuyas columnas son las coordenadas cartesianas de los tres vectores. Es el volumen con signo del paralelepípedo definido por los tres vectores, y es isomorfo al caso especial tridimensional del producto exterior de tres vectores.$${\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ).}$$

El producto triple vectorial se define por ^{[2] [3]} Esta identidad, también conocida como fórmula de Lagrange , puede recordarse como "ACB menos ABC", teniendo en cuenta qué vectores están unidos por puntos. Esta fórmula tiene aplicaciones para simplificar los cálculos vectoriales en física .$${\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=(\mathbf {a} \cdot \mathbf {c} )\,\mathbf {b} -(\mathbf {a} \cdot \mathbf {b} )\,\mathbf {c} .}$$

En física , el producto escalar toma dos vectores y devuelve una cantidad escalar . También se lo conoce como "producto escalar". El producto escalar de dos vectores se puede definir como el producto de las magnitudes de los dos vectores y el coseno del ángulo entre los dos vectores. Por lo tanto, de manera alternativa, se define como el producto de la proyección del primer vector sobre el segundo vector y la magnitud del segundo vector.$${\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} |\,|\mathbf {b} |\cos \theta }$$

Por ejemplo: ^{[10] [11]}

• El trabajo mecánico es el producto escalar de los vectores de fuerza y ​​desplazamiento ,
• La potencia es el producto escalar de la fuerza y ​​la velocidad .

Para vectores con elementos complejos , el uso de la definición dada del producto escalar conduciría a propiedades bastante diferentes. Por ejemplo, el producto escalar de un vector consigo mismo podría ser cero sin que el vector sea el vector cero (por ejemplo, esto sucedería con el vector ). Esto a su vez tendría consecuencias para nociones como longitud y ángulo. Propiedades como la norma definida positiva se pueden salvar a costa de renunciar a las propiedades simétricas y bilineales del producto escalar, a través de la definición alternativa ^{[12] [2]} donde es el conjugado complejo de . Cuando los vectores se representan por vectores columna , el producto escalar se puede expresar como un producto matricial que involucra una transpuesta conjugada , denotada con el superíndice H:${\displaystyle \mathbf {a} =[1\ i]}$$${\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i}{{a_{i}}\,{\overline {b_{i}}}},}$$${\displaystyle {\overline {b_{i}}}}$${\displaystyle b_{i}}$

$${\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} ^{\mathsf {H}}\mathbf {a} .}$$

En el caso de vectores con componentes reales, esta definición es la misma que en el caso real. El producto escalar de cualquier vector consigo mismo es un número real no negativo, y es distinto de cero excepto para el vector cero. Sin embargo, el producto escalar complejo es sesquilineal en lugar de bilineal, ya que es lineal conjugado y no lineal en . El producto escalar no es simétrico, ya que El ángulo entre dos vectores complejos viene dado por${\displaystyle \mathbf {a} }$$${\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}.}$$$${\displaystyle \cos \theta ={\frac {\operatorname {Re} (\mathbf {a} \cdot \mathbf {b} )}{\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|}}.}$$

El producto escalar complejo conduce a las nociones de formas hermíticas y espacios de productos internos generales , que se utilizan ampliamente en matemáticas y física .

El producto escalar propio de un vector complejo , que involucra la transpuesta conjugada de un vector fila, también se conoce como norma al cuadrado , , en honor a la norma euclidiana ; es una generalización vectorial del cuadrado absoluto de un escalar complejo (ver también: distancia euclidiana al cuadrado ).${\displaystyle \mathbf {a} \cdot \mathbf {a} =\mathbf {a} ^{\mathsf {H}}\mathbf {a} }$${\textstyle \mathbf {a} \cdot \mathbf {a} =\|\mathbf {a} \|^{2}}$

El producto interno generaliza el producto escalar a espacios vectoriales abstractos sobre un cuerpo de escalares , ya sea el cuerpo de números reales o el cuerpo de números complejos . Generalmente se denota mediante corchetes angulares .${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$${\displaystyle \left\langle \mathbf {a} \,,\mathbf {b} \right\rangle }$

El producto interno de dos vectores sobre el cuerpo de números complejos es, en general, un número complejo y es sesquilineal en lugar de bilineal. Un espacio de producto interno es un espacio vectorial normado y el producto interno de un vector consigo mismo es real y positivo-definido.

El producto escalar se define para vectores que tienen un número finito de elementos . Por lo tanto, estos vectores pueden considerarse funciones discretas : un vector de longitud es, entonces, una función con dominio y es una notación para la imagen de por la función/vector .${\displaystyle n}$${\displaystyle u}$ ${\displaystyle \{k\in \mathbb {N} :1\leq k\leq n\}}$${\displaystyle u_{i}}$${\displaystyle i}$${\displaystyle u}$

Esta noción se puede generalizar a funciones continuas : así como el producto interno de los vectores utiliza una suma sobre los componentes correspondientes, el producto interno de las funciones se define como una integral sobre algún intervalo [ a ,  b ] : ^[2]

$${\displaystyle \left\langle u,v\right\rangle =\int _{a}^{b}u(x)v(x)\,dx.}$$

Generalizado aún más a funciones complejas y , por analogía con el producto interno complejo anterior, da ^[2]${\displaystyle \psi (x)}$${\displaystyle \chi (x)}$

$${\displaystyle \left\langle \psi ,\chi \right\rangle =\int _{a}^{b}\psi (x){\overline {\chi (x)}}\,dx.}$$

Los productos internos pueden tener una función de ponderación (es decir, una función que pondera cada término del producto interno con un valor). Explícitamente, el producto interno de las funciones y con respecto a la función de ponderación es${\displaystyle u(x)}$${\displaystyle v(x)}$${\displaystyle r(x)>0}$

$${\displaystyle \left\langle u,v\right\rangle _{r}=\int _{a}^{b}r(x)u(x)v(x)\,dx.}$$

Un producto escalar doble para matrices es el producto interno de Frobenius , que es análogo al producto escalar de vectores. Se define como la suma de los productos de los componentes correspondientes de dos matrices y del mismo tamaño:${\displaystyle \mathbf {A} }$${\displaystyle \mathbf {B} }$

$${\displaystyle \mathbf {A} :\mathbf {B} =\sum _{i}\sum _{j}A_{ij}{\overline {B_{ij}}}=\operatorname {tr} (\mathbf {B} ^{\mathsf {H}}\mathbf {A} )=\operatorname {tr} (\mathbf {A} \mathbf {B} ^{\mathsf {H}}).}$$Y para matrices reales,$${\displaystyle \mathbf {A} :\mathbf {B} =\sum _{i}\sum _{j}A_{ij}B_{ij}=\operatorname {tr} (\mathbf {B} ^{\mathsf {T}}\mathbf {A} )=\operatorname {tr} (\mathbf {A} \mathbf {B} ^{\mathsf {T}})=\operatorname {tr} (\mathbf {A} ^{\mathsf {T}}\mathbf {B} )=\operatorname {tr} (\mathbf {B} \mathbf {A} ^{\mathsf {T}}).}$$

Al escribir una matriz como diádica , podemos definir un producto de doble punto diferente (ver Diádicas § Producto de diádica y diádica ) sin embargo no es un producto interno.

El producto interno entre un tensor de orden y un tensor de orden es un tensor de orden , consulte Contracción del tensor para obtener más detalles.${\displaystyle n}$${\displaystyle m}$${\displaystyle n+m-2}$

El algoritmo sencillo para calcular un producto escalar de punto flotante de vectores puede sufrir una cancelación catastrófica . Para evitarlo, se utilizan enfoques como el algoritmo de suma de Kahan .

Una función de producto escalar se incluye en:

• BLAS nivel 1 real SDOT, DDOT; complejo CDOTU, ZDOTU = X^T * Y, CDOTC,ZDOTC = X^H * Y
• Fortran como dot_product(A,B)osum(conjg(A) * B)
• Julia como   A' * Bo biblioteca estándar de Álgebra lineal comodot(A, B)
• R (lenguaje de programación) como sum(A * B)para vectores o, más generalmente para matrices, comoA %*% B
• Matlab como   A' * B  o   conj(transpose(A)) * B  o   sum(conj(A) .* B)  o  dot(A, B)
• Python (paquete NumPy ) como   np.matmul(A, B)  o   np.dot(A, B)  o  np.inner(A, B)
• GNU Octave como   sum(conj(X) .* Y, dim), y código similar como Matlab
• Biblioteca de núcleo matemático Intel oneAPI p?dot real dot = sub(x)'*sub(y); p?dotc complejodotc = conjg(sub(x)')*sub(y)

Wikimedia Commons tiene medios relacionados con Producto escalar .

• "Producto interno", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Explicación del producto escalar incluso con vectores complejos
• "Producto punto" de Bruce Torrence, Wolfram Demonstrations Project , 2007.