Proceso de jerarquía analítica
Es posible que este artículo contenga investigaciones originales . ( Julio de 2017 ) |

En la teoría de la toma de decisiones , el proceso analítico jerárquico ( AHP ), también proceso analítico jerárquico , [1] es una técnica estructurada para organizar y analizar decisiones complejas , basada en las matemáticas y la psicología . Fue desarrollado por Thomas L. Saaty en la década de 1970; Saaty se asoció con Ernest Forman para desarrollar el software Expert Choice en 1983, y AHP ha sido ampliamente estudiado y refinado desde entonces. Representa un enfoque preciso para cuantificar los pesos de los criterios de decisión. Las experiencias de los expertos individuales se utilizan para estimar las magnitudes relativas de los factores a través de comparaciones por pares. Cada uno de los encuestados compara la importancia relativa de cada par de elementos utilizando un cuestionario especialmente diseñado. La importancia relativa de los criterios se puede determinar con la ayuda del AHP comparando los criterios y, si corresponde, los subcriterios en pares por expertos o tomadores de decisiones. Sobre esta base, se puede encontrar la mejor alternativa. [2]
Usos y aplicaciones
El AHP está orientado a la toma de decisiones grupales , [3] y se utiliza para situaciones de decisión en campos como el gobierno, los negocios, la industria, [4] la atención médica y la educación.
En lugar de prescribir una decisión "correcta", el AHP ayuda a los encargados de tomar decisiones a encontrar la que mejor se adapta a su objetivo y a su comprensión del problema. Proporciona un marco integral y racional para estructurar un problema de decisión, para representar y cuantificar sus elementos, para relacionar esos elementos con los objetivos generales y para evaluar soluciones alternativas.
Los usuarios del AHP primero descomponen su problema de decisión en una jerarquía de subproblemas más fáciles de comprender, cada uno de los cuales puede analizarse de forma independiente. Los elementos de la jerarquía pueden relacionarse con cualquier aspecto del problema de decisión (tangible o intangible, medido cuidadosamente o estimado de manera aproximada, bien o mal comprendido), cualquier cosa que se aplique a la decisión en cuestión.
Una vez construida la jerarquía, los encargados de la toma de decisiones evalúan sus diversos elementos comparándolos entre sí de dos en dos, en relación con su impacto sobre un elemento superior en la jerarquía. Al hacer las comparaciones, los encargados de la toma de decisiones pueden utilizar datos concretos sobre los elementos, y también pueden utilizar sus juicios sobre el significado y la importancia relativos de los elementos. Para realizar las evaluaciones se pueden utilizar los juicios humanos, y no sólo la información subyacente. [5]
El AHP convierte estas evaluaciones en valores numéricos que pueden procesarse y compararse en todo el espectro del problema. Se deriva un peso numérico o prioridad para cada elemento de la jerarquía, lo que permite comparar elementos diversos y a menudo inconmensurables entre sí de una manera racional y coherente. Esta capacidad distingue al AHP de otras técnicas de toma de decisiones.
En el paso final del proceso, se calculan las prioridades numéricas para cada una de las alternativas de decisión. Estos números representan la capacidad relativa de las alternativas para lograr el objetivo de la decisión, por lo que permiten una consideración sencilla de los distintos cursos de acción.
Si bien puede ser utilizado por personas que trabajan en decisiones sencillas, el Proceso Analítico Jerárquico (AHP) es más útil cuando equipos de personas trabajan en problemas complejos, especialmente aquellos con grandes riesgos, que involucran percepciones y juicios humanos, cuyas resoluciones tienen repercusiones a largo plazo. [6]
Las situaciones de decisión a las que se puede aplicar el AHP incluyen: [1]
- Elección: La selección de una alternativa de un conjunto dado de alternativas, generalmente cuando hay múltiples criterios de decisión involucrados.
- Clasificación : Poner un conjunto de alternativas en orden desde la más deseable a la menos deseable.
- Priorización: determinar el mérito relativo de los miembros de un conjunto de alternativas, en lugar de seleccionar uno solo o simplemente clasificarlos.
- Asignación de recursos : distribución de recursos entre un conjunto de alternativas
- Benchmarking : comparación de los procesos de la propia organización con los de otras organizaciones de primera línea
- Gestión de la calidad : cómo abordar los aspectos multidimensionales de la calidad y la mejora de la calidad
- Resolución de conflictos : solución de disputas entre partes con objetivos o posiciones aparentemente incompatibles [3]
Las aplicaciones de AHP incluyen la planificación , la asignación de recursos , el establecimiento de prioridades y la selección entre alternativas. [6] Otras áreas han incluido la previsión , la gestión de calidad total , la reingeniería de procesos de negocios , el despliegue de funciones de calidad y el cuadro de mando integral . [1] Otros usos de AHP se discuten en la literatura:
- Decidir cuál es la mejor manera de reducir el impacto del cambio climático global ( Fondazione Eni Enrico Mattei ) [7]
- Cuantificación de la calidad global de los sistemas de software ( Microsoft Corporation ) [8]
- Selección de profesores universitarios ( Universidad Bloomsburg de Pensilvania ) [9]
- Decidir dónde ubicar plantas de fabricación en el extranjero ( Universidad de Cambridge ) [10]
- Evaluación de riesgos en la operación de oleoductos transnacionales ( Sociedad Estadounidense de Ingenieros Civiles ) [11]
- Decidir cuál es la mejor manera de gestionar las cuencas hidrográficas de EE. UU. ( Departamento de Agricultura de EE. UU. ) [12]
- Definir y evaluar de forma más eficaz los enfoques de implementación de SAP (expertos de SAP)
- Evaluación integrada de la sostenibilidad de una comunidad en términos de medio ambiente, economía, sociedad, institución y cultura. [13]
- Herramienta de toma de decisiones para la construcción acelerada de puentes que ayuda a determinar la viabilidad de la construcción acelerada de puentes (ABC) en comparación con los métodos de construcción tradicionales y a seleccionar estrategias de construcción y contratación adecuadas caso por caso. [14]
El AHP se utiliza a veces para diseñar procedimientos muy específicos para situaciones particulares, como la clasificación de edificios según su importancia histórica. [15] Recientemente se aplicó a un proyecto que utiliza imágenes de vídeo para evaluar el estado de las carreteras en Virginia . Los ingenieros de carreteras lo utilizaron primero para determinar el alcance óptimo del proyecto y luego para justificar su presupuesto ante los legisladores . [16]
Los pesos de la matriz de juicio AHP pueden corregirse con los calculados mediante el método de la entropía. Esta variante del método AHP se denomina AHP-EM. [13] [17]
Educación e investigación académica
Aunque el uso del proceso de jerarquía analítica no requiere una formación académica especializada, se considera un tema importante en muchas instituciones de educación superior, incluidas las escuelas de ingeniería [18] y las escuelas de posgrado de negocios . [19] Es un tema particularmente importante en el campo de la calidad y se enseña en muchos cursos especializados, incluidos Six Sigma , Lean Six Sigma y QFD . [20] [21] [22]
El Simposio Internacional sobre el Proceso de Jerarquía Analítica (ISAHP) celebra reuniones bienales de académicos y profesionales interesados en el campo. Se cubre una amplia gama de temas. Los de 2005 iban desde "Establecimiento de estándares de pago para especialistas quirúrgicos", hasta "Hoja de ruta tecnológica estratégica", hasta "Reconstrucción de infraestructura en países devastados". [23] En la reunión de 2007 en Valparaíso, Chile , se presentaron 90 trabajos de 19 países, incluidos los EE. UU., Alemania, Japón, Chile, Malasia y Nepal. [24] Se presentó un número similar de trabajos en el simposio de 2009 en Pittsburgh, Pensilvania , cuando estuvieron representados 28 países. [25] Los temas de los trabajos incluyeron Estabilización económica en Letonia , Selección de cartera en el sector bancario , Gestión de incendios forestales para ayudar a mitigar el calentamiento global y Microproyectos rurales en Nepal .
Usar

Como se puede ver en el material que sigue, el uso del AHP implica la síntesis matemática de numerosos juicios sobre el problema de decisión en cuestión. No es raro que estos juicios se cuenten por docenas o incluso por cientos. Si bien los cálculos se pueden hacer a mano o con una calculadora, es mucho más común utilizar uno de los diversos métodos informáticos para ingresar y sintetizar los juicios. El más simple de ellos implica un software de hoja de cálculo estándar, mientras que los más complejos utilizan software personalizado, a menudo mejorado con dispositivos especiales para adquirir los juicios de los tomadores de decisiones reunidos en una sala de reuniones.
El procedimiento para utilizar el AHP se puede resumir de la siguiente manera:
- Modele el problema como una jerarquía que contenga el objetivo de decisión, las alternativas para alcanzarlo y los criterios para evaluar las alternativas.
- Establezca prioridades entre los elementos de la jerarquía mediante una serie de juicios basados en comparaciones de pares de elementos. Por ejemplo, al comparar posibles compras de bienes raíces comerciales, los inversores podrían decir que prefieren la ubicación al precio y el precio al momento.
- Sintetice estos juicios para obtener un conjunto de prioridades generales para la jerarquía. Esto combinaría los juicios de los inversores sobre la ubicación, el precio y el momento de la compra de las propiedades A, B, C y D en prioridades generales para cada propiedad.
- Comprobar la consistencia de las sentencias.
- Llegar a una decisión final basada en los resultados de este proceso. [26]
Estos pasos se describen con más detalle a continuación.
Modelar el problema como una jerarquía
El primer paso en el proceso de análisis jerárquico es modelar el problema como una jerarquía. Para ello, los participantes exploran los aspectos del problema en niveles que van desde lo general hasta lo detallado, y luego lo expresan en la forma multinivel que requiere el PAH. A medida que trabajan para construir la jerarquía, aumentan su comprensión del problema, de su contexto y de los pensamientos y sentimientos de los demás sobre ambos. [26]
Jerarquías definidas
Una jerarquía es un sistema estratificado de clasificación y organización de personas, cosas, ideas, etc., en el que cada elemento del sistema, excepto el superior, está subordinado a uno o más elementos. Aunque el concepto de jerarquía se comprende fácilmente de manera intuitiva, también se puede describir matemáticamente. [27] Los diagramas de jerarquías suelen tener una forma similar a la de las pirámides, pero, salvo por el hecho de tener un único elemento en la cima, no hay nada necesariamente piramidal en una jerarquía.
Las organizaciones humanas suelen estructurarse como jerarquías, en las que el sistema jerárquico se utiliza para asignar responsabilidades, ejercer el liderazgo y facilitar la comunicación. Las jerarquías habituales de "cosas" incluyen la unidad de torre de una computadora de escritorio en la "parte superior", con su monitor, teclado y mouse subordinados "debajo".
En el mundo de las ideas, utilizamos jerarquías para ayudarnos a adquirir un conocimiento detallado de la realidad compleja: estructuramos la realidad en sus partes constituyentes, y estas a su vez en sus propias partes constituyentes, descendiendo por la jerarquía tantos niveles como queramos. En cada paso, nos centramos en comprender un solo componente del todo, ignorando temporalmente los demás componentes en este y todos los demás niveles. A medida que avanzamos en este proceso, aumentamos nuestra comprensión global de cualquier realidad compleja que estemos estudiando.
Pensemos en la jerarquía que utilizan los estudiantes de medicina mientras aprenden anatomía: consideran por separado el sistema musculoesquelético (incluidas las partes y subpartes, como la mano y los músculos y huesos que lo componen), el sistema circulatorio (y sus muchos niveles y ramas), el sistema nervioso (y sus numerosos componentes y subsistemas), etc., hasta que han cubierto todos los sistemas y las subdivisiones importantes de cada uno. Los estudiantes avanzados continúan con la subdivisión hasta el nivel de la célula o la molécula. Al final, los estudiantes comprenden el "panorama general" y una cantidad considerable de sus detalles. No solo eso, sino que comprenden la relación de las partes individuales con el todo. Al trabajar jerárquicamente, han adquirido una comprensión integral de la anatomía.
De manera similar, cuando abordamos un problema de decisión complejo, podemos utilizar una jerarquía para integrar grandes cantidades de información en nuestra comprensión de la situación. A medida que construimos esta estructura de información, formamos una imagen cada vez mejor del problema en su conjunto. [26]
Jerarquías en el AHP
Una jerarquía AHP es un medio estructurado para modelar la decisión en cuestión. Consiste en un objetivo general, un grupo de opciones o alternativas para alcanzar el objetivo y un grupo de factores o criterios que relacionan las alternativas con el objetivo. Los criterios se pueden desglosar en subcriterios, sub-subcriterios, etc., en tantos niveles como requiera el problema. Un criterio puede no aplicarse de manera uniforme, sino que puede tener diferencias graduadas como un poco de dulzura es agradable pero demasiada dulzura puede ser dañina. En ese caso, el criterio se divide en subcriterios que indican diferentes intensidades del criterio, como: poco, medio, alto y estas intensidades se priorizan a través de comparaciones bajo el criterio principal, dulzura. Las descripciones publicadas de aplicaciones AHP a menudo incluyen diagramas y descripciones de sus jerarquías; algunas simples se muestran a lo largo de este artículo. Se han recopilado y reimpreso jerarquías AHP más complejas en al menos un libro. [28] Se pueden encontrar jerarquías más complejas en una página de discusión especial para este artículo .
El diseño de cualquier jerarquía AHP dependerá no sólo de la naturaleza del problema en cuestión, sino también de los conocimientos, juicios, valores, opiniones, necesidades, deseos, etc. de los participantes en el proceso de toma de decisiones. La construcción de una jerarquía normalmente implica un debate, una investigación y un descubrimiento importantes por parte de los implicados. Incluso después de su construcción inicial, se puede cambiar para dar cabida a criterios nuevos o a criterios que originalmente no se consideraban importantes; también se pueden añadir, eliminar o cambiar alternativas. [26]
Para comprender mejor las jerarquías AHP, considere un problema de decisión con un objetivo a alcanzar, tres formas alternativas de alcanzar el objetivo y cuatro criterios con respecto a los cuales se deben medir las alternativas.
Esta jerarquía se puede visualizar como un diagrama como el que se muestra inmediatamente debajo, con el objetivo en la parte superior, las tres alternativas en la parte inferior y los cuatro criterios en el medio. Hay términos útiles para describir las partes de estos diagramas: cada caja se llama nodo. Un nodo que está conectado a uno o más nodos en un nivel inferior se llama nodo padre. Los nodos a los que está conectado de esta manera se llaman sus hijos.
Aplicando estas definiciones al diagrama que aparece a continuación, el objetivo es el padre de los cuatro criterios, y los cuatro criterios son hijos del objetivo. Cada criterio es un padre de las tres alternativas. Observe que solo hay tres alternativas, pero en el diagrama, cada una de ellas se repite bajo cada uno de sus padres.

Para reducir el tamaño del dibujo requerido, es común representar las jerarquías AHP como se muestra en el diagrama siguiente, con un solo nodo para cada alternativa y con múltiples líneas que conectan las alternativas y los criterios que se aplican a ellas. Para evitar el desorden, a veces se omiten estas líneas o se reduce su número. Independientemente de cualquier simplificación de este tipo en el diagrama, en la jerarquía real cada criterio está conectado individualmente a las alternativas. Se puede pensar que las líneas se dirigen hacia abajo desde el padre en un nivel a sus hijos en el nivel inferior.
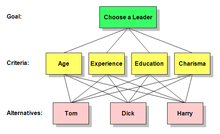
Evaluar la jerarquía
Una vez construida la jerarquía, los participantes la analizan mediante una serie de comparaciones por pares que derivan escalas numéricas de medición para los nodos. Los criterios se comparan por pares con el objetivo de importancia. Las alternativas se comparan por pares con cada uno de los criterios de preferencia. Las comparaciones se procesan matemáticamente y se derivan prioridades para cada nodo.
Consideremos el ejemplo de "Elegir un líder" que se muestra más arriba. Una tarea importante de los encargados de tomar decisiones es determinar el peso que se le dará a cada criterio para elegir un líder. Otra tarea importante es determinar el peso que se le dará a cada candidato con respecto a cada uno de los criterios. El AHP no sólo les permite hacer eso, sino que también les permite asignar un valor numérico significativo y objetivo a cada uno de los cuatro criterios.
A diferencia de la mayoría de las encuestas que adoptan la escala Likert de cinco puntos , el cuestionario de AHP es de 9 a 1 a 9. [29]
Establecer prioridades
Esta sección explica las prioridades, muestra cómo se establecen y proporciona un ejemplo sencillo.
Prioridades definidas y explicadas
Las prioridades son números asociados a los nodos de una jerarquía AHP. Representan los pesos relativos de los nodos en cualquier grupo.
Al igual que las probabilidades, las prioridades son números absolutos entre cero y uno, sin unidades ni dimensiones. Un nodo con prioridad .200 tiene el doble de peso para alcanzar la meta que uno con prioridad .100, diez veces más peso que uno con prioridad .020, y así sucesivamente. Según el problema en cuestión, el "peso" puede referirse a la importancia, la preferencia, la probabilidad o cualquier factor que estén considerando los que toman las decisiones.
Las prioridades se distribuyen en una jerarquía según su arquitectura y sus valores dependen de la información ingresada por los usuarios del proceso. Las prioridades de la Meta, los Criterios y las Alternativas están íntimamente relacionadas, pero deben considerarse por separado.
Por definición, la prioridad del Objetivo es 1.000. Las prioridades de las alternativas siempre suman 1.000. Las cosas se pueden complicar con múltiples niveles de Criterios, pero si solo hay un nivel, sus prioridades también suman 1.000. Todo esto se ilustra con las prioridades en el siguiente ejemplo.

Observe que las prioridades en cada nivel del ejemplo (el objetivo, los criterios y las alternativas) suman 1.000.
Las prioridades que se muestran son las que existían antes de que se ingresara información sobre los pesos de los criterios o alternativas, por lo que las prioridades dentro de cada nivel son todas iguales. Se denominan prioridades predeterminadas de la jerarquía. Si se agregara un quinto criterio a esta jerarquía, la prioridad predeterminada para cada criterio sería 0,200. Si solo hubiera dos alternativas, cada una tendría una prioridad predeterminada de 0,500.
Se aplican dos conceptos adicionales cuando una jerarquía tiene más de un nivel de criterios: prioridades locales y prioridades globales. Considere la jerarquía que se muestra a continuación, que tiene varios subcriterios bajo cada criterio.
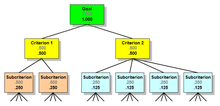
Las prioridades locales, que se muestran en gris, representan los pesos relativos de los nodos dentro de un grupo de hermanos con respecto a su padre. Las prioridades locales de cada grupo de Criterios y sus Subcriterios hermanos suman 1.000. Las prioridades globales, que se muestran en negro, se obtienen multiplicando las prioridades locales de los hermanos por la prioridad global de su padre. Las prioridades globales para todos los subcriterios en el nivel suman 1.000.
La regla es la siguiente: dentro de una jerarquía, las prioridades globales de los nodos secundarios siempre suman la prioridad global de su padre. Dentro de un grupo de secundarios, las prioridades locales suman 1.000.
Hasta ahora, solo hemos analizado las prioridades predeterminadas. A medida que avanza el proceso de jerarquía analítica, las prioridades cambiarán respecto de sus valores predeterminados a medida que los encargados de tomar decisiones ingresen información sobre la importancia de los distintos nodos. Para ello, realizan una serie de comparaciones por pares.
Ejemplos prácticos
Los profesionales con experiencia saben que la mejor manera de comprender el AHP es trabajar con casos y ejemplos. Se incluyen como apéndices de este artículo dos estudios de casos detallados , diseñados específicamente como ejemplos de enseñanza en profundidad:
- Ejemplo sencillo paso a paso con cuatro criterios y tres alternativas: Cómo elegir un líder para una organización .
- Ejemplo más complejo paso a paso con diez criterios/subcriterios y seis alternativas: compra de un automóvil familiar y ejemplo de selección de maquinaria. [30]
Algunos de los libros sobre AHP contienen ejemplos prácticos de su uso, aunque no suelen estar pensados para ser ayudas de aprendizaje paso a paso. [26] [31] Uno de ellos contiene un puñado de ejemplos ampliados, además de unas 400 jerarquías de AHP descritas brevemente e ilustradas con figuras. [28] Se analizan muchos ejemplos, principalmente para audiencias profesionales, en artículos publicados por el Simposio Internacional sobre el Proceso Analítico Jerárquico . [32] [33] [34] [35] [36]
Críticas
El AHP está incluido en la mayoría de los libros de texto de investigación de operaciones y ciencias de la gestión , y se enseña en numerosas universidades; se utiliza ampliamente en organizaciones que han investigado cuidadosamente sus fundamentos teóricos. [1] El método tiene sus críticos. [8] A principios de la década de 1990, se publicó una serie de debates entre críticos y defensores del AHP en Management Science [37] [38] [39] [40] y The Journal of the Operational Research Society, [41] [42] [43] dos prestigiosas revistas en las que Saaty y sus colegas tuvieron una influencia considerable. Estos debates parecen haberse resuelto a favor del AHP:
- En 2001 se publicó un artículo detallado en Operations Research .
- Un artículo de Management Science de 2008 que analiza 15 años de progreso en todas las áreas de la toma de decisiones multicriterio
- En 2008, la principal sociedad de investigación de operaciones, el Instituto de Investigación de Operaciones y Ciencias de la Gestión, reconoció formalmente el amplio impacto de AHP en sus campos. [44]
Un artículo de 1997 examinó posibles fallas en la escala verbal (en comparación con la numérica) que se usa a menudo en las comparaciones por pares del AHP. [45] Otro artículo del mismo año afirmó que cambios inocuos al modelo AHP pueden introducir orden donde no existe tal orden. [46] Un artículo de 2006 concluyó que la adición de criterios para los cuales todas las alternativas funcionan por igual puede alterar las prioridades de las alternativas. [47]
En 2021 se publicó la primera evaluación integral del AHP en un libro escrito por dos académicos de la Universidad Politécnica de Valencia y la Universidad Politécnica de Cartagena , y publicado por Springer Nature . Basado en una investigación empírica y testimonios objetivos de 101 investigadores, el estudio encontró al menos 30 fallas en el AHP y lo encontró inadecuado para problemas complejos y, en ciertas situaciones, incluso para problemas pequeños. [48]
Inversión de rango
La toma de decisiones implica clasificar las alternativas en función de criterios o atributos de esas alternativas. Un axioma de algunas teorías de la toma de decisiones es que cuando se añaden nuevas alternativas a un problema de decisión, la clasificación de las alternativas anteriores no debe cambiar, es decir, no debe producirse una " inversión de la clasificación ".
Existen dos escuelas de pensamiento sobre la inversión de rangos. Una sostiene que las nuevas alternativas que no introducen atributos adicionales no deberían causar una inversión de rangos bajo ninguna circunstancia. La otra sostiene que hay algunas situaciones en las que se puede esperar razonablemente una inversión de rangos. La formulación original del AHP permitía inversiones de rangos. En 1993, Forman [49] introdujo un segundo modo de síntesis del AHP, llamado modo de síntesis ideal, para abordar situaciones de elección en las que la adición o eliminación de una alternativa "irrelevante" no debería causar ni causará un cambio en los rangos de las alternativas existentes. La versión actual del AHP puede dar cabida a ambas escuelas: su modo ideal preserva el rango, mientras que su modo distributivo permite que los rangos cambien. Cualquiera de los dos modos se selecciona de acuerdo con el problema en cuestión.
La inversión de rango y el AHP se analizan en profundidad en un artículo de 2001 en Operations Research [1], así como en un capítulo titulado Rank Preservation and Reversal [Preservación y inversión de rango ], en el libro básico actual sobre AHP. [31] Este último presenta ejemplos publicados de inversión de rango debido a la adición de copias y copias cercanas de una alternativa, debido a la intransitividad de las reglas de decisión, debido a la adición de alternativas fantasma y señuelo, y debido al fenómeno de conmutación en las funciones de utilidad. También analiza los modos distributivo e ideal del AHP.
En 2014 se encontró una nueva forma de inversión de rango de AHP [50] en la que AHP produce una inversión del orden de rango al eliminar datos irrelevantes, es decir, datos que no diferencian alternativas.
Existen distintos tipos de inversiones de rango. Además, otros métodos además del AHP pueden presentar dichas inversiones de rango. En la página sobre inversiones de rango en la toma de decisiones se ofrece más información sobre las inversiones de rango con el AHP y otros métodos MCDM .
No monotonía de algunos métodos de extracción de peso
Dentro de una matriz de comparación, se puede reemplazar un juicio por un juicio menos favorable y luego verificar si la indicación de la nueva prioridad se vuelve menos favorable que la prioridad original. En el contexto de las matrices de torneo, Oskar Perron [51] ha demostrado que el método del vector propio derecho principal no es monótono. Este comportamiento también se puede demostrar para matrices recíprocas nxn, donde n > 3. Se discuten enfoques alternativos en otros lugares. [52] [53] [54] [55]
Véase también
- Proceso de jerarquía analítica: ejemplo de un automóvil
- Proceso de jerarquía analítica: ejemplo de líder
- Proceso analítico de red
- Teorema de imposibilidad de Arrow
- Toma de decisiones
- Paradoja de la toma de decisiones
- Software de toma de decisiones
- Proceso de decisión jerárquico
- Por L. L. Thurstone
- Ley del juicio comparativo
- Análisis de decisiones multicriterio
- Comparación por pares
- Preferencia
- Análisis de componentes principales
- Inversiones de rango en la toma de decisiones
Referencias
- ^ abcde Forman, Ernest H.; Saul I. Gass (julio de 2001). "El proceso de jerarquía analítica: una exposición". Investigación de operaciones . 49 (4): 469–487. doi :10.1287/opre.49.4.469.11231.
- ^ Fabianek, Paul; Christian Will; Stefanie Wolff; Reinhard Madlener (2020). "¿Verde y regional? Un marco de evaluación de criterios múltiples para el suministro de electricidad verde para vehículos eléctricos en Alemania". Transportation Research Part D . 87 (D): 102504. doi :10.1016/j.trd.2020.102504.
- ^ ab Saaty, Thomas L.; Peniwati, Kirti (2008). Toma de decisiones grupal: identificar y reconciliar diferencias . Pittsburgh, Pensilvania: RWS Publications. ISBN 978-1-888603-08-8.
- ^ Saracoglu, BO (2013). "Selección de ubicaciones de inversión industrial en planes maestros de países". Revista Europea de Ingeniería Industrial . 7 (4): 416–441. doi :10.1504/EJIE.2013.055016.
- ^ Saaty, Thomas L. (junio de 2008). "Medición relativa y su generalización en la toma de decisiones: por qué las comparaciones por pares son fundamentales en matemáticas para la medición de factores intangibles: el proceso analítico de jerarquía/red" (PDF) . Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales, Serie A: Matemáticas . 102 (2): 251–318. CiteSeerX 10.1.1.455.3274 . doi :10.1007/bf03191825. S2CID 42215574 . Consultado el 22 de diciembre de 2008 .
- ^ ab Bhushan, Navneet; Kanwal Rai (enero de 2004). Toma de decisiones estratégicas: aplicación del proceso analítico jerárquico. Londres: Springer-Verlag. ISBN 978-1-85233-756-8.
- ^ Berrittella, M.; A. Certa; M. Enea; P. Zito (enero de 2007). "Un proceso analítico jerárquico para la evaluación de políticas de transporte para reducir los impactos del cambio climático" (PDF) . Fondazione Eni Enrico Mattei (Milán). Archivado desde el original (PDF) el 4 de marzo de 2016. Consultado el 16 de febrero de 2011 .
- ^ ab McCaffrey, James (junio de 2005). "Ejecución de pruebas: el proceso de jerarquía analítica". Revista MSDN . Consultado el 21 de agosto de 2007 .
- ^ Grandzol, John Richard (agosto de 2005). "Mejora del proceso de selección de profesores en la educación superior: un caso a favor del proceso de jerarquía analítica" (PDF) . Aplicaciones de las relaciones internacionales . 6 . Archivado desde el original (PDF) el 2007-10-30 . Consultado el 2007-08-21 .
- ^ Atthirawong, Walailak; Bart McCarthy (septiembre de 2002). "Una aplicación del proceso de jerarquía analítica a la toma de decisiones sobre ubicación internacional". En Gregory, Mike (ed.). Actas del 7.º Simposio Anual Internacional de Manufactura de Cambridge: Reestructuración de la Manufactura Global . Cambridge, Inglaterra: Universidad de Cambridge. págs. 1–18. Archivado desde el original (PDF) el 22 de marzo de 2016. Consultado el 23 de octubre de 2007 .
- ^ Dey, Prasanta Kumar (noviembre de 2003). "El proceso de jerarquía analítica analiza el riesgo de operar oleoductos transnacionales en la India". Natural Hazards Review . 4 (4): 213–221. doi :10.1061/(ASCE)1527-6988(2003)4:4(213) . Consultado el 20 de agosto de 2007 .
- ^ de Steiguer, JE; Jennifer Duberstein; Vicente Lopes (octubre de 2003). "El proceso analítico jerárquico como medio para la gestión integrada de cuencas hidrográficas" (PDF) . En Renard, Kenneth G. (ed.). Primera conferencia interinstitucional sobre investigación de cuencas hidrográficas . Benson, Arizona: Departamento de Agricultura de los Estados Unidos, Servicio de Investigación Agrícola. pp. 736–740.
- ^ ab Wu, Guangdong; Duan, Kaifeng; Zuo, Jian; Zhao, Xianbo; Tang, Daizhong (13 de abril de 2017). "Evaluación integrada de la sostenibilidad de una comunidad de viviendas de alquiler público basada en un método híbrido de peso de entropía AHP y modelo de nube". Sustainability . 9 (4): 603. doi : 10.3390/su9040603 . ISSN 2071-1050. OCLC 7016685474.
- ^ Salem, O., Salman, B. y Ghorai, S. (2017). Aceleración de la construcción de puentes de carretera mediante técnicas y métodos de adquisición alternativos. Transporte, 33(2), 567-579. https://doi.org/10.3846/16484142.2017.1300942
- ^ Lippert, Barbara C.; Stephen F. Weber (octubre de 1995). "HIST 1.0; Software de soporte de decisiones para la clasificación de edificios por su importancia histórica" (PDF) . Instituto Nacional de Normas y Tecnología, NIST IR 5683. Consultado el 20 de agosto de 2007 .
- ^ Larson, Charles D.; Ernest H. Forman (enero de 2007). "Aplicación del proceso de jerarquía analítica para seleccionar el alcance del proyecto para la grabación en video y la recopilación de datos sobre el estado del pavimento". Compendio de artículos de la 86.ª reunión anual, CD-ROM . Junta de investigación sobre el transporte de las Academias Nacionales.
- ^ Duan, Ye; Mu, Hailin; Li, Nan; Li, Linlin; Xue, Zhaoquan (2016). "Investigación sobre la evaluación integral del nivel de desarrollo de la economía baja en carbono basada en el método de entropía AHP: un estudio de caso de Dalian". Energy Procedia . 104 : 468–474. doi : 10.1016/j.egypro.2016.12.079 .
- ^ Drake, PR (1998). "Uso del proceso analítico jerárquico en la enseñanza de la ingeniería" (PDF) . Revista internacional de enseñanza de la ingeniería . 14 (3): 191–196. Archivado desde el original (PDF) el 28 de noviembre de 2007 . Consultado el 20 de agosto de 2007 .
- ^ Bodin, Lawrence; Saul I. Gass (enero de 2004). "Ejercicios para enseñar el proceso analítico jerárquico". INFORMS Transactions on Education . 4 (2): 1–13. doi : 10.1287/ited.4.2.1 .
- ^ Hallowell, David L. (enero de 2005). "Proceso de jerarquía analítica (AHP): cómo orientarse". ISixSigma.com . Archivado desde el original el 11 de agosto de 2007. Consultado el 21 de agosto de 2007 .
- ^ "Proceso de jerarquía analítica (AHP)". QFD Institute . Archivado desde el original el 22 de agosto de 2007. Consultado el 21 de agosto de 2007 .
- ^ "Proceso de jerarquía analítica: descripción general". TheQualityPortal.com . Archivado desde el original el 29 de agosto de 2007. Consultado el 21 de agosto de 2007 .
- ^ "Nombres y documentos de los participantes, ISAHP 2005, Honolulu, Hawaii". Julio de 2005. Archivado desde el original el 29 de febrero de 2008. Consultado el 22 de agosto de 2007 .
- ^ Garuti, Claudio, ed. (2007). "Participant Names and Papers". Actas del 9º Simposio Internacional sobre el Proceso Analítico Jerárquico . Viña del Mar, Chile: ISAHP. Archivado desde el original el 2011-07-26 . Consultado el 2011-01-05 .
- ^ Saaty, Rozann, ed. (2009). "Nombres y artículos de los participantes". Actas del 10.º Simposio internacional sobre el proceso analítico de jerarquía/red . Pittsburgh, Pensilvania: ISAHP.
- ^ abcde Saaty, Thomas L. (2008). Toma de decisiones para líderes: el proceso analítico jerárquico para decisiones en un mundo complejo . Pittsburgh, Pensilvania: RWS Publications. ISBN 978-0-9620317-8-6.(Este libro es la fuente principal de las secciones en las que se cita).
- ^ Saaty, Thomas L. (2010). Principia Mathematica Decernendi: Principios matemáticos de la toma de decisiones . Pittsburgh, Pensilvania: RWS Publications. ISBN 978-1-888603-10-1.
- ^ ab Saaty, Thomas L. ; Ernest H. Forman (1992). El jerarca: un diccionario de jerarquías . Pittsburgh, Pensilvania: RWS Publications. ISBN 978-0-9620317-5-5.496 páginas, encuadernado en espiral. Cada entrada incluye una descripción y un diagrama de un modelo AHP; los modelos están agrupados en categorías: educativo, gobierno/política pública, gobierno público/estrategia, salud militar, sin fines de lucro, personal, planificación, político, etc.
- ^ Li, Rita Yi Man; Chau, Kwong Wing; Zeng, Frankie Fanjie (2019). "Ranking de riesgos para obras de construcción existentes y nuevas". Sustainability . 11 (10): 2863. doi : 10.3390/su11102863 .
- ^ Perez-Rodriguez, Fernando; Rojo-Alboreca, Alberto (2012-01-12). "Aplicación forestal del AHP mediante el uso del software MPC©". Forest Systems . 21 (3): 418–425. doi : 10.5424/fs/2012213-02641 . hdl : 10347/21679 .
- ^ ab Saaty, Thomas L. (2001). Fundamentos de la toma de decisiones y teoría de prioridades . Pittsburgh, Pensilvania: RWS Publications. ISBN 978-0-9620317-6-2.
- ^ "Actas del 6º Simposio Internacional sobre el AHP". Sitio web de la ISAHP . ISAHP. Agosto de 2001. Consultado el 3 de abril de 2009 .
- ^ "Actas del 7º Simposio Internacional sobre el AHP". Sitio web de la ISAHP . ISAHP. Agosto de 2003. Consultado el 3 de abril de 2009 .
- ^ "Actas del 8º Simposio Internacional sobre el AHP". Sitio web de la ISAHP . ISAHP. Agosto de 2005. Consultado el 3 de abril de 2009 .
- ^ "Actas del 9º Simposio Internacional sobre el AHP". Sitio web de la ISAHP . ISAHP. Agosto de 2007. Consultado el 3 de abril de 2009 .
- ^ "Actas del 10º Simposio Internacional sobre el AHP". Sitio web de la ISAHP . ISAHP. Agosto de 2009. Consultado el 5 de enero de 2011 .
- ^ Dyer, JS (1990): Observaciones sobre el proceso analítico jerárquico. En: Management Science, 36 (3), págs. 249-258.
- ^ MV Mikhalevic "Observaciones sobre la controversia Dyer-Saaty" Cybernetics and Systems Analysis, Volumen 30, Número 1 / Enero de 1994
- ^ Patrick T. Harker, Luis G. Vargas, "Respuesta a 'Observaciones sobre el proceso analítico jerárquico' de JS Dyer", Management Science, vol. 36, núm. 3 (marzo de 1990), págs. 269-273
- ^ Dyer, JS (1990b), "Una aclaración de 'Observaciones sobre el proceso de jerarquía analítica'", Management Science, Vol. 36 No.3, pp.274-5.
- ^ Holder, RD, Algunos comentarios sobre el proceso de jerarquía analítica, Journal of the Operational Research Society, 1990, 41, 11 1073-1076.
- ^ Thomas L. Saaty "Respuesta a los comentarios de Holder sobre el proceso de jerarquía analítica", The Journal of the Operational Research Society, vol. 42, n.º 10 (octubre de 1991), págs. 909-914
- ^ RD Holder "Respuesta a los comentarios de Holder sobre el proceso de jerarquía analítica: Respuesta a la respuesta" The Journal of the Operational Research Society, vol. 42, n.º 10 (octubre de 1991), págs. 914-918
- ^ El Instituto de Investigación de Operaciones y Ciencias de la Gestión *En 2008, Thomas L. Saaty recibió el Premio de Impacto INFORMS por su desarrollo del Proceso de Jerarquía Analítica.
- ^ Mari A. Pöyhönen, Raimo P. Hämäläinen, Ahti A. Salo "Un experimento sobre el modelado numérico de declaraciones de proporciones verbales" Journal of Multi-Criteria Decision Analysis, vol 6, no 1, págs. 1-10, 1997
- ^ Stan Schenkerman "Inducción de un orden inexistente mediante el proceso de jerarquía analítica", Decision Sciences, primavera de 1997
- ^ Pérez et al. "Otra posible deficiencia del AHP" TOP: Revista Oficial de la Sociedad Española de Estadística e Investigación Operativa, Volumen 14, Número 1 / Junio, 2006, Springer Berlin/Heidelberg
- ^ Munier, Nolberto (2021). Usos y limitaciones del método AHP. Un análisis no matemático y racional. Gestión para profesionales. Suiza: Springer Nature . doi :10.1007/978-3-030-60392-2. ISBN 978-3-030-60392-2.S2CID241759250 .
- ^ Forman, Ernest H., "Modos de síntesis ideales y distribuidos para el proceso de jerarquía analítica" presentado en la Federación Internacional de Investigación de Operaciones, Lisboa, Portugal, julio de 1993.
- ^ Arroyo, P.; Tommelein, ID; Ballard, G. (enero de 2015). "Comparación de AHP y CBA como métodos de decisión para resolver el problema de elección en el diseño detallado". Journal of Construction Engineering and Management . 141 (1): 04014063. doi :10.1061/(ASCE)CO.1943-7862.0000915.
- ^ Landau, E. (1914). "Über Preisverteilung bei Spielturnieren Archivado el 13 de marzo de 2020 en Wayback Machine . Zeitschrift für Mathematik und Physik , 63 band (1914), p. 192
- ^ Zermelo, E. (1928). Die Berechnung der Turnier-Ergebnisse als ein Maximumproblem der Wahrscheinlichkeitsrechnung , Mathematische Zeitschrift 29, 1929, págs. 436–460
- ^ Hasse, M (1961). "Über die Behandlung graphentheoretischer Probleme unter Verwendung der Matrizenrechnung". Wiss. Tiempo. Tecnología. Univ. Dresde . 10 : 1313–6.
- ^ Ramanujacharyulu, C (1964). "Análisis de experimentos preferenciales". Psychometrika . 29 (3): 257–261. doi :10.1007/bf02289722. S2CID 121033891. Archivado desde el original el 16 de diciembre de 2013.
- ^ Salavati, A., Haghshenas, H., Ghadirifaraz, B., Laghaei, J. y Eftekhari, G. (2016). Aplicación de enfoques AHP y de agrupamiento para la toma de decisiones en materia de transporte público: un estudio de caso de la ciudad de Isfahán. Journal of Public Transportation, 19(4), 3.
Lectura adicional
- Saaty, Thomas L. Toma de decisiones para líderes: el proceso analítico jerárquico para decisiones en un mundo complejo (1982). Belmont, California: Wadsworth. ISBN 0-534-97959-9 ; Tapa blanda, Pittsburgh: RWS. ISBN 0-9620317-0-4 . "Se centra en la aplicación práctica del AHP; cubre brevemente la teoría".
- Saaty, Thomas L. Fundamentos de la toma de decisiones y la teoría de prioridades con el proceso analítico jerárquico (1994). Pittsburgh: RWS. ISBN 0-9620317-6-3 . "Una exposición exhaustiva de los aspectos teóricos del proceso analítico jerárquico".
- Saaty, Thomas L. Principios matemáticos de la toma de decisiones (Principia Mathematica Decernendi) (2009). Pittsburgh: RWS. ISBN 1-888603-10-0 . "Cobertura integral del AHP, su sucesor, el ANP , y desarrollos posteriores de sus conceptos subyacentes".
- Saaty, Thomas L., con Ernest H. Forman. The Hierarchon: A Dictionary of Hierarchies (El jerarca: un diccionario de jerarquías) . (1992) Pittsburgh: RWS. ISBN 0-9620317-5-5 . "Docenas de ilustraciones y ejemplos de jerarquías AHP. Una clasificación inicial de ideas relacionadas con la planificación, la resolución de conflictos y la toma de decisiones".
- Saaty, Thomas L., con Luis G. Vargas La lógica de las prioridades: aplicaciones en los negocios, la energía, la salud y el transporte (1982). Boston: Kluwer-Nijhoff. ISBN 0-89838-071-5 (tapa dura) ISBN 0-89838-078-2 (libro de bolsillo). Reeditado en 1991 por RWS, ISBN 1-888603-07-0 .
- Kardi Teknomo. Tutorial de proceso de jerarquía analítica (2012). Revoledu.
- Kearns, Kevin P.; Saaty, Thomas L. Planificación analítica: la organización de sistemas (1985). Oxford: Pergamon Press. ISBN 0-08-032599-8 . Republicado en 1991 por RWS, ISBN 1-888603-07-0 .
- Con Joyce Alexander. Resolución de conflictos: el proceso analítico jerárquico (1989). Nueva York: Praeger. ISBN 0-275-93229-X
- Vargas, Luis L.; Saaty, Thomas L. Predicción, proyección y pronóstico: aplicaciones del proceso analítico jerárquico en economía, finanzas, política, juegos y deportes (1991). Boston: Kluwer Academic. ISBN 0-7923-9104-7
- Vargas, Luis L.; Saaty, Thomas L. Toma de decisiones en entornos económicos, sociales y tecnológicos (1994). Pittsburgh: RWS. ISBN 0-9620317-7-1
- Vargas, Luis L.; Saaty, Thomas L. Modelos, métodos, conceptos y aplicaciones del proceso analítico jerárquico (2001). Boston: Kluwer Academic. ISBN 0-7923-7267-0
- Peniwati, Kirti; Vargas, Luis L. Toma de decisiones en grupo: identificar y reconciliar diferencias (2007). Pittsburgh: RWS. ISBN 1-888603-08-9
Enlaces externos
- Revista Internacional del Proceso Analítico Jerárquico Una revista en línea sobre la toma de decisiones multicriterio utilizando el AHP.
- easyAHP Herramienta online para tomar decisiones colaborativas utilizando AHP easyAHP es una herramienta online gratuita para tomar decisiones de forma colaborativa o individual. easy AHP utiliza la metodología AHP: Proceso analítico jerárquico.
- Vídeo de AHP. (clip de YouTube de 9:17) Exposición muy completa de AHP por parte del Dr. Klaus Göpel
- Ejemplo de proceso de jerarquía analítica (AHP) con simulaciones usando Matlab – Waqqas Farooq – Ejemplo de AHP para selección de universidades usando Matlab.
- Una guía ilustrada (pdf) – Dr. Oliver Meixner Universidad de Viena – "Proceso analítico jerárquico", un resumen muy fácil de entender de la teoría matemática
- Ejemplo de AHP con implementación de Matlab: explicación de AHP con un ejemplo y código Matlab.
- Paquete R ahp – Un paquete AHP de código abierto.
- AHPy: una implementación de AHP en Python de código abierto con un solucionador óptimo para comparaciones por pares faltantes
- Matemáticas introductorias del proceso de jerarquía analítica: una introducción a las matemáticas del proceso de jerarquía analítica.
- Cómo utilizar AHP para la priorización de proyectos por el Dr. James Brown (seminario web)
- Guía para usar AHP en Excel Una guía para usar AHP en Excel por el Dr. Richard Hodgett
- Utilice la metodología AHP para definir y evaluar de manera más eficaz su enfoque de implementación de SAP por Jeetendra Kumar

