Propiedad de límite superior mínimo

En matemáticas , la propiedad de límite superior mínimo (a veces llamada completitud , propiedad suprema o propiedad lub ) ^[1] es una propiedad fundamental de los números reales . De manera más general, un conjunto parcialmente ordenado X tiene la propiedad de límite superior mínimo si cada subconjunto no vacío de X con un límite superior tiene un límite superior mínimo (supremo) en X. No todos los conjuntos (parcialmente) ordenados tienen la propiedad de límite superior mínimo. Por ejemplo, el conjunto de todos los números racionales con su orden natural no tiene la propiedad de límite superior mínimo.${\displaystyle \mathbb {Q} }$

La propiedad del límite superior mínimo es una forma del axioma de completitud para los números reales, y a veces se la denomina completitud de Dedekind . ^[2] Se puede utilizar para demostrar muchos de los resultados fundamentales del análisis real , como el teorema del valor intermedio , el teorema de Bolzano-Weierstrass , el teorema del valor extremo y el teorema de Heine-Borel . Por lo general, se toma como un axioma en construcciones sintéticas de los números reales , y también está íntimamente relacionado con la construcción de los números reales utilizando cortes de Dedekind .

En la teoría del orden , esta propiedad se puede generalizar a una noción de completitud para cualquier conjunto parcialmente ordenado . Un conjunto ordenado linealmente que es denso y tiene la propiedad de límite superior mínimo se denomina continuo lineal .

Sea S un conjunto no vacío de números reales .

• Un número real x se llama límite superior para S si x ≥ s para todo s ∈ S .
• Un número real x es el límite superior mínimo (o supremo ) para S si x es un límite superior para S y x ≤ y para cada límite superior y de S.

La propiedad del límite superior mínimo establece que cualquier conjunto no vacío de números reales que tenga un límite superior debe tener un límite superior mínimo en números reales .

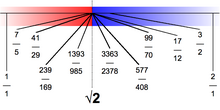
De manera más general, se puede definir un límite superior y un límite superior mínimo para cualquier subconjunto de un conjunto parcialmente ordenado X , reemplazando “número real” por “elemento de X ”. En este caso, decimos que X tiene la propiedad de límite superior mínimo si cada subconjunto no vacío de X con un límite superior tiene un límite superior mínimo en X .

Por ejemplo, el conjunto Q de números racionales no tiene la propiedad de límite superior mínimo bajo el orden habitual. Por ejemplo, el conjunto

${\displaystyle \left\{x\in \mathbf {Q} :x^{2}\leq 2\right\}=\mathbf {Q} \cap \left(-{\sqrt {2}},{\sqrt {2}}\right)}$

tiene un límite superior en Q , pero no tiene un límite superior mínimo en Q (ya que la raíz cuadrada de dos es irracional ). La construcción de los números reales mediante cortes de Dedekind aprovecha esta falla al definir los números irracionales como los límites superiores mínimos de ciertos subconjuntos de los racionales.

La propiedad del límite superior mínimo es equivalente a otras formas del axioma de completitud , como la convergencia de las sucesiones de Cauchy o el teorema de intervalos anidados . El estatus lógico de la propiedad depende de la construcción de los números reales utilizados: en el enfoque sintético , la propiedad suele tomarse como un axioma para los números reales (véase axioma del límite superior mínimo ); en un enfoque constructivo, la propiedad debe demostrarse como un teorema , ya sea directamente a partir de la construcción o como consecuencia de alguna otra forma de completitud.

Es posible demostrar la propiedad de límite superior mínimo utilizando el supuesto de que toda sucesión de Cauchy de números reales converge. Sea S un conjunto no vacío de números reales. Si S tiene exactamente un elemento, entonces su único elemento es un límite superior mínimo. Por lo tanto, considere S con más de un elemento y suponga que S tiene un límite superior B ₁ . Como S no está vacío y tiene más de un elemento, existe un número real A ₁ que no es un límite superior para S . Defina las sucesiones A ₁ , A ₂ , A ₃ , ... y B ₁ , B ₂ , B ₃ , ... recursivamente como sigue:

1. Compruebe si ( A _n + B _n ) ⁄ 2 es un límite superior para S .
2. Si es así, sea A _{n +1} = A _n y sea B _{n +1} = ( A _n + B _n ) ⁄ 2 .
3. De lo contrario, debe haber un elemento s en S tal que s >( A _n + B _n ) ⁄ 2 . Sea A _{n +1} = s y sea B _{n +1} = B _n .

Entonces A ₁ ≤ A ₂ ≤ A ₃ ≤ ⋯ ≤ B ₃ ≤ B ₂ ≤ B ₁ y | A _n − B _n | → 0 cuando n → ∞ . De ello se deduce que ambas sucesiones son de Cauchy y tienen el mismo límite L , que debe ser el límite superior mínimo para S .

La propiedad de límite superior mínimo de R se puede utilizar para demostrar muchos de los principales teoremas fundamentales en el análisis real .

Sea f  : [ a , b ] → R una función continua y supongamos que f  ( a ) < 0 y f  ( b ) > 0 . En este caso, el teorema del valor intermedio establece que f debe tener una raíz en el intervalo [ a , b ] . Este teorema se puede demostrar considerando el conjunto

S  = { s ∈ [ a , b ] :  f  ( x ) < 0 para todo x ≤ s } .

Es decir, S es el segmento inicial de [ a , b ] que toma valores negativos bajo f . Entonces b es un límite superior para S , y el límite superior mínimo debe ser una raíz de f .

El teorema de Bolzano-Weierstrass para R establece que toda sucesión x _n de números reales en un intervalo cerrado [ a , b ] debe tener una subsucesión convergente . Este teorema se puede demostrar considerando el conjunto

S  = { s ∈ [ a , b ] :  s ≤ x _n para infinitos n }

Claramente, , y S no está vacío. Además, b es un límite superior para S , por lo que S tiene un límite superior mínimo c . Entonces c debe ser un punto límite de la secuencia x _n , y se deduce que x _n tiene una subsucesión que converge a c .${\displaystyle a\in S}$

Sea f  : [ a , b ] → R una función continua y sea M = sup f  ([ a , b ]) , donde M = ∞ si f  ([ a , b ]) no tiene límite superior. El teorema del valor extremo establece que M es finito y f  ( c ) = M para algún c ∈ [ a , b ] . Esto se puede demostrar considerando el conjunto

S  = { s ∈ [ a , b ] : sup f  ([ s , b ]) = M } .

Por definición de M , a ∈ S , y por su propia definición, S está acotado por b . Si c es el límite superior mínimo de S , entonces se deduce de la continuidad que f  ( c ) = M .

Sea [ a , b ] un intervalo cerrado en R , y sea { U _α } una colección de conjuntos abiertos que cubre [ a , b ] . Entonces el teorema de Heine-Borel establece que alguna subcolección finita de { U _α } cubre también [ a , b ] . Esta afirmación se puede demostrar considerando el conjunto

S  = { s ∈ [ a , b ] : [ a , s ] puede ser cubierto por un número finito de U _α } .

El conjunto S contiene obviamente a , y está acotado por b por construcción. Por la propiedad de límite superior mínimo, S tiene un límite superior mínimo c ∈ [ a , b ] . Por lo tanto, c es en sí mismo un elemento de algún conjunto abierto U _α , y se sigue para c < b que [ a , c + δ ] puede ser cubierto por un número finito de U _α para algún δ > 0 suficientemente pequeño . Esto prueba que c + δ ∈ S y c no es un límite superior para S . En consecuencia, c = b .

La importancia de la propiedad del límite mínimo superior fue reconocida por primera vez por Bernard Bolzano en su artículo de 1817 Rein analytischer Beweis des Lehrsatzes dass zwischen je zwey Werthen, die ein entgegengesetztes Resultat gewähren, wenigstens eine reelle Wurzel der Gleichung liege . ^[3]

• Lista de temas de análisis reales

• Abbott, Stephen (2001). Understanding Analysis [Comprender el análisis] . Textos de pregrado en matemáticas. Nueva York: Springer-Verlag. ISBN. 0-387-95060-5.
• Aliprantis, Charalambos D ; Burkinshaw, Owen (1998). Principios del análisis real (tercera edición). Académico. ISBN 0-12-050257-7.

• Bartle, Robert G.; Sherbert, Donald R. (2011). Introducción al análisis real (4.ª ed.). Nueva York: John Wiley and Sons. ISBN 978-0-471-43331-6.
• Bressoud, David (2007). Un enfoque radical del análisis real . MAA. ISBN 978-0-88385-747-2.
• Browder, Andrew (1996). Análisis matemático: una introducción . Textos de pregrado en matemáticas . Nueva York: Springer-Verlag. ISBN 0-387-94614-4.
• Dangello, Frank; Seyfried, Michael (1999). Introducción al análisis real . Brooks Cole. ISBN 978-0-395-95933-6.
• Rudin, Walter (1976). Principios del análisis matemático . Walter Rudin Student Series in Advanced Mathematics (3.ª ed.). McGraw–Hill. ISBN 978-0-07-054235-8.
• Willard, Stephen (2004) [1970]. Topología general . Mineola, NY: Dover Publications. ISBN. 9780486434797.