Cruce evitado

This article has an unclear citation style. The references used may be made clearer with a different or consistent style of citation and footnoting. (January 2024) (Learn how and when to remove this message)

En física cuántica y química cuántica , un cruce evitado (a veces llamado cruce intencionado , ^[1] no cruce o anticruzamiento ) es el fenómeno donde dos valores propios de una matriz hermítica que representan un observable cuántico y que dependen de N parámetros reales continuos no pueden volverse iguales en valor ("cruzamiento") excepto en una variedad de N -3 dimensiones. ^[2] El fenómeno también se conoce como teorema de von Neumann-Wigner . En el caso de una molécula diatómica (con un parámetro, a saber, la longitud del enlace ), esto significa que los valores propios no pueden cruzarse en absoluto. En el caso de una molécula triatómica , esto significa que los valores propios pueden coincidir solo en un único punto (ver intersección cónica ).

Esto es particularmente importante en la química cuántica . En la aproximación de Born-Oppenheimer , el hamiltoniano molecular electrónico se diagonaliza en un conjunto de geometrías moleculares distintas (los valores propios obtenidos son los valores de las superficies de energía potencial adiabática ). Las geometrías para las cuales las superficies de energía potencial evitan cruzarse son el lugar geométrico donde falla la aproximación de Born-Oppenheimer.

También se evitan los cruces en las frecuencias de resonancia de sistemas mecánicos no amortiguados, donde las matrices de rigidez y masa son realmente simétricas. En este caso, las frecuencias de resonancia son la raíz cuadrada de los valores propios generalizados.

El estudio de un sistema de dos niveles es de vital importancia en la mecánica cuántica porque incorpora la simplificación de muchos de los sistemas físicamente realizables. El efecto de la perturbación en un hamiltoniano de sistema de dos estados se manifiesta a través de cruces evitados en el gráfico de la curva de energía individual frente a la curva de diferencia de energía de los estados propios. ^[3] El hamiltoniano de dos estados se puede escribir como

${\displaystyle H={\begin{pmatrix}E_{1}&0\\0&E_{2}\end{pmatrix}}\,\!}$

Los valores propios de los cuales son y y los vectores propios , y . Estos dos vectores propios designan los dos estados del sistema. Si el sistema se prepara en cualquiera de los estados, permanecerá en ese estado. Si resulta ser igual a habrá una doble degeneración en el hamiltoniano. En ese caso, cualquier superposición de los estados propios degenerados es evidentemente otro estado propio del hamiltoniano. Por lo tanto, el sistema preparado en cualquier estado permanecerá en ese estado para siempre.${\displaystyle \textstyle E_{1}}$${\displaystyle \textstyle E_{2}}$${\displaystyle \textstyle {\begin{pmatrix}1\\0\end{pmatrix}}}$${\displaystyle \textstyle {\begin{pmatrix}0\\1\end{pmatrix}}}$${\displaystyle \textstyle E_{1}}$${\displaystyle E_{2}}$

Sin embargo, cuando se somete a una perturbación externa , los elementos de la matriz del hamiltoniano cambian. Para simplificar, consideramos una perturbación con solo elementos fuera de la diagonal. Dado que el hamiltoniano general debe ser hermítico, podemos escribir simplemente el nuevo hamiltoniano

${\displaystyle H'=H+P={\begin{pmatrix}E_{1}&0\\0&E_{2}\end{pmatrix}}+{\begin{pmatrix}0&W\\W^{*}&0\end{pmatrix}}={\begin{pmatrix}E_{1}&W\\W^{*}&E_{2}\end{pmatrix}}\,\!}$

Donde P es la perturbación con términos diagonales cero. El hecho de que P sea hermítico fija sus componentes fuera de la diagonal. Los estados propios modificados se pueden encontrar diagonalizando el hamiltoniano modificado. Resulta que los nuevos valores propios y son${\displaystyle \textstyle E_{+}}$${\displaystyle \textstyle E_{-}}$

${\displaystyle E_{\pm }={\frac {E_{1}+E_{2}}{2}}\pm {\sqrt {{\bigg (}{\frac {E_{1}-E_{2}}{2}}{\bigg )}^{2}+|W|^{2}}}}$

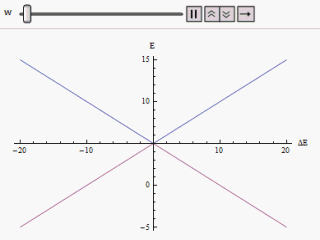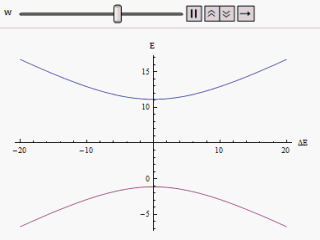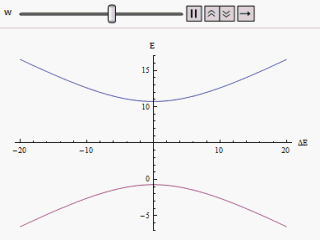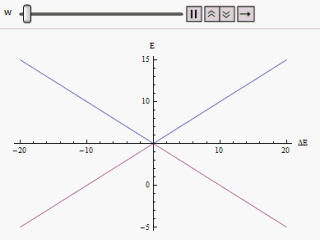
Si se traza un gráfico que varía a lo largo del eje horizontal y /o a lo largo del vertical, encontramos dos ramas de una hipérbola (como se muestra en la figura). La curva se aproxima asintóticamente a los niveles de energía originales no perturbados. Al analizar las curvas, se hace evidente que incluso si los estados originales fueran degenerados (es decir, ), los nuevos estados de energía ya no son iguales. Sin embargo, si se establece en cero, podemos encontrar en , y los niveles se cruzan. Por lo tanto, con el efecto de la perturbación, se evitan estos cruces de nivel.${\displaystyle \textstyle (E_{1}-E_{2})}$${\displaystyle \textstyle E_{+}}$${\displaystyle \textstyle E_{-}}$${\displaystyle \textstyle E_{1}=E_{2}}$${\displaystyle \textstyle W}$${\displaystyle \textstyle (E_{1}-E_{2})=0}$${\displaystyle \textstyle E_{+}=E_{-}}$

El impacto inmediato de evitar el cruce de niveles en un sistema degenerado de dos estados es la aparición de un estado propio de energía reducida. La reducción efectiva de la energía siempre corresponde a una estabilidad creciente (véase: Minimización de la energía ) . La resonancia de enlace en moléculas orgánicas ejemplifica la ocurrencia de tales cruces evitados. Para describir estos casos podemos señalar que los elementos no diagonales en un hamiltoniano diagonalizado anterior no solo modifican los valores propios de energía sino que también superponen los antiguos estados propios en los nuevos. ^[4] Estos efectos son más prominentes si el hamiltoniano original tenía degeneración. Esta superposición de estados propios para lograr más estabilidad es precisamente el fenómeno de la resonancia de enlace químico.

Nuestro tratamiento anterior comenzó denotando los vectores propios y como la representación matricial de los estados propios y de un sistema de dos estados. Usando la notación de bra-ket, los elementos de la matriz de son en realidad los términos${\displaystyle \textstyle {\begin{pmatrix}1\\0\end{pmatrix}}}$${\displaystyle \textstyle {\begin{pmatrix}0\\1\end{pmatrix}}}$${\displaystyle \textstyle |\psi _{1}\rangle }$${\displaystyle \textstyle |\psi _{2}\rangle }$${\displaystyle H'}$

${\displaystyle H'_{ij}=\langle \psi _{i}|H'|\psi _{j}\rangle }$con${\displaystyle i,j\in \left\{{1,2}\right\}}$

donde debido a la degeneración del hamiltoniano no perturbado y las perturbaciones fuera de la diagonal son y .${\displaystyle H'_{11}=H'_{22}=E}$${\displaystyle H'_{12}=W}$${\displaystyle H'_{21}=W^{*}}$

Los nuevos estados propios y se pueden encontrar resolviendo las ecuaciones de valores propios y . A partir de cálculos simples se puede demostrar que${\displaystyle \textstyle |\psi _{+}\rangle }$${\displaystyle \textstyle |\psi _{-}\rangle }$${\displaystyle H'|\psi _{+}\rangle =E_{+}|\psi _{+}\rangle }$${\displaystyle H'|\psi _{-}\rangle =E_{-}|\psi _{-}\rangle }$

${\displaystyle |\psi _{+}\rangle ={\frac {1}{\sqrt {2}}}{\begin{pmatrix}e^{i\phi }\\1\end{pmatrix}}={\frac {1}{\sqrt {2}}}(e^{i\phi }|\psi _{1}\rangle +|\psi _{2}\rangle )}$y

${\displaystyle |\psi _{-}\rangle ={\frac {1}{\sqrt {2}}}{\begin{pmatrix}-e^{i\phi }\\1\end{pmatrix}}={\frac {1}{\sqrt {2}}}(-e^{i\phi }|\psi _{1}\rangle +|\psi _{2}\rangle )}$dónde${\displaystyle e^{i\phi }=W/|W|}$

Es evidente que ambos nuevos estados propios son superposiciones de los estados propios degenerados originales y uno de los valores propios (aquí ) es menor que la energía propia original no perturbada. Por lo tanto, el sistema estable correspondiente mezclará naturalmente los estados propios no perturbados anteriores para minimizar su energía. En el ejemplo del benceno, las evidencias experimentales de estructuras de enlace probables dan lugar a dos estados propios diferentes, y . La simetría de estas dos estructuras exige que .${\displaystyle E_{-}}$${\displaystyle \textstyle |\psi _{1}\rangle }$${\displaystyle \textstyle |\psi _{2}\rangle }$${\displaystyle \langle \psi _{1}|H|\psi _{1}\rangle =\langle \psi _{2}|H|\psi _{2}\rangle =E}$

Sin embargo, resulta que el hamiltoniano de dos estados del benceno no es diagonal. Los elementos no diagonales dan como resultado una disminución de la energía y la molécula de benceno se estabiliza en una estructura que es una superposición de estos elementos simétricos con energía . ^[5] Para cualquier sistema general de dos estados, el cruce de niveles evitado repele los estados propios y, por lo tanto, requiere más energía para que el sistema alcance la configuración de energía más alta.${\displaystyle H}$${\displaystyle E_{-}<E}$${\displaystyle |\psi _{+}\rangle }$${\displaystyle |\psi _{-}\rangle }$

En las moléculas, los acoplamientos no adiabáticos entre dos potenciales adiabáticos construyen la región de cruce evitado (AC). Las resonancias rovibrónicas en la región AC de dos potenciales acoplados son muy especiales, ya que no están en la región de estado ligado de los potenciales adiabáticos, y por lo general no juegan un papel importante en las dispersiones y son menos discutidas. Yu Kun Yang et al estudiaron este problema en New J. Phys. 22 (2020). ^[6] Ejemplificadas en la dispersión de partículas, las resonancias en la región AC se investigan exhaustivamente. Los efectos de las resonancias en la región AC en las secciones transversales de dispersión dependen en gran medida de los acoplamientos no adiabáticos del sistema, pueden ser muy significativos como picos agudos o discretos enterrados en el fondo. Más importante aún, muestra que una cantidad simple propuesta por Zhu y Nakamura para clasificar la fuerza de acoplamiento de las interacciones no adiabáticas puede aplicarse bien para estimar cuantitativamente la importancia de las resonancias en la región AC.

Sin embargo, la ilustración anterior de cruce evitado es un caso muy específico. Desde un punto de vista general, el fenómeno de cruce evitado está controlado en realidad por los parámetros detrás de la perturbación. Para la perturbación más general que afecta a un subespacio bidimensional del hamiltoniano , podemos escribir la matriz hamiltoniana efectiva en ese subespacio como${\displaystyle \textstyle P={\begin{pmatrix}W_{1}&W\\W&W_{2}\end{pmatrix}}}$${\displaystyle H}$

${\displaystyle {\begin{pmatrix}E_{1}&0\\0&E_{2}\end{pmatrix}}+{\begin{pmatrix}W_{1}&W\\W&W_{2}\end{pmatrix}}={\begin{pmatrix}E_{1}+W_{1}&W\\W&E_{2}+W_{2}.\end{pmatrix}}.}$

Aquí los elementos de los vectores de estado se eligieron para que fueran reales de modo que todos los elementos de la matriz se volvieran reales. ^[7] Ahora los valores propios del sistema para este subespacio están dados por

${\displaystyle E_{\pm }={\frac {1}{2}}(E_{1}+E_{2}+W_{1}+W_{2})\pm {\frac {1}{2}}{\sqrt {(E_{1}-E_{2}+W_{1}-W_{2})^{2}+4W^{2}}}}$

Los términos bajo la raíz cuadrada son números reales al cuadrado. Por lo tanto, para que estos dos niveles se crucen simultáneamente, necesitamos

${\displaystyle (E_{1}-E_{2}+W_{1}-W_{2})=0}$

${\displaystyle W=0.}$

Ahora bien, si la perturbación tiene parámetros, en general podemos variar estos números para satisfacer estas dos ecuaciones.${\displaystyle P}$${\displaystyle k}$${\displaystyle {\alpha _{1},\alpha _{2},\alpha _{3}.....\alpha _{k}}}$

${\displaystyle (E_{1}-E_{2}+W_{1}-W_{2})=F_{1}(\alpha _{1},\alpha _{2},\alpha _{3}.....\alpha _{k})=0}$

${\displaystyle W=F_{2}(\alpha _{1},\alpha _{2},\alpha _{3}.....\alpha _{k})=0.}$

Si elegimos los valores de a entonces ambas ecuaciones anteriores tienen un único parámetro libre. En general no es posible encontrar uno tal que ambas ecuaciones se satisfagan. Sin embargo, si permitimos que otro parámetro sea libre, ambas ecuaciones estarán ahora controladas por los mismos dos parámetros. ${\displaystyle \alpha _{1}}$${\displaystyle \alpha _{k-1}}$${\displaystyle \alpha _{k}}$

${\displaystyle F_{1}(\alpha _{k-1},\alpha _{k})|_{\alpha _{1},\alpha _{2},...,\alpha _{k-2}\,fixed}=0}$

${\displaystyle F_{2}(\alpha _{k-1},\alpha _{k})|_{\alpha _{1},\alpha _{2},...,\alpha _{k-2}\,fixed}=0.}$

Y, en general, habrá dos valores de ellos para los cuales las ecuaciones se cumplirán simultáneamente. Por lo tanto, con distintos parámetros, siempre se pueden elegir parámetros de manera arbitraria y, aun así, podemos encontrar dos s de modo que se produzca un cruce de valores propios de energía. En otras palabras, los valores de y serían los mismos para coordenadas que varíen libremente (mientras que el resto de las dos coordenadas se fijan a partir de las ecuaciones de condición). Geométricamente, las ecuaciones de valores propios describen una superficie en el espacio dimensional. ${\displaystyle k}$${\displaystyle k-2}$${\displaystyle \alpha _{k}}$${\displaystyle E_{+}}$${\displaystyle E_{-}}$${\displaystyle k-2}$${\displaystyle k}$

${\displaystyle E_{\pm }=E_{\pm }(\alpha _{1},\alpha _{2},\alpha _{3}.....\alpha _{k}).}$

Puesto que su intersección está parametrizada por coordenadas, podemos afirmar formalmente que para parámetros reales continuos que controlan el hamiltoniano perturbado, los niveles (o superficies) solo pueden cruzarse en una variedad de dimensión . ^[8] Sin embargo, la simetría del hamiltoniano tiene un papel que desempeñar en la dimensionalidad. Si el hamiltoniano original tiene estados asimétricos, , los términos fuera de la diagonal se desvanecen automáticamente para garantizar la hermiticidad. Esto nos permite deshacernos de la ecuación . Ahora bien, a partir de argumentos similares a los planteados anteriormente, es sencillo que para un hamiltoniano asimétrico, la intersección de superficies de energía tiene lugar en una variedad de dimensión . ^[9]${\displaystyle k-2}$${\displaystyle k}$${\displaystyle k-2}$${\displaystyle \langle \psi _{1}|P|\psi _{2}\rangle \neq \langle \psi _{2}|P|\psi _{1}\rangle }$${\displaystyle W=0}$${\displaystyle k-1}$

En una molécula poliatómica N-atómica hay 3N-6 coordenadas vibracionales (3N-5 para una molécula lineal) que entran en el hamiltoniano electrónico como parámetros. Para una molécula diatómica solo hay una de esas coordenadas, la longitud de enlace r. Por lo tanto, debido al teorema de cruce evitado, en una molécula diatómica no podemos tener cruces de nivel entre estados electrónicos de la misma simetría. ^[10] Sin embargo, para una molécula poliatómica hay más de un parámetro geométrico en el hamiltoniano electrónico y no se evitan los cruces de nivel entre estados electrónicos de la misma simetría. ^[11]

• Fase geométrica
• Christopher Longuet-Higgins
• Intersección cónica
• Acoplamiento vibrónico
• Teorema adiabático
• Endurecimiento de la unión
• Suavizado de enlaces
• Fórmula de Landau-Zener
• Repulsión de nivel