Precesión axial
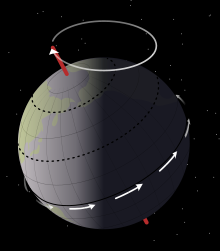
En astronomía , la precesión axial es un cambio lento, continuo y provocado por la gravedad en la orientación del eje de rotación de un cuerpo astronómico . En ausencia de precesión, la órbita del cuerpo astronómico mostraría paralelismo axial . [2] En particular, la precesión axial puede referirse al cambio gradual en la orientación del eje de rotación de la Tierra en un ciclo de aproximadamente 26.000 años. [1] Esto es similar a la precesión de una peonza, con el eje trazando un par de conos unidos en sus vértices . El término "precesión" normalmente se refiere solo a esta parte más grande del movimiento; otros cambios en la alineación del eje de la Tierra ( nutación y movimiento polar ) son de magnitud mucho menor.
La precesión de la Tierra se denominaba históricamente precesión de los equinoccios , porque los equinoccios se movían hacia el oeste a lo largo de la eclíptica en relación con las estrellas fijas , en sentido opuesto al movimiento anual del Sol a lo largo de la eclíptica. Históricamente, [3] el descubrimiento de la precesión de los equinoccios suele atribuirse en Occidente al astrónomo Hiparco del siglo II a. C. Con las mejoras en la capacidad para calcular la fuerza gravitatoria entre los planetas durante la primera mitad del siglo XIX, se reconoció que la propia eclíptica se movía ligeramente, lo que se denominó precesión planetaria , ya en 1863, mientras que el componente dominante se denominó precesión lunisolar . [4] Su combinación se denominó precesión general , en lugar de precesión de los equinoccios.
La precesión lunisolar es causada por las fuerzas gravitacionales de la Luna y el Sol sobre el abultamiento ecuatorial de la Tierra , lo que hace que el eje de la Tierra se mueva con respecto al espacio inercial . La precesión planetaria (un avance) se debe al pequeño ángulo entre la fuerza gravitacional de los otros planetas sobre la Tierra y su plano orbital (la eclíptica), lo que hace que el plano de la eclíptica se desplace ligeramente en relación con el espacio inercial. La precesión lunisolar es aproximadamente 500 veces mayor que la precesión planetaria. [5] Además de la Luna y el Sol, los otros planetas también causan un pequeño movimiento del eje de la Tierra en el espacio inercial, lo que hace que el contraste en los términos lunisolar versus planetario sea engañoso, por lo que en 2006 la Unión Astronómica Internacional recomendó que el componente dominante se renombrara precesión del ecuador , y el componente menor se renombrara precesión de la eclíptica , pero su combinación todavía se llama precesión general. [6] Existen muchas referencias a los términos antiguos en publicaciones anteriores al cambio.
Nomenclatura

El término " precesión " se deriva del latín praecedere ("preceder, venir antes o antes"). Las estrellas vistas desde la Tierra se observan avanzando de este a oeste diariamente, debido al movimiento diurno de la Tierra , y anualmente, debido a la revolución de la Tierra alrededor del Sol. Al mismo tiempo, se puede observar que las estrellas anticipan ligeramente dicho movimiento, a un ritmo de aproximadamente 50 segundos de arco por año, un fenómeno conocido como la "precesión de los equinoccios".
Al describir este movimiento, los astrónomos generalmente han acortado el término simplemente a "precesión". Al describir la causa del movimiento, los físicos también han utilizado el término "precesión", lo que ha llevado a cierta confusión entre el fenómeno observable y su causa, lo cual es importante porque en astronomía, algunas precesiones son reales y otras son aparentes. Esta cuestión se complica aún más por el hecho de que muchos astrónomos son físicos o astrofísicos.
El término "precesión" utilizado en astronomía generalmente describe la precesión observable del equinoccio (las estrellas que se mueven retrógradas en el cielo), mientras que el término "precesión" utilizado en física generalmente describe un proceso mecánico.
Efectos
La precesión del eje de la Tierra tiene una serie de efectos observables. En primer lugar, las posiciones de los polos celestes sur y norte parecen moverse en círculos contra el fondo de estrellas fijo en el espacio, completando un circuito en aproximadamente 26.000 años. Así, mientras que hoy la estrella Polaris se encuentra aproximadamente en el polo norte celeste, esto cambiará con el tiempo, y otras estrellas se convertirán en la " estrella del norte ". [3] En aproximadamente 3.200 años, la estrella Gamma Cephei en la constelación de Cefeo sucederá a Polaris en esta posición. El polo celeste sur carece actualmente de una estrella brillante que marque su posición, pero con el tiempo la precesión también hará que las estrellas brillantes se conviertan en estrellas del sur . A medida que los polos celestes se desplazan, hay un cambio gradual correspondiente en la orientación aparente de todo el campo estelar, visto desde una posición particular en la Tierra.
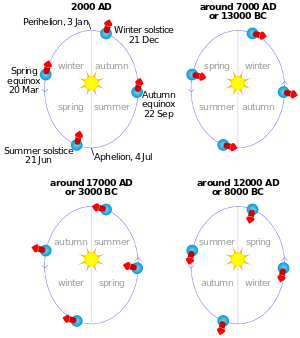
En segundo lugar, la posición de la Tierra en su órbita alrededor del Sol en los solsticios , equinoccios u otros momentos definidos en relación con las estaciones, cambia lentamente. [3] Por ejemplo, supongamos que la posición orbital de la Tierra está marcada en el solsticio de verano, cuando la inclinación axial de la Tierra apunta directamente hacia el Sol. Una órbita completa más tarde, cuando el Sol ha regresado a la misma posición aparente en relación con las estrellas de fondo, la inclinación axial de la Tierra ya no está directamente hacia el Sol: debido a los efectos de la precesión, está un poco "más allá" de esto. En otras palabras, el solsticio ocurrió un poco antes en la órbita. Por lo tanto, el año trópico , que mide el ciclo de las estaciones (por ejemplo, el tiempo de solsticio a solsticio, o de equinoccio a equinoccio), es aproximadamente 20 minutos más corto que el año sideral , que se mide por la posición aparente del Sol en relación con las estrellas. Después de unos 26.000 años, la diferencia asciende a un año completo, por lo que las posiciones de las estaciones en relación con la órbita están "de nuevo donde empezaron". (Otros efectos también cambian lentamente la forma y la orientación de la órbita de la Tierra, y estos, en combinación con la precesión, crean varios ciclos de diferentes períodos; véase también los ciclos de Milankovitch . La magnitud de la inclinación de la Tierra, a diferencia de su orientación, también cambia lentamente con el tiempo, pero este efecto no se atribuye directamente a la precesión).
Por razones idénticas, la posición aparente del Sol en relación con el fondo de estrellas en un momento fijo estacionalmente retrocede lentamente 360° a través de las doce constelaciones tradicionales del zodíaco , a un ritmo de unos 50,3 segundos de arco por año, o 1 grado cada 71,6 años.
En la actualidad, la tasa de precesión corresponde a un período de 25.772 años, por lo que el año tropical es más corto que el año sideral en 1.224,5 segundos (20 min 24,5 s ≈ (365,24219 × 86400) / 25772).
La tasa en sí varía un poco con el tiempo (ver Valores a continuación), por lo que no se puede decir que en exactamente 25.772 años el eje de la Tierra volverá a donde está ahora.
Para más detalles, véase Cambios en las estrellas polares y Cambios polares y equinoccios, más abajo.
Historia
Mundo helenístico
Hiparco
El descubrimiento de la precesión suele atribuirse a Hiparco (190-120 a. C.) de Rodas o Nicea , un astrónomo griego . Según el Almagesto de Ptolomeo , Hiparco midió la longitud de Spica y otras estrellas brillantes. Comparando sus mediciones con los datos de sus predecesores, Timocharis (320-260 a. C.) y Aristilus (~280 a. C.), concluyó que Spica se había movido 2° con respecto al equinoccio de otoño . También comparó las longitudes del año trópico (el tiempo que tarda el Sol en volver a un equinoccio) y el año sideral (el tiempo que tarda el Sol en volver a una estrella fija), y encontró una ligera discrepancia. Hiparco concluyó que los equinoccios se movían ("precesaban") a través del zodíaco, y que la tasa de precesión no era inferior a 1° en un siglo, en otras palabras, completando un ciclo completo en no más de 36.000 años. [7]
Prácticamente todos los escritos de Hiparco se han perdido, incluido su trabajo sobre la precesión. Ptolomeo los menciona, explicando la precesión como la rotación de la esfera celeste alrededor de una Tierra inmóvil. Es razonable suponer que Hiparco, al igual que Ptolomeo, pensaba en la precesión en términos geocéntricos como un movimiento de los cielos, en lugar de un movimiento de la Tierra.
Ptolomeo
El primer astrónomo conocido que continuó el trabajo de Hiparco sobre la precesión fue Ptolomeo en el siglo II d. C. Ptolomeo midió las longitudes de Régulo , Espiga y otras estrellas brillantes con una variación del método lunar de Hiparco que no requería eclipses. Antes del atardecer, midió el arco longitudinal que separa la Luna del Sol. Luego, después del atardecer, midió el arco desde la Luna hasta la estrella. Utilizó el modelo de Hiparco para calcular la longitud del Sol e hizo correcciones para el movimiento de la Luna y su paralaje . [8] Ptolomeo comparó sus propias observaciones con las realizadas por Hiparco, Menelao de Alejandría , Timocharis y Agripa . Descubrió que entre la época de Hiparco y la suya (unos 265 años), las estrellas se habían movido 2° 40', o 1° en 100 años (36" por año; la tasa aceptada hoy es de unas 50" por año o 1° en 72 años). Sin embargo, es posible que Ptolomeo simplemente confiara en la cifra de Hiparco en lugar de hacer sus propias mediciones. También confirmó que la precesión afectaba a todas las estrellas fijas, no sólo a las cercanas a la eclíptica, y su ciclo tenía el mismo período de 36.000 años que el de Hiparco. [7]
Otros autores
La mayoría de los autores antiguos no mencionaron la precesión y, tal vez, no sabían de ella. Por ejemplo, Proclo rechazó la precesión, mientras que Teón de Alejandría , un comentarista de Ptolomeo en el siglo IV, aceptó la explicación de Ptolomeo. Teón también informa una teoría alternativa:
- "Según ciertas opiniones, los astrólogos antiguos creen que a partir de una determinada época los signos solsticiales tienen un movimiento de 8° en el orden de los signos, después del cual retroceden la misma cantidad. ..." (Dreyer 1958, p. 204)
En lugar de recorrer toda la secuencia del zodíaco, los equinoccios se "movían" de un lado a otro en un arco de 8°. Teón presenta la teoría de la "movimiento" como una alternativa a la precesión.
Teorías de descubrimiento alternativas
Babilonios
Se han hecho varias afirmaciones de que otras culturas descubrieron la precesión independientemente de Hiparco. Según Al-Battani , los astrónomos caldeos habían distinguido el año tropical y sideral , de modo que hacia el año 330 a. C. habrían estado en condiciones de describir la precesión, aunque de manera inexacta, pero tales afirmaciones generalmente se consideran infundadas. [9]
maya
La arqueóloga Susan Milbrath ha especulado que el calendario mesoamericano de Cuenta Larga de "30.000 años que incluye las Pléyades ... puede haber sido un esfuerzo por calcular la precesión de los equinoccios". [10] Esta opinión es sostenida por algunos otros estudiosos profesionales de la civilización maya . [ cita requerida ]
Antiguos egipcios
De manera similar, se afirma que la precesión de los equinoccios era conocida en el Antiguo Egipto , antes de la época de Hiparco (el período ptolemaico ). Estas afirmaciones siguen siendo controvertidas. Los antiguos egipcios llevaban calendarios precisos y registraban las fechas en las paredes de los templos, por lo que les resultaría sencillo trazar la tasa de precesión "aproximada".
El Zodíaco de Dendera , un mapa estelar dentro del templo de Hathor en Dendera , supuestamente registra la precesión de los equinoccios. [11] En cualquier caso, si los antiguos egipcios sabían de la precesión, su conocimiento no está registrado como tal en ninguno de sus textos astronómicos sobrevivientes.
Michael Rice, un escritor popular sobre el Antiguo Egipto, ha escrito que los antiguos egipcios deben haber observado la precesión, [12] y sugirió que esta conciencia tuvo profundos efectos en su cultura. [13] Rice señaló que los egipcios reorientaban los templos en respuesta a la precesión de las estrellas asociadas. [14]
India
Antes de 1200, la India tenía dos teorías de trepidación , una con una tasa y otra sin tasa, y varios modelos relacionados de precesión. Cada una tuvo cambios menores o correcciones por varios comentaristas. La dominante de las tres fue la trepidación descrita por el tratado astronómico indio más respetado, el Surya Siddhanta (3:9-12), compuesto c. 400 pero revisado durante los siguientes siglos. Utilizaba una época sideral, o ayanamsa , que todavía se usa en todos los calendarios indios , que varía sobre la longitud eclíptica de 19°11′ a 23°51′, dependiendo del grupo consultado. [15] Esta época hace que los aproximadamente 30 años del calendario indio comiencen 23-28 días después del equinoccio de marzo moderno . El equinoccio de marzo del Surya Siddhanta libraba 27° en ambas direcciones desde la época sideral. Así, el equinoccio se desplazó 54° en una dirección y luego retrocedió 54° en la otra dirección. Este ciclo tardó 7200 años en completarse a un ritmo de 54″/año. El equinoccio coincidió con la época de comienzos del Kali Yuga en −3101 y nuevamente 3600 años después en 499. La dirección cambió de prograda a retrógrada a mitad de camino entre estos años en −1301 cuando alcanzó su desviación máxima de 27°, y habría permanecido retrógrada, la misma dirección que la precesión moderna, durante 3600 años hasta 2299. [16] [17] : 29–30
Varāhamihira ( c. 550 ) describió otra trepidación : un arco de 46°40′ en una dirección y un retorno al punto de partida. La mitad de este arco, 23°20′, se identificó con la declinación máxima del Sol a ambos lados del ecuador en los solsticios, pero no se especificó ningún período, por lo que no se puede determinar una tasa anual. [17] : 27–28
Varios autores han descrito la precesión como cercana a 200.000 revoluciones en un Kalpa de 4.320.000.000 años, lo que sería una tasa de 200.000×360×3600/4.320.000.000 = 60″/año. Probablemente se desviaron de unas 200.000 revoluciones para hacer que la precesión acumulada fuera cero cerca de 500. Visnucandra ( c. 550–600 ) menciona 189.411 revoluciones en un Kalpa o 56,8″/año. Bhaskara I ( c. 600–680 ) menciona [1]94.110 revoluciones en un Kalpa o 58,2″/año. Bhāskara II ( c. 1150 ) menciona 199.699 revoluciones en un Kalpa o 59,9″/año. [17] : 32–33
Astronomía china
Yu Xi (siglo IV d. C.) fue el primer astrónomo chino que mencionó la precesión. Calculó que la velocidad de la precesión era de 1° cada 50 años. [18]
Edad Media y Renacimiento
En la astronomía islámica medieval , la precesión se conocía gracias al Almagesto de Ptolomeo y mediante observaciones que refinaban el valor.
Al-Battani , en su obra Zij Al-Sabi , menciona el cálculo de precesión de Hiparco, y el valor de Ptolomeo de 1 grado por cada 100 años solares, dice que midió la precesión y encontró que era de un grado por cada 66 años solares. [19]
Posteriormente, Al-Sufi , en su Libro de las estrellas fijas , menciona los mismos valores de Ptolomeo para la precesión, que es de 1 grado cada 100 años solares. Luego cita un valor diferente de Zij Al Mumtahan , que se realizó durante el reinado de Al-Ma'mun , de 1 grado cada 66 años solares. También cita al mencionado Zij Al-Sabi de Al-Battani, que ajustó las coordenadas de las estrellas en 11 grados y 10 minutos de arco para tener en cuenta la diferencia entre el tiempo de Al-Battani y el de Ptolomeo. [20]
Más tarde, el Zij-i Ilkhani , compilado en el observatorio de Maragheh , establece la precesión de los equinoccios en 51 segundos de arco por año, lo que está muy cerca del valor moderno de 50,2 segundos de arco. [21]
En la Edad Media, los astrónomos islámicos y cristianos latinos consideraban que la «trepidación» era un movimiento de las estrellas fijas que se sumaba a la precesión. Esta teoría se atribuye habitualmente al astrónomo árabe Thabit ibn Qurra , pero la atribución ha sido cuestionada en los tiempos modernos. Nicolás Copérnico publicó un relato diferente de la trepidación en De revolutionibus orbium coelestium (1543). Esta obra hace la primera referencia definitiva a la precesión como resultado de un movimiento del eje de la Tierra. Copérnico caracterizó la precesión como el tercer movimiento de la Tierra. [22]
Periodo moderno
Más de un siglo después, Isaac Newton en Philosophiae Naturalis Principia Mathematica (1687) explicó la precesión como una consecuencia de la gravitación . [23] Sin embargo, las ecuaciones de precesión originales de Newton no funcionaron y fueron revisadas considerablemente por Jean le Rond d'Alembert y científicos posteriores.
El descubrimiento de Hiparco
Hiparco dio cuenta de su descubrimiento en Sobre el desplazamiento de los puntos solsticiales y equinocciales (descrito en el Almagesto III.1 y VII.2). Midió la longitud eclíptica de la estrella Spica durante los eclipses lunares y descubrió que estaba a unos 6° al oeste del equinoccio de otoño . Al comparar sus propias mediciones con las de Timocharis de Alejandría (un contemporáneo de Euclides , que trabajó con Aristóteles a principios del siglo III a. C.), descubrió que la longitud de Spica había disminuido unos 2° en el ínterin (los años exactos no se mencionan en el Almagesto ). También en VII.2, Ptolomeo da observaciones más precisas de dos estrellas, incluida Spica, y concluye que en cada caso se produjo un cambio de 2° 40' entre 128 a. C. y 139 d. C. Por lo tanto, 1° por siglo o un ciclo completo en 36.000 años, es decir, el período de precesión de Hiparco según lo informado por Ptolomeo; cf. página 328 en la traducción de Toomer del Almagesto, edición de 1998. También notó este movimiento en otras estrellas. Especuló que solo las estrellas cercanas al zodíaco se desplazaban con el tiempo. Ptolomeo llamó a esto su "primera hipótesis" ( Almagesto VII.1), pero no informó ninguna hipótesis posterior que Hiparco pudiera haber ideado. Hiparco aparentemente limitó sus especulaciones, porque solo tenía unas pocas observaciones más antiguas, que no eran muy confiables.
Como los puntos equinocciales no están marcados en el cielo, Hiparco necesitaba la Luna como punto de referencia; utilizó un eclipse lunar para medir la posición de una estrella. Hiparco ya había desarrollado una forma de calcular la longitud del Sol en cualquier momento. Un eclipse lunar ocurre durante la Luna llena , cuando la Luna está en oposición , exactamente a 180° del Sol. Se cree que Hiparco midió el arco longitudinal que separa a Spica de la Luna. A este valor, agregó la longitud calculada del Sol, más 180° para la longitud de la Luna. Hizo el mismo procedimiento con los datos de Timocharis. [24] Observaciones como estos eclipses, por cierto, son la principal fuente de datos sobre cuándo trabajó Hiparco, ya que otra información biográfica sobre él es mínima. Los eclipses lunares que observó, por ejemplo, tuvieron lugar el 21 de abril de 146 a. C. y el 21 de marzo de 135 a. C. [25]
Hiparco también estudió la precesión en Sobre la duración del año . Dos tipos de año son relevantes para comprender su trabajo. El año trópico es el tiempo que tarda el Sol, visto desde la Tierra, en volver a la misma posición a lo largo de la eclíptica (su trayectoria entre las estrellas de la esfera celeste). El año sideral es el tiempo que tarda el Sol en volver a la misma posición con respecto a las estrellas de la esfera celeste. La precesión hace que las estrellas cambien ligeramente su longitud cada año, por lo que el año sideral es más largo que el año trópico. Utilizando observaciones de los equinoccios y solsticios, Hiparco descubrió que la duración del año trópico era de 365+1/4−1/300 días, o 365,24667 días (Evans 1998, p. 209). Comparándolo con la duración del año sideral, calculó que la tasa de precesión no era inferior a 1° en un siglo. A partir de esta información, es posible calcular que su valor para el año sideral era 365+1/4+1/144 días. [26] Al dar una tasa mínima, es posible que haya estado permitiendo errores en la observación.
Para aproximarse a su año trópico, Hiparco creó su propio calendario lunisolar modificando los de Metón y Calipo en De los meses y días intercalares (hoy perdido), como lo describe Ptolomeo en el Almagesto III.1. [27] El calendario babilónico utilizó un ciclo de 235 meses lunares en 19 años desde 499 a. C. (con solo tres excepciones antes de 380 a. C.), pero no utilizó un número específico de días. El ciclo metónico (432 a. C.) asignó 6.940 días a estos 19 años produciendo un año promedio de 365 + 1/4 + 1/76 o 365,26316 días. El ciclo calípico (330 a. C.) eliminó un día de cuatro ciclos metónicos (76 años) para un año promedio de 365 + 1/4 o 365,25 días. Hiparco eliminó un día más de cuatro ciclos calípicos (304 años), creando el ciclo hipárquico con un año promedio de 365+1/4−1/304 o 365,24671 días, que estaba cerca de su año trópico de 365+1/4−1/300 o 365,24667 días.
Las firmas matemáticas de Hiparco se encuentran en el Mecanismo de Antikythera , una antigua computadora astronómica del siglo II a. C. El mecanismo se basa en un año solar, el Ciclo Metónico, que es el período en el que la Luna reaparece en el mismo lugar en el cielo con la misma fase (la Luna llena aparece en la misma posición en el cielo aproximadamente cada 19 años), el ciclo Calípico (que son cuatro ciclos Metónicos y más precisos), el ciclo Saros y los ciclos Exeligmos (tres ciclos Saros para la predicción precisa de eclipses). El estudio del Mecanismo de Antikythera mostró que los antiguos usaban calendarios muy precisos basados en todos los aspectos del movimiento solar y lunar en el cielo. De hecho, el Mecanismo Lunar que es parte del Mecanismo de Antikythera representa el movimiento de la Luna y su fase, durante un tiempo determinado, utilizando un tren de cuatro engranajes con un dispositivo de pasador y ranura que da una velocidad lunar variable que está muy cerca de la segunda ley de Kepler . Es decir, tiene en cuenta el movimiento rápido de la Luna en el perigeo y el movimiento más lento en el apogeo .
Estrellas polares cambiantes

Una consecuencia de la precesión es el cambio de la estrella polar . Actualmente, Polaris es muy adecuada para marcar la posición del polo norte celeste, ya que es una estrella moderadamente brillante con una magnitud visual de 2,1 (variable) y se encuentra a aproximadamente un grado del polo, sin estrellas de brillo similar demasiado cerca. [28]
La estrella polar anterior era Kochab (Beta Ursae Minoris, β UMi, β Ursae Minoris), la estrella más brillante de la cavidad de la Osa Menor, situada a 16 grados de Polaris. Desempeñó esa función desde el año 1500 a. C. hasta el año 500 d. C. [29] En su época no era tan precisa como lo es Polaris en la actualidad. [ 29] Hoy en día, a Kochab y su vecina Pherkad se las conoce como los "Guardianes del Polo" (que significa Polaris). [29]
Por otra parte, Thuban , en la constelación de Draco , que era la estrella polar en el año 3000 a. C., es mucho menos visible con su magnitud 3,67 (una quinta parte del brillo de Polaris); hoy es invisible en los cielos urbanos contaminados por la luz .
Cuando Polaris vuelva a ser la estrella del norte alrededor del año 27.800, estará más lejos del polo de lo que está ahora debido a su movimiento propio , mientras que en el año 23.600 a. C. estaba más cerca del polo.
En este momento, es más difícil encontrar el polo sur celeste en el cielo, ya que esa zona es una porción particularmente anodina del cielo. La estrella nominal del polo sur es Sigma Octantis , que con su magnitud 5,5 es apenas visible a simple vista incluso en condiciones ideales. Sin embargo, eso cambiará entre los siglos 80 y 90, cuando el polo sur celeste pase por la Falsa Cruz .
Esta situación también se puede ver en un mapa estelar. La orientación del polo sur se está moviendo hacia la constelación de la Cruz del Sur . Durante los últimos 2.000 años aproximadamente, la Cruz del Sur ha apuntado al polo sur celeste. Como consecuencia, la constelación es difícil de ver desde latitudes subtropicales del norte, a diferencia de la época de los antiguos griegos . La Cruz del Sur se puede ver desde el norte de Miami (aproximadamente 25° N), pero solo durante el invierno y principios de la primavera.
Cambios polares y cambios de equinoccios


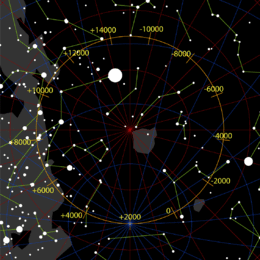
Las imágenes de la derecha intentan explicar la relación entre la precesión del eje de la Tierra y el desplazamiento de los equinoccios. Estas imágenes muestran la posición del eje de la Tierra en la esfera celeste , una esfera ficticia que coloca las estrellas según su posición tal como se ven desde la Tierra, independientemente de su distancia real. La primera imagen muestra la esfera celeste desde el exterior, con las constelaciones en imagen especular. La segunda imagen muestra la perspectiva de una posición cercana a la Tierra vista a través de una lente de ángulo muy amplio (de donde surge la distorsión aparente).
El eje de rotación de la Tierra describe, a lo largo de un período de 25.700 años, un pequeño círculo azul entre las estrellas cerca de la parte superior del diagrama, centrado en el polo norte de la eclíptica (la letra azul E ) y con un radio angular de unos 23,4°, un ángulo conocido como la oblicuidad de la eclíptica . La dirección de la precesión es opuesta a la rotación diaria de la Tierra sobre su eje. El eje marrón era el eje de rotación de la Tierra hace 5.000 años, cuando apuntaba a la estrella Thuban . El eje amarillo, que apunta a Polaris, marca el eje ahora.
Los equinoccios se producen en el punto donde el ecuador celeste se cruza con la eclíptica (línea roja), es decir, donde el eje de la Tierra es perpendicular a la línea que une los centros del Sol y la Tierra. El término "equinoccio" se refiere aquí a un punto de la esfera celeste así definido, en lugar del momento en el que el Sol se encuentra en lo alto del ecuador (aunque los dos significados están relacionados). Cuando el eje precesa de una orientación a otra, el plano ecuatorial de la Tierra (indicado por la cuadrícula circular alrededor del ecuador) se mueve. El ecuador celeste es simplemente el ecuador de la Tierra proyectado sobre la esfera celeste, por lo que se mueve a medida que se mueve el plano ecuatorial de la Tierra, y la intersección con la eclíptica se mueve con él. Las posiciones de los polos y el ecuador en la Tierra no cambian, solo la orientación de la Tierra con respecto a las estrellas fijas.

Como se ve en la cuadrícula marrón , hace 5000 años, el equinoccio de marzo estaba cerca de la estrella Aldebarán en Tauro . Ahora, como se ve en la cuadrícula amarilla, se ha desplazado (indicado por la flecha roja ) a algún lugar de la constelación de Piscis .
Imágenes fijas como éstas son sólo primeras aproximaciones, ya que no tienen en cuenta la velocidad variable de la precesión, la oblicuidad variable de la eclíptica, la precesión planetaria (que es una rotación lenta del propio plano de la eclíptica , actualmente alrededor de un eje situado en el plano, con longitud 174,8764°) y los movimientos propios de las estrellas.
Las eras precesionales de cada constelación, a menudo conocidas como " Grandes Meses ", se dan, aproximadamente, en la siguiente tabla: [30]
| Constelación | Año aproximado | |
|---|---|---|
| Entrando | Saliendo | |
| Tauro | 4500 a. C. | 2000 a. C. |
| Aries | 2000 a. C. | 100 a. C. |
| Piscis | 100 a. C. | 2700 d.C. |
Causa
La precesión de los equinoccios está causada por las fuerzas gravitacionales del Sol y la Luna , y en menor medida de otros cuerpos, sobre la Tierra. Fue explicada por primera vez por Sir Isaac Newton . [31]
La precesión axial es similar a la precesión de una peonza. En ambos casos, la fuerza aplicada se debe a la gravedad. En una peonza, esta fuerza tiende a ser casi paralela al eje de rotación inicialmente y aumenta a medida que la peonza disminuye su velocidad. En el caso de un giroscopio sobre un soporte, puede acercarse a los 90 grados. Sin embargo, en el caso de la Tierra, las fuerzas aplicadas por el Sol y la Luna son más cercanas a la perpendicular al eje de rotación.
La Tierra no es una esfera perfecta sino un esferoide achatado , con un diámetro ecuatorial unos 43 kilómetros mayor que su diámetro polar. Debido a la inclinación axial de la Tierra , durante la mayor parte del año la mitad de este abultamiento que está más cerca del Sol está descentrada, ya sea hacia el norte o hacia el sur, y la mitad más alejada está descentrada en el lado opuesto. La atracción gravitatoria en la mitad más cercana es más fuerte, ya que la gravedad disminuye con el cuadrado de la distancia, por lo que esto crea un pequeño torque en la Tierra ya que el Sol atrae más fuerte en un lado de la Tierra que en el otro. El eje de este torque es aproximadamente perpendicular al eje de rotación de la Tierra por lo que el eje de rotación precesa . Si la Tierra fuera una esfera perfecta, no habría precesión.
Este par medio es perpendicular a la dirección en la que el eje de rotación está inclinado con respecto al polo de la eclíptica, de modo que no cambia la inclinación axial en sí. La magnitud del par del Sol (o de la Luna) varía con el ángulo entre la dirección del eje de rotación de la Tierra y la de la atracción gravitatoria. Se acerca a cero cuando son perpendiculares. Por ejemplo, esto sucede en los equinoccios en el caso de la interacción con el Sol. Esto se puede ver porque los puntos cercano y lejano están alineados con la atracción gravitatoria, por lo que no hay par debido a la diferencia en la atracción gravitatoria.
Aunque la explicación anterior involucraba al Sol, la misma explicación es válida para cualquier objeto que se mueva alrededor de la Tierra, a lo largo o cerca de la eclíptica, en particular, la Luna. La acción combinada del Sol y la Luna se llama precesión lunisolar. Además del movimiento progresivo constante (que resulta en un círculo completo en aproximadamente 25.700 años), el Sol y la Luna también causan pequeñas variaciones periódicas, debido a sus posiciones cambiantes. Estas oscilaciones, tanto en velocidad de precesión como en inclinación axial, se conocen como nutación . El término más importante tiene un período de 18,6 años y una amplitud de 9,2 segundos de arco. [32]
Además de la precesión lunisolar, la acción de los demás planetas del Sistema Solar hace que toda la eclíptica gire lentamente alrededor de un eje cuya longitud eclíptica es de unos 174°, medida en la eclíptica instantánea. Este llamado desplazamiento de la precesión planetaria equivale a una rotación del plano eclíptico de 0,47 segundos de arco por año (más de cien veces menor que la precesión lunisolar). La suma de las dos precesiones se conoce como precesión general.
Ecuaciones

La fuerza de marea sobre la Tierra debida a un cuerpo perturbador (Sol, Luna o planeta) se expresa mediante la ley de gravitación universal de Newton , según la cual la fuerza gravitatoria del cuerpo perturbador en el lado más cercano de la Tierra se dice que es mayor que la fuerza gravitatoria en el lado lejano en una cantidad proporcional a la diferencia en los cubos de las distancias entre los lados cercano y lejano. Si la fuerza gravitatoria del cuerpo perturbador que actúa sobre la masa de la Tierra como una masa puntual en el centro de la Tierra (que proporciona la fuerza centrípeta que causa el movimiento orbital) se resta de la fuerza gravitatoria del cuerpo perturbador en cualquier parte de la superficie de la Tierra, lo que queda puede considerarse como la fuerza de marea. Esto da la noción paradójica de una fuerza que actúa alejándose del satélite pero, en realidad, es simplemente una fuerza menor hacia ese cuerpo debido al gradiente en el campo gravitatorio. Para la precesión, esta fuerza de marea se puede agrupar en dos fuerzas que solo actúan sobre el abultamiento ecuatorial fuera de un radio esférico medio. Este par se puede descomponer en dos pares de componentes, un par paralelo al plano ecuatorial de la Tierra hacia y desde el cuerpo perturbador que se cancelan entre sí, y otro par paralelo al eje de rotación de la Tierra, ambos hacia el plano eclíptico . [33] El último par de fuerzas crea el siguiente vector de torsión en el abultamiento ecuatorial de la Tierra: [5]
dónde
- GM , parámetro gravitacional estándar del cuerpo perturbador
- r , distancia geocéntrica al cuerpo perturbador
- C , momento de inercia alrededor del eje de rotación de la Tierra.
- A , momento de inercia alrededor de cualquier diámetro ecuatorial de la Tierra
- C − A , momento de inercia del abultamiento ecuatorial de la Tierra ( C > A )
- δ , declinación del cuerpo perturbador (norte o sur del ecuador)
- α , ascensión recta del cuerpo perturbador (este a partir del equinoccio de marzo ).
Los tres vectores unitarios del torque en el centro de la Tierra (de arriba a abajo) son x en una línea dentro del plano eclíptico (la intersección del plano ecuatorial de la Tierra con el plano eclíptico) dirigida hacia el equinoccio de marzo, y en una línea en el plano eclíptico dirigida hacia el solsticio de verano (90° al este de x ), y z en una línea dirigida hacia el polo norte de la eclíptica.
El valor de los tres términos sinusoidales en la dirección de x (sin δ cos δ sin α ) para el Sol es una forma de onda de seno cuadrado que varía de cero en los equinoccios (0°, 180°) a 0,36495 en los solsticios (90°, 270°). El valor en la dirección de y (sin δ cos δ (−cos α )) para el Sol es una onda sinusoidal que varía de cero en los cuatro equinoccios y solsticios a ±0,19364 (un poco más de la mitad del pico de seno cuadrado) a mitad de camino entre cada equinoccio y solsticio con picos ligeramente sesgados hacia los equinoccios (43,37°(−), 136,63°(+), 223,37°(−), 316,63°(+)). Ambas formas de onda solares tienen aproximadamente la misma amplitud de pico a pico y el mismo período, la mitad de una revolución o la mitad de un año. El valor en la dirección de z es cero.
El par medio de la onda sinusoidal en la dirección de y es cero para el Sol o la Luna, por lo que este componente del par no afecta a la precesión. El par medio de la forma de onda seno al cuadrado en la dirección de x para el Sol o la Luna es:
dónde
- , semieje mayor de la órbita de la Tierra (Sol) o de la órbita de la Luna
- e , excentricidad de la órbita de la Tierra (Sol) o de la órbita de la Luna
y 1/2 representa el promedio de la forma de onda del seno al cuadrado, representa la distancia promedio al cubo del Sol o la Luna desde la Tierra a lo largo de toda la órbita elíptica, [34] y ε (el ángulo entre el plano ecuatorial y el plano eclíptico) es el valor máximo de δ para el Sol y el valor máximo promedio para la Luna durante un ciclo completo de 18,6 años.
La precesión es:
donde ω es la velocidad angular de la Tierra y Cω es el momento angular de la Tierra . Por lo tanto, el componente de primer orden de la precesión debido al Sol es: [5]
mientras que la debida a la Luna es:
donde i es el ángulo entre el plano de la órbita de la Luna y el plano de la eclíptica. En estas dos ecuaciones, los parámetros del Sol están entre corchetes etiquetados como S, los parámetros de la Luna están entre corchetes etiquetados como L y los parámetros de la Tierra están entre corchetes etiquetados como E. El término representa la inclinación de la órbita de la Luna con respecto a la eclíptica. El término ( C − A )/ C es la elipticidad dinámica o aplanamiento de la Tierra , que se ajusta a la precesión observada porque la estructura interna de la Tierra no se conoce con suficiente detalle. Si la Tierra fuera homogénea, el término sería igual a su tercera excentricidad al cuadrado , [35]
donde a es el radio ecuatorial (6 378 137 m ) y c es el radio polar (6 356 752 m ), por lo que e 2 = 0,003358481 .
Los parámetros aplicables para J2000.0 redondeados a siete dígitos significativos (excluyendo el 1 inicial) son: [36] [37]
| Sol | Luna | Tierra |
|---|---|---|
| GM = 1,3271244 × 1020 m3/ s2 | GM = 4,902799 × 1012 m3/ s2 | ( C − A )/ C = 0,003273763 |
| a = 3,833978 × 108 metros | a = 1,4959802 × 1011 millones | |
| y = 0,05554553 | y = 0,016708634 | |
| yo = 5,156690° | ε = 23,43928° | |
| ω = 7,292115 × 10 −5 rad/s |
que rinde
- dψS /dt = 2,450183 × 10 −12 /s
- dψL /dt = 5,334529 × 10 −12 /s
ambos deben convertirse a ″/a (segundos de arco/año) por el número de segundos de arco en 2 π radianes (1,296 × 106 ″/2π) y el número de segundos en un año (un año juliano ) (3,15576 × 107 s/a):
- dψ S /dt = 15,948788″/a frente a 15,948870″/a de Williams [5]
- dψ L /dt = 34,723638″/a frente a 34,457698″/a de Williams.
La ecuación solar es una buena representación de la precesión debida al Sol porque la órbita de la Tierra es cercana a una elipse y solo se ve ligeramente perturbada por los otros planetas. La ecuación lunar no es una representación tan buena de la precesión debida a la Luna porque la órbita de la Luna está muy distorsionada por el Sol y ni el radio ni la excentricidad son constantes a lo largo del año.
Valores
El cálculo de Simon Newcomb a finales del siglo XIX para la precesión general ( p ) en longitud dio un valor de 5.025,64 segundos de arco por siglo trópico, y fue el valor generalmente aceptado hasta que los satélites artificiales proporcionaron observaciones más precisas y las computadoras electrónicas permitieron calcular modelos más elaborados. Jay Henry Lieske desarrolló una teoría actualizada en 1976, donde p es igual a 5.029,0966 segundos de arco (o 1,3969713 grados) por siglo juliano. Las técnicas modernas como VLBI y LLR permitieron mayores refinamientos, y la Unión Astronómica Internacional adoptó un nuevo valor constante en 2000, y nuevos métodos de cálculo y expresiones polinómicas en 2003 y 2006; la precesión acumulada es: [38]
- p A = 5.028,796195 T + 1,1054348 T 2 + términos de orden superior, en segundos de arco, con T , el tiempo en siglos julianos (es decir, 36.525 días) desde la época de 2000 .
La tasa de precesión es la derivada de:
- p = 5,028.796195 + 2.2108696 T + términos de orden superior.
El término constante de esta velocidad (5.028,796195 segundos de arco por siglo en la ecuación anterior) corresponde a un círculo completo de precesión en 25.771,57534 años (un círculo completo de 360 grados dividido por 50,28796195 segundos de arco por año) [38] aunque algunas otras fuentes sitúan el valor en 25.771,4 años, lo que deja una pequeña incertidumbre.
La tasa de precesión no es una constante, sino que (por el momento) aumenta lentamente con el tiempo, como lo indican los términos lineales (y de orden superior) en T . En cualquier caso, debe enfatizarse que esta fórmula solo es válida durante un período de tiempo limitado . Es una expresión polinómica centrada en el dato J2000, ajustada empíricamente a datos observacionales, no a un modelo determinista del Sistema Solar . Está claro que si T se vuelve lo suficientemente grande (lejano en el futuro o lejano en el pasado), el término T ² dominará y p alcanzará valores muy grandes. En realidad, cálculos más elaborados sobre el modelo numérico del Sistema Solar muestran que la tasa de precesión tiene un período de aproximadamente 41.000 años, el mismo que la oblicuidad de la eclíptica. Es decir,
- p = A + BT + CT 2 + …
es una aproximación de
- p = a + b sen (2π T / P ), donde P es el período de 41.000 años.
Los modelos teóricos pueden calcular las constantes (coeficientes) correspondientes a las potencias más altas de T , pero como es imposible que un polinomio coincida con una función periódica sobre todos los números, la diferencia en todas esas aproximaciones crecerá sin límite a medida que T aumenta. Se puede obtener una precisión suficiente durante un lapso de tiempo limitado ajustando un polinomio de orden suficientemente alto a los datos de observación, en lugar de un modelo numérico dinámico necesariamente imperfecto. [ aclaración necesaria ] Para los cálculos actuales de trayectoria de vuelo de satélites artificiales y naves espaciales, el método polinomial brinda una mejor precisión. En ese sentido, la Unión Astronómica Internacional ha elegido la teoría disponible mejor desarrollada. Hasta unos pocos siglos en el pasado y el futuro, ninguna de las fórmulas utilizadas diverge mucho. Hasta unos pocos miles de años en el pasado y el futuro, la mayoría concuerda con cierta precisión. Para eras más lejanas, las discrepancias se vuelven demasiado grandes: la tasa exacta y el período de precesión pueden no calcularse utilizando estos polinomios incluso para un solo período de precesión completo.
La precesión del eje de la Tierra es un efecto muy lento, pero con el nivel de precisión con el que trabajan los astrónomos, es necesario tenerlo en cuenta a diario. Aunque la precesión y la inclinación del eje de la Tierra (la oblicuidad de la eclíptica) se calculan a partir de la misma teoría y, por lo tanto, están relacionadas entre sí, los dos movimientos actúan de forma independiente, moviéndose en direcciones opuestas. [ aclaración necesaria ]
La tasa de precesión muestra una disminución secular debido a la disipación de mareas de 59"/a a 45"/a (a = annum = año juliano ) durante el período de 500 millones de años centrado en el presente. Después de promediar las fluctuaciones de corto plazo (decenas de miles de años), la tendencia de largo plazo se puede aproximar mediante los siguientes polinomios para el tiempo negativo y positivo desde el presente en "/a, donde T está en miles de millones de años julianos (Ga): [39]
- p − = 50,475838 − 26,368583 T + 21,890862 T 2
- p + = 50,475838 − 27,000654 T + 15,603265 T2
Esto da como resultado una duración media del ciclo actual de 25.676 años.
La precesión será mayor que p + en la pequeña cantidad de +0,135052"/a entre +30 Ma y +130 Ma . El salto a este exceso sobre p + ocurrirá en sólo 20 Ma a partir de ahora porque la disminución secular en la precesión está empezando a cruzar una resonancia en la órbita de la Tierra causada por los otros planetas.
Según WR Ward, en unos 1.500 millones de años, cuando la distancia de la Luna, que aumenta continuamente por los efectos de las mareas, haya aumentado de los 60,3 actuales a aproximadamente 66,5 radios terrestres, las resonancias de los efectos planetarios empujarán la precesión a 49.000 años al principio, y luego, cuando la Luna alcance 68 radios terrestres en unos 2.000 millones de años, a 69.000 años. Esto también estará asociado con grandes oscilaciones en la oblicuidad de la eclíptica. Ward, sin embargo, utilizó el valor moderno anormalmente grande para la disipación de mareas. [40] Usando el promedio de 620 millones de años proporcionado por ritmitas de marea de aproximadamente la mitad del valor moderno, estas resonancias no se alcanzarán hasta aproximadamente 3.000 y 4.000 millones de años, respectivamente. Sin embargo, debido al aumento gradual de la luminosidad del Sol, los océanos de la Tierra se habrán vaporizado antes de ese momento (dentro de unos 2.100 millones de años).
Véase también
- Nutación astronómica
- Inclinación axial
- Ángulos de Euler
- Longitud del equinoccio de primavera
- Ciclos de Milankovitch
- Movimiento polar
- Año sideral
- Precesión absidal
Referencias
- ^ ab Hohenkerk, CY, Yallop, BD, Smith, CA, y Sinclair, AT "Sistemas de referencia celestial" en Seidelmann, PK (ed.) Suplemento explicativo del Almanaque astronómico . Sausalito: University Science Books. pág. 99.
- ^ Lerner, K. Lee; Lerner, Brenda Wilmoth (2003). El mundo de las ciencias de la Tierra . Farmington Hills, MI: Thomson-Gale. pág. 105 y 454. ISBN 0-7876-9332-4. OCLC 60695883.
Durante la revolución alrededor del Sol, el eje polar de la Tierra exhibe paralelismo con Polaris (también conocida como la Estrella del Norte). Aunque se observa paralelismo, la orientación del eje polar de la Tierra exhibe precesión (un bamboleo circular exhibido por los giroscopios) que resulta en un ciclo de precesión de 28.000 años de duración. Actualmente, el eje polar de la Tierra apunta aproximadamente en la dirección de Polaris (la Estrella del Norte). Como resultado de la precesión, durante los próximos 11.000 años, el eje de la Tierra precesará o se tambaleará de modo que asumirá una orientación hacia la estrella Vega.
- ^ abc Astro 101 – Precesión del equinoccio Archivado el 2 de enero de 2009 en Wayback Machine , Western Washington University Planetarium . Consultado el 30 de diciembre de 2008
- ^ Robert Main, Astronomía práctica y esférica (Cambridge: 1863) págs. 203–4.
- ^ abcd Williams, James G. (1994). "Contribución a la tasa de oblicuidad, precesión y nutación de la Tierra". The Astronomical Journal . 108 : 711. Bibcode :1994AJ....108..711W. doi : 10.1086/117108 . S2CID 122370108.
- ^ "Resolución B1 de la IAU de 2006: Adopción de la teoría de precesión P03 y definición de la eclíptica" (PDF) . Archivado desde el original (PDF) el 21 de octubre de 2011. Consultado el 28 de febrero de 2009 .
- ^ ab Ptolomeo (1998) [1984 c. 150 ], Almagesto de Ptolomeo , traducido por Toomer, GJ , Princeton University Press, págs. 131-141, 321-340, ISBN 0-691-00260-6
- ^ Evans 1998, págs. 251-255
- ^ Neugebauer, O. (1950). "El supuesto descubrimiento babilónico de la precesión de los equinoccios". Revista de la Sociedad Oriental Americana . 70 (1): 1–8. doi :10.2307/595428. JSTOR 595428.
- ^ Susan Milbrath, "¿Cuán precisa es la astronomía maya?", boletín del Instituto de Estudios Mayas, diciembre de 2007.
- ^ Tompkins, 1971
- ^ Rice, Michael. El legado de Egipto , pág. 128). "No se sabe con certeza si los antiguos conocían o no la mecánica de la precesión antes de su definición por Hiparco de Bitinia en el siglo II a. C., pero como observadores dedicados del cielo nocturno no podían dejar de ser conscientes de sus efectos".
- ^ Rice, p. 10 "...la precesión es fundamental para comprender lo que impulsó el desarrollo de Egipto"; p. 56 "...en cierto sentido, Egipto como estado-nación y el rey de Egipto como dios viviente son productos de la comprensión por parte de los egipcios de los cambios astronómicos efectuados por el inmenso movimiento aparente de los cuerpos celestes que implica la precesión".
- ^ Rice, p. 170 "alterar la orientación de un templo cuando la estrella en cuya posición había sido fijado originalmente movió su posición como consecuencia de la Precesión, algo que parece haber sucedido varias veces durante el Imperio Nuevo".
- ^ Gobierno de la India (1955), Informe del Comité de Reforma del Calendario (PDF) , Consejo de Investigación Científica e Industrial, pág. 262,
Las longitudes del primer punto de Aries, según las dos escuelas, difieren por lo tanto en 23°[51]′ (–) 19°11′ ... [El límite superior se incrementó en 42′ de precesión acumulada 1950-2000.]
- ^ Surya (1935) [1860], Gangooly, Phanindralal (ed.), Traducción de Surya Siddhanta: Un libro de texto de astronomía hindú, traducido por Burgess, Ebenezzer, Universidad de Calcuta, pág. 114
- ^ abc Pingree, David (1972), "Precesión y trepidación en la astronomía india antes del año 1200 d. C.", Journal for the History of Astronomy , 3 : 27–35, Bibcode :1972JHA.....3...27P, doi :10.1177/002182867200300104, S2CID 115947431
- ^ Pannekoek 1961, pág. 92
- ^ Al-Battani. "Zij Al-Sabi'". Archivado desde el original el 5 de enero de 2017 . Consultado el 30 de septiembre de 2017 .
- ^ Al-Sufi. "Libro de las estrellas fijas".
- ^ Rufus, WC (mayo de 1939). "La influencia de la astronomía islámica en Europa y el Lejano Oriente". Astronomía popular . 47 (5): 233–238 [236]. Código Bibliográfico :1939PA.....47..233R..
- ^ Gillispie, Charles Coulston (1960). El límite de la objetividad: un ensayo sobre la historia de las ideas científicas. Princeton University Press. pág. 24. ISBN 0-691-02350-6.
- ^ Evans 1998, pág. 246
- ^ Evans 1998, pág. 251
- ^ Toomer 1984, pág. 135 n. 14
- ^ Toomer 1978, pág. 218
- ^ Toomer 1984, pág. 139
- ^ van Leeuwen, F. (2007). "CADERA 11767". Hipparcos, la Nueva Reducción . Consultado el 1 de marzo de 2011 .
- ^ abc Benningfield, Damond (14 de junio de 2015). "Kochab". Revista Stardate . Observatorio McDonald de la Universidad de Texas . Consultado el 14 de junio de 2015 .
- ^ Kaler, James B. (2002). El cielo en constante cambio: una guía para la esfera celestial (reimpresión). Cambridge University Press. pág. 152. ISBN 978-0521499187.
- ^ "precesión de los equinoccios | Infoplease". infoplease.com .
- ^ "Conceptos básicos de los vuelos espaciales, capítulo 2". Laboratorio de Propulsión a Chorro . Laboratorio de Propulsión a Chorro/NASA. 29 de octubre de 2013 . Consultado el 26 de marzo de 2015 .
- ^ Ivan I. Mueller , Astronomía esférica y práctica aplicada a la geodesia (Nueva York: Frederick Unger, 1969) 59.
- ^ G. Boué y J. Laskar, "Precesión de un planeta con un satélite", Icarus 185 (2006) 312–330, pág.329.
- ^ George Biddel Airy, Tratados matemáticos sobre las teorías lunares y planetarias, la figura de la Tierra, la precesión y la nutación, el cálculo de variaciones y la teoría ondulatoria de la óptica (tercera edición, 1842) 200.
- ^ Simon, JL; Bretagnon, P.; Chapront, J.; Chapront-Touze, M.; Francou, G.; Laskar, J. (1994). "Expresiones numéricas para fórmulas de precesión y elementos medios para la Luna y los planetas". Astronomía y Astrofísica . 282 : 663. Bibcode :1994A&A...282..663S.
- ^ Dennis D. McCarthy, Nota técnica 13 del IERS: Normas del IERS (1992) (Posdata: utilice XConvert).
- ^ ab N. Capitaine y col. 2003, pág. 581 expresión 39
- ^ Laskar, J.; Robutel, P.; Joutel, F.; Gastineau, M.; Correia, ACM; Levrard, B. (2004). "Una solución numérica a largo plazo para las cantidades de insolación de la Tierra". Astronomía y Astrofísica . 428 : 261–285. Bibcode :2004A&A...428..261L. doi : 10.1051/0004-6361:20041335 .
- ^ Ward, WR (1982). "Comentarios sobre la estabilidad a largo plazo de la oblicuidad de la Tierra". Icarus . 50 (2–3): 444–448. Bibcode :1982Icar...50..444W. doi :10.1016/0019-1035(82)90134-8.
Bibliografía
- Berger, AL (1976). "Oblicuidad y precesión durante los últimos 5000000 años". Astronomía y Astrofísica . 51 (1): 127–135. Bibcode :1976A&A....51..127B.
- Capitaine, N. (2003). "Expresiones para magnitudes de precesión de la UAI en el año 2000". Astronomía y Astrofísica . 412 (2): 567–586. Bibcode :2003A&A...412..567C. doi : 10.1051/0004-6361:20031539 .
- Dreyer, JLE Una historia de la astronomía desde Tales hasta Kepler . 2.ª ed. Nueva York: Dover, 1953.
- Evans, James. Historia y práctica de la astronomía antigua . Nueva York: Oxford University Press, 1998.
- Suplemento explicativo de las Efemérides astronómicas y del Almanaque americano de Efemérides y Náutica
- Hilton, JL (2006). "Informe del Grupo de trabajo de la División I de la Unión Astronómica Internacional sobre precesión y eclíptica" (PDF) . Mecánica celeste y astronomía dinámica . 94 (3): 351–367. Bibcode :2006CeMDA..94..351H. doi :10.1007/s10569-006-0001-2. S2CID 122358401.
- Lieske, JH; Lederle, T.; Fricke, W. (1977). "Expresiones para las magnitudes de precesión basadas en el sistema de constantes astronómicas de la UAI (1976)". Astron. Astrophysics . 58 : 1–16. Bibcode :1977A&A....58....1L.
- La precesión y la oblicuidad de la eclíptica tienen una comparación de valores predichos por diferentes teorías
- Pannekoek, A. Una historia de la astronomía . Nueva York: Dover, 1961.
- Parker, Richard A. "Astronomía egipcia, astrología y cálculo calendárico". Diccionario de biografía científica 15:706–727.
- Rice, Michael (1997), El legado de Egipto: Los arquetipos de la civilización occidental, 3000-30 a. C. , Londres y Nueva York.
- Schütz, Michael (2000). "Hipparch und die Entdeckung der Präzession. Bemerkungen zu David Ulansey, Die Ursprünge des Mithraskultes". Revista electrónica de estudios mitraicos (en alemán). 1 . Archivado desde el original el 4 de noviembre de 2013.
- Simon, JL (1994). "Expresiones numéricas para fórmulas de precesión y elementos medios para la Luna y los planetas". Astronomía y Astrofísica . 282 : 663–683. Bibcode :1994A&A...282..663S.
- Tompkins, Peter . Secretos de la Gran Pirámide . Con un apéndice de Livio Catullo Stecchini. Nueva York: Harper Colophon Books, 1971.
- Toomer, GJ "Hipparchus". Diccionario de biografía científica . Vol. 15:207–224. Nueva York: Charles Scribner's Sons, 1978.
- Toomer, GJ Almagesto de Ptolomeo . Londres: Duckworth, 1984.
- Ulansey, David. Los orígenes de los misterios mitraicos: cosmología y salvación en el mundo antiguo . Nueva York: Oxford University Press, 1989.
- Vondrak, J.; Capitaine, N.; Wallace, P. (2011). "Nuevas expresiones de precesión, válidas para intervalos de tiempo largos". Astronomy & Astrophysics . 534 : A22. Bibcode :2011A&A...534A..22V. doi : 10.1051/0004-6361/201117274 .
Enlaces externos
- El debate de D'Alembert y Euler sobre la solución de la precesión de los equinoccios
- Bowley, Roger; Merrifield, Michael. "Precesión axial". Sesenta símbolos . Brady Haran para la Universidad de Nottingham .
- Precesión forzada y nutación de la Tierra





![{\displaystyle {\frac {d\psi _{S}}{dt}}={\frac {3}{2}}[{\frac {GM}{a^{3}(1-e^{2}\right)^{\frac {3}{2}}}}\right]_{S}[{\frac {CA}{C}}{\frac {\cos \epsilon }{\omega }}\right]_{E}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/741c974dbc1a5365103f19e45facc860fac97750)
![{\displaystyle {\frac {d\psi _{L}}{dt}}={\frac {3}{2}}[{\frac {GM\(1-1.5\sin ^{2}i\right)}{a^{3}(1-e^{2}\right)^{\frac {3}{2}}}}\right]_{L}[{\frac {CA}{C}}{\frac {\cos \epsilon }{\omega }}\right]_{E}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84fcb83cb95c40845bcebddb86b88d643a680182)









