Poligrama (geometría)
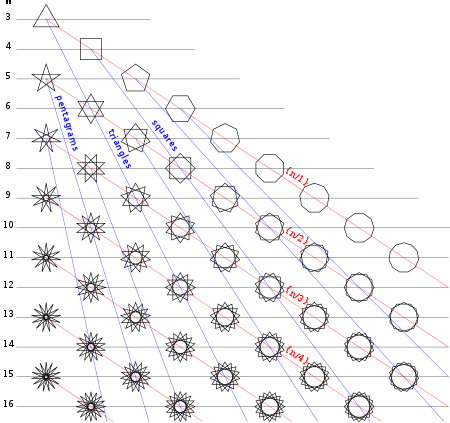
En geometría , un polígono generalizado puede denominarse poligrama y se le puede dar un nombre específico por su número de lados. Todos los polígonos son poligramas, pero también pueden incluir conjuntos de aristas desconectadas, llamados polígonos compuestos . Por ejemplo, un pentagrama regular , {5/2}, tiene 5 lados, y el hexagrama regular , {6/2} o 2{3}, tiene 6 lados divididos en dos triángulos.
Un poligrama regular { p / q } puede estar en un conjunto de polígonos estrellados regulares (para mcd ( p , q ) = 1, q > 1) o en un conjunto de compuestos de polígonos regulares (si mcd( p , q ) > 1). [1]
Etimología
Los nombres de los poligramas combinan un prefijo numeral , como penta- , con el sufijo griego -gram (en este caso generando la palabra pentagrama ). El prefijo normalmente es un cardinal griego , pero existen sinónimos que utilizan otros prefijos. El sufijo -gramo deriva de γραμμῆς ( grammos ), que significa línea. [2]
Polígonos regulares generalizados
Un poligrama regular, como un polígono regular general , se denota por su símbolo de Schläfli { p / q }, donde p y q son primos entre sí (no comparten factores) y q ≥ 2. Para los números enteros p y q , se puede considerar que se construye conectando cada punto q de p puntos espaciados regularmente en una disposición circular. [3] [1]
 {5/2} |  {7/2} |  {7/3} |  {8/3} |  {9/2} |  {9/4} |  {10/3} ... |
Polígonos compuestos regulares
En otros casos en los que n y m tienen un factor común, un poligrama se interpreta como un polígono inferior, { n / k , m / k }, con k = mcd( n , m ), y las copias rotadas se combinan como un polígono compuesto. Estas figuras se denominan polígonos compuestos regulares .
| Triángulos... | Cuadrícula... | Pentágonos... | Pentagramas... | ||||
|---|---|---|---|---|---|---|---|
.svg/1280px-Regular_star_figure_2(3,1).svg.png) {6/2}= 2{3} | .svg/1280px-Regular_star_figure_3(3,1).svg.png) {9/3}= 3{3} | .svg/1280px-Regular_star_figure_4(3,1).svg.png) {12/4}= 4{3} | .svg/1280px-Regular_star_figure_2(4,1).svg.png) {8/2}= 2{4} | .svg/1280px-Regular_star_figure_3(4,1).svg.png) {12/3}= 3{4} | .svg/1280px-Regular_star_figure_2(5,1).svg.png) {10/2}= 2{5} | .svg/1280px-Regular_star_figure_2(5,2).svg.png) {10/4}= 2{5/2} | .svg/1280px-Regular_star_figure_3(5,2).svg.png) {15/6}= 3{5/2} |
.svg){kind=link}
.svg){kind=link}
.svg){kind=link}
.svg){kind=link}
.svg){kind=link}
.svg){kind=link}
.svg){kind=link}
.svg){kind=link}
Véase también
Referencias
- ^ ab Weisstein, Eric W. "Poligrama". MundoMatemático .
- ^ γραμμή, Henry George Liddell, Robert Scott, Un léxico griego-inglés , sobre Perseo
- ^ Coxeter, Harold Scott Macdonald (1973). Politopos regulares . Courier Dover Publications. pág. 93. ISBN 978-0-486-61480-9.
- Cromwell, P.; Poliedros , CUP, Hbk. 1997, ISBN 0-521-66432-2 . Pbk. (1999), ISBN 0-521-66405-5 . pág. 175
- Grünbaum, B. y GC Shephard; Azulejos y patrones , Nueva York: WH Freeman & Co., (1987), ISBN 0-7167-1193-1 .
- Grünbaum, B.; Poliedros con caras huecas, Actas de la Conferencia OTAN-ASI sobre politopos... etc. (Toronto 1993) , ed. T. Bisztriczky et al., Kluwer Academic (1994) págs. 43–70.
- John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Capítulo 26, págs. 404: Politopos estelares regulares, dimensión 2)
- Robert Lachlan, Tratado elemental de geometría pura moderna . Londres: Macmillan, 1893, pág. 83. [1]
- Branko Grünbaum , Metamorfosis de polígonos , publicado en El lado más ligero de las matemáticas: Actas de la Conferencia en memoria de Eugène Strens sobre matemáticas recreativas y su historia , (1994)
