Trayectoria terrestre del satélite

Una trayectoria terrestre de un satélite o traza terrestre de un satélite es el camino en la superficie de un planeta directamente debajo de la trayectoria de un satélite . También se conoce como trayectoria suborbital o trayectoria subsatelital , y es la proyección vertical de la órbita del satélite sobre la superficie de la Tierra (o cualquier cuerpo en el que esté orbitando el satélite). ^[1] Una trayectoria terrestre de un satélite puede considerarse como un camino a lo largo de la superficie de la Tierra que traza el movimiento de una línea imaginaria entre el satélite y el centro de la Tierra. En otras palabras, la trayectoria terrestre es el conjunto de puntos en los que el satélite pasará directamente por encima, o cruzará el cenit , en el marco de referencia de un observador terrestre. ^[2]

La trayectoria terrestre de un satélite puede adoptar distintas formas, dependiendo de los valores de los elementos orbitales , parámetros que definen el tamaño, la forma y la orientación de la órbita del satélite, aunque su identificación siempre depende del reconocimiento de la forma física que está en movimiento; ^{[nota 1]} Esto se enfatizó durante la especulación sobre el incidente de Vela , por el cual la identificación de la materia en cuestión fue objeto de numerosas teorías. ^[3]

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (April 2024) (Learn how and when to remove this message)

Por lo general, los satélites tienen una trayectoria terrestre aproximadamente sinusoidal . Se dice que un satélite con una inclinación orbital entre cero y noventa grados está en lo que se denomina una órbita directa o prograda , lo que significa que orbita en la misma dirección que la rotación del planeta. Se dice que un satélite con una inclinación orbital entre 90° y 180° (o, equivalentemente, entre 0° y −90°) está en una órbita retrógrada . ^{[nota 2]}

Un satélite en una órbita directa con un período orbital inferior a un día tenderá a moverse de oeste a este a lo largo de su trayectoria terrestre, lo que se denomina movimiento "directo aparente". Un satélite en una órbita directa con un período orbital superior a un día tenderá a moverse de este a oeste a lo largo de su trayectoria terrestre, lo que se denomina movimiento "retrógrado aparente". Este efecto se produce porque el satélite orbita más lentamente que la velocidad a la que gira la Tierra debajo de él. Cualquier satélite en una verdadera órbita retrógrada siempre se moverá de este a oeste a lo largo de su trayectoria terrestre, independientemente de la longitud de su período orbital.

Debido a que un satélite en una órbita excéntrica se mueve más rápido cerca del perigeo y más lento cerca del apogeo, es posible que un satélite se desplace hacia el este durante una parte de su órbita y hacia el oeste durante otra. Este fenómeno permite que las trayectorias terrestres se crucen entre sí en una sola órbita, como en las órbitas geoestacionarias y de Molniya que se analizan a continuación.

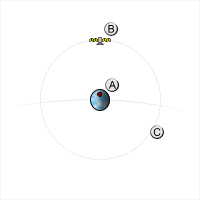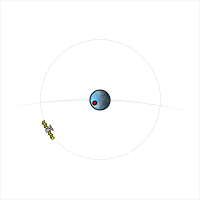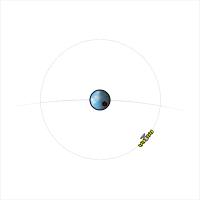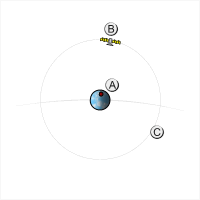
Un satélite cuyo período orbital es una fracción entera de un día (por ejemplo, 24 horas, 12 horas, 8 horas, etc.) seguirá aproximadamente la misma trayectoria terrestre todos los días. Esta trayectoria terrestre se desplaza hacia el este o el oeste según la longitud del nodo ascendente , que puede variar con el tiempo debido a perturbaciones de la órbita. Si el período del satélite es ligeramente más largo que una fracción entera de un día, la trayectoria terrestre se desplazará hacia el oeste con el tiempo; si es ligeramente más corto, la trayectoria terrestre se desplazará hacia el este. ^{[2] [4]}

A medida que el período orbital de un satélite aumenta, acercándose al período de rotación de la Tierra (en otras palabras, a medida que su velocidad orbital promedio disminuye hacia la velocidad de rotación de la Tierra), su trayectoria terrestre sinusoidal se comprimirá longitudinalmente, lo que significa que los "nodos" (los puntos en los que cruza el ecuador ) se acercarán entre sí hasta que, en la órbita geosincrónica, se encuentren directamente uno sobre el otro. Para períodos orbitales más largos que el período de rotación de la Tierra, un aumento en el período orbital corresponde a un estiramiento longitudinal de la trayectoria terrestre (aparentemente retrógrada).

Se dice que un satélite cuyo período orbital es igual al período de rotación de la Tierra se encuentra en una órbita geoestacionaria . Su trayectoria terrestre tendrá forma de "ocho" sobre una ubicación fija en la Tierra, cruzando el ecuador dos veces al día. Seguirá su trayectoria hacia el este cuando se encuentre en la parte de su órbita más cercana al perigeo , y hacia el oeste cuando se encuentre más cerca del apogeo .

Un caso especial de la órbita geoestacionaria, la órbita geoestacionaria , tiene una excentricidad de cero (lo que significa que la órbita es circular) y una inclinación de cero en el sistema de coordenadas centrado y fijo en la Tierra (lo que significa que el plano orbital no está inclinado con respecto al ecuador de la Tierra). La "trayectoria terrestre" en este caso consiste en un único punto en el ecuador de la Tierra, sobre el cual se encuentra el satélite en todo momento. Nótese que el satélite todavía está orbitando la Tierra; su aparente falta de movimiento se debe al hecho de que la Tierra está rotando sobre su propio centro de masas a la misma velocidad que el satélite.

La inclinación orbital es el ángulo que se forma entre el plano de una órbita y el plano ecuatorial de la Tierra. Las latitudes geográficas cubiertas por la trayectoria terrestre oscilarán entre –i y i , donde i es la inclinación orbital. ^[4] En otras palabras, cuanto mayor sea la inclinación de la órbita de un satélite, más al norte y al sur pasará su trayectoria terrestre. Se dice que un satélite con una inclinación de exactamente 90° está en una órbita polar , lo que significa que pasa sobre los polos norte y sur de la Tierra .

Los sitios de lanzamiento en latitudes más bajas suelen preferirse en parte por la flexibilidad que permiten en cuanto a la inclinación orbital; la inclinación inicial de una órbita está limitada a ser mayor o igual que la latitud de lanzamiento. Los vehículos lanzados desde Cabo Cañaveral , por ejemplo, tendrán una inclinación orbital inicial de al menos 28°27′, la latitud del sitio de lanzamiento, y para lograr este mínimo se requiere el lanzamiento con un acimut este correcto , lo que puede no ser siempre factible dadas otras restricciones de lanzamiento. En los extremos, un sitio de lanzamiento ubicado en el ecuador puede lanzar directamente en cualquier inclinación deseada, mientras que un sitio de lanzamiento hipotético en el polo norte o sur solo podría lanzar en órbitas polares. (Si bien es posible realizar una maniobra de cambio de inclinación orbital una vez en órbita, dichas maniobras suelen estar entre las más costosas, en términos de combustible, de todas las maniobras orbitales, y generalmente se evitan o minimizan en la medida de lo posible).

Además de permitir una gama más amplia de inclinaciones orbitales iniciales, los sitios de lanzamiento en latitudes bajas ofrecen la ventaja de requerir menos energía para realizar la órbita (al menos para las órbitas progradas, que comprenden la gran mayoría de los lanzamientos), debido a la velocidad inicial proporcionada por la rotación de la Tierra. El deseo de sitios de lanzamiento ecuatoriales, junto con las realidades geopolíticas y logísticas, ha fomentado el desarrollo de plataformas de lanzamiento flotantes, en particular Sea Launch .

Si el argumento del perigeo es cero, lo que significa que el perigeo y el apogeo se encuentran en el plano ecuatorial, entonces la trayectoria terrestre del satélite parecerá la misma por encima y por debajo del ecuador (es decir, exhibirá una simetría rotacional de 180° sobre los nodos orbitales ). Sin embargo, si el argumento del perigeo no es cero, el satélite se comportará de manera diferente en los hemisferios norte y sur. La órbita de Molniya , con un argumento de perigeo cerca de −90°, es un ejemplo de tal caso. En una órbita de Molniya, el apogeo ocurre en una latitud alta (63°), y la órbita es altamente excéntrica ( e = 0,72). Esto hace que el satélite "flote" sobre una región del hemisferio norte durante mucho tiempo, mientras que pasa muy poco tiempo sobre el hemisferio sur. Este fenómeno se conoce como "permanencia en el apogeo" y es deseable para las comunicaciones en regiones de alta latitud. ^[4]

Como las operaciones orbitales suelen ser necesarias para monitorear una ubicación específica en la Tierra, se suelen utilizar órbitas que cubren la misma trayectoria terrestre periódicamente. En la Tierra, estas órbitas se conocen comúnmente como órbitas de repetición terrestre y suelen diseñarse con parámetros de "órbita congelada" para lograr una órbita de repetición de trayectoria terrestre con elementos orbitales estables (que varían mínimamente con el tiempo). ^[5] Estas órbitas utilizan el efecto de precesión nodal para cambiar la órbita de modo que la trayectoria terrestre coincida con la de una órbita anterior, de modo que esto esencialmente equilibre el desfase en la revolución del cuerpo orbitado. La rotación longitudinal después de un cierto período de tiempo de un planeta está dada por:

${\displaystyle \Delta L_{1}=-2\pi {\frac {T}{T_{E}}}}$

dónde

• ${\displaystyle T}$¿Ha transcurrido el tiempo?
• ${\displaystyle T_{E}}$es el tiempo que tarda un cuerpo en orbitar una revolución completa, en el caso de la Tierra un día sideral

El efecto de la precesión nodal se puede cuantificar como:

${\displaystyle \Delta L_{2}=-{\frac {3\pi J_{2}R_{e}^{2}cos(i)}{a^{2}(1-e^{2})^{2}}}}$

dónde

• ${\displaystyle J_{2}}$Es el segundo factor de forma dinámico del cuerpo .
• ${\displaystyle R_{e}}$es el radio del cuerpo
• ${\displaystyle i}$es la inclinación orbital
• ${\displaystyle a}$es el semieje mayor de la órbita
• ${\displaystyle e}$es la excentricidad orbital

Estos dos efectos deben cancelarse después de un número determinado de revoluciones orbitales y días (siderales). Por lo tanto, al equiparar el tiempo transcurrido con el período orbital del satélite y combinar las dos ecuaciones anteriores, se obtiene una ecuación que se cumple para cualquier órbita que sea una órbita repetida:${\displaystyle j}$${\displaystyle k}$

${\displaystyle j\left|\Delta L_{1}+\Delta L_{2}\right|=j\left|-2\pi {\frac {2\pi {\sqrt {\frac {a^{3}}{\mu }}}}{T_{E}}}-{\frac {3\pi J_{2}R_{e}^{2}cos(i)}{a^{2}(1-e^{2})^{2}}}\right|=k2\pi }$

dónde

• ${\displaystyle \mu }$es el parámetro gravitacional estándar para el cuerpo en órbita
• ${\displaystyle j}$es el número de revoluciones orbitales después de las cuales se cubre la misma trayectoria terrestre
• ${\displaystyle k}$es el número de días siderales después de los cuales se recorre la misma trayectoria terrestre

• Curso (navegación)
• Estación de seguimiento terrestre
• Pase (vuelo espacial) , el período en el que una nave espacial es visible por encima del horizonte local.
• Periodo de revisita del satélite , tiempo transcurrido entre observaciones del mismo punto de la Tierra por un satélite.
• Observación de satélites , como pasatiempo
• Punto subsolar
• Terminador (solar) , la línea móvil que separa el lado diurno iluminado y el lado nocturno oscuro de un cuerpo planetario.

• Lyle, S. y Capderou, Michel (2006) Satélites: órbitas y misiones Springer ISBN 9782287274695 pp 175–264 

• Rastreador satelital en eoPortal.org
• es:satview.org
• cielos-arriba.com
• https://isstracker.pl Rastreador de la Estación Espacial Internacional
• Seguimiento terrestre del satélite, GPS BII-10 en Wayback Machine (archivado el 30 de septiembre de 2020) Satélites pequeños (código de software)
• infosatélites.com
• es.n2yo.com