Orientabilidad

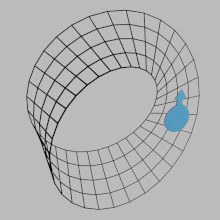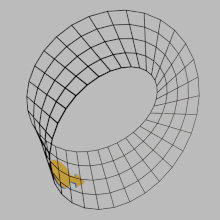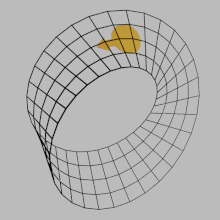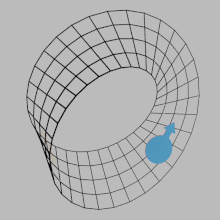
En matemáticas , la orientabilidad es una propiedad de algunos espacios topológicos , como los espacios vectoriales reales , los espacios euclidianos , las superficies y, de manera más general, las variedades , que permite una definición consistente de "sentido horario" y "sentido antihorario". ^[1] Un espacio es orientable si existe una definición consistente de este tipo. En este caso, hay dos definiciones posibles y una elección entre ellas es una orientación del espacio. Los espacios vectoriales reales, los espacios euclidianos y las esferas son orientables. Un espacio no es orientable si "sentido horario" se cambia a "sentido antihorario" después de pasar por algunos bucles en él y volver al punto de partida. Esto significa que una forma geométrica , como, que se mueve continuamente a lo largo de dicho bucle se transforma en su propia imagen especular. Una banda de Möbius es un ejemplo de espacio no orientable.

Se pueden dar varias formulaciones equivalentes de orientabilidad, dependiendo de la aplicación deseada y el nivel de generalidad. Las formulaciones aplicables a variedades topológicas generales a menudo emplean métodos de teoría de homología , mientras que para variedades diferenciables hay más estructura presente, lo que permite una formulación en términos de formas diferenciales . Una generalización de la noción de orientabilidad de un espacio es la de orientabilidad de una familia de espacios parametrizados por algún otro espacio (un haz de fibras ) para el cual se debe seleccionar una orientación en cada uno de los espacios que varía continuamente con respecto a los cambios en los valores de los parámetros.

Una superficie S en el espacio euclidiano R ³ es orientable si una figura bidimensional quiral (por ejemplo,) no se puede mover alrededor de la superficie y volver a donde comenzó para que parezca su propia imagen reflejada (). De lo contrario, la superficie no es orientable . Una superficie abstracta (es decir, una variedad bidimensional ) es orientable si se puede definir un concepto consistente de rotación en el sentido de las agujas del reloj sobre la superficie de manera continua. Es decir, un bucle que gira en un sentido sobre la superficie nunca se puede deformar de manera continua (sin superponerse) en un bucle que gira en el sentido opuesto. Esto resulta ser equivalente a la pregunta de si la superficie no contiene ningún subconjunto que sea homeomorfo a la banda de Möbius . Por lo tanto, para las superficies, la banda de Möbius puede considerarse la fuente de toda no orientabilidad.

En el caso de una superficie orientable, una elección consistente de "sentido horario" (en oposición a sentido antihorario) se denomina orientación y la superficie se denomina orientada . En el caso de superficies insertas en el espacio euclidiano, una orientación se especifica mediante la elección de una normal a la superficie que varía continuamente n en cada punto. Si existe tal normal, siempre hay dos formas de seleccionarla: n o − n . En términos más generales, una superficie orientable admite exactamente dos orientaciones y la distinción entre una superficie orientada y una superficie orientable es sutil y frecuentemente borrosa. Una superficie orientable es una superficie abstracta que admite una orientación, mientras que una superficie orientada es una superficie que es orientable de manera abstracta y tiene el dato adicional de una elección de una de las dos orientaciones posibles.

La mayoría de las superficies que encontramos en el mundo físico son orientables. Las esferas , los planos y los toros son orientables, por ejemplo. Pero las bandas de Möbius , los planos proyectivos reales y las botellas de Klein no son orientables. Todos ellos, tal como se visualizan en tres dimensiones, tienen un solo lado. El plano proyectivo real y la botella de Klein no se pueden incrustar en R ³ , solo sumergir con intersecciones agradables.

Tenga en cuenta que, localmente, una superficie incrustada siempre tiene dos lados, por lo que una hormiga miope que se arrastra sobre una superficie de un solo lado pensaría que hay un "otro lado". La esencia de la unilateralidad es que la hormiga puede arrastrarse de un lado de la superficie al "otro" sin atravesar la superficie ni saltar por un borde, sino simplemente arrastrándose lo suficiente.

En general, la propiedad de ser orientable no es equivalente a ser bilateral; sin embargo, esto se cumple cuando el espacio ambiente (como R ³ arriba) es orientable. Por ejemplo, un toro incrustado en

${\displaystyle K^{2}\times S^{1}}$

puede ser de un solo lado y una botella de Klein en el mismo espacio puede ser de dos lados; aquí se refiere a la botella de Klein.$Estilo de visualización K^{2}}$

Toda superficie tiene una triangulación : una descomposición en triángulos de modo que cada arista de un triángulo esté pegada a, como máximo, otra arista. Cada triángulo se orienta eligiendo una dirección alrededor del perímetro del triángulo, asociando una dirección a cada arista del triángulo. Si esto se hace de tal manera que, al pegarse entre sí, las aristas vecinas apunten en la dirección opuesta, entonces esto determina una orientación de la superficie. Tal elección solo es posible si la superficie es orientable, y en este caso hay exactamente dos orientaciones diferentes.

Si la figurase puede posicionar consistentemente en todos los puntos de la superficie sin convertirse en su imagen especular, entonces esto inducirá una orientación en el sentido anterior en cada uno de los triángulos de la triangulación seleccionando la dirección de cada uno de los triángulos en función del orden rojo-verde-azul de colores de cualquiera de las figuras en el interior del triángulo.

Este enfoque se generaliza a cualquier variedad n que tenga una triangulación. Sin embargo, algunas variedades 4 no tienen una triangulación y, en general, para n > 4, algunas variedades n tienen triangulaciones que no son equivalentes.

Si H ₁ ( S ) denota el primer grupo de homología de una superficie cerrada S , entonces S es orientable si y solo si H ₁ ( S ) tiene un subgrupo de torsión trivial . Más precisamente, si S es orientable entonces H ₁ ( S ) es un grupo abeliano libre , y si no, entonces H ₁ ( S ) = F + Z /2 Z donde F es abeliano libre, y el factor Z /2 Z es generado por la curva media en una banda de Möbius incrustada en S .

Sea M una variedad topológica n conexa . Hay varias definiciones posibles de lo que significa que M sea orientable. Algunas de estas definiciones requieren que M tenga una estructura adicional, como ser diferenciable. Ocasionalmente, n = 0 debe convertirse en un caso especial. Cuando más de una de estas definiciones se aplica a M , entonces M es orientable bajo una definición si y solo si es orientable bajo las otras. ^{[2] [3]}

Las definiciones más intuitivas requieren que M sea una variedad diferenciable. Esto significa que las funciones de transición en el atlas de M son funciones C ¹ . Una función de este tipo admite un determinante jacobiano . Cuando el determinante jacobiano es positivo, se dice que la función de transición preserva la orientación . Un atlas orientado en M es un atlas para el cual todas las funciones de transición preservan la orientación. M es orientable si admite un atlas orientado. Cuando n > 0 , una orientación de M es un atlas orientado maximal. (Cuando n = 0 , una orientación de M es una función M → {±1} .)

La orientabilidad y las orientaciones también se pueden expresar en términos del fibrado tangente. El fibrado tangente es un fibrado vectorial , por lo que es un fibrado fibroso con grupo estructural GL( n , R ) . Es decir, las funciones de transición de la variedad inducen funciones de transición en el fibrado tangente que son transformaciones lineales a lo largo de la fibra. Si el grupo estructural se puede reducir al grupo GL ⁺ ( n , R ) de matrices determinantes positivas, o equivalentemente si existe un atlas cuyas funciones de transición determinan una transformación lineal que preserva la orientación en cada espacio tangente, entonces la variedad M es orientable. A la inversa, M es orientable si y solo si el grupo estructural del fibrado tangente se puede reducir de esta manera. Se pueden hacer observaciones similares para el fibrado de marco.

Otra forma de definir orientaciones en una variedad diferenciable es a través de formas de volumen . Una forma de volumen es una sección que no desaparece en ninguna parte ω de ⋀ ⁿ T ^∗ M , la potencia exterior superior del fibrado cotangente de M . Por ejemplo, R ⁿ tiene una forma de volumen estándar dada por dx ¹ ∧ ⋯ ∧ dx ⁿ . Dada una forma de volumen en M , la colección de todos los gráficos U → R ⁿ para los cuales la forma de volumen estándar retrocede a un múltiplo positivo de ω es un atlas orientado. La existencia de una forma de volumen es, por lo tanto, equivalente a la orientabilidad de la variedad.

Las formas de volumen y los vectores tangentes se pueden combinar para dar otra descripción de la orientabilidad. Si X ₁ , …, X _n es una base de vectores tangentes en un punto p , entonces se dice que la base es dextrógira si ω( X ₁ , …, X _n ) > 0 . Una función de transición preserva la orientación si y solo si envía bases dextrógiras a bases dextrógiras. La existencia de una forma de volumen implica una reducción del grupo estructural del fibrado tangente o del fibrado de marco a GL ⁺ ( n , R ) . Como antes, esto implica la orientabilidad de M . A la inversa, si M es orientable, entonces las formas de volumen locales se pueden unir para crear una forma de volumen global, siendo la orientabilidad necesaria para asegurar que la forma global no desaparezca en ninguna parte.

En el centro de todas las definiciones anteriores de orientabilidad de una variedad diferenciable se encuentra la noción de una función de transición que preserva la orientación. Esto plantea la cuestión de qué es exactamente lo que preservan dichas funciones de transición. No pueden preservar una orientación de la variedad porque una orientación de la variedad es un atlas, y no tiene sentido decir que una función de transición preserva o no preserva un atlas del que es miembro.

Esta cuestión se puede resolver definiendo orientaciones locales. En una variedad unidimensional, una orientación local alrededor de un punto p corresponde a una elección de izquierda y derecha cerca de ese punto. En una variedad bidimensional, corresponde a una elección de sentido horario y antihorario. Estas dos situaciones comparten la característica común de que se describen en términos de comportamiento de dimensión superior cerca de p pero no en p . Para el caso general, sea M una variedad topológica n . Una orientación local de M alrededor de un punto p es una elección de generador del grupo

${\displaystyle H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right).}$

Para ver el significado geométrico de este grupo, elija un gráfico alrededor de p . En ese gráfico hay un entorno de p que es una bola abierta B alrededor del origen O . Por el teorema de escisión , es isomorfo a . La bola B es contráctil, por lo que sus grupos de homología se anulan excepto en el grado cero, y el espacio B \ O es una ( n − 1) -esfera, por lo que sus grupos de homología se anulan excepto en los grados n − 1 y 0 . Un cálculo con la secuencia exacta larga en homología relativa muestra que el grupo de homología anterior es isomorfo a . Por lo tanto, una elección de generador corresponde a una decisión de si, en el gráfico dado, una esfera alrededor de p es positiva o negativa. Una reflexión de R ⁿ a través del origen actúa por negación en , por lo que el significado geométrico de la elección del generador es que distingue los gráficos de sus reflexiones.${\displaystyle H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)}$${\displaystyle H_{n}\left(B,B\setminus \{O\};\mathbf {Z} \right)}$${\displaystyle H_{n-1}\left(S^{n-1};\mathbf {Z} \right)\cong \mathbf {Z} }$${\displaystyle H_{n-1}\left(S^{n-1};\mathbf {Z} \right)}$

En una variedad topológica, una función de transición preserva la orientación si, en cada punto p de su dominio, fija los generadores de . A partir de aquí, las definiciones relevantes son las mismas que en el caso diferenciable. Un atlas orientado es aquel para el cual todas las funciones de transición preservan la orientación, M es orientable si admite un atlas orientado y, cuando n > 0 , una orientación de M es un atlas orientado maximal.${\displaystyle H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)}$

Intuitivamente, una orientación de M debería definir una orientación local única de M en cada punto. Esto se hace preciso al notar que cualquier gráfico en el atlas orientado alrededor de p puede usarse para determinar una esfera alrededor de p , y esta esfera determina un generador de . Además, cualquier otro gráfico alrededor de p está relacionado con el primer gráfico mediante una función de transición que preserva la orientación, y esto implica que los dos gráficos producen el mismo generador, por lo que el generador es único.${\displaystyle H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)}$

También son posibles definiciones puramente homológicas. Suponiendo que M es cerrado y conexo, M es orientable si y sólo si el n- ésimo grupo de homología es isomorfo a los enteros Z. Una orientación de M es una elección del generador α de este grupo. Este generador determina un atlas orientado fijando un generador del grupo cíclico infinito y tomando las cartas orientadas como aquellas para las que α empuja hacia adelante al generador fijo. A la inversa, un atlas orientado determina un generador de este tipo ya que las orientaciones locales compatibles se pueden unir para dar un generador para el grupo de homología . ^[4]${\displaystyle H_{n}(M;\mathbf {Z} )}$${\displaystyle H_{n}(M;\mathbf {Z} )}$${\displaystyle H_{n}(M;\mathbf {Z} )}$

Una variedad M es orientable si y solo si la primera clase de Stiefel–Whitney se anula. En particular, si el primer grupo de cohomología con coeficientes Z /2 es cero, entonces la variedad es orientable. Además, si M es orientable y w ₁ se anula, entonces parametriza las opciones de orientaciones. ^[5] Esta caracterización de la orientabilidad se extiende a la orientabilidad de fibrados vectoriales generales sobre M , no solo del fibrado tangente.${\displaystyle w_{1}(M)\en H^{1}(M;\mathbf {Z} /2)}$${\displaystyle H^{0}(M;\mathbf {Z} /2)}$

Alrededor de cada punto de M hay dos orientaciones locales. Intuitivamente, hay una manera de pasar de una orientación local en un punto p a una orientación local en un punto cercano p ′ : cuando los dos puntos se encuentran en el mismo diagrama de coordenadas U → R ⁿ , ese diagrama de coordenadas define orientaciones locales compatibles en p y p ′ . Por lo tanto, al conjunto de orientaciones locales se le puede dar una topología, y esta topología lo convierte en una variedad.

Más precisamente, sea O el conjunto de todas las orientaciones locales de M . Para topologizar O especificaremos una subbase para su topología. Sea U un subconjunto abierto de M elegido de modo que sea isomorfo a Z . Supongamos que α es un generador de este grupo. Para cada p en U , existe una función de empuje hacia adelante . El codominio de este grupo tiene dos generadores, y α se asigna a uno de ellos. La topología en O se define de modo que${\displaystyle H_{n}(M,M\setminus U;\mathbf {Z} )}$${\displaystyle H_{n}(M,M\setminus U;\mathbf {Z} )\to H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)}$

${\displaystyle \{{\text{Imagen de}}\alpha {\text{ en}}H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)\colon p\in U\}}$

Está abierto.

Existe una función canónica π : O → M que envía una orientación local en p a p . Es claro que cada punto de M tiene precisamente dos preimágenes bajo π . De hecho, π es incluso un homeomorfismo local, porque las preimágenes de los conjuntos abiertos U mencionados anteriormente son homeomorfas a la unión disjunta de dos copias de U . Si M es orientable, entonces M mismo es uno de estos conjuntos abiertos, por lo que O es la unión disjunta de dos copias de M . Sin embargo, si M no es orientable, entonces O es conexo y orientable. La variedad O se llama doble cubierta de orientación .

Si M es una variedad con borde, entonces una orientación de M se define como una orientación de su interior. Tal orientación induce una orientación de ∂ M . De hecho, supongamos que una orientación de M es fija. Sea U → R ⁿ ₊ una carta en un punto de borde de M que, cuando se restringe al interior de M , está en el atlas orientado elegido. La restricción de esta carta a ∂ M es una carta de ∂ M . Tales cartas forman un atlas orientado para ∂ M .

Cuando M es suave, en cada punto p de ∂ M , la restricción del fibrado tangente de M a ∂ M es isomorfa a T _p ∂ M ⊕ R , donde el factor de R se describe por el vector normal que apunta hacia adentro. La orientación de T _p ∂ M se define por la condición de que una base de T _p ∂ M está orientada positivamente si y solo si, cuando se combina con el vector normal que apunta hacia adentro, define una base orientada positivamente de T _p M .

Una noción estrechamente relacionada utiliza la idea de espacio de cobertura . Para una variedad conexa M tome M ^∗ , el conjunto de pares ( x , o) donde x es un punto de M y o es una orientación en x ; aquí suponemos que M es suave, por lo que podemos elegir una orientación en el espacio tangente en un punto o usamos homología singular para definir la orientación. Luego, para cada subconjunto abierto y orientado de M, consideramos el conjunto de pares correspondiente y lo definimos como un conjunto abierto de M ^∗ . Esto le da a M ^∗ una topología y la proyección que envía ( x , o) a x es entonces una función de cobertura 2 a 1. Este espacio de cobertura se llama cobertura doble orientable , ya que es orientable. M ^∗ es conexo si y solo si M no es orientable.

Otra forma de construir esta cubierta es dividir los bucles basados ​​en un punto base en bucles que preservan la orientación o que invierten la orientación. Los bucles que preservan la orientación generan un subgrupo del grupo fundamental que es el grupo completo o el de índice dos. En el último caso (lo que significa que hay un camino que invierte la orientación), el subgrupo corresponde a una doble cubierta conectada; esta cubierta es orientable por construcción. En el primer caso, uno puede simplemente tomar dos copias de M , cada una de las cuales corresponde a una orientación diferente.

Un fibrado vectorial real , que a priori tiene un grupo de estructura GL(n) , se llama orientable cuando el grupo de estructura puede reducirse a , el grupo de matrices con determinante positivo . Para el fibrado tangente , esta reducción siempre es posible si la variedad base subyacente es orientable y, de hecho, esto proporciona una forma conveniente de definir la orientabilidad de una variedad real lisa : una variedad lisa se define como orientable si su fibrado tangente es orientable (como fibrado vectorial). Nótese que, como variedad por derecho propio, el fibrado tangente siempre es orientable, incluso sobre variedades no orientables.$Estilo de visualización GL+(n)$

En la geometría lorentziana , hay dos tipos de orientabilidad: la orientabilidad espacial y la orientabilidad temporal. Estas desempeñan un papel en la estructura causal del espacio-tiempo. ^[6] En el contexto de la relatividad general , una variedad espacio-temporal es orientable espacialmente si, siempre que dos observadores diestros se dirigen en naves espaciales comenzando en el mismo punto del espacio-tiempo, y luego se encuentran nuevamente en otro punto, permanecen diestros uno con respecto al otro. Si un espacio-tiempo es orientable en el tiempo, entonces los dos observadores siempre estarán de acuerdo en la dirección del tiempo en ambos puntos de su encuentro. De hecho, un espacio-tiempo es orientable en el tiempo si y solo si dos observadores pueden estar de acuerdo en cuál de los dos encuentros precedió al otro. ^[7]

Formalmente, el grupo pseudoortogonal O( p , q ) tiene un par de caracteres : el carácter de orientación espacial σ ₊ y el carácter de orientación temporal σ ₋ ,

${\displaystyle \sigma _{\pm }:\nombre del operador {O} (p,q)\to \{-1,+1\}.}$

Su producto σ = σ ₊ σ ₋ es el determinante, que da el carácter de orientación. Una orientación espacial de una variedad pseudoriemanniana se identifica con una sección del fibrado asociado.

${\displaystyle \operatorname {O} (M)\times _{\sigma _{+}}\{-1,+1\}}$

donde O( M ) es el fibrado de marcos pseudo-ortogonales. De manera similar, una orientación temporal es una sección del fibrado asociado.

${\displaystyle \operatorname {O} (M)\times _{\sigma _{-}}\{-1,+1\}.}$

• Orientación de la curva
• Gavilla de orientación

• Orientación de colectores en el Atlas de colectores.
• Cobertura de orientación en el Atlas Manifold.
• Orientación de variedades en teorías de cohomología generalizada en el Atlas de variedades.
• Artículo de la Enciclopedia de Matemáticas sobre Orientación.