Modulación por desplazamiento de fase

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (October 2022) (Learn how and when to remove this message) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (October 2022) (Learn how and when to remove this message) This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (March 2024) (Learn how and when to remove this message) (Learn how and when to remove this message)

Passband modulation
Analog modulation
AM FM PM QAM SM SSB
Digital modulation
ASK APSK CPM FSK MFSK MSK OOK PPM PSK QAM SC-FDE TCM TC-PAM WDM
Hierarchical modulation
QAM WDM
Spread spectrum
CSS DSSS FHSS THSS
See also
Capacity-approaching codes Demodulation Line coding Modem AnM PoM PAM PCM PDM PWM ΔΣM OFDM FDM Multiplexing
v t e

La modulación por desplazamiento de fase ( PSK ) es un proceso de modulación digital que transmite datos modificando (modulando) la fase de una onda portadora de frecuencia constante . La modulación se logra variando las entradas de seno y coseno en un momento preciso. Se utiliza ampliamente para redes LAN inalámbricas , RFID y comunicación Bluetooth .

Cualquier esquema de modulación digital utiliza un número finito de señales distintas para representar datos digitales. PSK utiliza un número finito de fases, a cada una de las cuales se le asigna un patrón único de dígitos binarios . Por lo general, cada fase codifica un número igual de bits. Cada patrón de bits forma el símbolo que representa la fase particular. El demodulador , que está diseñado específicamente para el conjunto de símbolos utilizado por el modulador, determina la fase de la señal recibida y la asigna de nuevo al símbolo que representa, recuperando así los datos originales. Esto requiere que el receptor pueda comparar la fase de la señal recibida con una señal de referencia; un sistema de este tipo se denomina coherente (y se lo conoce como CPSK).

CPSK requiere un demodulador complicado, porque debe extraer la onda de referencia de la señal recibida y realizar un seguimiento de ella, para comparar cada muestra. Alternativamente, el cambio de fase de cada símbolo enviado se puede medir con respecto a la fase del símbolo anterior enviado. Debido a que los símbolos se codifican en la diferencia de fase entre muestras sucesivas, esto se llama modulación por desplazamiento de fase diferencial (DPSK) . DPSK puede ser significativamente más simple de implementar que PSK ordinario, ya que es un esquema "no coherente", es decir, no hay necesidad de que el demodulador realice un seguimiento de una onda de referencia. Una desventaja es que tiene más errores de demodulación.

Hay tres clases principales de técnicas de modulación digital utilizadas para la transmisión de datos representados digitalmente :

• Modulación por desplazamiento de amplitud (ASK)
• Modulación por desplazamiento de frecuencia (FSK)
• Modulación por desplazamiento de fase (PSK)

Todos transmiten datos modificando algún aspecto de una señal base, la onda portadora (normalmente una onda sinusoidal ), en respuesta a una señal de datos. En el caso de PSK, se modifica la fase para representar la señal de datos. Existen dos formas fundamentales de utilizar la fase de una señal de esta manera:

• Al considerar la fase en sí misma como la que transmite la información, en cuyo caso el demodulador debe tener una señal de referencia con la cual comparar la fase de la señal recibida; o
• Al considerar el cambio de fase como una transmisión de información, se generan esquemas diferenciales, algunos de los cuales no necesitan un portador de referencia (hasta cierto punto).

Un método conveniente para representar esquemas PSK es en un diagrama de constelación . Este muestra los puntos en el plano complejo donde, en este contexto, los ejes real e imaginario se denominan ejes en fase y en cuadratura respectivamente debido a su separación de 90°. Esta representación en ejes perpendiculares se presta a una implementación sencilla. La amplitud de cada punto a lo largo del eje en fase se utiliza para modular una onda coseno (o seno) y la amplitud a lo largo del eje de cuadratura para modular una onda seno (o coseno). Por convención, en fase modula el coseno y la cuadratura modula el seno.

En PSK, los puntos de constelación elegidos se colocan generalmente con un espaciado angular uniforme alrededor de un círculo . Esto proporciona la máxima separación de fases entre puntos adyacentes y, por lo tanto, la mejor inmunidad a la corrupción. Se colocan en un círculo de modo que todos puedan transmitirse con la misma energía. De esta manera, los módulos de los números complejos que representan serán los mismos y, por lo tanto, también lo serán las amplitudes necesarias para las ondas coseno y seno. Dos ejemplos comunes son la "modulación por desplazamiento de fase binaria" (BPSK), que utiliza dos fases, y la "modulación por desplazamiento de fase en cuadratura" (QPSK), que utiliza cuatro fases, aunque se puede utilizar cualquier número de fases. Dado que los datos que se van a transmitir son generalmente binarios, el esquema PSK suele diseñarse con el número de puntos de constelación siendo una potencia de dos.

BPSK (también llamado a veces PRK, modulación por inversión de fase o 2PSK) es la forma más simple de modulación por desplazamiento de fase (PSK). Utiliza dos fases que están separadas por 180° y, por lo tanto, también se puede denominar 2-PSK. No importa particularmente dónde se colocan exactamente los puntos de la constelación, y en esta figura se muestran en el eje real, a 0° y 180°. Por lo tanto, maneja el nivel de ruido o distorsión más alto antes de que el demodulador tome una decisión incorrecta. Eso lo convierte en el más robusto de todos los PSK. Sin embargo, solo puede modular a 1  bit/símbolo (como se ve en la figura) y, por lo tanto, no es adecuado para aplicaciones de alta velocidad de datos.

En presencia de un cambio de fase arbitrario introducido por el canal de comunicaciones , el demodulador (véase, por ejemplo, el bucle de Costas ) no puede determinar qué punto de la constelación es cuál. Como resultado, los datos suelen codificarse de forma diferencial antes de la modulación.

BPSK es funcionalmente equivalente a la modulación 2-QAM .

La forma general para BPSK sigue la ecuación:

${\displaystyle s_{n}(t)={\sqrt {\frac {2E_{b}}{T_{b}}}}\cos(2\pi ft+\pi (1-n)),\quad n=0,1.}$

Esto produce dos fases, 0 y π. En la forma específica, los datos binarios se transmiten a menudo con las siguientes señales: ^{[ cita requerida ]}

${\displaystyle s_{0}(t)={\sqrt {\frac {2E_{b}}{T_{b}}}}\cos(2\pi ft+\pi )=-{\sqrt {\frac {2E_{b}}{T_{b}}}}\cos(2\pi ft)}$para binario "0"

${\displaystyle s_{1}(t)={\sqrt {\frac {2E_{b}}{T_{b}}}}\cos(2\pi ft)}$para binario "1"

donde f es la frecuencia de la banda base.

Por lo tanto, el espacio de señal se puede representar mediante la función base única

${\displaystyle \phi (t)={\sqrt {\frac {2}{T_{b}}}}\cos(2\pi ft)}$

donde 1 está representado por y 0 está representado por . Esta asignación es arbitraria.${\displaystyle {\sqrt {E_{b}}}\phi (t)}$${\displaystyle -{\sqrt {E_{b}}}\phi (t)}$

El uso de esta función base se muestra al final de la siguiente sección en un diagrama de sincronización de señal. La señal superior es una onda coseno modulada por BPSK que produciría el modulador BPSK. El flujo de bits que causa esta salida se muestra sobre la señal (las otras partes de esta figura son relevantes solo para QPSK). Después de la modulación, la señal de banda base se moverá a la banda de alta frecuencia multiplicando .${\displaystyle \cos(2\pi f_{c}t)}$

La tasa de error de bits (BER) de BPSK bajo ruido gaussiano blanco aditivo (AWGN) se puede calcular como: ^[1]

${\displaystyle P_{b}=Q\left({\sqrt {\frac {2E_{b}}{N_{0}}}}\right)}$o${\displaystyle P_{e}={\frac {1}{2}}\operatorname {erfc} \left({\sqrt {\frac {E_{b}}{N_{0}}}}\right)}$

Dado que solo hay un bit por símbolo, esta es también la tasa de error de símbolo.

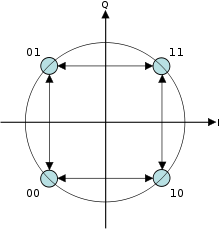
A veces, esto se conoce como PSK cuatrifásico , 4-PSK o 4 - QAM . (Aunque los conceptos básicos de QPSK y 4-QAM son diferentes, las ondas de radio moduladas resultantes son exactamente las mismas). QPSK utiliza cuatro puntos en el diagrama de constelación, equiespaciados alrededor de un círculo. Con cuatro fases, QPSK puede codificar dos bits por símbolo, que se muestra en el diagrama con codificación Gray para minimizar la tasa de error de bit (BER), a veces malinterpretada como el doble de la BER de BPSK.

El análisis matemático muestra que QPSK puede utilizarse para duplicar la velocidad de datos en comparación con un sistema BPSK manteniendo el mismo ancho de banda de la señal, o para mantener la velocidad de datos de BPSK pero reduciendo a la mitad el ancho de banda necesario. En este último caso, la BER de QPSK es exactamente la misma que la de BPSK, y creer lo contrario es una confusión común al considerar o describir QPSK. La portadora transmitida puede sufrir numerosos cambios de fase.

Dado que los canales de comunicación por radio son asignados por agencias como la Comisión Federal de Comunicaciones, que otorga un ancho de banda (máximo) prescrito, la ventaja de QPSK sobre BPSK se hace evidente: QPSK transmite el doble de velocidad de datos en un ancho de banda determinado en comparación con BPSK, con la misma BER. La penalización de ingeniería que se paga es que los transmisores y receptores QPSK son más complicados que los de BPSK. Sin embargo, con la tecnología electrónica moderna , la penalización en términos de costo es muy moderada.

Al igual que con BPSK, existen problemas de ambigüedad de fase en el extremo receptor y, en la práctica, a menudo se utiliza QPSK codificado diferencialmente.

La implementación de QPSK es más general que la de BPSK y también indica la implementación de PSK de orden superior. Escribiendo los símbolos en el diagrama de constelación en términos de las ondas seno y coseno utilizadas para transmitirlos:

${\displaystyle s_{n}(t)={\sqrt {\frac {2E_{s}}{T_{s}}}}\cos \left(2\pi f_{c}t+(2n-1){\frac {\pi }{4}}\right),\quad n=1,2,3,4.}$

Esto produce las cuatro fases π/4, 3π/4, 5π/4 y 7π/4 según sea necesario.

Esto da como resultado un espacio de señal bidimensional con funciones de base unitaria.

${\displaystyle {\begin{aligned}\phi _{1}(t)&={\sqrt {\frac {2}{T_{s}}}}\cos \left(2\pi f_{c}t\right)\\\phi _{2}(t)&={\sqrt {\frac {2}{T_{s}}}}\sin \left(2\pi f_{c}t\right)\end{aligned}}}$

La primera función base se utiliza como componente en fase de la señal y la segunda como componente en cuadratura de la señal.

Por lo tanto, la constelación de señales consta de los 4 puntos del espacio de señales.

${\displaystyle {\begin{pmatrix}\pm {\sqrt {\frac {E_{s}}{2}}}&\pm {\sqrt {\frac {E_{s}}{2}}}\end{pmatrix}}.}$

Los factores de 1/2 indican que la potencia total se divide equitativamente entre los dos portadores.

La comparación de estas funciones base con las de BPSK muestra claramente cómo se puede considerar a QPSK como dos señales BPSK independientes. Nótese que los puntos del espacio de señal para BPSK no necesitan dividir la energía del símbolo (bit) entre las dos portadoras en el esquema que se muestra en el diagrama de constelación de BPSK.

Los sistemas QPSK se pueden implementar de varias maneras. A continuación se muestra una ilustración de los componentes principales de la estructura del transmisor y del receptor.

Aunque la QPSK puede considerarse una modulación cuaternaria, es más fácil verla como dos portadoras en cuadratura moduladas independientemente. Con esta interpretación, los bits pares (o impares) se utilizan para modular el componente en fase de la portadora, mientras que los bits impares (o pares) se utilizan para modular el componente en cuadratura de fase de la portadora. La BPSK se utiliza en ambas portadoras y se pueden demodular de forma independiente.

Como resultado, la probabilidad de error de bit para QPSK es la misma que para BPSK:

${\displaystyle P_{b}=Q\left({\sqrt {\frac {2E_{b}}{N_{0}}}}\right)}$

Sin embargo, para lograr la misma probabilidad de error de bit que BPSK, QPSK utiliza el doble de potencia (ya que se transmiten dos bits simultáneamente).

La tasa de error de símbolo viene dada por:

${\displaystyle {\begin{aligned}P_{s}&=1-\left(1-P_{b}\right)^{2}\\&=2Q\left({\sqrt {\frac {E_{s}}{N_{0}}}}\right)-\left[Q\left({\sqrt {\frac {E_{s}}{N_{0}}}}\right)\right]^{2}.\end{aligned}}}$

Si la relación señal-ruido es alta (como es necesario para los sistemas QPSK prácticos), la probabilidad de error de símbolo puede aproximarse:

${\displaystyle P_{s}\approx 2Q\left({\sqrt {\frac {E_{s}}{N_{0}}}}\right)=\operatorname {erfc} \left({\sqrt {\frac {E_{s}}{2N_{0}}}}\right)=\operatorname {erfc} \left({\sqrt {\frac {E_{b}}{N_{0}}}}\right)}$

La señal modulada se muestra a continuación para un segmento corto de un flujo de datos binario aleatorio. Las dos ondas portadoras son una onda coseno y una onda seno, como se indica en el análisis del espacio de señal anterior. Aquí, los bits impares se han asignado al componente en fase y los bits pares al componente en cuadratura (tomando el primer bit como número 1). La señal total (la suma de los dos componentes) se muestra en la parte inferior. Se pueden ver saltos de fase a medida que la PSK cambia la fase de cada componente al comienzo de cada período de bit. La forma de onda superior por sí sola coincide con la descripción dada para BPSK anterior.

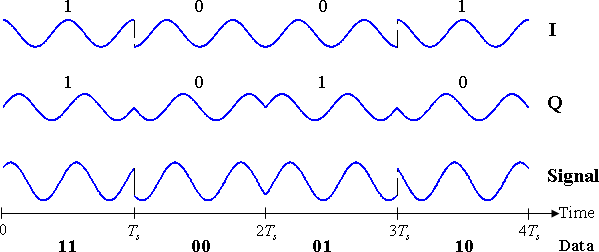
Los datos binarios que transmite esta forma de onda son: 11000110 .

• Los bits impares, resaltados aquí, contribuyen al componente en fase: 1 1 0 0 0 1 1 0
• Los bits pares, resaltados aquí, contribuyen al componente de cuadratura de fase: 1 1 0 0 0 1 1 0

La modulación por desplazamiento de fase en cuadratura con desplazamiento ( OQPSK ) es una variante de la modulación por desplazamiento de fase que utiliza cuatro valores diferentes de la fase para transmitir. A veces se denomina modulación por desplazamiento de fase en cuadratura escalonada ( SQPSK ).

Tomar cuatro valores de la fase (dos bits ) a la vez para construir un símbolo QPSK puede permitir que la fase de la señal salte hasta 180° a la vez. Cuando la señal se filtra con un filtro de paso bajo (como es típico en un transmisor), estos cambios de fase resultan en grandes fluctuaciones de amplitud, una cualidad indeseable en los sistemas de comunicación. Al compensar la sincronización de los bits pares e impares en un período de bit, o la mitad de un período de símbolo, los componentes en fase y en cuadratura nunca cambiarán al mismo tiempo. En el diagrama de constelación que se muestra a la derecha, se puede ver que esto limitará el cambio de fase a no más de 90° a la vez. Esto produce fluctuaciones de amplitud mucho menores que QPSK sin compensación y, a veces, se prefiere en la práctica.

La imagen de la derecha muestra la diferencia en el comportamiento de la fase entre QPSK ordinario y OQPSK. Se puede ver que en el primer gráfico la fase puede cambiar 180° de una sola vez, mientras que en OQPSK los cambios nunca son mayores de 90°.

A continuación se muestra la señal modulada correspondiente a un segmento corto de un flujo de datos binario aleatorio. Observe el desfase de medio período de símbolo entre las dos ondas componentes. Los cambios de fase repentinos se producen aproximadamente con el doble de frecuencia que en el caso de OQPSK (ya que las señales ya no cambian juntas), pero son menos graves. En otras palabras, la magnitud de los saltos es menor en OQPSK en comparación con QPSK.

El QPSK con desplazamiento en forma libre de licencia (SOQPSK) es interoperable con el QPSK patentado por Feher ( FQPSK ), en el sentido de que un detector QPSK con desplazamiento de integración y volcado produce la misma salida sin importar qué tipo de transmisor se utilice. ^[2]

Estas modulaciones dan forma cuidadosamente a las formas de onda I y Q de modo que cambian de manera muy suave y la señal se mantiene en amplitud constante incluso durante las transiciones de señal. (En lugar de viajar instantáneamente de un símbolo a otro, o incluso de manera lineal, viaja suavemente alrededor del círculo de amplitud constante de un símbolo al siguiente). La modulación SOQPSK se puede representar como un híbrido de QPSK y MSK : SOQPSK tiene la misma constelación de señales que QPSK, sin embargo, la fase de SOQPSK siempre es estacionaria. ^{[3] [4]}

La descripción estándar de SOQPSK-TG implica símbolos ternarios . ^[5] SOQPSK es uno de los esquemas de modulación más extendidos en aplicación a las comunicaciones por satélite LEO . ^[6]

Esta variante de QPSK utiliza dos constelaciones idénticas que están rotadas 45° ( radianes, de ahí el nombre) una con respecto a la otra. Por lo general, se utilizan los símbolos pares o impares para seleccionar puntos de una de las constelaciones y los otros símbolos seleccionan puntos de la otra constelación. Esto también reduce los cambios de fase desde un máximo de 180°, pero solo hasta un máximo de 135° y, por lo tanto, las fluctuaciones de amplitud de -QPSK están entre OQPSK y QPSK sin desplazamiento.${\displaystyle \pi /4}$${\displaystyle \pi /4}$

Una propiedad que posee este esquema de modulación es que si la señal modulada se representa en el dominio complejo, las transiciones entre símbolos nunca pasan por 0. En otras palabras, la señal no pasa por el origen. Esto reduce el rango dinámico de fluctuaciones en la señal, lo cual es deseable cuando se diseñan señales de comunicaciones.

Por otra parte, -QPSK se presta a una fácil demodulación y ha sido adoptado para su uso, por ejemplo, en sistemas de telefonía celular TDMA .${\displaystyle \pi /4}$

La señal modulada se muestra a continuación para un segmento corto de un flujo de datos binario aleatorio. La construcción es la misma que la anterior para QPSK ordinaria. Los símbolos sucesivos se toman de las dos constelaciones que se muestran en el diagrama. Por lo tanto, el primer símbolo (1 1) se toma de la constelación "azul" y el segundo símbolo (0 0) se toma de la constelación "verde". Nótese que las magnitudes de las dos ondas componentes cambian a medida que cambian entre constelaciones, pero la magnitud de la señal total permanece constante ( envolvente constante ). Los cambios de fase están entre los de los dos diagramas de tiempo anteriores.

Modulación por desplazamiento de fase en cuadratura de polarización dual (DPQPSK) o QPSK de polarización dual : implica la multiplexación de polarización de dos señales QPSK diferentes, mejorando así la eficiencia espectral en un factor de 2. Esta es una alternativa rentable al uso de 16-PSK, en lugar de QPSK para duplicar la eficiencia espectral.

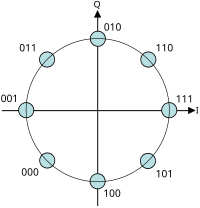
Se puede utilizar cualquier número de fases para construir una constelación PSK, pero la constelación PSK de orden más alto que se utiliza es la 8-PSK. Con más de 8 fases, la tasa de error se vuelve demasiado alta y hay modulaciones mejores, aunque más complejas, disponibles, como la modulación de amplitud en cuadratura (QAM). Aunque se puede utilizar cualquier número de fases, el hecho de que la constelación deba tratar normalmente con datos binarios significa que el número de símbolos suele ser una potencia de 2 para permitir un número entero de bits por símbolo.

Para la M-PSK general no existe una expresión simple para la probabilidad de error de símbolo si . Desafortunadamente, solo se puede obtener a partir de${\displaystyle M>4}$

${\displaystyle P_{s}=1-\int _{-\pi /M}^{\pi /M}p_{\theta _{r}}\left(\theta _{r}\right)d\theta _{r},}$

dónde

${\displaystyle {\begin{aligned}p_{\theta _{r}}\left(\theta _{r}\right)&={\frac {1}{2\pi }}e^{-2\gamma _{s}\sin ^{2}\theta _{r}}\int _{0}^{\infty }Ve^{-{\frac {1}{2}}\left(V-2{\sqrt {\gamma _{s}}}\cos \theta _{r}\right)^{2}}\,dV,\\V&={\sqrt {r_{1}^{2}+r_{2}^{2}}},\\\theta _{r}&=\tan ^{-1}\left({\frac {r_{2}}{r_{1}}}\right),\\\gamma _{s}&={\frac {E_{s}}{N_{0}}}\end{aligned}}}$

y y son cada una variables aleatorias gaussianas .${\displaystyle r_{1}\sim N\left({\sqrt {E_{s}}},{\frac {1}{2}}N_{0}\right)}$${\displaystyle r_{2}\sim N\left(0,{\frac {1}{2}}N_{0}\right)}$

Esto se puede aproximar para alto y alto mediante:${\displaystyle M}$${\displaystyle E_{b}/N_{0}}$

${\displaystyle P_{s}\approx 2Q\left({\sqrt {2\gamma _{s}}}\sin {\frac {\pi }{M}}\right).}$

La probabilidad de error de bit para -PSK solo se puede determinar con exactitud una vez que se conoce el mapeo de bits. Sin embargo, cuando se utiliza la codificación Gray , el error más probable de un símbolo al siguiente produce solo un único error de bit y${\displaystyle M}$

${\displaystyle P_{b}\approx {\frac {1}{k}}P_{s}.}$

(El uso de la codificación Gray nos permite aproximar la distancia de Lee de los errores como la distancia de Hamming de los errores en el flujo de bits decodificado, lo que es más fácil de implementar en hardware).

El gráfico de la derecha compara las tasas de error de bits de BPSK, QPSK (que son las mismas, como se indicó anteriormente), 8-PSK y 16-PSK. Se observa que las modulaciones de orden superior presentan tasas de error más altas; sin embargo, a cambio ofrecen una tasa de datos brutos más alta.

Los límites de las tasas de error de varios esquemas de modulación digital se pueden calcular con la aplicación del límite de unión a la constelación de señales.

La eficiencia del ancho de banda (o espectral) de los esquemas de modulación M-PSK aumenta con el aumento del orden de modulación M (a diferencia, por ejemplo, de M-FSK ): ^[7]

${\displaystyle \rho ={\frac {\log _{2}M}{2}}\quad [{\text{bits}}/{\text{s}}\cdot {\text{Hz}}]}$

La misma relación es válida para M-QAM . ^[8]

La modulación por desplazamiento de fase diferencial (DPSK) es una forma común de modulación de fase que transmite datos modificando la fase de la onda portadora. Como se mencionó para BPSK y QPSK, existe una ambigüedad de fase si la constelación se rota por algún efecto en el canal de comunicaciones por el que pasa la señal. Este problema se puede superar utilizando los datos para cambiar la fase en lugar de establecerla .

Por ejemplo, en BPSK con codificación diferencial, se puede transmitir un "1" binario sumando 180° a la fase actual y un "0" binario sumando 0° a la fase actual.Otra variante de DPSK es el desplazamiento de fase diferencial simétrico, SDPSK, donde la codificación sería +90° para un "1" y −90° para un "0".

En la codificación diferencial QPSK (DQPSK), los desplazamientos de fase son 0°, 90°, 180°, −90° correspondientes a los datos "00", "01", "11", "10". Este tipo de codificación se puede demodular de la misma manera que para la codificación no diferencial PSK, pero se pueden ignorar las ambigüedades de fase. De este modo, cada símbolo recibido se demodula a uno de los puntos de la constelación y un comparador calcula la diferencia de fase entre esta señal recibida y la anterior. La diferencia codifica los datos como se ha descrito anteriormente. La codificación diferencial simétrica por desplazamiento de fase en cuadratura (SDQPSK) es como la DQPSK, pero la codificación es simétrica y utiliza valores de desplazamiento de fase de −135°, −45°, +45° y +135°.${\displaystyle M}$

La señal modulada se muestra a continuación tanto para DBPSK como para DQPSK, como se describió anteriormente. En la figura, se supone que la señal comienza con fase cero y, por lo tanto, hay un cambio de fase en ambas señales en .${\displaystyle t=0}$

El análisis muestra que la codificación diferencial duplica aproximadamente la tasa de error en comparación con la PSK ordinaria, pero esto puede superarse con solo un pequeño aumento de . Además, este análisis (y los resultados gráficos a continuación) se basan en un sistema en el que la única corrupción es el ruido blanco gaussiano aditivo (AWGN). Sin embargo, también habrá un canal físico entre el transmisor y el receptor en el sistema de comunicación. Este canal, en general, introducirá un cambio de fase desconocido en la señal PSK; en estos casos, los esquemas diferenciales pueden producir una mejor tasa de error que los esquemas ordinarios que se basan en información de fase precisa.${\displaystyle M}$${\displaystyle E_{b}/N_{0}}$

Una de las aplicaciones más populares de DPSK es el estándar Bluetooth donde se implementaron -DQPSK y 8-DPSK.${\displaystyle \pi /4}$

Para una señal que ha sido codificada diferencialmente, existe un método alternativo obvio de demodulación. En lugar de demodular como de costumbre e ignorar la ambigüedad de la fase de la portadora, se compara la fase entre dos símbolos recibidos sucesivos y se utiliza para determinar cuáles deben haber sido los datos. Cuando se utiliza la codificación diferencial de esta manera, el esquema se conoce como modulación por desplazamiento de fase diferencial (DPSK). Obsérvese que esto es sutilmente diferente de la modulación por desplazamiento de fase diferencial, ya que, al recibirse, los símbolos recibidos no se decodifican uno por uno en puntos de la constelación, sino que se comparan directamente entre sí.

Llame al símbolo recibido en el intervalo de tiempo ⁿ y déjelo con fase . Suponga sin pérdida de generalidad que la fase de la onda portadora es cero. Denote el término de ruido blanco gaussiano aditivo (AWGN) como . Entonces${\displaystyle k}$${\displaystyle r_{k}}$${\displaystyle \phi _{k}}$${\displaystyle n_{k}}$

${\displaystyle r_{k}={\sqrt {E_{s}}}e^{j\phi _{k}}+n_{k}.}$

La variable de decisión para el símbolo ⁿ y el símbolo ⁿ es la diferencia de fase entre y . Es decir, si se proyecta sobre , la decisión se toma sobre la fase del número complejo resultante:${\displaystyle k-1}$${\displaystyle k}$${\displaystyle r_{k}}$${\displaystyle r_{k-1}}$${\displaystyle r_{k}}$${\displaystyle r_{k-1}}$

${\displaystyle r_{k}r_{k-1}^{*}=E_{s}e^{j\left(\varphi _{k}-\varphi _{k-1}\right)}+{\sqrt {E_{s}}}e^{j\varphi _{k}}n_{k-1}^{*}+{\sqrt {E_{s}}}e^{-j\varphi _{k-1}}n_{k}+n_{k}n_{k-1}^{*}}$

donde el superíndice * denota conjugación compleja . En ausencia de ruido, la fase de esto es , el desfase entre las dos señales recibidas que se puede utilizar para determinar los datos transmitidos.${\displaystyle \phi _{k}-\phi _{k-1}}$

La probabilidad de error para DPSK es difícil de calcular en general, pero, en el caso de DBPSK es:

${\displaystyle P_{b}={\frac {1}{2}}e^{-{\frac {E_{b}}{N_{0}}}},}$^[9]

que, cuando se evalúa numéricamente, es sólo ligeramente peor que el BPSK ordinario, particularmente en valores más altos.${\displaystyle E_{b}/N_{0}}$

El uso de DPSK evita la necesidad de utilizar esquemas de recuperación de portadora posiblemente complejos para proporcionar una estimación de fase precisa y puede ser una alternativa atractiva al PSK ordinario.

En las comunicaciones ópticas , los datos se pueden modular sobre la fase de un láser de forma diferencial. La modulación consiste en un láser que emite una onda continua y un modulador Mach–Zehnder que recibe datos binarios eléctricos. En el caso de BPSK, el láser transmite el campo sin cambios para el binario '1' y con polaridad inversa para el '0'. El demodulador consiste en un interferómetro de línea de retardo que retrasa un bit, de modo que se pueden comparar dos bits a la vez. En el procesamiento posterior, se utiliza un fotodiodo para transformar el campo óptico en una corriente eléctrica, de modo que la información vuelve a su estado original.

En el gráfico de la derecha se comparan las tasas de error de bits de DBPSK y DQPSK con sus contrapartes no diferenciales. La pérdida por usar DBPSK es lo suficientemente pequeña en comparación con la reducción de complejidad que suele utilizarse en sistemas de comunicaciones que, de otro modo, utilizarían BPSK. Sin embargo, en el caso de DQPSK, la pérdida de rendimiento en comparación con QPSK normal es mayor y el diseñador del sistema debe equilibrar esto con la reducción de complejidad.

En la llamada de intervalo de tiempo, el bit que se va a modular , el bit codificado diferencialmente y la señal modulada resultante . Supongamos que el diagrama de constelación coloca los símbolos en ±1 (que es BPSK). El codificador diferencial produce:${\displaystyle k^{\textrm {th}}}$${\displaystyle b_{k}}$${\displaystyle e_{k}}$${\displaystyle m_{k}(t)}$

${\displaystyle \,e_{k}=e_{k-1}\oplus b_{k}}$

donde indica adición binaria o módulo 2 .${\displaystyle \oplus {}}$

Por lo tanto, solo cambia de estado (de binario "0" a binario "1" o de binario "1" a binario "0") si es un binario "1". De lo contrario, permanece en su estado anterior. Esta es la descripción de BPSK con codificación diferencial que se dio anteriormente.${\displaystyle e_{k}}$${\displaystyle b_{k}}$

La señal recibida se demodula para producir y luego el decodificador diferencial invierte el procedimiento de codificación y produce${\displaystyle e_{k}=\pm 1}$

${\displaystyle b_{k}=e_{k}\oplus e_{k-1},}$

ya que la resta binaria es lo mismo que la suma binaria.

Por lo tanto, si y difieren y si son iguales. Por lo tanto, si ambos y están invertidos , se decodificarán correctamente. Por lo tanto, la ambigüedad de fase de 180° no importa.${\displaystyle b_{k}=1}$${\displaystyle e_{k}}$${\displaystyle e_{k-1}}$${\displaystyle b_{k}=0}$${\displaystyle e_{k}}$${\displaystyle e_{k-1}}$${\displaystyle b_{k}}$

Se pueden diseñar esquemas diferenciales para otras modulaciones PSK siguiendo líneas similares. Las formas de onda para DPSK son las mismas que para la PSK con codificación diferencial indicadas anteriormente, ya que el único cambio entre los dos esquemas se produce en el receptor.

La curva BER de este ejemplo se compara con la BPSK ordinaria de la derecha. Como se mencionó anteriormente, si bien la tasa de error se duplica aproximadamente, el aumento necesario para superarlo es pequeño. Sin embargo, el aumento necesario para superar la modulación diferencial en sistemas codificados es mayor, generalmente alrededor de 3 dB. La degradación del rendimiento es el resultado de una transmisión no coherente; en este caso, se refiere al hecho de que el seguimiento de la fase se ignora por completo.${\displaystyle E_{b}/N_{0}}$${\displaystyle E_{b}/N_{0}}$

Para determinar matemáticamente los índices de error, se necesitarán algunas definiciones:

• ${\displaystyle E_{b}}$, energía por bit
• ${\displaystyle E_{s}=nE_{b}}$, energía por símbolo con n bits
• ${\displaystyle T_{b}}$, duración de bit
• ${\displaystyle T_{s}}$, duración del símbolo
• ${\displaystyle {\frac {1}{2}}N_{0}}$, densidad espectral de potencia de ruido ( W / Hz )
• ${\displaystyle P_{b}}$, probabilidad de error de bit
• ${\displaystyle P_{s}}$, probabilidad de error de símbolo

${\displaystyle Q(x)}$dará la probabilidad de que una sola muestra tomada de un proceso aleatorio con media cero y varianza unitaria Función de densidad de probabilidad gaussiana sea mayor o igual a . Es una forma escalada de la función de error gaussiana complementaria :${\displaystyle x}$

${\displaystyle Q(x)={\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }e^{-{\frac {1}{2}}t^{2}}\,dt={\frac {1}{2}}\operatorname {erfc} \left({\frac {x}{\sqrt {2}}}\right),\ x\geq 0}$.

Las tasas de error que se citan aquí son las del ruido blanco gaussiano aditivo (AWGN). Estas tasas de error son inferiores a las calculadas en canales con desvanecimiento , por lo que constituyen un buen punto de referencia teórico con el que comparar.

Debido a la simplicidad de PSK, particularmente cuando se compara con su competidor, la modulación de amplitud en cuadratura , se utiliza ampliamente en las tecnologías existentes.

El estándar de LAN inalámbrica , IEEE 802.11b-1999 , ^{[10] [11]} utiliza una variedad de PSK diferentes dependiendo de la velocidad de datos requerida. En la velocidad básica de 1 Mbit /s, utiliza DBPSK (BPSK diferencial). Para proporcionar la velocidad extendida de 2 Mbit/s, se utiliza DQPSK. Para alcanzar 5,5 Mbit/s y la velocidad completa de 11 Mbit/s, se emplea QPSK, pero tiene que estar acoplado con codificación de código complementaria . El estándar de LAN inalámbrica de mayor velocidad, IEEE 802.11g-2003 , ^{[10] [12]} tiene ocho velocidades de datos: 6, 9, 12, 18, 24, 36, 48 y 54 Mbit/s. Los modos de 6 y 9 Mbit/s utilizan modulación OFDM donde cada subportadora está modulada BPSK. Los modos de 12 y 18 Mbit/s utilizan OFDM con QPSK. Los cuatro modos más rápidos utilizan OFDM con formas de modulación de amplitud en cuadratura .       

Debido a su simplicidad, BPSK es apropiado para transmisores pasivos de bajo costo y se utiliza en estándares RFID como ISO/IEC 14443 que ha sido adoptado para pasaportes biométricos , tarjetas de crédito como ExpressPay de American Express y muchas otras aplicaciones. ^[13]

Bluetooth 2 utiliza -DQPSK en su tasa más baja (2 Mbit/s) y 8-DPSK en su tasa más alta (3 Mbit/s) cuando el enlace entre los dos dispositivos es lo suficientemente robusto. Bluetooth 1 modula con modulación por desplazamiento mínimo gaussiano , un esquema binario, por lo que cualquiera de las opciones de modulación en la versión 2 producirá una tasa de datos más alta. Una tecnología similar, IEEE 802.15.4 (el estándar inalámbrico utilizado por Zigbee ) también se basa en PSK utilizando dos bandas de frecuencia: 868 MHz y 915 MHz con BPSK y a 2,4 GHz con OQPSK.${\displaystyle \pi /4}$    

Tanto QPSK como 8PSK se utilizan ampliamente en la transmisión por satélite. QPSK todavía se utiliza ampliamente en la transmisión de canales satelitales SD y algunos canales HD. La programación de alta definición se entrega casi exclusivamente en 8PSK debido a las mayores tasas de bits del video HD y el alto costo del ancho de banda satelital. ^[14] El estándar DVB-S2 requiere soporte tanto para QPSK como para 8PSK. Los chipsets utilizados en los nuevos decodificadores satelitales, como la serie 7000 de Broadcom , admiten 8PSK y son compatibles con el estándar anterior. ^[15]

Históricamente, los módems síncronos de banda de voz como Bell 201, 208 y 209 y CCITT V.26, V.27, V.29, V.32 y V.34 usaban PSK. ^[16]

La información mutua de PSK se puede evaluar en ruido gaussiano aditivo mediante la integración numérica de su definición. ^[17] Las curvas de información mutua se saturan hasta el número de bits transportados por cada símbolo en el límite de una relación señal/ruido infinita . Por el contrario, en el límite de relaciones señal/ruido pequeñas, la información mutua se aproxima a la capacidad del canal AWGN , que es la suprema entre todas las opciones posibles de distribuciones estadísticas de símbolos.${\displaystyle E_{s}/N_{0}}$

En valores intermedios de relaciones señal/ruido, la información mutua (MI) se aproxima bien mediante: ^[17]

${\displaystyle {\textrm {MI}}\simeq \log _{2}\left({\sqrt {{\frac {4\pi }{e}}{\frac {E_{s}}{N_{0}}}}}\right).}$

La información mutua de PSK a través del canal AWGN es generalmente menor que la de los formatos de modulación QAM .

Wikimedia Commons tiene medios relacionados con Modulación de fase cuantificada .

• Modulación de portadora con desplazamiento binario
• Codificación diferencial
• Modulación  : para obtener una descripción general de todos los esquemas de modulación
• Modulación de fase (PM): el equivalente analógico de PSK
• Modulación polar
• PSK31
• PSK63

La notación y los resultados teóricos de este artículo se basan en material presentado en las siguientes fuentes:

• Proakis, John G. (1995). Comunicaciones digitales. McGraw Hill. ISBN 0-07-113814-5.
• Couch, Leon W. II (1997). Comunicaciones digitales y analógicas . Prentice-Hall. ISBN 0-13-081223-4.
• Haykin, Simon (1988). Comunicaciones digitales . Wiley. ISBN 0-471-62947-2.