Opción (finanzas)
En finanzas , una opción es un contrato que transmite a su propietario, el tenedor , el derecho, pero no la obligación, de comprar o vender una cantidad específica de un activo o instrumento subyacente a un precio de ejercicio especificado en una fecha específica o antes , dependiendo del estilo de la opción.
Las opciones se adquieren normalmente mediante compra, como forma de compensación o como parte de una transacción financiera compleja. Por lo tanto, también son una forma de activo (o pasivo contingente) y tienen una valoración que puede depender de una relación compleja entre el precio del activo subyacente, el tiempo hasta el vencimiento, la volatilidad del mercado , la tasa de interés libre de riesgo y el precio de ejercicio de la opción.
Las opciones pueden negociarse entre partes privadas en transacciones extrabursátiles (OTC) o pueden negociarse en mercados públicos y en vivo en forma de contratos estandarizados.
Definición y aplicación
Una opción es un contrato que otorga al tenedor el derecho a comprar o vender un activo subyacente o un instrumento financiero a un precio de ejercicio especificado en una fecha determinada o antes de dicha fecha, dependiendo de la forma de la opción. Vender o ejercer una opción antes de su vencimiento generalmente requiere que el comprador elija el contrato al precio acordado. El precio de ejercicio puede establecerse por referencia al precio al contado (precio de mercado) del valor o materia prima subyacente el día en que se emite una opción, o puede fijarse con un descuento o una prima. El emisor tiene la obligación correspondiente de cumplir con la transacción (vender o comprar) si el tenedor "ejerce" la opción. Una opción que transmite al tenedor el derecho a comprar a un precio específico se conoce como call , mientras que una que transmite el derecho a vender a un precio específico se conoce como put .
El emisor puede conceder una opción a un comprador como parte de otra transacción (como una emisión de acciones o como parte de un plan de incentivos para empleados), o el comprador puede pagar una prima al emisor por la opción. Una opción de compra normalmente se ejercería solo cuando el precio de ejercicio sea inferior al valor de mercado del activo subyacente, mientras que una opción de venta normalmente se ejercería solo cuando el precio de ejercicio sea superior al valor de mercado. Cuando se ejerce una opción, el costo para el tenedor de la opción es el precio de ejercicio del activo adquirido más la prima, si la hubiera, pagada al emisor. Si la fecha de vencimiento de la opción pasa sin que se ejerza la opción, la opción vence y el tenedor pierde la prima pagada al emisor. En cualquier caso, la prima es un ingreso para el emisor y, normalmente, una pérdida de capital para el tenedor de la opción.
Un tenedor de una opción puede revender la opción a un tercero en un mercado secundario , ya sea en una transacción extrabursátil o en una bolsa de opciones , dependiendo de la opción. El precio de mercado de una opción de estilo americano normalmente sigue de cerca el de la acción subyacente, siendo la diferencia entre el precio de mercado de la acción y el precio de ejercicio de la opción. El precio de mercado real de la opción puede variar dependiendo de una serie de factores, como un tenedor de opciones importante que necesita vender la opción debido a que se acerca la fecha de vencimiento y no tiene los recursos financieros para ejercer la opción, o un comprador en el mercado que intenta acumular una gran tenencia de opciones. La propiedad de una opción generalmente no otorga al tenedor ningún derecho asociado con el activo subyacente, como derechos de voto o cualquier ingreso del activo subyacente, como un dividendo .
Historia
Usos históricos de las opciones
Los contratos similares a las opciones se han utilizado desde la antigüedad. [1] El primer comprador de opciones conocido fue el matemático y filósofo griego Tales de Mileto . En cierta ocasión, se predijo que la cosecha de aceitunas de la temporada sería mayor de lo habitual y, durante la temporada baja, adquirió el derecho a utilizar varias prensas de aceitunas en la primavera siguiente. Cuando llegó la primavera y la cosecha de aceitunas fue mayor de lo esperado, ejerció sus opciones y luego alquiló las prensas a un precio mucho más alto que el que pagó por su "opción". [2] [3]
El libro Confusión de confusiones de 1688 describe la negociación de " opsies " en la Bolsa de Valores de Ámsterdam (ahora Euronext ), explicando que "solo habrá riesgos limitados para usted, mientras que la ganancia puede superar todas sus imaginaciones y esperanzas". [4]
En Londres, las opciones de venta y de rechazo (calls) se convirtieron en instrumentos comerciales conocidos por primera vez en la década de 1690 durante el reinado de Guillermo y María . [5] Los privilegios eran opciones vendidas en el mercado extrabursátil en los Estados Unidos del siglo XIX, con opciones de venta y de compra sobre acciones ofrecidas por intermediarios especializados. Su precio de ejercicio se fijaba a un precio de mercado redondeado el día o la semana en que se compraba la opción, y la fecha de vencimiento era generalmente tres meses después de la compra. No se negociaban en mercados secundarios.
En el mercado inmobiliario , las opciones de compra se han utilizado durante mucho tiempo para reunir grandes parcelas de tierra de propietarios separados; por ejemplo, un desarrollador paga por el derecho a comprar varias parcelas adyacentes, pero no está obligado a comprar estas parcelas y podría no hacerlo a menos que pueda comprar todas las parcelas de la parcela completa. Además, la compra de bienes inmuebles, como casas, requiere que el comprador pague al vendedor en una cuenta de depósito en garantía un pago en garantía , que ofrece al comprador el derecho a comprar la propiedad en los términos establecidos, incluido el precio de compra. [ cita requerida ]
En la industria cinematográfica, los productores de películas o teatros a menudo compran una opción que otorga el derecho (pero no la obligación) de dramatizar un libro o guión específico.
Las líneas de crédito otorgan al prestatario potencial el derecho (pero no la obligación) de solicitar un préstamo dentro de un período de tiempo específico.
Tradicionalmente, en los contratos de bonos se han incluido muchas opciones, u opciones incorporadas . Por ejemplo, muchos bonos son convertibles en acciones ordinarias a opción del comprador, o pueden ser rescatados (recomprados) a precios específicos a opción del emisor. Los prestatarios hipotecarios tienen desde hace mucho tiempo la opción de pagar el préstamo antes de tiempo, lo que corresponde a una opción de rescate de bonos rescatables.
Opciones sobre acciones modernas
Los contratos de opciones se conocen desde hace décadas. En 1973 se creó la Bolsa de Opciones de Chicago , que estableció un régimen que utilizaba formularios y condiciones estandarizados y negociaba a través de una cámara de compensación garantizada. Desde entonces, la actividad comercial y el interés académico han aumentado.
En la actualidad, muchas opciones se crean en forma estandarizada y se negocian a través de cámaras de compensación en bolsas de opciones reguladas . En cambio, otras opciones extrabursátiles se redactan como contratos bilaterales personalizados entre un único comprador y un único vendedor, uno o ambos de los cuales pueden ser un intermediario o un creador de mercado. Las opciones forman parte de una clase más amplia de instrumentos financieros conocidos como productos derivados o, simplemente, derivados. [6] [7]
Especificaciones del contrato
Una opción financiera es un contrato entre dos contrapartes en el que los términos de la opción se especifican en una hoja de condiciones . Los contratos de opciones pueden ser bastante complicados; sin embargo, como mínimo, suelen contener las siguientes especificaciones: [8]
- si el titular de la opción tiene derecho a comprar (una opción de compra ) o derecho a vender (una opción de venta )
- la cantidad y clase de los activos subyacentes (por ejemplo, 100 acciones de XYZ Co. B)
- el precio de ejercicio , también conocido como precio de ejercicio, que es el precio al que se realizará la transacción subyacente en el momento del ejercicio
- la fecha de vencimiento , o expiración, que es la última fecha en que se puede ejercer la opción
- los términos de liquidación , por ejemplo, si el emisor debe entregar el activo real en el momento del ejercicio, o puede simplemente ofrecer el monto equivalente en efectivo
- los términos por los cuales se cotiza la opción en el mercado para convertir el precio cotizado en la prima real: el monto total pagado por el tenedor al emisor
Comercio de opciones
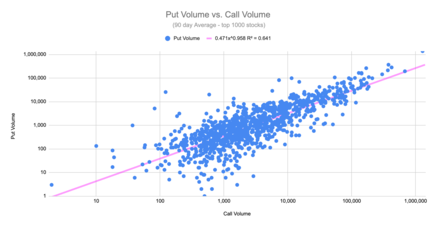
Formas de comercio
Opciones negociadas en bolsa
Las opciones negociadas en bolsa (también llamadas "opciones cotizadas") son una clase de derivados negociados en bolsa . Las opciones negociadas en bolsa tienen contratos estandarizados y se liquidan a través de una cámara de compensación con cumplimiento garantizado por la Corporación de Compensación de Opciones (OCC). Dado que los contratos están estandarizados, a menudo se dispone de modelos de precios precisos. Las opciones negociadas en bolsa incluyen: [9] [10]
- Opciones sobre acciones
- Opciones sobre bonos y otras opciones sobre tasas de interés
- Opciones sobre índices bursátiles o, simplemente, opciones sobre índices
- Opciones sobre contratos de futuros y
- Contrato alcista/bajista con opción de compra
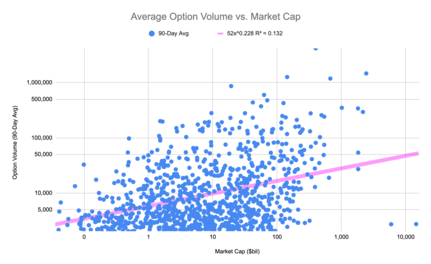
Opciones de venta libre
Las opciones extrabursátiles (OTC, también llamadas "opciones de intermediario") se negocian entre dos partes privadas y no cotizan en una bolsa. Los términos de una opción OTC no tienen restricciones y pueden personalizarse individualmente para satisfacer cualquier necesidad comercial. En general, el emisor de la opción es una institución bien capitalizada (para evitar el riesgo crediticio). Los tipos de opciones que se negocian comúnmente extrabursátiles incluyen:
Al evitar el intercambio, los usuarios de opciones OTC pueden adaptar los términos del contrato de opción a sus necesidades comerciales individuales. Además, las transacciones de opciones OTC generalmente no necesitan ser anunciadas en el mercado y enfrentan pocos o ningún requisito regulatorio. Sin embargo, las contrapartes OTC deben establecer líneas de crédito entre sí y cumplir con los procedimientos de compensación y liquidación de cada una.
Con pocas excepciones, [11] no existen mercados secundarios para las opciones sobre acciones de los empleados . Estas deben ser ejercidas por el beneficiario original o deben dejarse vencer.
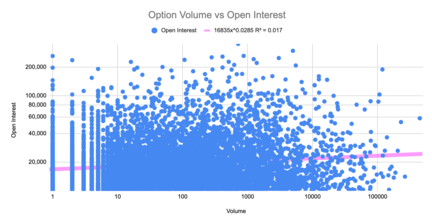
Comercio en bolsa
La forma más común de negociar opciones es a través de contratos de opciones estandarizados listados por varias bolsas de futuros y opciones . [12] Las cotizaciones y los precios se rastrean y se pueden buscar por símbolo de cotización . Al publicar mercados continuos y en vivo para los precios de las opciones, una bolsa permite que partes independientes participen en el descubrimiento de precios y ejecuten transacciones. Como intermediario para ambas partes de la transacción, los beneficios que la bolsa proporciona a la transacción incluyen:
- El cumplimiento del contrato está respaldado por el crédito del exchange, que normalmente tiene la calificación más alta (AAA),
- Las contrapartes permanecen anónimas,
- Aplicación de la regulación del mercado para garantizar la equidad y la transparencia, y
- Mantenimiento de mercados ordenados, especialmente durante condiciones comerciales rápidas.

Oficios básicos (estilo americano)
Estas operaciones se describen desde el punto de vista de un especulador. Si se combinan con otras posiciones, también se pueden utilizar como cobertura . Un contrato de opción en los mercados estadounidenses suele representar 100 acciones del valor subyacente. [13] [14]
Llamada larga

Un operador que espera que el precio de una acción aumente puede comprar una opción de compra para comprar la acción a un precio fijo ( precio de ejercicio ) en una fecha posterior, en lugar de comprar la acción directamente. El desembolso en efectivo de la opción es la prima. El operador no tendría obligación de comprar la acción, sino que solo tiene derecho a hacerlo en la fecha de vencimiento o antes. El riesgo de pérdida se limitaría a la prima pagada, a diferencia de la posible pérdida si la acción se hubiera comprado directamente.
El titular de una opción de compra de estilo americano puede vender la opción en cualquier momento hasta la fecha de vencimiento y consideraría hacerlo cuando el precio al contado de la acción sea superior al precio de ejercicio, especialmente si el titular espera que el precio de la opción baje. Al vender la opción de forma anticipada en esa situación, el operador puede obtener una ganancia inmediata. Alternativamente, el operador puede ejercer la opción (por ejemplo, si no hay un mercado secundario para las opciones) y luego vender la acción, obteniendo una ganancia. Un operador obtendría una ganancia si el precio al contado de las acciones aumenta más que la prima. Por ejemplo, si el precio de ejercicio es 100 y la prima pagada es 10, entonces si el precio al contado de 100 aumenta a solo 110, la transacción es de equilibrio; un aumento en el precio de la acción por encima de 110 produce una ganancia.
Si el precio de la acción al vencimiento es inferior al precio de ejercicio, el tenedor de la opción en ese momento dejará que el contrato de compra expire y perderá únicamente la prima (o el precio pagado en la transferencia).
Posición de venta larga
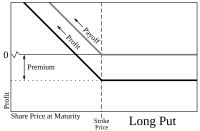
Un operador que espera que el precio de una acción baje puede comprar una opción de venta para vender la acción a un precio fijo (precio de ejercicio) en una fecha posterior. El operador no está obligado a vender la acción, pero tiene el derecho de hacerlo en la fecha de vencimiento o antes. Si el precio de la acción al vencimiento es inferior al precio de ejercicio en una cantidad superior a la prima pagada, el operador obtiene una ganancia. Si el precio de la acción al vencimiento es superior al precio de ejercicio, el operador deja que el contrato de venta expire y pierde solo la prima pagada. En la transacción, la prima también desempeña un papel, ya que mejora el punto de equilibrio. Por ejemplo, si el precio de ejercicio es 100 y la prima pagada es 10, entonces un precio al contado entre 90 y 100 no es rentable. El operador obtiene una ganancia solo si el precio al contado es inferior a 90.
El comerciante que ejerce una opción de venta sobre una acción no necesita ser propietario del activo subyacente, porque la mayoría de las acciones pueden venderse en corto .
Llamada corta

Un operador que espera que el precio de una acción baje puede vender la acción en corto o, en su lugar, vender o "escribir" una opción de compra. El operador que vende una opción de compra tiene la obligación de vender la acción al comprador de la opción de compra a un precio fijo ("precio de ejercicio"). Si el vendedor no posee la acción cuando se ejerce la opción, está obligado a comprar la acción en el mercado al precio de mercado vigente. Si el precio de la acción baja, el vendedor de la opción de compra (escritor de la opción de compra) obtiene una ganancia por el monto de la prima. Si el precio de la acción aumenta por encima del precio de ejercicio en una cantidad mayor que la prima, el vendedor pierde dinero, y la pérdida potencial es ilimitada.
Opción de venta corta

Un operador que espera que el precio de una acción aumente puede comprar la acción o, en su lugar, vender o "escribir" una opción de venta. El operador que vende una opción de venta tiene la obligación de comprar la acción al comprador de la opción de venta a un precio fijo ("precio de ejercicio"). Si el precio de la acción al vencimiento es superior al precio de ejercicio, el vendedor de la opción de venta (escritor de opciones de venta) obtiene una ganancia por el importe de la prima. Si el precio de la acción al vencimiento es inferior al precio de ejercicio en una cantidad superior al importe de la prima, el operador pierde dinero, y la pérdida potencial puede llegar hasta el precio de ejercicio menos la prima. Un índice de referencia para el rendimiento de una posición corta en opciones de venta garantizadas con efectivo es el índice CBOE S&P 500 PutWrite (ticker PUT).
Estrategias de opciones


La combinación de cualquiera de los cuatro tipos básicos de operaciones con opciones (posiblemente con diferentes precios de ejercicio y vencimientos) y los dos tipos básicos de operaciones con acciones (largas y cortas) permite una variedad de estrategias de opciones . Las estrategias simples generalmente combinan solo unas pocas operaciones, mientras que las estrategias más complicadas pueden combinar varias.
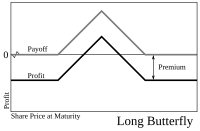
Las estrategias se utilizan a menudo para diseñar un perfil de riesgo particular para los movimientos del valor subyacente. Por ejemplo, comprar un spread mariposa (posición larga en una opción call X1, posición corta en dos opciones call X2 y posición larga en una opción call X3) permite al operador obtener ganancias si el precio de la acción en la fecha de vencimiento está cerca del precio de ejercicio medio, X2, y no expone al operador a una pérdida importante.
Un cóndor es una estrategia similar a un spread mariposa, pero con diferentes precios de ejercicio para las opciones cortas, lo que ofrece una mayor probabilidad de ganancia pero con un crédito neto menor en comparación con el spread mariposa.
Vender un straddle (vender una opción de venta y una opción de compra al mismo precio de ejercicio) le daría al operador una ganancia mayor que una opción mariposa si el precio final de la acción está cerca del precio de ejercicio, pero podría resultar en una gran pérdida.
Similar al straddle es el strangle que también se construye con un call y un put, pero cuyos strikes son diferentes, reduciendo el débito neto de la operación, pero también reduciendo el riesgo de pérdida en la operación.
Una estrategia muy conocida es la llamada cubierta , en la que un operador compra una acción (o mantiene una posición en acciones previamente comprada) y vende una llamada. (Esto puede contrastarse con una llamada desnuda . Véase también venta desnuda ). Si el precio de la acción sube por encima del precio de ejercicio, la llamada se ejercerá y el operador obtendrá una ganancia fija. Si el precio de la acción baja, la llamada no se ejercerá y cualquier pérdida sufrida por el operador será parcialmente compensada por la prima recibida por la venta de la llamada. En general, los pagos coinciden con los pagos por la venta de una opción de venta. Esta relación se conoce como paridad put-call y ofrece información para la teoría financiera. Un índice de referencia para el rendimiento de una estrategia de compra-venta es el índice CBOE S&P 500 BuyWrite (símbolo de cotización BXM).
Otra estrategia muy común es la opción put protectora , en la que un operador compra una acción (o mantiene una posición larga en acciones previamente comprada) y compra una opción put. Esta estrategia actúa como un seguro cuando se invierte en largo en la acción subyacente, cubriendo las pérdidas potenciales del inversor, pero también reduciendo una ganancia que de otro modo sería mayor, si solo se compraran las acciones sin la opción put. La ganancia máxima de una opción put protectora es teóricamente ilimitada, ya que la estrategia implica tener una posición larga en la acción subyacente. La pérdida máxima se limita al precio de compra de la acción subyacente menos el precio de ejercicio de la opción put y la prima pagada. Una opción put protectora también se conoce como opción put casada.
Tipos
Las opciones se pueden clasificar de varias maneras.
Según los derechos de opción
- Las opciones de compra otorgan al tenedor el derecho (pero no la obligación) de comprar algo a un precio específico durante un período de tiempo específico.
- Las opciones de venta otorgan al tenedor el derecho (pero no la obligación) de vender algo a un precio específico durante un período de tiempo específico.
Según el tipo de entrega
- La opción de entrega física requiere que se realice la entrega real de los bienes o existencias.
- La opción liquidada en efectivo se liquida mediante el pago en efectivo resultante.
Según los activos subyacentes
- Opción sobre acciones
- Opción de bonos
- Opción futura
- Opción de índice
- Opción de materias primas
- Opción de moneda
- Opción de intercambio
Otros tipos de opciones
Otra clase importante de opciones, particularmente en los EE. UU., son las opciones sobre acciones para empleados , que una empresa otorga a sus empleados como una forma de compensación de incentivo. Existen otros tipos de opciones en muchos contratos financieros. Por ejemplo, las opciones sobre bienes raíces se utilizan a menudo para reunir grandes parcelas de tierra, y las opciones de pago anticipado suelen incluirse en los préstamos hipotecarios . Sin embargo, muchos de los principios de valoración y gestión de riesgos se aplican a todas las opciones financieras.
Estilos de opciones
Las opciones se clasifican en varios estilos, siendo los más comunes:
- Opción americana : opción que puede ejercerse cualquier día de negociación antes o antes del vencimiento .
- Opción europea : opción que solo puede ejercerse al vencimiento.
A menudo se las describe como opciones simples . Otros estilos incluyen:
- Opción bermudeña : opción que puede ejercerse únicamente en fechas específicas antes o antes del vencimiento.
- Opción asiática : una opción cuyo rendimiento está determinado por el precio subyacente promedio durante un período de tiempo predeterminado.
- Opción de barrera : cualquier opción con la característica general de que el precio del valor subyacente debe superar un determinado nivel o "barrera" antes de poder ejercerse.
- Opción binaria : una opción de todo o nada que paga el monto total si el valor subyacente cumple la condición definida al vencimiento; de lo contrario, vence.
- Opción exótica : cualquiera de una amplia categoría de opciones que pueden incluir estructuras financieras complejas. [15]
Valuación
Dado que los valores de los contratos de opciones dependen de una serie de variables diferentes además del valor del activo subyacente, su valoración es compleja. Existen muchos modelos de fijación de precios en uso, aunque todos incorporan esencialmente los conceptos de fijación racional de precios (es decir, neutralidad de riesgo ), rentabilidad , valor temporal de la opción y paridad put-call .
La valoración en sí combina un modelo del comportamiento ( "proceso" ) del precio subyacente con un método matemático que devuelve la prima como una función del comportamiento asumido. Los modelos van desde el modelo Black-Scholes (prototípico) para acciones, [16] [¿ fuente poco confiable? ] [17] hasta el marco Heath-Jarrow-Morton para tasas de interés, hasta el modelo Heston donde la volatilidad en sí se considera estocástica . Consulte Precios de activos para obtener una lista de los diversos modelos aquí.
Descomposición básica
En sus términos más básicos, el valor de una opción comúnmente se descompone en dos partes:
- La primera parte es el valor intrínseco , que se define como la diferencia entre el valor de mercado del subyacente y el precio de ejercicio de la opción dada.
- La segunda parte es el valor temporal , que depende de un conjunto de otros factores que, a través de una interrelación multivariable y no lineal, reflejan el valor esperado descontado de esa diferencia al vencimiento.
Modelos de valoración
Como se mencionó anteriormente, el valor de la opción se estima utilizando una variedad de técnicas cuantitativas, todas basadas en el principio de fijación de precios neutral al riesgo y utilizando el cálculo estocástico en su solución. El modelo más básico es el modelo Black-Scholes . Se utilizan modelos más sofisticados para modelar la sonrisa de volatilidad . Estos modelos se implementan utilizando una variedad de técnicas numéricas. [18] En general, los modelos de valoración de opciones estándar dependen de los siguientes factores:
- El precio de mercado actual del valor subyacente
- El precio de ejercicio de la opción, en particular en relación con el precio de mercado actual del activo subyacente (dentro del dinero vs. fuera del dinero)
- El costo de mantener una posición en el valor subyacente, incluidos intereses y dividendos.
- El tiempo hasta el vencimiento junto con cualquier restricción sobre cuándo puede ocurrir el ejercicio.
- una estimación de la volatilidad futura del precio del valor subyacente durante la vida de la opción
Los modelos más avanzados pueden requerir factores adicionales, como una estimación de cómo cambia la volatilidad a lo largo del tiempo y para varios niveles de precios subyacentes, o la dinámica de las tasas de interés estocásticas.
Las siguientes son algunas de las principales técnicas de valoración utilizadas en la práctica para evaluar los contratos de opciones.
Negro-Scholes
Tras los primeros trabajos de Louis Bachelier y los posteriores de Robert C. Merton , Fischer Black y Myron Scholes hicieron un gran avance al derivar una ecuación diferencial que debe ser satisfecha por el precio de cualquier derivado que dependa de una acción que no pague dividendos. Al emplear la técnica de construir una cartera neutral al riesgo que replica los retornos de la tenencia de una opción, Black y Scholes produjeron una solución de forma cerrada para el precio teórico de una opción europea. [19] Al mismo tiempo, el modelo genera parámetros de cobertura necesarios para una gestión eficaz del riesgo de las tenencias de opciones.
Si bien las ideas detrás del modelo Black-Scholes fueron innovadoras y finalmente llevaron a Scholes y Merton a recibir el Premio asociado al Logro en Economía del Banco Central Sueco (también conocido como el Premio Nobel de Economía), [20] la aplicación del modelo en el comercio de opciones real es torpe debido a los supuestos de comercio continuo, volatilidad constante y una tasa de interés constante. Sin embargo, el modelo Black-Scholes sigue siendo uno de los métodos y fundamentos más importantes para el mercado financiero existente en el que el resultado está dentro del rango razonable. [21]
Modelos de volatilidad estocástica
Desde el colapso del mercado de 1987 , se ha observado que la volatilidad implícita del mercado para opciones con precios de ejercicio más bajos es típicamente más alta que para precios de ejercicio más altos, lo que sugiere que la volatilidad varía tanto con el tiempo como con el nivel de precios del valor subyacente –la llamada sonrisa de volatilidad ; y con una dimensión temporal, una superficie de volatilidad .
El enfoque principal aquí es tratar la volatilidad como estocástica , con los modelos de volatilidad estocástica resultantes y el modelo de Heston como prototipo; [22] véase #Risk-neutral_measure para una discusión de la lógica. Otros modelos incluyen los modelos de volatilidad CEV y SABR . Sin embargo, una ventaja principal del modelo de Heston es que se puede resolver en forma cerrada, mientras que otros modelos de volatilidad estocástica requieren métodos numéricos complejos . [22]
Un enfoque alternativo, aunque relacionado, es aplicar un modelo de volatilidad local , donde la volatilidad se trata como una función determinista tanto del nivel actual de activos como del tiempo . Como tal, un modelo de volatilidad local es una generalización del modelo de Black-Scholes , donde la volatilidad es una constante. El concepto fue desarrollado cuando Bruno Dupire [23] y Emanuel Derman e Iraj Kani [24] observaron que existe un proceso de difusión único consistente con las densidades neutrales al riesgo derivadas de los precios de mercado de las opciones europeas. Véase #Desarrollo para una discusión.
Modelos de tasa corta
Para la valoración de opciones sobre bonos , swaptions (es decir, opciones sobre swaps ) y topes y pisos de tasas de interés (efectivamente, opciones sobre la tasa de interés) se han desarrollado varios modelos de tasa a corto plazo (aplicables, de hecho, a los derivados de tasa de interés en general). Los más conocidos de estos son Black-Derman-Toy y Hull–White . [25] Estos modelos describen la evolución futura de las tasas de interés al describir la evolución futura de la tasa a corto plazo. El otro marco principal para el modelado de la tasa de interés es el marco Heath–Jarrow–Morton (HJM). La distinción es que HJM da una descripción analítica de toda la curva de rendimiento , en lugar de solo la tasa a corto plazo. (El marco HJM incorpora el modelo Brace–Gatarek–Musiela y los modelos de mercado. Y algunos de los modelos de tasa a corto plazo se pueden expresar directamente en el marco HJM). Para algunos propósitos, por ejemplo, la valoración de títulos respaldados por hipotecas , esto puede ser una gran simplificación; independientemente de ello, el marco a menudo se prefiere para modelos de mayor dimensión. Téngase en cuenta que para las opciones más simples aquí, es decir, las mencionadas inicialmente, se puede emplear el modelo Black , con ciertas suposiciones.
Implementación del modelo
Una vez elegido un modelo de valoración, se utilizan diversas técnicas para implementarlo.
Técnicas analíticas
En algunos casos, se puede tomar el modelo matemático y, utilizando métodos analíticos, desarrollar soluciones en forma cerrada , como el modelo Black–Scholes y el modelo Black . Las soluciones resultantes son fácilmente computables, al igual que sus "griegas" . Aunque el modelo Roll–Geske–Whaley se aplica a una opción call americana con un dividendo, para otros casos de opciones americanas , no se encuentran disponibles soluciones en forma cerrada; las aproximaciones en este caso incluyen Barone-Adesi y Whaley , Bjerksund y Stensland y otros.
Modelo de precios de árbol binomial
Siguiendo de cerca la derivación de Black y Scholes, John Cox , Stephen Ross y Mark Rubinstein desarrollaron la versión original del modelo binomial de precios de opciones . [26] [27] Modela la dinámica del valor teórico de la opción para intervalos de tiempo discretos durante la vida de la opción. El modelo comienza con un árbol binomial de posibles precios futuros discretos de acciones subyacentes. Al construir una cartera sin riesgo de una opción y una acción (como en el modelo de Black-Scholes), se puede utilizar una fórmula simple para encontrar el precio de la opción en cada nodo del árbol. Este valor puede aproximarse al valor teórico producido por Black-Scholes, con el grado deseado de precisión. Sin embargo, el modelo binomial se considera más preciso que Black-Scholes porque es más flexible; por ejemplo, los pagos de dividendos futuros discretos se pueden modelar correctamente en los pasos de tiempo hacia adelante adecuados, y las opciones estadounidenses se pueden modelar así como las europeas. Los modelos binomiales son ampliamente utilizados por los operadores de opciones profesionales. El árbol trinomial es un modelo similar, que permite una trayectoria ascendente, descendente o estable; aunque se considera más preciso, en particular cuando se modelan menos pasos de tiempo, se utiliza con menos frecuencia porque su implementación es más compleja. Para una discusión más general, así como para la aplicación a materias primas, tasas de interés e instrumentos híbridos, consulte el modelo reticular (finanzas) .
Modelos de Montecarlo
En el caso de muchas clases de opciones, las técnicas de valoración tradicionales son inviables debido a la complejidad del instrumento. En estos casos, un enfoque de Monte Carlo puede resultar útil. En lugar de intentar resolver las ecuaciones diferenciales de movimiento que describen el valor de la opción en relación con el precio del título subyacente, un modelo de Monte Carlo utiliza la simulación para generar trayectorias de precios aleatorias del activo subyacente, cada una de las cuales da como resultado un pago por la opción. El promedio de estos pagos se puede descontar para obtener un valor esperado para la opción. [28] Sin embargo, cabe señalar que, a pesar de su flexibilidad, el uso de la simulación para las opciones de estilo americano es algo más complejo que para los modelos basados en celosía.
Modelos de diferencias finitas
Las ecuaciones utilizadas para modelar la opción se expresan a menudo como ecuaciones diferenciales parciales (véase, por ejemplo, la ecuación de Black-Scholes ). Una vez expresada en esta forma, se puede derivar un modelo de diferencias finitas y obtener la valoración. Existe una serie de implementaciones de métodos de diferencias finitas para la valoración de opciones, entre ellas: la diferencia finita explícita , la diferencia finita implícita y el método de Crank-Nicolson . Se puede demostrar que un modelo de fijación de precios de opciones de árbol trinomial es una aplicación simplificada del método de diferencia finita explícita. Aunque el enfoque de la diferencia finita es matemáticamente sofisticado, es particularmente útil cuando se suponen cambios a lo largo del tiempo en los datos de entrada del modelo (por ejemplo, el rendimiento de los dividendos, la tasa libre de riesgo o la volatilidad, o alguna combinación de estos) que no son manejables en forma cerrada.
Otros modelos
Otras implementaciones numéricas que se han utilizado para valorar opciones incluyen métodos de elementos finitos .
Riesgos
| Ejemplo: Una opción de compra (también conocida como CO) que vence en 99 días sobre 100 acciones de XYZ tiene un precio de ejercicio de $50, y XYZ cotiza actualmente a $48. Con una volatilidad futura realizada durante la vida de la opción estimada en un 25%, el valor teórico de la opción es $1,89. Los parámetros de cobertura , , , son (0,439, 0,0631, 9,6 y −0,022), respectivamente. Supongamos que al día siguiente, la acción de XYZ sube a $48,5 y la volatilidad cae al 23,5%. Podemos calcular el valor estimado de la opción de compra aplicando los parámetros de cobertura a las nuevas entradas del modelo como: En este escenario, el valor de la opción aumenta en $0,0614 hasta $1,9514, lo que genera una ganancia de $6,14. Tenga en cuenta que, en el caso de una cartera con delta neutral, en la que el operador también hubiera vendido 44 acciones de XYZ como cobertura, la pérdida neta en el mismo escenario sería de ($15,86). |
Al igual que con todos los valores, la negociación de opciones conlleva el riesgo de que el valor de la opción cambie con el tiempo. Sin embargo, a diferencia de los valores tradicionales, el rendimiento de la tenencia de una opción varía de forma no lineal con el valor del activo subyacente y otros factores. Por lo tanto, los riesgos asociados con la tenencia de opciones son más complicados de comprender y predecir.
Parámetros de cobertura estándar
En general, el cambio en el valor de una opción se puede derivar del lema de Itô como:
donde los griegos , , y son los parámetros de cobertura estándar calculados a partir de un modelo de valoración de opciones, como Black–Scholes , y , y son cambios unitarios en el precio del subyacente, la volatilidad del subyacente y el tiempo, respectivamente.
De este modo, en cualquier momento, se puede estimar el riesgo inherente a la tenencia de una opción calculando sus parámetros de cobertura y luego estimando el cambio esperado en los valores de entrada del modelo, , y , siempre que los cambios en estos valores sean pequeños. Esta técnica se puede utilizar de manera eficaz para comprender y gestionar los riesgos asociados a las opciones estándar. Por ejemplo, al compensar la tenencia de una opción con la cantidad de acciones del subyacente, un operador puede formar una cartera delta neutral que esté cubierta contra pérdidas por pequeños cambios en el precio del subyacente. La fórmula de sensibilidad al precio correspondiente para esta cartera es:
Riesgo de pin
Una situación especial llamada riesgo de pin puede surgir cuando el activo subyacente cierra en el valor de ejercicio de la opción o muy cerca de él el último día en que se negocia la opción antes del vencimiento. El emisor de la opción (vendedor) puede no saber con certeza si la opción será efectivamente ejercida o si se le permitirá vencer. Por lo tanto, el emisor de la opción puede terminar con una posición residual grande e indeseada en el activo subyacente cuando los mercados abran el siguiente día de negociación después del vencimiento, independientemente de sus mejores esfuerzos para evitar dicho residual.
Riesgo de contraparte
Otro riesgo, que a menudo se pasa por alto, en los derivados como las opciones es el riesgo de contraparte . En un contrato de opciones, este riesgo es que el vendedor no venda o compre el activo subyacente según lo acordado. El riesgo se puede minimizar utilizando un intermediario financieramente sólido capaz de hacer frente a la operación, pero en caso de pánico o desplome importante, el número de incumplimientos puede abrumar incluso a los intermediarios más fuertes.
Niveles de aprobación de opciones
Para limitar el riesgo, los corredores utilizan sistemas de control de acceso para restringir que los operadores ejecuten ciertas estrategias de opciones que no serían adecuadas para ellos. Los corredores generalmente ofrecen alrededor de cuatro o cinco niveles de aprobación, siendo el nivel más bajo el que ofrece el menor riesgo y el nivel más alto el que ofrece el mayor riesgo. La cantidad real de niveles y las estrategias de opciones específicas permitidas en cada nivel varían entre corredores. Los corredores también pueden tener sus propios criterios de investigación específicos, pero generalmente se basan en factores como el salario anual y el patrimonio neto del operador, la experiencia comercial y los objetivos de inversión (preservación de capital, ingresos, crecimiento o especulación). Por ejemplo, un operador con un salario y patrimonio neto bajos, poca experiencia comercial y solo preocupado por preservar el capital generalmente no estaría autorizado a ejecutar estrategias de alto riesgo como opciones de compra y venta al descubierto . Los operadores pueden actualizar su información cuando solicitan permiso para actualizar a un nivel de aprobación más alto. [29]
Intercambios de opciones
Bolsa de Opciones de Chicago (CBOE)
La Bolsa de Opciones de Chicago (CBOE) es una bolsa de opciones ubicada en Chicago, Illinois. Fundada en 1973, la CBOE es la primera bolsa de opciones en los Estados Unidos. La CBOE ofrece operaciones con opciones sobre diversos valores subyacentes, incluidos índices de mercado, fondos cotizados en bolsa (ETF), acciones e índices de volatilidad. Su producto estrella son las opciones sobre el índice S&P 500 (SPX), una de las opciones más negociadas a nivel mundial. Además de su negociación a viva voz en el piso, la CBOE también opera una plataforma de negociación completamente electrónica . La CBOE está regulada por la Comisión de Bolsa y Valores de los Estados Unidos (SEC). [30]
Nasdaq OMX PHLX
Fundada en 1790, la Bolsa de Valores de Filadelfia (NASDAQ OMX PHLX) , también conocida como la Bolsa de Valores de Filadelfia , es una bolsa de opciones y futuros ubicada en Filadelfia, Pensilvania. Es la bolsa de valores más antigua de los Estados Unidos. La NASDAQ OMX PHLX permite la negociación de opciones sobre acciones, índices, ETF y divisas extranjeras. Es una de las pocas bolsas designadas para la negociación de opciones sobre divisas en los EE. UU. En 2008, NASDAQ adquirió la Bolsa de Valores de Filadelfia y la rebautizó como NASDAQ OMX PHLX. Opera como una subsidiaria de NASDAQ, Inc. [31]
Bolsa Internacional de Valores (ISE)
La Bolsa Internacional de Valores (ISE) es una bolsa de opciones electrónica ubicada en la ciudad de Nueva York. Fundada en 2000, ISE fue la primera bolsa de opciones totalmente electrónica de Estados Unidos. ISE ofrece la posibilidad de negociar opciones sobre acciones, índices y ETF estadounidenses. Su plataforma de negociación ofrece una subasta de mejora de precio máximo para permitir que los creadores de mercado compitan por las órdenes. ISE está regulada por la SEC y es propiedad de Nasdaq, Inc. [32]
Bolsa de valores Eurex
Eurex Exchange es una bolsa de derivados ubicada en Frankfurt, Alemania. Ofrece operaciones con futuros y opciones sobre tipos de interés, acciones, índices y productos de renta fija. Formada en 1998 a partir de la fusión de Deutsche Terminbörse (DTB) y Swiss Options and Financial Futures Exchange (SOFFEX), Eurex Exchange opera plataformas de operaciones electrónicas y a viva voz. Eurex Exchange es propiedad de Eurex Frankfurt AG. [33]
Bolsa de Tokio (TSE)
Fundada en 1878, la Bolsa de Valores de Tokio (TSE) es una bolsa de valores ubicada en Tokio, Japón. Además de acciones, la TSE también ofrece operaciones con futuros y opciones sobre índices bursátiles. Las operaciones se realizan de forma electrónica y a través de subastas de empresas de valores. La TSE está regulada por la Agencia de Servicios Financieros de Japón. Es propiedad del Japan Exchange Group . [34]
Véase también
- Bolsa de Valores de Estados Unidos
- Contrato de opciones de rendimiento por área
- Ascot (finanzas)
- Bolsa de Opciones de Chicago Board
- Seguridad dilutiva
- Euroex
- Euronext.liffe
- Bolsa de valores internacional
- Bolsa de Valores de Nueva York
- Bolsa de Valores de Filadelfia
- LEAPS (finanzas)
- Opciones retroactivas
- Corporación de compensación de opciones
- Spread de opciones
- Estrategia de opciones
- Símbolo de opción
- Análisis de opciones reales
- Explicación de PnL
- Riesgo de pin (opciones)
- XVA
Referencias
- ^ Abraham, Stephan (13 de mayo de 2010). «Historia de las opciones financieras - Investopedia». Investopedia . Consultado el 2 de junio de 2014 .
- ^ Mattías Sander. Representación de Bondesson del modelo de varianza gamma y fijación de precios de opciones de Monte Carlo. Lunds Tekniska Högskola 2008
- ^ Aristóteles. Política.
- ^ Josef de la Vega. Confusión de confusiones . 1688. Fragmentos descriptivos de la Bolsa de Amsterdam seleccionados y traducidos por el profesor Hermann Kellenbenz. Biblioteca Baker, Escuela de Posgrado en Administración de Empresas de Harvard, Boston, Massachusetts.
- ^ Smith, B. Mark (2003), Historia del mercado de valores mundial desde la antigua Roma hasta Silicon Valley , University of Chicago Press, pág. 20, ISBN 0-226-76404-4
- ^ Brealey, Richard A .; Myers, Stewart (2003), Principios de finanzas corporativas (7.ª ed.), McGraw-Hill, Capítulo 20
- ^ Hull, John C. (2005), Opciones, futuros y otros derivados (extracto de Fan Zhang) (6.ª ed.), Prentice-Hall, pág. 6, ISBN 0-13-149908-4, archivado desde el original el 29 de julio de 2016 , consultado el 21 de abril de 2008
- ^ Características y riesgos de las opciones estandarizadas, Options Clearing Corporation , consultado el 15 de julio de 2020
- ^ Comercio de productos CME, Chicago Mercantile Exchange , consultado el 21 de junio de 2007
- ^ ISE Traded Products, International Securities Exchange, archivado desde el original el 11 de mayo de 2007 , consultado el 21 de junio de 2007
- ^ Elinor Mills (12 de diciembre de 2006), Google presenta una subasta de opciones sobre acciones poco ortodoxa, CNet , consultado el 19 de junio de 2007
- ^ Harris, Larry (2003), Comercio e intercambios , Oxford University Press, págs. 26-27
- ^ Invest-FAQ o Ley y valoración para el tamaño típico del contrato de opción
- ^ "Entender las opciones sobre acciones" (PDF) . The Options Clearing Corporation y CBOE . Consultado el 27 de agosto de 2015 .
- ^ Fabozzi, Frank J. (2002). Manual de instrumentos financieros (1.ª ed.). Nueva Jersey : John Wiley and Sons. pág. 471. ISBN 0-471-22092-2.
- ^ Benhamou, Eric. "Opciones antes de Black Scholes" (PDF) . Eric Benhamou .
- ^ Black, Fischer; Scholes, Myron (1973). "La fijación de precios de opciones y pasivos corporativos". Revista de Economía Política . 81 (3): 637–654. doi :10.1086/260062. JSTOR 1831029. S2CID 154552078.
- ^ Reilly, Frank K.; Brown, Keith C. (2003). Análisis de inversiones y gestión de carteras (7.ª ed.). Thomson Southwestern. Capítulo 23.
- ^ Black, Fischer y Myron S. Scholes. "La fijación de precios de opciones y pasivos corporativos", Journal of Political Economy, 81 (3), 637–654 (1973).
- ^ Das, Satyajit (2006), Traders, Guns & Money: Knowns and unknowns in the dezzling world of deriveds (6.ª ed.), Londres: Prentice-Hall, Capítulo 1 'Arma de destrucción masiva financiera: demagogia de los derivados', pág. 22, ISBN 978-0-273-70474-4
- ^ Hull, John C. (2005), Opciones, futuros y otros derivados (6.ª ed.), Prentice-Hall, ISBN 0-13-149908-4
- ^ por Jim Gatheral (2006), La superficie de volatilidad, una guía para profesionales , Wiley Finance, ISBN 978-0-471-79251-2
- ^ Bruno Dupire (julio de 2007) [enero de 1994]. «Fijar precios con una sonrisa» (PDF) . Riesgo . Archivado desde el original (PDF) el 7 de septiembre de 2012. Consultado el 14 de junio de 2013 .
- ^ Derman, E.; Iraj Kani (enero de 1994). "Riding on a Smile" (PDF) . Notas de investigación sobre estrategias cuantitativas . Goldman Sachs. Archivado desde el original (PDF) el 10 de julio de 2011. Consultado el 1 de junio de 2007 .
- ^ Análisis de renta fija , pág. 410, en Google Books
- ^ Cox, JC , Ross SA y Rubinstein M. 1979. Fijación de precios de opciones: un enfoque simplificado, Journal of Financial Economics , 7:229–263.[1]
- ^ Cox, John C .; Rubinstein, Mark (1985), Mercados de opciones , Prentice-Hall, Capítulo 5
- ^ Crack, Timothy Falcon (2004), Black-Scholes básico: fijación de precios y negociación de opciones, Timothy Crack, págs. 91-102, ISBN 0-9700552-2-6
- ^ "Boletín del inversor: Apertura de una cuenta de opciones". Comisión de Bolsa y Valores de Estados Unidos . 18 de marzo de 2015. Consultado el 27 de agosto de 2022 .
- ^ Baker, Howard (2023). "50 años de opciones negociadas en bolsa. Cboe celebra su aniversario de oro" (PDF) . moaf.org . págs. 20–23.
- ^ "Nasdaq: índice Nasdaq (PHLX)".
- ^ "Bolsa Internacional de Valores Nasdaq (ISE)".
- ^ "Sobre nosotros". www.eurex.com . Consultado el 3 de marzo de 2024 .
- ^ "Japan Exchange Group". Japan Exchange Group . Consultado el 3 de marzo de 2024 .
Lectura adicional
- Fischer Black y Myron S. Scholes. "La fijación de precios de opciones y pasivos corporativos", Journal of Political Economy , 81 (3), 637–654 (1973).
- Feldman, Barry y Dhuv Roy. "Estrategias de inversión pasivas basadas en opciones: el caso del índice CBOE S&P 500 BuyWrite". The Journal of Investing (verano de 2005).
- Kleinert, Hagen , Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets , 4.ª edición, World Scientific (Singapur, 2004); ISBN 981-238-107-4 (también disponible en línea: archivos PDF)
- Hill, Joanne, Venkatesh Balasubramanian, Krag (Buzz) Gregory e Ingrid Tierens. "Finding Alpha via Covered Index Writing" (Cómo encontrar alfa mediante la redacción de índices cubiertos). Financial Analysts Journal (septiembre-octubre de 2006). págs. 29-46.
- Millman, Gregory J. (2008), "Mercados de futuros y opciones", en David R. Henderson (ed.), Concise Encyclopedia of Economics (2.ª ed.), Indianápolis: Biblioteca de Economía y Libertad , ISBN 978-0-86597-665-8, OCLC 237794267
- Natenberg, Sheldon (2015). Volatilidad y fijación de precios de opciones: estrategias y técnicas de negociación avanzadas (segunda edición). Nueva York. ISBN 978-0-07-181877-3.
{{cite book}}: CS1 maint: location missing publisher (link) - Moran, Matthew. "Rendimiento ajustado al riesgo para índices basados en derivados: herramientas para ayudar a estabilizar los rendimientos". The Journal of Indexes (Cuarto trimestre de 2002), págs. 34-40.
- Reilly, Frank y Keith C. Brown, Análisis de inversiones y gestión de carteras, 7.ª edición, Thompson Southwestern, 2003, págs. 994–5.
- Schneeweis, Thomas y Richard Spurgin. "Los beneficios de las estrategias basadas en opciones sobre índices para carteras institucionales" , The Journal of Alternative Investments (primavera de 2001), págs. 44-52.
- Whaley, Robert. "Riesgo y rentabilidad del índice mensual CBOE BuyWrite" , The Journal of Derivatives (invierno de 2002), págs. 35-42.
- Bloss, Michael; Ernst, Dietmar; Häcker Joachim (2008): Derivados: una guía autorizada sobre derivados para intermediarios financieros e inversores Oldenbourg Verlag München ISBN 978-3-486-58632-9
- Espen Gaarder Haug y Nassim Nicholas Taleb (2008): "Por qué nunca hemos utilizado la fórmula de fijación de precios de opciones Black-Scholes-Merton"














