Plaza de la oposición
Este artículo necesita citas adicionales para su verificación . ( febrero de 2015 ) |


En lógica de términos (una rama de la lógica filosófica ), el cuadrado de oposición es un diagrama que representa las relaciones entre las cuatro proposiciones categóricas básicas . El origen del cuadrado se remonta al tratado de Aristóteles Sobre la interpretación y su distinción entre dos oposiciones: contradicción y contrariedad . Sin embargo, Aristóteles no dibujó ningún diagrama; esto lo hicieron varios siglos después Apuleyo y Boecio .
Resumen
En la lógica tradicional , una proposición (latín: propositio ) es una afirmación hablada ( oratio enunciativa ), no el significado de una afirmación, como en la filosofía del lenguaje y la lógica modernas . Una proposición categórica es una proposición simple que contiene dos términos, sujeto ( S ) y predicado ( P ), en la que el predicado se afirma o se niega del sujeto.
Toda proposición categórica puede reducirse a una de cuatro formas lógicas , llamadas A , E , I y O, basadas en el latín a ff i rmo (yo afirmo), para las proposiciones afirmativas A e I , y n e g o (yo niego), para las proposiciones negativas E y O. Estas son:
- La proposición A , la afirmativa universal ( universalis assertiva ), cuya forma en latín es 'omne S est P ', traducida habitualmente como 'todo S es un P '.
- La proposición E , la negativa universal ( universalis negativa ), forma latina 'nullum S est P ', normalmente traducida como 'no hay S son P '.
- La proposición I , la afirmativa particular ( particularis afirmativa ), latina 'quoddam S est P ', normalmente traducida como 'algunas S son P '.
- La proposición O , la negativa particular ( particularis negativa ), latina 'quoddam S nōn est P ', normalmente traducida como 'algunas S no son P '.
En forma de tabla:
| Nombre | Símbolo | latín | Inglés* | Mnemotécnico | Forma moderna [1] |
|---|---|---|---|---|---|
| Afirmativo universal | A | Todo está en P. | Todo S es P. ( S siempre es P. ) | afirmo ( yo afirmo) | |
| Negativo universal | mi | Nulo S est P. | No S es P. ( S nunca es P. ) | n e go (lo niego) | |
| Afirmativo particular | I | ¿Qué es S est P ? | Algunos S son P. ( S es a veces P. ) | aff i rmo (yo afirmo) | |
| Particularmente negativo | Oh | Quoddam S no es P. | Alguna S no es P. ( S no siempre es P. ) | neg o (niego) |
* La proposición A puede enunciarse como "Todo S es P ". Sin embargo, la proposición E , cuando se enuncia como "Todo S no es P ", es ambigua [2] porque puede ser una proposición E o una proposición O , por lo que requiere un contexto para determinar la forma; la forma estándar "Ningún S es P " es inequívoca, por lo que se prefiere. La proposición O también adopta las formas "A veces S no es P " y "Un cierto S no es P " (literalmente, el latín 'Quoddam S nōn est P ').
** en las formas modernas significa que una declaración se aplica a un objeto . Puede interpretarse simplemente como " es " en muchos casos. También puede escribirse como .
Aristóteles afirma (en los capítulos seis y siete del Peri hermēneias (Περὶ Ἑρμηνείας, latín De Interpretatione , español 'Sobre la interpretación')) que existen ciertas relaciones lógicas entre estos cuatro tipos de proposiciones. Dice que a cada afirmación corresponde exactamente una negación, y que cada afirmación y su negación son 'opuestas' de tal manera que siempre una de ellas debe ser verdadera y la otra falsa. Un par de una afirmación y su negación es, él llama, una ' contradicción ' (en latín medieval, contradictio ). Ejemplos de contradicciones son 'todo hombre es blanco' y 'no todo hombre es blanco' (también leído como 'algunos hombres no son blancos'), 'ningún hombre es blanco' y 'algún hombre es blanco'.
Las relaciones que se indican a continuación, contraria, subcontraria, subalternancia y superalternación, se cumplen si se parte del supuesto lógico tradicional de que existen cosas enunciadas como S (o cosas que satisfacen una afirmación S en la lógica moderna). Si se elimina este supuesto, estas relaciones no se cumplen.
Los enunciados " contrarios " (medieval: contrariae ) son aquellos en los que ambos enunciados no pueden ser verdaderos al mismo tiempo. Ejemplos de estos son la afirmación universal "todo hombre es blanco" y la negativa universal "ningún hombre es blanco". Estas no pueden ser verdaderas al mismo tiempo. Sin embargo, no son contradictorias porque ambas pueden ser falsas. Por ejemplo, es falso que todo hombre sea blanco, ya que algunos hombres no son blancos. Sin embargo, también es falso que ningún hombre sea blanco, ya que hay algunos hombres blancos.
Puesto que cada enunciado tiene su opuesto contradictorio (su negación), y puesto que un enunciado contradictorio es verdadero cuando su opuesto es falso, se sigue que los opuestos de los contrarios (que los medievales llamaban subcontrarios , subcontrariae ) pueden ser ambos verdaderos, pero no pueden ser ambos falsos. Puesto que los subcontrarios son negaciones de enunciados universales, los lógicos medievales los llamaban enunciados «particulares».
Otra relación lógica implicada por esto, aunque no mencionada explícitamente por Aristóteles, es la "alternancia" ( alternatio ), que consiste en " subalternidad " y " superalternidad ". La subalternidad es una relación entre el enunciado particular y el enunciado universal de la misma calidad (afirmativo o negativo) tal que el particular está implicado por el universal, mientras que la superalternación es una relación entre ellos tal que la falsedad del universal (equivalentemente la negación del universal) está implicada por la falsedad del particular (equivalentemente la negación del particular). [3] (La superalternación es la contrapositiva de la subalternidad.) En estas relaciones, el particular es el subalterno del universal, que es el superalterno del particular. Por ejemplo, si "todo hombre es blanco" es verdadero, su contrario "ningún hombre es blanco" es falso. Por lo tanto, el contradictorio "algún hombre es blanco" es verdadero. De manera similar, el universal “ningún hombre es blanco” implica el particular “no todo hombre es blanco”. [4] [5]
En resumen:
- Los enunciados universales son contrarios: «todo hombre es justo» y «ningún hombre es justo» no pueden ser verdaderos juntos, aunque uno puede ser verdadero y el otro falso, y también ambos pueden ser falsos (si al menos un hombre es justo y al menos un hombre no es justo).
- Las afirmaciones particulares son subcontrarias. “Algún hombre es justo” y “algún hombre no es justo” no pueden ser falsas juntas.
- El enunciado particular de una cualidad es el subalterno del enunciado universal de esa misma cualidad, que es el superalterno del enunciado particular porque en la semántica aristotélica 'cada A es B ' implica 'algún A es B ' y 'ningún A es B ' implica 'algún A no es B '. Nótese que las interpretaciones formales modernas de oraciones en inglés interpretan 'cada A es B ' como 'para cualquier x , un enunciado de que x es A implica un enunciado de que x es B ', lo que no implica 'algún x es A' . Sin embargo, esto es una cuestión de interpretación semántica y no significa, como a veces se afirma, que la lógica aristotélica esté 'equivocada'.
- La afirmativa universal ( A ) y la negativa particular ( O ) son contradictorias. Si algún A no es B , entonces no todo A es B. A la inversa, aunque este no es el caso en la semántica moderna, se pensaba que si todo A no es B , algún A no es B. Esta interpretación ha causado dificultades (ver más abajo). Mientras que el griego de Aristóteles no representa la negativa particular como 'algún A no es B' , sino como 'no todo A es B ', alguien en su comentario sobre el Peri hermaneias , traduce la negativa particular como 'quoddam A nōn est B ', literalmente 'un cierto A no es un B ', y en todos los escritos medievales sobre lógica es habitual representar la proposición particular de esta manera.
Estas relaciones se convirtieron en la base de un diagrama que se originó con Boecio y que los lógicos medievales utilizaron para clasificar las relaciones lógicas. Las proposiciones se colocan en las cuatro esquinas de un cuadrado y las relaciones se representan como líneas dibujadas entre ellas, de ahí el nombre de "El cuadrado de la oposición". Por lo tanto, se pueden dar los siguientes casos: [6]
- Si A es verdadero, entonces E es falso, I es verdadero, O es falso;
- Si E es verdadero, entonces A es falso, I es falso, O es verdadero;
- Si I es verdadero, entonces E es falso, A y O son indeterminados;
- Si O es verdadero, entonces A es falso, E e I son indeterminados;
- Si A es falso, entonces O es verdadero, E e I son indeterminados;
- Si E es falso, entonces I es verdadero, A y O son indeterminados;
- Si I es falso, entonces A es falso, E es verdadero, O es verdadero;
- Si O es falso, entonces A es verdadero, E es falso, I es verdadero.
Para memorizarlos, los medievales inventaron la siguiente rima latina: [7]
- A adfirmat, negat E , sed universaliter ambae;
I firmat, negat O , sed particulariter ambae.
Afirma que A y E no son ni ambas verdaderas ni ambas falsas en cada uno de los casos anteriores. Lo mismo se aplica a I y O. Mientras que las dos primeras son afirmaciones universales, la pareja I / O se refiere a afirmaciones particulares.
El cuadrado de oposiciones se utilizó para las inferencias categóricas descritas por el filósofo griego Aristóteles: conversión , obversión y contraposición . Cada uno de esos tres tipos de inferencia categórica se aplicó a las cuatro formas lógicas boecianas: A , E , I y O.
El problema de la importancia existencial
Los subcontrarios ( I y O ), que los lógicos medievales representaban en la forma 'quoddam A est B ' (algún A particular es B ) y 'quoddam A non est B ' (algún A particular no es B ) no pueden ser ambos falsos, ya que sus enunciados contradictorios universales (ningún A es B / todo A es B ) no pueden ser ambos verdaderos. Esto conduce a una dificultad identificada por primera vez por Peter Abelard (1079 - 21 de abril de 1142). 'Algún A es B ' parece implicar 'algo es A ', en otras palabras, existe algo que es A. Por ejemplo, 'Algún hombre es blanco' parece implicar que al menos una cosa que existe es un hombre, a saber, el hombre que tiene que ser blanco, si 'algún hombre es blanco' es verdadero. Pero, 'algún hombre no es blanco' también implica que existe algo como hombre, a saber, el hombre que no es blanco, si el enunciado 'algún hombre no es blanco' es verdadero. Pero la lógica aristotélica exige que, necesariamente, una de estas afirmaciones (más generalmente, «un determinado A es B » y «un determinado A no es B ») sea verdadera, es decir, no pueden ser ambas falsas. Por lo tanto, puesto que ambas afirmaciones implican la presencia de al menos una cosa que es un hombre, se sigue la presencia de un hombre o de hombres. Pero, como señala Abelardo en la Dialéctica , ¿no podría ser que los hombres no existieran? [8]
- Pues si no existe absolutamente ningún hombre, ni la proposición «todo hombre es hombre» es verdadera ni la proposición «algún hombre no es hombre». [9]
Abelardo también señala que los subcontrarios que contienen términos sujetos que no denotan nada, como 'un hombre que es una piedra', son ambos falsos.
- Si es verdad que «todo hombre de piedra es una piedra», también es verdad su conversión por accidente («algunas piedras son hombres de piedra»). Pero ninguna piedra es un hombre de piedra, porque ni este hombre ni aquel hombre, etc., es una piedra. Pero también este «cierto hombre de piedra no es una piedra» es necesariamente falso, puesto que es imposible suponer que sea verdadero. [10]
Terence Parsons (nacido en 1939) sostiene que los filósofos antiguos no experimentaron el problema de la importancia existencial , ya que sólo las formas A (afirmativa universal) e I (afirmativa particular) tenían importancia existencial. (Si una afirmación incluye un término tal que la afirmación es falsa si el término no tiene instancias, es decir, no existe nada asociado con el término, entonces se dice que la afirmación tiene importancia existencial con respecto a ese término).
- Las afirmaciones tienen un significado existencial, mientras que las negativas no. Por lo tanto, los antiguos no veían la incoherencia del cuadrado tal como lo formuló Aristóteles porque no había ninguna incoherencia que ver. [11]
Continúa citando a un filósofo medieval, Guillermo de Moerbeke (1215-1235 – c. 1286 ),
- En las proposiciones afirmativas siempre se afirma que un término supone algo. Por lo tanto, si no supone nada, la proposición es falsa. Sin embargo, en las proposiciones negativas se afirma que el término no supone nada o que supone algo cuyo predicado se niega verdaderamente. Por lo tanto, una proposición negativa tiene dos causas de verdad. [12]
Y señala la traducción que Boecio hace de la obra de Aristóteles como la que da lugar a la noción errónea de que la forma O tiene importancia existencial.
- Pero cuando Boecio (477-524 d. C.) comenta este texto, ilustra la doctrina de Aristóteles con el hoy famoso diagrama y utiliza la expresión «Algunos hombres no son justos». Por lo tanto, esto debe haberle parecido un equivalente natural en latín. A nosotros nos parece extraño en inglés, pero a él no le molestaba. [13]
Cuadrados modernos de oposición
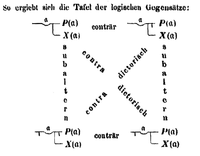
El conträr que aparece a continuación es una fe de erratas:
debería leerse subconträr .
En el siglo XIX, George Boole (noviembre de 1815 - 8 de diciembre de 1864) defendió la exigencia de un significado existencial en ambos términos de las afirmaciones particulares ( I y O ), pero permitiendo que todos los términos de las afirmaciones universales ( A y E ) carecieran de significado existencial. Esta decisión hizo que los diagramas de Venn fueran particularmente fáciles de usar para la lógica de términos. El cuadrado de oposición, bajo este conjunto booleano de supuestos, a menudo se denomina el cuadrado de oposición moderno . En el cuadrado de oposición moderno, las afirmaciones A y O son contradictorias, al igual que E e I , pero todas las demás formas de oposición dejan de ser válidas; no hay contrarios, subcontrarios, subalternancias y superalternaciones. Por lo tanto, desde un punto de vista moderno, a menudo tiene sentido hablar de "la" oposición de una afirmación, en lugar de insistir, como lo hacían los lógicos más antiguos, en que una afirmación tiene varios opuestos diferentes, que están en diferentes tipos de oposición con la afirmación.
La Begriffsschrift de Gottlob Frege (8 de noviembre de 1848 – 26 de julio de 1925) también presenta un cuadrado de oposiciones, organizado de manera casi idéntica al cuadrado clásico, mostrando las contradicciones, subalternas y contrarios entre cuatro fórmulas construidas a partir de la cuantificación universal, la negación y la implicación.
El cuadrado semiótico de Algirdas Julien Greimas (9 de marzo de 1917 - 27 de febrero de 1992) se deriva de la obra de Aristóteles.
El cuadrado tradicional de oposición se compara hoy a menudo con cuadrados basados en la negación interna y externa. [14]
Hexágonos lógicos y otros bisímplex
El cuadrado de oposición se ha extendido a un hexágono lógico que incluye las relaciones de seis enunciados. Fue descubierto independientemente por Augustin Sesmat (7 de abril de 1885 – 12 de diciembre de 1957) y Robert Blanché (1898–1975). [15] Se ha demostrado que tanto el cuadrado como el hexágono, seguidos por un " cubo lógico ", pertenecen a una serie regular de objetos n-dimensionales llamados "bi-símplex lógicos de dimensión n ". El patrón también va más allá de esto. [16]
Cuadrado de oposición (o cuadrado lógico) y lógica modal
El cuadrado lógico, también llamado cuadrado de oposición o cuadrado de Apuleyo , tiene su origen en las cuatro frases marcadas para emplear en el razonamiento silogístico: “Todo hombre es malo”, la afirmativa universal - La negación de la afirmativa universal “No todo hombre es malo” (o “Algunos hombres no son malos”) - “Algunos hombres son malos”, la afirmativa particular - y finalmente, la negación de la afirmativa particular “Ningún hombre es malo”. Robert Blanché publicó con Vrin sus Structures intellectuelles en 1966 y desde entonces muchos estudiosos piensan que el cuadrado lógico o cuadrado de oposición que representa cuatro valores debe ser reemplazado por el hexágono lógico que al representar seis valores es una figura más potente porque tiene el poder de explicar más cosas sobre la lógica y el lenguaje natural.
Interpretación de enunciados categóricos desde la perspectiva de la teoría de conjuntos
En la lógica matemática moderna , las afirmaciones que contienen las palabras "todos", "algunos" y "ninguno" se pueden formular en términos de la teoría de conjuntos si asumimos un dominio de discurso similar a un conjunto. Si el conjunto de todos los A se etiqueta como y el conjunto de todos los B como , entonces:
- "Todo A es B " (AaB) es equivalente a " es un subconjunto de ", o .
- "No A es B " (AeB) es equivalente a "La intersección de y está vacía ", o .
- "Algún A es B " (AiB) es equivalente a "La intersección de y no está vacía", o .
- "Algún A no es B " (AoB) es equivalente a " no es un subconjunto de ", o .
Por definición, el conjunto vacío es un subconjunto de todos los conjuntos. De este hecho se deduce que, según esta convención matemática, si no hay ningún A , entonces las afirmaciones «Todo A es B » y «Ningún A es B » son siempre verdaderas, mientras que las afirmaciones «Algún A es B » y «Algún A no es B » son siempre falsas. Esto también implica que AaB no implica AiB, y algunos de los silogismos mencionados anteriormente no son válidos cuando no hay ningún A ( ).
Véase también
- Silogística de Boole
- Lógica libre
- Cubo lógico
- Hexágono lógico
- Octágono de Profecías
- Triángulo de oposición
Referencias
- ^ Según El cuadrado tradicional de oposición: 1.1 La revisión moderna del cuadrado en la Enciclopedia de filosofía de Stanford
- ^ Kelley, David (2014). El arte del razonamiento: Introducción a la lógica y al pensamiento crítico (4.ª ed.). Nueva York, NY: WW Norton & Company, Inc., pág. 150. ISBN 978-0-393-93078-8.
- ^ "Introducción a la lógica - 7.2.1 Terminación del cuadrado e inferencias inmediatas". 2021-08-10.
- ^ Parry y Hacker, Lógica aristotélica (SUNY Press, 1990), pág. 158.
- ^ Cohen y Nagel, Introducción a la lógica, segunda edición (Hackett Publishing, 1993), pág. 55.
- ^ Reale, Giovanni ; Antiseri, Darío (1983). Il pensiero occidentale dalle origini a oggi . vol. 1. Brescia: Editrice La Scuola. pag. 356.ISBN 88-350-7271-9. OCLC 971192154.
- ^ Massaro, Domenico (2005). Questioni di verità: logica di base per capire e farsi capire. Guión (en italiano). vol. 2. Arces: Liguori Editore Srl. pag. 58.ISBN 9788820738921. OCLC 263451944 .
- ^ En su Dialéctica y en su comentario a las Perihermaneias
- ^ Re enim hominis prorsus non existente neque ea vera est quae ait: omnis homo est homo, nec ea quae proponit: quidam homo non est homo
- ^ Si enim vera est: Omnis homo qui lapis est, est lapis, et eius conversa per accidens vera est: Quidam lapis est homo qui est lapis. Sed nullus lapis est homo qui est lapis, quia neque hic neque ille etc. Sed et illam: Quidam homo qui est lapis, non est lapis, falsam esse necesse est, cum impossibile ponat
- ^ en El cuadrado tradicional de la oposición en la Enciclopedia de Filosofía de Stanford
- ^ (SL I.72) Loux 1974, 206
- ^ La Plaza Tradicional de la Oposición
- ^ Westerståhl, 'Cuadrados de oposición clásicos vs. modernos, y más allá', en Beziau y Payette (eds.), El cuadrado de oposición: un marco general para la cognición, Peter Lang, Berna, 195-229.
- ^ Teoría de la N-Oposición Hexágono lógico
- ^ Moretti, Pellissier
Enlaces externos
- Parsons, Terence. "El cuadrado tradicional de la oposición". En Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy .
- Congreso Internacional en la Plaza de la Oposición
- Número especial de Logica Universalis Vol. 2 N. 1 (2008) sobre el cuadrado de la oposición
- Catlogic: un script informático de código abierto escrito en Ruby para construir, investigar y calcular proposiciones categóricas y silogismos.
- Periermenias Aristotelis con enlaces a vídeo y manuscrito digitalizado LJS 101 de la traducción latina de Boecio del De representatione de Aristóteles , que contiene copias de los siglos IX/XI (algunas en color) del cuadrado de oposición de Aristóteles en las hojas 36r y 36v.

















