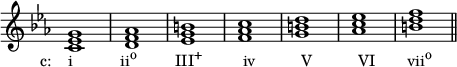Análisis de números romanos

La progresión de acordes vi–ii–V–I en la tonalidad de do mayor. Si se utilizan los nombres de los acordes de la partitura principal, estos acordes podrían denominarse la menor, re menor, sol mayor y do mayor. ^[1]

En teoría musical , el análisis de números romanos es un tipo de análisis armónico en el que los acordes se representan mediante números romanos , que codifican el grado del acorde y la función armónica dentro de una clave musical determinada .

Las convenciones de notación específicas varían: algunos teóricos usan números en mayúsculas (por ejemplo, I, IV, V) para representar acordes mayores y números en minúsculas (por ejemplo, ii, iii, vi) para representar acordes menores . Otros usan números en mayúsculas para todos los acordes independientemente de su calidad . ^[2]

Los números romanos se pueden utilizar para anotar y analizar la progresión armónica de una composición independientemente de su tonalidad específica . Por ejemplo, la omnipresente progresión de blues de doce compases utiliza los acordes tónico (I), subdominante (IV) y dominante (V) construidos sobre los grados primero, cuarto y quinto de la escala respectivamente.

El análisis de los números romanos se basa en la idea de que los acordes pueden representarse y nombrarse por una de sus notas, su raíz (consulte el artículo Historia de la raíz (acorde) para obtener más información). El sistema surgió inicialmente del trabajo y los escritos del bajo fundamental de Rameau .

El primer uso de números romanos se puede encontrar en el primer volumen de Die Kunst des reinen Satzes de Johann Kirnberger en 1774. ^[3] Poco después, el Abbé Georg Joseph Vogler empleó ocasionalmente números romanos en su Grunde der Kuhrpfälzischen Tonschule en 1778 ^{. 4]} También los mencionó en su Handbuch zur Harmonielehre de 1802 y empleó el análisis de números romanos en varias publicaciones desde 1806 en adelante. ^[5]

A la obra de Gottfried Weber, Versuch einer geordneten Theorie der Tonsetzkunst ( Teoría de la composición musical ) (1817-21), se le atribuye a menudo la popularización del método. Más precisamente, introdujo el uso de números grandes en mayúsculas para los acordes mayores, minúsculas en mayúsculas para los menores, superíndice ^o para las quintas disminuidas y 7 discontinuo para las séptimas mayores (véase la figura adjunta). ^[6] Simon Sechter, considerado el fundador de la " teoría de los grados " vienesa ( Stufentheorie ), hizo un uso limitado de los números romanos, siempre en mayúsculas, y a menudo marcaba los fundamentos con notación de letras o con números arábigos. ^[7] Anton Bruckner , que transmitió la teoría a Schoenberg y Schenker , aparentemente no utilizó números romanos en sus clases en Viena. ^[8]

En la teoría musical relacionada con o derivada del período de práctica común , los números romanos se utilizan con frecuencia para designar los grados de la escala , así como los acordes construidos sobre ellos. ^[2] En algunos contextos, sin embargo, se utilizan números arábigos con signos de circunvalación para designar los grados de la escala en sí (por ejemplo,,,, ...).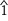

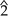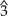Los símbolos básicos de análisis de números romanos que se utilizan comúnmente en textos pedagógicos se muestran en la siguiente tabla. ^{[9] [10] : 71}

Símbolo	Significado	Ejemplos
Número romano en mayúsculas	Tríada mayor	I
Número romano en minúscula	Tríada menor	i
Superíndice +	Tríada aumentada	Yo +
Superíndice o	Tríada disminuida	yo o
Número superíndice	Nota añadida	V 7
Dos o más números ( #-# )	Notación de bajo cifrado	V 4–3
Superíndice # y# #	Primera inversión	Yo 6
	Segunda inversión	I6 4

A continuación se muestran los números romanos para las siete tríadas diatónicas en posición fundamental construidas sobre las notas de la escala de Do mayor.

Además, según Music: In Theory and Practice , "[a]veces es necesario indicar sostenidos, bemoles o naturales por encima de la nota grave". ^{[10] : 74} Las alteraciones accidentales pueden estar debajo de los números en superíndice y subíndice, antes de los números en superíndice y subíndice, o usando una barra (/) o un signo más (+) para indicar que el intervalo está elevado (ya sea ♮ en una tonalidad bemol o ♯ oen una tonalidad sostenida.

Los acordes secundarios se indican con una barra, por ejemplo, V/V.

Los schenkerianos modernos a menudo prefieren el uso de números mayúsculas grandes para todos los grados en todos los modos, de conformidad con el propio uso de Schenker. ^[a]

Los números romanos a veces se complementan con números arábigos para indicar la inversión de los acordes. El sistema es similar al del bajo cifrado , los números arábigos describen el intervalo o intervalos característicos por encima de la nota grave del acorde, y las cifras 3 y 5 suelen omitirse. La primera inversión se denota con el número 6 (por ejemplo, I ⁶ para la primera inversión de la tríada tónica, aunque una cifra completa requeriría I⁶
₃); los numerales⁶
₄denota la segunda inversión (por ejemplo, I⁶
₄). Los acordes de séptima invertida se denotan de manera similar con uno o dos números arábigos que describen los intervalos más característicos, a saber, el intervalo de un segundo entre la séptima y la fundamental: V ⁷ es la séptima dominante (por ejemplo, G–B–D–F); V⁶
₅es su primera inversión (B–D– F–G ); V⁴
₃su segunda inversión (D– F–G –B); y V⁴
₂o V ² su tercera inversión ( F–G –B–D). ^{[10] : 79–80}

En el Reino Unido, existe otro sistema en el que los números romanos se combinan con letras latinas para indicar la inversión. ^[13] En este sistema, se utiliza un sufijo "a" para representar la posición de la raíz, "b" para la primera inversión y "c" para la segunda inversión. Sin embargo, la "a" rara vez se utiliza para indicar la posición de la raíz, al igual que⁵
₃rara vez se utiliza para indicar la posición de la raíz en la nomenclatura estadounidense. ^{[14] [ verificación fallida – ver discusión ] [15] [16] [17]}

En teoría musical, libros falsos y partituras principales dirigidas al jazz y la música popular , muchas melodías y canciones están escritas en una tonalidad y, como tal, para todos los acordes, se da un nombre de letra y símbolos para todas las tríadas (por ejemplo, C, G ⁷ , Dm, etc.). En algunos libros falsos y partituras principales, todas las tríadas pueden representarse con números en mayúsculas, seguidos de un símbolo para indicar si no es un acorde mayor (por ejemplo, "m" para menor o " ^ø " para semidisminuido o "7" para un acorde de séptima). Un número en mayúsculas que no está seguido de un símbolo se entiende como un acorde mayor. El uso de números romanos permite a los intérpretes de la sección rítmica tocar la canción en cualquier tonalidad solicitada por el director de la banda o el cantante principal . Los intérpretes de acompañamiento traducen los números romanos a los acordes específicos que se utilizarían en una tonalidad determinada.

En la tonalidad de mi mayor, los acordes diatónicos son:

• E ^maj7 se convierte en I ^maj7 (también I ^∆7 , o simplemente I)
• F ♯ m ⁷ se convierte en II ^m7 (también II ⁻⁷ , II ^min7 , IIm o II ⁻ )
• G ♯ m ⁷ se convierte en III ^m7 (también III ⁻⁷ , III ^min7 , IIIm o III ⁻ )
• Un ^maj7 se convierte en IV ^maj7 (también IV ^∆7 , o simplemente IV)
• B ⁷ se convierte en V ⁷ (o simplemente V; a menudo V ⁹ o V ¹³ en un contexto de jazz)
• C ♯ m ⁷ se convierte en VI ^m7 (también VI ⁻⁷ , VI ^min7 , VIm o VI ⁻ )
• D ♯ ^ø7 se convierte en VII ^ø7 (también VII ^m7b5 , VII ^-7b5 o VII ^ø )

En la música popular y en la música rock , es habitual "tomar prestado" acordes de la escala paralela menor de una tonalidad mayor. Por ello, en estos géneros, en la tonalidad de mi mayor, se suelen utilizar acordes como re mayor (o ♭ VII), sol mayor ( ♭ III) y do mayor ( ♭ VI). Todos estos acordes se toman prestados de la tonalidad de mi menor. De forma similar, en tonalidades menores, también se pueden "tomar prestados" acordes de la escala paralela mayor. Por ejemplo, en mi menor, el acorde diatónico construido sobre el cuarto grado de la escala es IVm, o la menor. Sin embargo, en la práctica, muchas canciones en mi menor utilizarán IV (la mayor), que se toma prestado de la tonalidad de mi mayor. Sin embargo, tomar prestado del acorde paralelo mayor en una tonalidad menor es mucho menos habitual.

El uso del acorde V7 o V (V dominante 7 o V mayor) es típico en la mayoría de la música jazz y pop, independientemente de si la tonalidad es mayor o menor. Aunque el acorde V no es diatónico en una escala menor, su uso en una tonalidad menor no suele considerarse un "préstamo", dada su prevalencia en estos estilos.

La siguiente tabla muestra los números romanos para los acordes construidos en la escala mayor .

Grado de escala	Tónico	Supertónico	Por medio	Subdominante	Dominante	Submediante	Tono líder
Notación convencional	I	ii	iii	IV	V	vi	vii o
Notación alternativa	I	II	III	IV	V	VI	VII [18]
Símbolo de acorde	Yo mayor	2 minutos	III minutos	IV Mayor	V Mayor (o V 7 )	VI minutos	VII dim (o VII o )

En la tonalidad de Do mayor, estos acordes son

La siguiente tabla muestra los números romanos para los acordes construidos en la escala menor natural .

Grado de escala	Tónico	Supertónico	Por medio	Subdominante	Dominante	Submediante	Subtónico	Tono líder
Notación convencional	i	ii o	♭ III	IV	en	♭ VI	♭ VII	vii o
Notación alternativa	i	ii	iii	IV	en	vi	viii
Símbolo de acorde	Yo min	II tenue	♭ III Agosto (o III Mayor)	IV mín. (o IV mayor)	V min (o V 7 )	♭ VI Mayor	♭ VII Mayor	VII dim (o VII o )

En la tonalidad de do menor (menor natural), estos acordes son

El séptimo grado de la escala se eleva muy a menudo medio tono para formar una nota principal, lo que hace que el acorde dominante (V) sea un acorde mayor (es decir, V mayor en lugar de v menor) y el acorde subtónico (vii), un acorde disminuido (vii ^o , en lugar de ♭ VII). Esta versión de la escala menor se llama escala menor armónica . Esto permite a los compositores tener un acorde dominante (V) y también el acorde de séptima dominante (V7) ambos disponibles para una resolución de cadencia más fuerte en la tonalidad menor, es decir, de V a i menor.

En notación tradicional, las tríadas de los siete modos modernos son las siguientes:

No.	Modo	Tónico	Supertónico	Por medio	Subdominante	Dominante	Submediante	Tono subtónico/ tono principal
1	Jónico (mayor)	I	ii	iii	IV	V	vi	vii o
2	dorio	i	ii	♭ III	IV	en	vi o	♭ VII
3	frigio	i	♭ II	♭ III	IV	V o	♭ VI	♭ vii
4	Lidio	I	II	iii	♯ yo soy	V	vi	viii
5	Mixolidio	I	ii	iii o	IV	en	vi	♭ VII
6	Eólica (menor natural)	i	ii o	♭ III	IV	en	♭ VI	♭ VII
7	Locrio	yo o	♭ II	♭ iii	IV	♭ V	♭ VI	♭ vii