Efectos no lineales

En la síntesis enantioselectiva , un efecto no lineal se refiere a un proceso en el que la enantiopureza del catalizador o del auxiliar quiral no se corresponde con la enantiopureza del producto producido. Por ejemplo: se esperaría que un catalizador racémico convierta un sustrato proquiral en un producto racémico (un efecto lineal), pero este no siempre es el caso y se puede producir en su lugar un producto enriquecido quiralmente (un efecto no lineal). [1] [2]

Esto se puede expresar matemáticamente , como se muestra en la ecuación 1. La estereoselección que es mayor o menor que el exceso enantiomérico del catalizador se considera un comportamiento no ideal. En el comportamiento no ideal, esta desviación de la linealidad se describe como el efecto no lineal , NLE . [3]

mi mi producto = mi mi máximo mi mi catalizador {\displaystyle ee_{\text{producto}}=ee_{\max }ee_{\text{catalizador}}}

En el caso de una reacción asimétrica ideal , el producto ee puede describirse como el producto de ee max multiplicado por el catalizador ee . Este no es el caso de las reacciones que presentan NLE. [4]

Los efectos no lineales surgen a menudo en reacciones con una composición de catalizador escalémico. [3] Como observaron por primera vez Wynberg y Feringa en 1976, diferentes enantiómeros de los catalizadores quirales forman complejos heteroquirales, más específicamente agregados de alto orden o formas diméricas del catalizador. [5] Estos complejos heteroquirales influyen en la estereoinducción efectiva de un catalizador escalémico. Las fuentes adicionales de efectos no lineales incluyen la autocatálisis, el proceso en el que la reacción se cataliza a sí misma. [6] Las definiciones generales y los modelos matemáticos son clave para comprender los efectos no lineales y su aplicación a reacciones químicas específicas. En las últimas dos décadas, el estudio de los efectos no lineales ha demostrado dilucidar el mecanismo de reacción y guiar en aplicaciones sintéticas.

Tipos de efectos no lineales

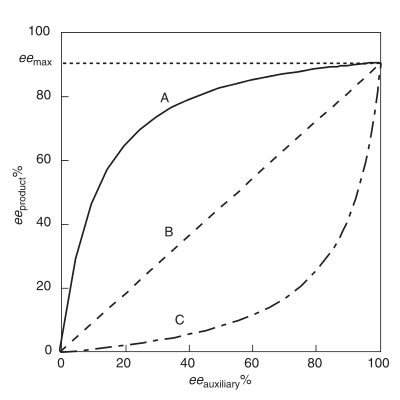
La relación entre el producto ee y el catalizador ee en los escenarios (+)-NLE, lineal y (−)-NLE. [3]

Efecto no lineal positivo, (+)-NLE

Un efecto no lineal positivo , (+)-NLE , está presente en una reacción asimétrica que demuestra un producto ee ( producto ee ) más alto que el predicho por una situación lineal ideal (Figura 1). [4] A menudo se lo denomina amplificación asimétrica , un término acuñado por Oguni y colaboradores. [4] Un ejemplo de un efecto no lineal positivo se observa en el caso de la epoxidación de Sharpless con el sustrato geraniol . [7] En todos los casos de reactividad química que exhiben (+)-NLE, existe una compensación innata entre la velocidad de reacción general y la enantioselectividad. La velocidad general es más lenta y la enantioselectividad es mayor en relación con una reacción de comportamiento lineal.

Efecto no lineal negativo, (−)-NLE

Conocido como agotamiento asimétrico , un efecto no lineal negativo está presente cuando el producto ee es menor que el predicho por una situación lineal ideal. [3] A diferencia de un (+)-NLE, un (−)-NLE da como resultado una velocidad de reacción general más rápida y una disminución en la enantioselectividad. Sintéticamente, un efecto (−)-NLE podría ser beneficioso con un ensayo razonable para separar los enantiómeros del producto y es necesario un alto rendimiento. Se ha informado de un ejemplo interesante de un efecto (−)-NLE en oxidaciones asimétricas de sulfuro . [8]

Modelado de efectos no lineales

En 1986, Henri B. Kagan y sus colaboradores observaron una serie de reacciones conocidas que seguían un comportamiento no ideal. Se adaptó un factor de corrección, f , a la ecuación 1 para ajustar el comportamiento cinético de las reacciones con NLE (ecuación 2). [3]

mi mi producto = F mi mi máximo mi mi catalizador {\displaystyle ee_{\text{producto}}=f\,ee_{\max }ee_{\text{catalizador}}}

Ecuación 2: Una ecuación matemática general que describe el comportamiento no lineal [9]

Lamentablemente, la ecuación 2 es demasiado general para aplicarla a reacciones químicas específicas. Debido a esto, Kagan y sus colaboradores también desarrollaron modelos matemáticos simplificados para describir el comportamiento de los catalizadores que conducen a efectos no lineales. [3] Estos modelos involucran especies genéricas de ML n , basadas en un metal (M) unido a un número n de ligandos enantioméricos (L). El tipo de modelo de ML n varía entre reacciones asimétricas, en función de la bondad del ajuste con los datos de reacción. Con un modelado preciso, la NLE puede dilucidar los detalles mecanísticos de una reacción catalítica enantioselectiva. [8]

Ml2modelo

Descripción general

El modelo más simple para describir un efecto no lineal, el modelo ML 2 involucra un sistema metálico (M) con dos ligandos quirales, L R y L S . Además de la reacción catalizada de interés, el modelo tiene en cuenta un equilibrio en estado estacionario entre los complejos catalíticos no unidos y unidos. [3] Hay tres posibles complejos catalíticos en equilibrio (ML S L R , ML S L S , ML R L R ). Los dos complejos enantioméricamente puros ( ML S L S , ML R L R ) se denominan complejos homoquirales . [3] El posible complejo heteroquiral , ML R L S , a menudo se denomina mesocomplejo. [3]

METRO + yo R + yo S ⇌ METRO yo R yo R + METRO yo S yo S + METRO yo R yo S incógnita y el } concentraciones ↓ a R R ↓ a S S ↓ a R S } tarifas productos de reacción es producto Constante de equilibrio:  K = el 2 incógnita y {\displaystyle {\begin{aligned}&{\begin{matrix}\mathrm {M} +\mathrm {L} _{R}+\mathrm {L} _{S}\quad \rightleftharpoons \quad &\mathrm {ML} _{R}\mathrm {L} _{R}&+&\mathrm {ML} _{S}\mathrm {L} _{S}&+&\mathrm {ML} _{R}\mathrm {L} _{S}&\\&x&&y&&z&\left\}\quad {\overset {}{\text{concentrations}}}\right.\\&\\&\left\downarrow {\begin{matrix}\\\mathrm {r} _{RR}\\\\\end{matrix}}\right.&&\left\downarrow {\begin{matrix}\\\mathrm {r} _{SS}\\\\\end{matrix}}\right.&&\left\downarrow {\begin{matrix}\\\mathrm {r} _{RS}\\\\\end{matrix}}\right.&\left\}\quad {\overset {}{\text{rates}}}\right.\qquad \qquad \\\end{matrix}}\\\\&\qquad \qquad \qquad \qquad \qquad \qquad \;\;\;\;\;{\text{reaction products}}\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \;\;\;\;\;{\text{ee}}_{\text{product}}\\\\&{\text{Equilibrium constant: }}K={\frac {z^{2}}{xy}}\end{aligned}}}
El esquema básico de un modelo ML 2 desarrollado por HB Kagan [8]

La constante de equilibrio que describe este equilibrio, K, es presumiblemente independiente de la reacción química catalítica. En el modelo de Kagan, K está determinada por la cantidad de agregación presente en el entorno químico. Se considera que AK=4 es el estado en el que hay una distribución estadística de ligandos para cada complejo metálico. [3] En otras palabras, no hay ninguna desventaja o ventaja termodinámica en la formación de complejos heteroquirales en K=4. [4]

Obedeciendo la misma ley de velocidad cinética , cada uno de los tres complejos catalíticos cataliza la reacción deseada para formar el producto. [8] Como enantiómeros entre sí, los complejos homoquirales catalizan la reacción a la misma velocidad, aunque se induce una configuración absoluta opuesta del producto (es decir, r RR =r SS ). El complejo heteroquiral, sin embargo, forma un producto racémico a una constante de velocidad diferente (es decir, r RS ). [9]

Modelo matemático para el ML2Modelo

Para describir el modelo ML 2 en parámetros cuantitativos, Kagan y colaboradores describieron la siguiente fórmula:

e e product = e e max e e auxiliary ( 1 + β ) / ( 1 + g β ) {\displaystyle ee_{\text{product}}=ee_{\text{max}}ee_{\text{auxiliary}}(1+\beta )/(1+g\,\beta )}

En el factor de corrección, Kagan y colaboradores introdujeron dos nuevos parámetros ausentes en la Ecuación 1, β y g. [9] En general, estos parámetros representan la concentración y actividad de tres complejos catalíticos entre sí. β representa la cantidad relativa del complejo heteroquiral (ML R L S ) como se muestra en la Ecuación 3. [3] Es importante reconocer que la constante de equilibrio K es independiente tanto de β como de g. [8] Como lo describe Donna Blackmond en Scripps Research Institute, "el parámetro K es una propiedad inherente de la mezcla de catalizador, independiente del catalizador ee . K también es independiente de la reacción catalítica en sí y, por lo tanto, independiente del parámetro g".

β = z / ( x + y ) {\displaystyle \beta =z/(x+y)}

Ecuación 3: El factor de corrección, β, puede describirse como z, la concentración del complejo heteroquiral, dividida por x e y, las concentraciones respectivas de la concentración del complejo dividida por x e y, las concentraciones respectivas de los complejos homoquirales [3]

El parámetro g representa la reactividad del complejo heteroquiral en relación con los complejos homoquirales. Como se muestra en la ecuación 5, esto se puede describir en términos de constantes de velocidad. Dado que los complejos homoquirales reaccionan a velocidades idénticas, g se puede describir como la constante de velocidad correspondiente al complejo heteroquiral dividida por la constante de velocidad correspondiente a cualquiera de los complejos homoquirales.

g = r r s / r r r {\displaystyle g=r_{rs}/r_{rr}}

Ecuación 4: El parámetro de corrección, g, se puede describir como la tasa de formación del producto con el catalizador heteroquiral ML R L S dividida por la tasa de formación del producto del complejo homoquiral (ML R L R o ML S L S ).

Interpretación de los resultados matemáticos del ML2Modelo

  • Si β=0 o g=1, la ecuación ML 2 se simplifica a la ecuación 1. No hay ningún complejo de catalizador meso presente o activo. Por lo tanto, las propiedades aditivas simples deberían aplicarse a tal escenario para establecer una relación lineal entre la enantioselectividad del producto y la enantiopureza del catalizador quiral.
  • Si el factor de corrección es mayor que uno, la reacción muestra una amplificación asimétrica , también conocida como efecto no lineal positivo. Bajo el modelo ML 2 , un (+)-NLE infiere un catalizador heteroquiral menos reactivo. En este caso, la constante de equilibrio K también aumenta a medida que aumenta el factor de corrección. Aunque la enantioselectividad del producto es relativamente alta en comparación con la enantiopureza del catalizador quiral, esto tiene un costo en la velocidad de reacción general. Para lograr una amplificación asimétrica, debe haber una concentración relativamente grande del complejo heteroquiral. Además, este complejo heteroquiral debe tener una tasa de reactividad sustancialmente más lenta, r RS . Por lo tanto, las especies catalíticas reactivas deben disminuir en concentración, lo que lleva a una velocidad de reacción general más lenta.
  • Si el factor de corrección es menor que uno, la reacción muestra un agotamiento asimétrico, también conocido como efecto no lineal negativo. En este escenario, el catalizador heteroquiral es relativamente más reactivo que los complejos catalíticos homoquirales. En este caso, el (−)-NLE puede dar como resultado una formación de producto más rápida, aunque menos selectiva.

iv. Cinética de la reacción con el modelo ML 2 : tras la publicación del modelo ML 2 por parte de HB Kagan , la profesora Donna Blackmond de Scripps demostró cómo se podía utilizar este modelo para calcular también las velocidades de reacción generales. Con estas velocidades de reacción relativas, Blackmond demostró cómo se podía utilizar el modelo ML 2 para formular predicciones cinéticas que luego se podían comparar con datos experimentales. La ecuación de velocidad general, ecuación 6, se muestra a continuación. [8]

r = ( x + y + g z ) r R R {\displaystyle r=(x+y+gz)r_{RR}}

Además de la bondad del ajuste al modelo, la información cinética sobre la reacción general puede validar aún más el mecanismo de reacción propuesto. Por ejemplo, un NLE positivo en el ML 2 debería dar como resultado una velocidad de reacción general más baja. [8] Al resolver la velocidad de reacción a partir de la ecuación 6, se puede confirmar si ese es el caso.

M*l2Modelo

Descripción general

Similar al modelo ML 2 , este sistema modificado implica ligandos quirales que se unen a un centro metálico (M) para crear un nuevo centro de quiralidad. [4] Hay cuatro pares de complejos quirales enantioméricos en el modelo M*L 2 , como se muestra en la Figura 5.

M + L R + L S ⇌⇌ M R L R L R + M R L R L S + M R L S L R + M R L S L S M S L S L S + M S L S L R + M S L R L S + M S L R L R ↓ k 0 ± E E 0 ↓ k 1 ± E E 1 ↓ k 2 ± E E 2 ↓ k 3 ± E E 3 products {\displaystyle {\begin{matrix}{\begin{matrix}\mathrm {M} +\mathrm {L} _{R}+\mathrm {L} _{S}\quad \rightleftharpoons \rightleftharpoons \quad \\\\\\\\\\&\end{matrix}}{\begin{aligned}&{\begin{matrix}\mathrm {M} _{R}\mathrm {L} _{R}\mathrm {L} _{R}&+&\mathrm {M} _{R}\mathrm {L} _{R}\mathrm {L} _{S}&+&\mathrm {M} _{R}\mathrm {L} _{S}\mathrm {L} _{R}&+&\mathrm {M} _{R}\mathrm {L} _{S}\mathrm {L} _{S}\\\mathrm {M} _{S}\mathrm {L} _{S}\mathrm {L} _{S}&+&\mathrm {M} _{S}\mathrm {L} _{S}\mathrm {L} _{R}&+&\mathrm {M} _{S}\mathrm {L} _{R}\mathrm {L} _{S}&+&\mathrm {M} _{S}\mathrm {L} _{R}\mathrm {L} _{R}\\&\\\left\downarrow {\begin{matrix}k_{0}\\\pm EE_{0}\end{matrix}}\right.&&\left\downarrow {\begin{matrix}k_{1}\\\pm EE_{1}\end{matrix}}\right.&&\left\downarrow {\begin{matrix}k_{2}\\\pm EE_{2}\end{matrix}}\right.&&\left\downarrow {\begin{matrix}k_{3}\\\pm EE_{3}\end{matrix}}\right.\end{matrix}}\\\\&\qquad \qquad \qquad \qquad \qquad \,\,\,\,{\text{products}}\end{aligned}}\end{matrix}}}
Figura 5: El equilibrio presente en el modelo M*L 2 . Es muy similar al modelo ML 2 . Sin embargo, debido al nuevo centro de quiralidad, hay cuatro conjuntos de enantiómeros.

En este modelo, se puede hacer la aproximación de que los complejos diméricos se disocian irreversiblemente en las especies monoméricas . En este caso, se aplican las mismas ecuaciones matemáticas que se aplicaron al modelo ML* 2 .

Ml3modelo

Descripción general

Un nivel superior de modelado, el modelo ML 3 involucra cuatro complejos catalíticos activos: ML R L R L R , ML S L S L S , ML R L R L S , ML S L S L R . A diferencia del modelo ML 2 , donde solo los dos complejos homoquirales reaccionaron para formar un producto enriquecido enantioméricamente, los cuatro complejos catalíticos reaccionan enantioselectivamente. Sin embargo, la misma suposición de estado estable se aplica al equilibrio entre complejos catalíticos no unidos y unidos como en el modelo ML 2 más simple . Esta relación se muestra a continuación en la Figura 7.

M + L R + L S ↽ − − ⇀   ML R L R L R ⏟ x + ML S L S L S ⏟ y + ML R L R L S ⏟ z + ML S L S L R ⏟ w {\displaystyle {\ce {{M}+{L_{R}}+L_{S}<=>}}\ \underbrace {\ce {ML_{R}L_{R}L_{R}}} _{x}+\underbrace {\ce {ML_{S}L_{S}L_{S}}} _{y}+\underbrace {\ce {ML_{R}L_{R}L_{S}}} _{z}+\underbrace {\ce {ML_{S}L_{S}L_{R}}} _{w}}
Figura 7: El equilibrio entre las especies no ligadas y las especies catalíticas reactivas en el modelo ML 3 .

Modelado matemático

Calcular el producto ee es considerablemente más complicado que en el modelo ML 2 simple . Cada uno de los dos complejos catalíticos heteroquirales debería reaccionar a la misma velocidad. Los complejos catalíticos homoquirales, de forma similar al caso ML 2 , también deberían reaccionar a la misma velocidad. Por lo tanto, el parámetro de corrección g todavía se calcula como la velocidad del complejo catalítico heteroquiral dividida por la velocidad del complejo catalítico homoquiral. Sin embargo, dado que los complejos heteroquirales dan lugar a un producto enantioméricamente enriquecido, la ecuación general para calcular el producto ee se vuelve más difícil. En la Figura 8, se muestra la fórmula matemática para calcular la enantioselectividad.

E E prod = E E 0 e e aux 3 + 3 g E E 0 ′ / E E 0 + ( 1 − 3 g E E 0 ′ / E E 0 ) e e aux 2 1 + 3 g + 3 ( 1 − g ) e e aux 2 {\displaystyle EE_{\text{prod}}=EE_{0}ee_{\text{aux}}{\frac {3+3\,g\,EE'_{0}/EE_{0}+(1-3\,g\,EE'_{0}/EE_{0})ee_{\text{aux}}^{2}}{1+3\,g+3(1-g)ee_{\text{aux}}^{2}}}}

Figura 8: Fórmula matemática que describe un sistema ML 3. El producto ee se calcula multiplicando el ee max por el factor de corrección desarrollado por Kagan y colaboradores. [4]

Interpretación del ML3Modelo

En general, interpretar los valores del parámetro de corrección de g para predecir efectos no lineales positivos y negativos es considerablemente más difícil. En el caso en que los complejos heteroquirales ML R L R L S y ML S L S L R son menos reactivos que los complejos homoquirales ML S L S L S y ML R L R L R , se observa un comportamiento cinético similar al modelo ML 2 (Figura 9). Sin embargo, se observa un comportamiento sustancialmente diferente en el caso en que los complejos heteroquirales son más reactivos que los complejos homoquirales. En tal caso, Kagan y colaboradores demostraron que es posible tener un caso “ en el que el exceso enantiomérico podría asumir valores mucho mayores para un ligando parcialmente resuelto que para un ligando enantioméricamente puro ”. Los autores propusieron el término “ efecto no lineal hiperpositivo ” para caracterizar esta situación.

Figura 9: Cuando los complejos heteroquirales son más selectivos y reactivos que los complejos homoquirales. [4]
Figura 10: Cuando los complejos homoquirales son más selectivos y reactivos que los complejos heteroquirales. [4]

Efecto reservorio

Descripción general

El efecto de reservorio, que a menudo se describe de forma adyacente o en colaboración con el modelo ML 2 , describe el escenario en el que parte del ligando quiral se asigna a un grupo de complejos catalíticos heteroquirales inactivos fuera del ciclo catalítico. [4] Un grupo de catalizadores heteroquirales no reactivos, descrito con un grupo ee , desarrolla un equilibrio con los complejos homoquirales catalíticamente activos, descritos con un ee efectivo . [8] Dependiendo de la concentración del grupo inactivo de catalizadores, se puede calcular la enantiopureza de los complejos catalizadores activos. El resultado general del efecto de reservorio es una amplificación asimétrica, también conocida como (+)-NLE. [3]

Origen del efecto reservorio

La acumulación de complejos catalíticos no reactivos, como se describe en el efecto de reservorio, puede ser el resultado de varios factores. Uno de ellos podría ser un efecto de agregación entre los complejos catalíticos heteroquirales que tiene lugar antes del equilibrio en estado estacionario. [3]

Primeros ejemplos del efecto no lineal

Epoxidación sin agudeza del geraniol

En 1986, Kagan y sus colaboradores pudieron demostrar la no linealidad con la epoxidación de Sharpless de (E)-geraniol (Figura 11). Bajo condiciones de oxidación de Sharpless con Ti(Oi-Pr) 4 /(+)-DET/t-BuOOH, Kagan y sus colaboradores pudieron demostrar que había una correlación no lineal entre el producto de ee y el ee del catalizador quiral, tartrato de dietilo (DET). [3] Como se puede ver en la Figura 11, se observó un producto de ee mayor que el esperado. De acuerdo con el modelo ML 2 , Kagan y sus colaboradores pudieron concluir que estaba presente un complejo DET heteroquiral menos reactivo. Esto explicaría por lo tanto la amplificación asimétrica observada. Los datos de la no linealidad también son consistentes con el mecanismo de Sharpless de epoxidación asimétrica. [10]

Figura 11: Esquema de reacción general estudiado por Kagan y colaboradores para la epoxidación de Sharpless del geraniol. [10]

Oxidación asimétrica de sulfuro

En 1994, Kagan y sus colaboradores informaron de un NLE en la oxidación asimétrica de sulfuros. La bondad de ajuste de los datos de reacción coincidió con el modelo ML 4. Esto implicaba que un titanio dimérico complejado con 4 ligandos DET era la especie catalítica activa. [3] En este caso, la velocidad de reacción sería significativamente más rápida en relación con la cinética de reacción ideal. La desventaja, como es el caso en todos los escenarios de (−)-NLE, es que la enantioselectividad fue menor de lo esperado. [3] A continuación, en la Figura 12, se puede ver que la concavidad de los puntos de datos es altamente indicativa de un (−)-NLE. [1]

Figura 12: Una clara indicación de un efecto no lineal negativo en la reacción de oxidación asimétrica de sulfuro. [1]

Catálisis prebiótica y efecto no lineal

En la química prebiótica , los sistemas autocatalíticos juegan un papel importante en la comprensión del origen de la quiralidad en la vida. [6] Una reacción autocatalítica, una reacción en la que el producto actúa como catalizador de sí mismo, sirve como modelo para la homoquiralidad . La reacción asimétrica de Soai se conoce comúnmente como plausibilidad química para esta hipótesis prebiótica. En este sistema, se observa una amplificación asimétrica durante el proceso de catálisis autocatalítica. La profesora Donna Blackmond ha estudiado la NLE de esta reacción ampliamente utilizando el modelo ML 2 de Kagan . A partir de este análisis matemático, Blackmond pudo concluir que un complejo dimérico homoquiral era el catalizador activo en la promoción de la homoquiralidad para la reacción de Soai. [3] [6]

Notas

  1. ^ abc Guillaneux, Denis; Zhao, Shu-Hai; Samuel, Odile; Rainford, David; Kagan, Henri B. (octubre de 1994). "Efectos no lineales en catálisis asimétrica". Revista de la Sociedad Química Americana . 116 (21): 9430–9439. doi :10.1021/ja00100a004.
  2. ^ Satyanarayana, Tummanapalli; Abraham, Susan; Kagan, Henri B. (5 de enero de 2009). "Efectos no lineales en catálisis asimétrica". Edición internacional Angewandte Chemie . 48 (3): 456–494. doi :10.1002/anie.200705241. PMID  19115268.
  3. ^ abcdefghijklmnopqr Blackmond, Donna G. (diciembre de 1997). "Modelos matemáticos de efectos no lineales en catálisis asimétrica: nuevos conocimientos basados ​​en el papel de la velocidad de reacción". Journal of the American Chemical Society . 119 (52): 12934–12939. doi :10.1021/ja973049m.
  4. ^ abcdefghi Girard, Christian; Kagan, Henri B. (16 de noviembre de 1998). "Efectos no lineales en la síntesis asimétrica y las reacciones estereoselectivas: diez años de investigación". Angewandte Chemie International Edition . 37 (21): 2922–2959. doi : 10.1002/(SICI)1521-3773(19981116)37:21<2922::AID-ANIE2922>3.0.CO;2-1 . PMID  29711141.
  5. ^ Wynberg, Hans; Feringa, Ben (enero de 1976). "Reconocimiento e interacciones enantioméricas" (PDF) . Tetrahedron . 32 (22): 2831–2834. doi :10.1016/0040-4020(76)80131-7.
  6. ^ abc Blackmond, DG (5 de abril de 2004). "Asymmetric Catalysis Special Feature Part II: Asymmetric autocatalysis and its implications for the origin of homoquirality" (Artículo especial sobre catálisis asimétrica, parte II: autocatálisis asimétrica y sus implicaciones para el origen de la homoquiralidad). Actas de la Academia Nacional de Ciencias . 101 (16): 5732–5736. Bibcode :2004PNAS..101.5732B. doi : 10.1073/pnas.0308363101 . PMC 395976 . PMID  15067112. 
  7. ^ Puchot, C.; Samuel, O.; Dunach, E.; Zhao, S.; Agami, C.; Kagan, HB (abril de 1986). "Efectos no lineales en la síntesis asimétrica. Ejemplos en oxidaciones asimétricas y reacciones de aldolización". Revista de la Sociedad Química Americana . 108 (9): 2353–2357. doi :10.1021/ja00269a036. PMID  22175583.
  8. ^ abcdefgh Blackmond, Donna G. (junio de 2000). "Aspectos cinéticos de los efectos no lineales en la catálisis asimétrica". Accounts of Chemical Research . 33 (6): 402–411. doi :10.1021/ar990083s. PMID  10891058.
  9. ^ abc Kagan, Henri B. (2001). "Efectos no lineales en la catálisis asimétrica: un relato personal". Synlett . 2001 (Número especial): 0888–0899. doi : 10.1055/s-2001-14660 .
  10. ^ ab Finn, MG; Sharpless, K. Barry (enero de 1991). "Mecanismo de epoxidación asimétrica. 2. Estructura del catalizador". Revista de la Sociedad Química Americana . 113 (1): 113–126. doi :10.1021/ja00001a019.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Non-linear_effects&oldid=1251177760"