Fuerza neta

En mecánica , la fuerza neta es la suma de todas las fuerzas que actúan sobre un objeto. Por ejemplo, si dos fuerzas actúan sobre un objeto en direcciones opuestas y una es mayor que la otra, las fuerzas pueden reemplazarse por una sola fuerza que es la diferencia entre la fuerza mayor y la menor. Esa fuerza es la fuerza neta. ^[1]

Cuando las fuerzas actúan sobre un objeto, modifican su aceleración . La fuerza neta es el efecto combinado de todas las fuerzas sobre la aceleración del objeto, como se describe en la segunda ley del movimiento de Newton .

Cuando la fuerza neta se aplica en un punto específico sobre un objeto, se puede calcular el par asociado. La suma de la fuerza neta y el par se denomina fuerza resultante , que hace que el objeto gire de la misma manera que lo harían todas las fuerzas que actúan sobre él si se aplicaran individualmente. ^[2]

Es posible que todas las fuerzas que actúan sobre un objeto no produzcan ningún par de torsión. Esto sucede cuando la fuerza neta se aplica a lo largo de la línea de acción .

En algunos textos, los términos fuerza resultante y fuerza neta se utilizan como si significaran lo mismo. Esto no siempre es así, especialmente en temas complejos como el movimiento de objetos giratorios o situaciones en las que todo está perfectamente equilibrado, conocido como equilibrio estático . En estos casos, es importante entender que "fuerza neta" y "fuerza resultante" pueden tener significados distintos.

En física, una fuerza se considera una cantidad vectorial . Esto significa que no solo tiene un tamaño (o magnitud), sino también una dirección en la que actúa. Normalmente representamos la fuerza con el símbolo F en negrita o, a veces, colocamos una flecha sobre el símbolo para indicar su naturaleza vectorial, como esto: .${\displaystyle \mathbf {F}}$

Cuando necesitamos representar visualmente una fuerza, dibujamos un segmento de línea. Este segmento comienza en un punto A , donde se aplica la fuerza, y termina en otro punto B . Esta línea no solo nos da la dirección de la fuerza (de A a B ) sino también su magnitud: cuanto más larga sea la línea, más intensa será la fuerza.

Uno de los conceptos esenciales de la física es que las fuerzas se pueden sumar, lo que constituye la base de la suma de vectores. Este concepto ha sido fundamental para la física desde los tiempos de Galileo y Newton, y constituye la piedra angular del cálculo vectorial , que cobró importancia a fines del siglo XIX y principios del XX. ^[3]

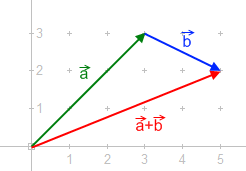
La imagen de la derecha muestra cómo sumar dos fuerzas utilizando el método de "punta a cola". Este método implica dibujar las fuerzas , y desde la punta de la primera fuerza. La fuerza resultante, o fuerza "total", , se dibuja luego desde el comienzo de la primera fuerza (la cola) hasta el final de la segunda fuerza (la punta). Comprender este concepto es fundamental para entender cómo interactúan las fuerzas y se combinan para influir en el movimiento y el equilibrio de los objetos. ${\displaystyle {\mathbf {\mathbf {a}}}$${\displaystyle {\mathbf {\mathbf {b} }}}$${\displaystyle \mathbf {F} _{t}={\mathbf {\mathbf {a} }}+{\mathbf {\mathbf {b} }}}$

Cuando se aplican fuerzas a un cuerpo extenso (un cuerpo que no es un único punto), se pueden aplicar en diferentes puntos. Estas fuerzas se denominan "vectores ligados". Es importante recordar que, para sumar estas fuerzas, es necesario considerarlas en el mismo punto.

El concepto de "fuerza neta" entra en juego cuando se observa el efecto total de todas estas fuerzas sobre el cuerpo. Sin embargo, la fuerza neta por sí sola no necesariamente preserva el movimiento del cuerpo. Esto se debe a que, además de la fuerza neta, también importa el "par" o efecto rotacional asociado con estas fuerzas. La fuerza neta debe aplicarse en el punto correcto y con el par asociado correcto para replicar el efecto de las fuerzas originales.

Cuando la fuerza neta y el par de torsión apropiado se aplican en un único punto, juntos constituyen lo que se conoce como fuerza resultante . Esta combinación de fuerza y ​​par de torsión resultante tendrá el mismo efecto sobre el cuerpo que todas las fuerzas originales y sus pares de torsión asociados.

Una fuerza se conoce como un vector límite, lo que significa que tiene una dirección, una magnitud y un punto de aplicación . Una forma conveniente de definir una fuerza es mediante un segmento de línea desde un punto A hasta un punto B. Si denotamos las coordenadas de estos puntos como A = (A _x , A _y , A _z ) y B = (B _x , B _y , B _z ), entonces el vector de fuerza aplicado en A está dado por

${\displaystyle \mathbf {F} =\mathbf {B} -\mathbf {A} =(B_{x}-A_{x},B_{y}-A_{y},B_{z}-A_{z }).}$

La longitud del vector define la magnitud de y está dada por${\displaystyle \mathbf {\mathbf {B}} -\mathbf {\mathbf {A}} }$${\displaystyle \mathbf {\mathbf {F}} }$

${\displaystyle |\mathbf {F} |={\sqrt {(B_{x}-A_{x})^{2}+(B_{y}-A_{y})^{2}+(B_{ z}-A_{z})^{2}}}.}$

La suma de dos fuerzas F ₁ y F ₂ aplicadas en A se puede calcular a partir de la suma de los segmentos que las definen. Sea F ₁  =  B − A y F ₂  =  D − A , entonces la suma de estos dos vectores es

${\displaystyle \mathbf {F} =\mathbf {F} _{1}+\mathbf {F} _{2}=\mathbf {B} -\mathbf {A} +\mathbf {D} -\mathbf { A} ,}$

que puede escribirse como

${\displaystyle \mathbf {F} =\mathbf {F} _{1}+\mathbf {F} _{2}=2\left({\frac {\mathbf {B} +\mathbf {D} }{2}}-\mathbf {A} \right)=2(\mathbf {E} -\mathbf {A} ),}$

donde E es el punto medio del segmento BD que une los puntos B y D.

Por lo tanto, la suma de las fuerzas F ₁ y F ₂ es el doble del segmento que une A con el punto medio E del segmento que une los puntos extremos B y D de las dos fuerzas. La duplicación de esta longitud se logra fácilmente definiendo los segmentos BC y DC paralelos a AD y AB , respectivamente, para completar el paralelogramo ABCD . La diagonal AC de este paralelogramo es la suma de los dos vectores de fuerza. Esto se conoce como la regla del paralelogramo para la adición de fuerzas.

Cuando una fuerza actúa sobre una partícula, se aplica sobre un único punto (el volumen de la partícula es despreciable): se trata de una fuerza puntual y la partícula es su punto de aplicación. Pero una fuerza externa sobre un cuerpo extenso (objeto) puede aplicarse sobre varias de sus partículas constituyentes, es decir, puede "distribuirse" sobre algún volumen o superficie del cuerpo. Sin embargo, para determinar su efecto rotacional sobre el cuerpo es necesario especificar su punto de aplicación (en realidad, la línea de aplicación, como se explica a continuación). El problema suele resolverse de las siguientes formas:

• A menudo, el volumen o la superficie sobre la que actúa la fuerza es relativamente pequeño en comparación con el tamaño del cuerpo, de modo que se puede aproximar mediante un punto. Por lo general, no es difícil determinar si el error causado por dicha aproximación es aceptable.
• Si no es aceptable (por ejemplo, en el caso de la fuerza gravitatoria), dicha fuerza de "volumen/superficie" se debe describir como un sistema de fuerzas (componentes), cada una de las cuales actúa sobre una sola partícula, y luego se debe realizar el cálculo para cada una de ellas por separado. Este cálculo se simplifica típicamente mediante el uso de elementos diferenciales del volumen/superficie del cuerpo y el cálculo integral. Sin embargo, en varios casos se puede demostrar que dicho sistema de fuerzas se puede reemplazar por una única fuerza puntual sin el cálculo real (como en el caso de la fuerza gravitatoria uniforme).

En cualquier caso, el análisis del movimiento de un cuerpo rígido comienza con el modelo de fuerza puntual. Y cuando se representa gráficamente una fuerza que actúa sobre un cuerpo, el segmento de línea orientado que representa la fuerza suele dibujarse de forma que "comience" (o "termine") en el punto de aplicación.

En el ejemplo que se muestra en el diagrama opuesto, una sola fuerza actúa en el punto de aplicación H sobre un cuerpo rígido libre. El cuerpo tiene la masa y su centro de masa es el punto C. En la aproximación de masa constante, la fuerza provoca cambios en el movimiento del cuerpo descritos por las siguientes expresiones:${\displaystyle \mathbf {F}}$${\estilo de visualización m}$

${\displaystyle \mathbf {a} ={\mathbf {F} \sobre m}}$   es el centro de aceleración de masas; y

${\displaystyle \mathbf {\alpha } ={\mathbf {\tau } \sobre I}}$   es la aceleración angular del cuerpo.

En la segunda expresión, es el momento de torsión o momento de fuerza, mientras que es el momento de inercia del cuerpo. Un momento de torsión causado por una fuerza es una cantidad vectorial definida con respecto a un punto de referencia:${\displaystyle \mathbf {\tau}}$${\displaystyle I}$${\displaystyle \mathbf {F}}$

${\displaystyle \mathbf {\tau} =\mathbf {r} \times \mathbf {F}}$   es el vector de par, y

${\displaystyle \ \tau =Fk}$   es la cantidad de torque.

El vector es el vector de posición del punto de aplicación de la fuerza y, en este ejemplo, se dibuja a partir del centro de masas como punto de referencia (ver diagrama). El segmento de línea recta es el brazo de palanca de la fuerza con respecto al centro de masas. Como sugiere la ilustración, el par no cambia (el mismo brazo de palanca) si el punto de aplicación se mueve a lo largo de la línea de aplicación de la fuerza (línea negra punteada). De manera más formal, esto se desprende de las propiedades del producto vectorial y muestra que el efecto rotacional de la fuerza depende solo de la posición de su línea de aplicación y no de la elección particular del punto de aplicación a lo largo de esa línea.${\displaystyle \mathbf {r}}$${\estilo de visualización k}$${\displaystyle \mathbf {F}}$

El vector de par es perpendicular al plano definido por la fuerza y ​​el vector , y en este ejemplo está dirigido hacia el observador; el vector de aceleración angular tiene la misma dirección. La regla de la mano derecha relaciona esta dirección con la rotación en sentido horario o antihorario en el plano del dibujo.${\displaystyle \mathbf {r}}$

El momento de inercia se calcula con respecto al eje que pasa por el centro de masas y que es paralelo al momento de torsión. Si el cuerpo que se muestra en la ilustración es un disco homogéneo, este momento de inercia es . Si el disco tiene una masa de 0,5 kg y un radio de 0,8 m, el momento de inercia es 0,16 kgm ² . Si la magnitud de la fuerza es 2 N y el brazo de palanca 0,6 m, la magnitud del momento de torsión es 1,2 Nm. En el instante mostrado, la fuerza imparte al disco la aceleración angular α = τ /I = 7,5 rad/s ² , y a su centro de masas imparte la aceleración lineal a  = F / m  = 4 m/s ² .${\displaystyle I}$${\displaystyle I=mr^{2}/2}$

La fuerza y ​​el par resultantes sustituyen los efectos de un sistema de fuerzas que actúan sobre el movimiento de un cuerpo rígido. Un caso particular interesante es una resultante sin par, que se puede hallar de la siguiente manera:

1. La suma vectorial se utiliza para encontrar la fuerza neta;
2. Utilice la ecuación para determinar el punto de aplicación con torque cero:

${\displaystyle \mathbf {r} \times \mathbf {F} _{\mathrm {R} }=\sum _{i=1}^{N}(\mathbf {r} _{i}\times \mathbf {F} _ {i})}$

donde es la fuerza neta, ubica su punto de aplicación y las fuerzas individuales tienen puntos de aplicación . Puede ser que no haya ningún punto de aplicación que produzca una resultante sin torque.${\displaystyle \mathbf {F} _ {\mathrm {R} }}$${\displaystyle \mathbf {r}}$${\displaystyle \mathbf {F}_{i}}$${\displaystyle \mathbf {r}_{i}}$

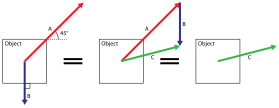
El diagrama opuesto ilustra métodos gráficos simples para encontrar la línea de aplicación de la fuerza resultante de sistemas planos simples:

1. Las líneas de aplicación de las fuerzas reales y en la ilustración más a la izquierda se intersecan. Después de realizar la suma vectorial "en la ubicación de ", la fuerza neta obtenida se traslada de modo que su línea de aplicación pase por el punto de intersección común. Con respecto a ese punto, todos los pares son cero, por lo que el par de la fuerza resultante es igual a la suma de los pares de las fuerzas reales.${\displaystyle \mathbf {F}_{1}}$${\displaystyle \mathbf {F}_{2}}$${\displaystyle \mathbf {F}_{1}}$${\displaystyle \mathbf {F} _ {\mathrm {R} }}$
2. La ilustración en el centro del diagrama muestra dos fuerzas reales paralelas. Después de la suma vectorial "en el punto de ", la fuerza neta se traslada a la línea de aplicación correspondiente, donde se convierte en la fuerza resultante . El procedimiento se basa en la descomposición de todas las fuerzas en componentes para los cuales las líneas de aplicación (líneas de puntos pálidos) se cortan en un punto (el llamado polo, colocado arbitrariamente en el lado derecho de la ilustración). Luego, los argumentos del caso anterior se aplican a las fuerzas y sus componentes para demostrar las relaciones de par.${\displaystyle \mathbf {F}_{2}}$${\displaystyle \mathbf {F} _ {\mathrm {R} }}$
3. La ilustración más a la derecha muestra un par , dos fuerzas iguales pero opuestas para las cuales la cantidad de fuerza neta es cero, pero producen el par neto    donde   es la distancia entre sus líneas de aplicación. Como no hay fuerza resultante, este par puede describirse como par "puro".${\displaystyle \tau = Fd}$${\estilo de visualización \ d}$

En general, un sistema de fuerzas que actúa sobre un cuerpo rígido siempre puede ser reemplazado por una fuerza más un par puro (ver sección anterior). La fuerza es la fuerza neta, pero para calcular el par adicional, a la fuerza neta se le debe asignar la línea de acción. La línea de acción puede seleccionarse arbitrariamente, pero el par puro adicional depende de esta elección. En un caso especial, es posible encontrar una línea de acción tal que este par adicional sea cero.

La fuerza y ​​el par resultantes se pueden determinar para cualquier configuración de fuerzas. Sin embargo, un caso especial interesante es una resultante sin par. Esto es útil, tanto conceptual como prácticamente, porque el cuerpo se mueve sin rotar como si fuera una partícula.

Algunos autores no distinguen la fuerza resultante de la fuerza neta y utilizan los términos como sinónimos . ^[4]

• Teoría del tornillo
• Centro de masa
• Centros de gravedad en campos no uniformes