Modelización matemática de enfermedades infecciosas

Los modelos matemáticos permiten proyectar la evolución de las enfermedades infecciosas para mostrar el posible resultado de una epidemia (incluso en las plantas ) y ayudar a fundamentar las intervenciones en materia de salud pública y fitosanitaria. Los modelos utilizan supuestos básicos o estadísticas recopiladas junto con las matemáticas para encontrar parámetros para diversas enfermedades infecciosas y utilizar esos parámetros para calcular los efectos de diferentes intervenciones, como los programas de vacunación masiva . El modelado puede ayudar a decidir qué intervención(es) evitar y cuál(es) probar, o puede predecir patrones de crecimiento futuros, etc.

La modelización de enfermedades infecciosas es una herramienta que se ha utilizado para estudiar los mecanismos por los cuales se propagan las enfermedades, para predecir el curso futuro de un brote y para evaluar estrategias para controlar una epidemia. ^[1]

El primer científico que intentó cuantificar sistemáticamente las causas de muerte fue John Graunt en su libro Natural and Political Observations made upon the Bills of Mortality , de 1662. Las listas que estudió eran listados de números y causas de muerte que se publicaban semanalmente. El análisis de las causas de muerte de Graunt se considera el comienzo de la "teoría de los riesgos competitivos", que según Daley y Gani ^[1] es "una teoría que ahora está bien establecida entre los epidemiólogos modernos".

El primer modelo matemático de propagación de enfermedades lo realizó Daniel Bernoulli en 1760. Bernoulli, médico de formación, creó un modelo matemático para defender la práctica de la inoculación contra la viruela . ^[2] Los cálculos de este modelo demostraron que la inoculación universal contra la viruela aumentaría la esperanza de vida de 26 años y 7 meses a 29 años y 9 meses. ^[3] El trabajo de Daniel Bernoulli precedió a la comprensión moderna de la teoría de los gérmenes . ^[4]

A principios del siglo XX, William Hamer ^[5] y Ronald Ross ^[6] aplicaron la ley de acción de masas para explicar el comportamiento epidémico.

En la década de 1920 surgieron los modelos compartimentados. El modelo epidémico de Kermack-McKendrick (1927) y el modelo epidémico de Reed-Frost (1928) describen la relación entre individuos susceptibles , infectados e inmunes en una población. El modelo epidémico de Kermack-McKendrick logró predecir el comportamiento de los brotes de manera muy similar a la observada en muchas epidemias registradas. ^[7]

Recientemente, se han utilizado modelos basados ​​en agentes (MBA) en lugar de modelos compartimentados más simples . ^[8] Por ejemplo, los MBA epidemiológicos se han utilizado para informar intervenciones de salud pública (no farmacéuticas) contra la propagación del SARS-CoV-2 . ^[9] Los MBA epidemiológicos, a pesar de su complejidad y de requerir un alto poder computacional, han sido criticados por simplificar y hacer suposiciones poco realistas. ^{[10] [11]} Aun así, pueden ser útiles para informar decisiones sobre medidas de mitigación y supresión en casos en que los MBA estén calibrados con precisión. ^[12]

Los modelos son tan buenos como las hipótesis en las que se basan. Si un modelo hace predicciones que no se ajustan a los resultados observados y las matemáticas son correctas, las hipótesis iniciales deben cambiar para que el modelo sea útil. ^[13]

• Distribución por edad rectangular y estacionaria , es decir, todos los miembros de la población viven hasta la edad L y luego mueren, y para cada edad (hasta L ) hay el mismo número de personas en la población. Esto suele estar bien justificado en los países desarrollados, donde hay una baja mortalidad infantil y gran parte de la población vive hasta la esperanza de vida.
• Mezcla homogénea de la población, es decir, los individuos de la población bajo escrutinio se seleccionan y entran en contacto al azar y no se mezclan principalmente en un subgrupo más pequeño. Esta suposición rara vez se justifica porque la estructura social está muy extendida. Por ejemplo, la mayoría de las personas en Londres solo entran en contacto con otros londinenses. Además, dentro de Londres hay subgrupos más pequeños, como la comunidad turca o los adolescentes (solo para dar dos ejemplos), que se mezclan entre sí más que las personas fuera de su grupo. Sin embargo, la mezcla homogénea es una suposición estándar para que las matemáticas sean manejables.

"Estocástico" significa ser o tener una variable aleatoria. Un modelo estocástico es una herramienta para estimar distribuciones de probabilidad de resultados potenciales al permitir la variación aleatoria en uno o más datos de entrada a lo largo del tiempo. Los modelos estocásticos dependen de las variaciones aleatorias en el riesgo de exposición, enfermedad y otras dinámicas de enfermedades. La diseminación estadística de la enfermedad a nivel de agente en poblaciones pequeñas o grandes se puede determinar mediante métodos estocásticos. ^{[14] [15] [16]}

Cuando se trata de poblaciones grandes, como en el caso de la tuberculosis, se suelen utilizar modelos matemáticos deterministas o compartimentados. En un modelo determinista, los individuos de la población se asignan a diferentes subgrupos o compartimentos, cada uno de los cuales representa una etapa específica de la epidemia. ^[17]

Las tasas de transición de una clase a otra se expresan matemáticamente como derivadas, por lo que el modelo se formula utilizando ecuaciones diferenciales. Al construir estos modelos, se debe suponer que el tamaño de la población en un compartimento es diferenciable con respecto al tiempo y que el proceso epidémico es determinista. En otras palabras, los cambios en la población de un compartimento se pueden calcular utilizando únicamente la historia que se utilizó para desarrollar el modelo. ^[7]

Una explicación habitual del crecimiento de las epidemias es que una persona infecta a dos, esas dos infectan a cuatro, y así sucesivamente, duplicando el número de infectados en cada generación. Es como un juego de la mancha en el que una persona toca a dos, esas dos tocan a otras cuatro que nunca han sido tocadas, y así sucesivamente. A medida que avanza el juego se vuelve cada vez más frenético, ya que los tocados pasan corriendo por delante de los tocados anteriormente para cazar a los que nunca han sido tocados. Así, este modelo de epidemia conduce a una curva que crece exponencialmente hasta que se desploma a cero, ya que toda la población ha sido infectada, es decir, no hay inmunidad de grupo ni pico ni descenso gradual como se ve en la realidad. ^[18]

Las epidemias pueden modelarse como enfermedades que se propagan a través de redes de contacto entre personas. Dicha red puede representarse matemáticamente con un gráfico y se denomina red de contacto. ^[19] Cada nodo de una red de contacto es una representación de un individuo y cada enlace (borde) entre un par de nodos representa el contacto entre ellos. Los enlaces de las redes de contacto pueden usarse para transmitir la enfermedad entre los individuos y cada enfermedad tiene su propia dinámica sobre su red de contacto. La combinación de la dinámica de la enfermedad bajo la influencia de las intervenciones, si las hay, en una red de contacto puede modelarse con otra red, conocida como red de transmisión. En una red de transmisión, todos los enlaces son responsables de transmitir la enfermedad. Si dicha red es una red local similar a un árbol, lo que significa que cualquier vecindario local en dicha red toma la forma de un árbol , entonces la reproducción básica puede escribirse en términos del grado de exceso promedio de la red de transmisión de tal manera que:

$${\displaystyle R_{0}={\frac {\langle k^{2}\rangle }{\langle k\rangle }}-1,}$$

donde es el grado medio (grado promedio) de la red y es el segundo momento de la distribución de grados de la red de transmisión . Sin embargo, no siempre es sencillo encontrar la red de transmisión a partir de la red de contacto y la dinámica de la enfermedad. ^[20] Por ejemplo, si una red de contacto se puede aproximar con un gráfico de Erdős–Rényi con una distribución de grados de Poisson , y los parámetros de propagación de la enfermedad son como se definen en el ejemplo anterior, de modo que es la tasa de transmisión por persona y la enfermedad tiene un período infeccioso medio de , entonces el número básico de reproducción es ^{[21] [22]} ya que para una distribución de Poisson.${\displaystyle {\langle k\rangle }}$${\displaystyle {\langle k^{2}\rangle }}$${\estilo de visualización \beta}$${\displaystyle {\dfrac {1}{\gamma }}}$${\displaystyle R_{0}={\dfrac {\beta }{\gamma }}{\langle k\rangle }}$${\displaystyle {\langle k^{2}\rangle }-{\langle k\rangle }^{2}={\langle k\rangle }}$

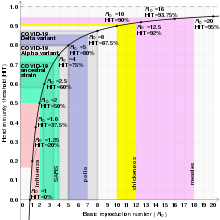
El número básico de reproducción (denotado por R ₀ ) es una medida de cuán transmisible es una enfermedad. Es el número promedio de personas que una sola persona infectada infectará a lo largo de su infección. Esta cantidad determina si la infección aumentará subexponencialmente , se extinguirá o permanecerá constante: si R ₀ > 1, entonces cada persona en promedio infecta a más de otra persona, por lo que la enfermedad se propagará; si R ₀ < 1, entonces cada persona infecta a menos de una persona en promedio, por lo que la enfermedad se extinguirá; y si R ₀ = 1, entonces cada persona infectará en promedio exactamente a otra persona, por lo que la enfermedad se volverá endémica: se propagará por toda la población, pero no aumentará ni disminuirá. ^[23]

Se dice que una enfermedad infecciosa es endémica cuando puede mantenerse en una población sin necesidad de factores externos. Esto significa que, en promedio, cada persona infectada está infectando exactamente a otra persona (si hay más, el número de personas infectadas aumentará de manera subexponencial y habrá una epidemia ; si hay menos, la enfermedad desaparecerá). En términos matemáticos, esto es:

${\displaystyle \ R_{0}S\ = 1.}$

El número básico de reproducción ( R ₀ ) de la enfermedad, suponiendo que todos son susceptibles, multiplicado por la proporción de la población que es realmente susceptible ( S ) debe ser uno (ya que aquellos que no son susceptibles no figuran en nuestros cálculos porque no pueden contraer la enfermedad). Nótese que esta relación significa que para que una enfermedad esté en el estado estable endémico , cuanto mayor sea el número básico de reproducción, menor debe ser la proporción de la población susceptible, y viceversa. Esta expresión tiene limitaciones en cuanto a la proporción de susceptibilidad, por ejemplo, si R ₀ es igual a 0,5, implica que S debe ser 2; sin embargo, esta proporción excede el tamaño de la población. ^{[ cita requerida ]}

Supongamos que la distribución de edad es estacionaria y que las edades de infección tienen la misma distribución para cada año de nacimiento. Sea A la edad promedio de infección , por ejemplo, cuando los individuos menores de A son susceptibles y los mayores de A son inmunes (o infecciosos). Entonces se puede demostrar mediante un argumento fácil que la proporción de la población que es susceptible está dada por:

${\displaystyle S={\frac {A}{L}}.}$

Reiteramos que L es la edad a la que, en este modelo, se supone que muere cada individuo. Pero la definición matemática del estado estacionario endémico se puede reorganizar para dar:

${\displaystyle S={\frac {1}{R_{0}}}.}$

Por lo tanto, debido a la propiedad transitiva :

${\displaystyle {\frac {1}{R_{0}}}={\frac {A}{L}}\Rightarrow R_{0}={\frac {L}{A}}.}$

Esto proporciona una forma sencilla de estimar el parámetro R ₀ utilizando datos fácilmente disponibles.

Para una población con una distribución de edad exponencial ,

${\displaystyle R_{0}=1+{\frac {L}{A}}.}$

Esto permite obtener el número básico de reproducción de una enfermedad dada A y L en cualquier tipo de distribución de población.

Los modelos compartimentales se formulan como cadenas de Markov . ^[24] Un modelo compartimental clásico en epidemiología es el modelo SIR, que puede utilizarse como modelo simple para modelar epidemias. También se emplean muchos otros tipos de modelos compartimentales.

En 1927, WO Kermack y AG McKendrick crearon un modelo en el que consideraron una población fija con solo tres compartimentos: susceptible, ; infectado, ; y recuperado, . Los compartimentos utilizados para este modelo consisten en tres clases: ^[25]${\displaystyle S(t)}$${\displaystyle I(t)}$${\displaystyle R(t)}$

• ${\displaystyle S(t)}$Se utiliza para representar a los individuos que aún no están infectados con la enfermedad en el momento t, o aquellos susceptibles a la enfermedad de la población.
• ${\displaystyle I(t)}$designa a los individuos de la población que han sido infectados con la enfermedad y son capaces de transmitirla a aquellos en la categoría susceptible.
• ${\displaystyle R(t)}$Es el compartimento que se utiliza para los individuos de la población que han sido infectados y luego eliminados de la enfermedad, ya sea por inmunización o por muerte. Los que se encuentran en esta categoría no pueden volver a infectarse ni transmitir la infección a otros.

Existen muchas modificaciones del modelo SIR, incluidas aquellas que incluyen nacimientos y muertes, donde tras la recuperación no hay inmunidad (modelo SIS), donde la inmunidad dura solo un corto período de tiempo (SIRS), donde hay un período latente de la enfermedad donde la persona no es infecciosa ( SEIS y SEIR ), y donde los bebés pueden nacer con inmunidad (MSIR). ^{[ cita requerida ]}

Los modelos matemáticos deben integrar el volumen cada vez mayor de datos que se generan sobre las interacciones entre el huésped y el patógeno . Muchos estudios teóricos sobre la dinámica de las poblaciones , la estructura y la evolución de las enfermedades infecciosas de plantas y animales, incluidos los humanos, se ocupan de este problema. ^[26]

Los temas de investigación incluyen:

• cambio antigénico
• redes epidemiológicas
• evolución y propagación de la resistencia
• inmunoepidemiología​
• dinámica intra-huésped
• Pandemia
• genética de poblaciones de patógenos
• Persistencia de patógenos dentro de los huéspedes
• filodinámica
• Función e identificación de los reservorios de infección
• Papel de los factores genéticos del huésped
• epidemiología espacial
• Herramientas e innovaciones estadísticas y matemáticas
• Estructura e interacciones de la cepa (biología)
• Transmisión , propagación y control de la infección
• virulencia

Si la proporción de la población que es inmune excede el nivel de inmunidad de grupo para la enfermedad, entonces la enfermedad ya no puede persistir en la población y su transmisión se extingue. ^[27] Por lo tanto, una enfermedad puede eliminarse de una población si suficientes individuos son inmunes debido a la vacunación o la recuperación de la exposición previa a la enfermedad. Por ejemplo, la erradicación de la viruela , con el último caso salvaje en 1977, y la certificación de la erradicación de la transmisión autóctona de 2 de los 3 tipos de poliovirus salvajes (tipo 2 en 2015, después del último caso notificado en 1999, y tipo 3 en 2019, después del último caso notificado en 2012). ^[28]

El nivel de inmunidad colectiva se denotará como q . Recordemos que, para un estado estable: ^{[ cita requerida ]}

${\displaystyle R_{0}\cdot S=1.}$

Sucesivamente,

${\displaystyle R_{0}={\frac {N}{S}}={\frac {\mu N\operatorname {E} (T_{L})}{\mu N\operatorname {E} [\min(T_{L},T_{S})]}}={\frac {\operatorname {E} (T_{L})}{\operatorname {E} [\min(T_{L},T_{S})]}},}$

que es aproximadamente: ^{[ cita requerida ]}

${\displaystyle {\frac {\operatorname {\operatorname {E} } (T_{L})}{\operatorname {\operatorname {E} } (T_{S})}}=1+{\frac {\lambda }{\mu }}={\frac {\beta N}{v}}.}$

S será (1 −  q ), ya que q es la proporción de la población que es inmune y q  +  S debe ser igual a uno (ya que en este modelo simplificado, todos son susceptibles o inmunes). Entonces:

${\displaystyle {\begin{aligned}&R_{0}\cdot (1-q)=1,\\[6pt]&1-q={\frac {1}{R_{0}}},\\[6pt]&q=1-{\frac {1}{R_{0}}}.\end{aligned}}}$

Recuerde que este es el nivel umbral. La muerte por transmisión solo ocurrirá si la proporción de individuos inmunes supera este nivel debido a un programa de vacunación masiva.

Acabamos de calcular el umbral crítico de inmunización (denominado q _c ). Es la proporción mínima de la población que debe ser inmunizada al nacer (o cerca del nacimiento) para que la infección desaparezca en la población.

${\displaystyle q_{c}=1-{\frac {1}{R_{0}}}.}$

Porque la fracción del tamaño final de la población p que nunca se infecta se puede definir como:

${\displaystyle \lim _{t\to \infty }S(t)=e^{-\int _{0}^{\infty }\lambda (t)\,dt}=1-p.}$

Por eso,

${\displaystyle p=1-e^{-\int _{0}^{\infty }\beta I(t)\,dt}=1-e^{-R_{0}p}.}$

Resolviendo para , obtenemos:${\displaystyle R_{0}}$

${\displaystyle R_{0}={\frac {-\ln(1-p)}{p}}.}$

Si la vacuna utilizada no es lo suficientemente eficaz o no se puede alcanzar la cobertura requerida, el programa puede no superar el _{límite de vacunación} . Un programa de este tipo protegerá a las personas vacunadas de la enfermedad, pero puede cambiar la dinámica de la transmisión. ^{[ cita requerida ]}

Supongamos que una proporción de la población q (donde q < q _c ) está inmunizada al nacer contra una infección con R ₀  > 1. El programa de vacunación cambia R ₀ a R _q donde

${\displaystyle R_{q}=R_{0}(1-q)}$

Este cambio se produce simplemente porque ahora hay menos personas susceptibles en la población que pueden infectarse. R _q es simplemente R ₀ menos aquellas que normalmente se infectarían pero que ahora no pueden infectarse porque son inmunes.

Como consecuencia de este número básico de reproducción más bajo , la edad promedio de infección A también cambiará a un nuevo valor A _q en aquellos que no hayan sido vacunados.

Recordemos la relación que vinculaba R ₀ , A y L . Suponiendo que la esperanza de vida no ha cambiado, ahora: ^{[ cita requerida ]}

${\displaystyle R_{q}={\frac {L}{A_{q}}},}$

${\displaystyle A_{q}={\frac {L}{R_{q}}}={\frac {L}{R_{0}(1-q)}}.}$

Pero R ₀ = L / A entonces:

${\displaystyle A_{q}={\frac {L}{(L/A)(1-q)}}={\frac {AL}{L(1-q)}}={\frac {A}{1-q}}.}$

Por lo tanto, el programa de vacunación puede aumentar la edad promedio de infección y las personas no vacunadas experimentarán una menor fuerza de infección debido a la presencia del grupo vacunado. En el caso de una enfermedad que conduce a una mayor gravedad clínica en las poblaciones de mayor edad, la proporción de la población no vacunada puede contraer la enfermedad relativamente más tarde en la vida de lo que ocurriría en ausencia de la vacuna.

Si un programa de vacunación hace que la proporción de individuos inmunes en una población supere el umbral crítico durante un período de tiempo significativo, la transmisión de la enfermedad infecciosa en esa población se detendrá. Si la eliminación se produce en todas partes al mismo tiempo, esto puede conducir a la erradicación . ^{[ cita requerida ]}

Eliminación

La interrupción de la transmisión endémica de una enfermedad infecciosa, que ocurre si cada individuo infectado infecta a menos de otro, se logra manteniendo la cobertura de vacunación para mantener la proporción de individuos inmunes por encima del umbral crítico de inmunización. ^{[ cita requerida ]}

Erradicación

Eliminación en todas partes al mismo tiempo, de modo que el agente infeccioso muere (por ejemplo, la viruela y la peste bovina ). ^{[ cita requerida ]}

Los modelos tienen la ventaja de examinar múltiples resultados simultáneamente, en lugar de hacer un único pronóstico. Los modelos han demostrado amplios grados de confiabilidad en pandemias pasadas, como el SARS , el SARS-CoV-2 , ^[29] la gripe porcina , el MERS y el ébola . ^[30]

Software

• Model-Builder: software interactivo (basado en GUI) para construir, simular y analizar modelos ODE.
• Simulador GLEaMviz: permite la simulación de enfermedades infecciosas emergentes que se propagan por todo el mundo.
• STEM: Marco de código abierto para modelado epidemiológico disponible a través de la Fundación Eclipse.
• Paquete R de vigilancia: modelado y monitoreo temporal y espacio-temporal de fenómenos epidémicos