Modelo de Bohr

En física atómica , el modelo de Bohr o modelo de Rutherford-Bohr fue el primer modelo exitoso del átomo . Desarrollado entre 1911 y 1918 por Niels Bohr y basado en el modelo nuclear de Ernest Rutherford , suplantó al modelo de pudín de pasas de JJ Thomson solo para ser reemplazado por el modelo atómico cuántico en la década de 1920. Consiste en un núcleo pequeño y denso rodeado de electrones en órbita . Es análogo a la estructura del Sistema Solar , pero con atracción proporcionada por la fuerza electrostática en lugar de la gravedad , y con las energías de los electrones cuantizadas (asumiendo solo valores discretos).
En la historia de la física atómica, siguió y finalmente reemplazó a varios modelos anteriores, incluido el modelo del sistema solar de Joseph Larmor (1897), el modelo de Jean Perrin (1901), [2] el modelo cúbico (1902), el modelo saturniano de Hantaro Nagaoka (1904), el modelo del pudín de pasas (1904), el modelo cuántico de Arthur Haas (1910), el modelo de Rutherford (1911) y el modelo cuántico nuclear de John William Nicholson (1912). La mejora sobre el modelo de Rutherford de 1911 se refería principalmente a la nueva interpretación mecánica cuántica introducida por Haas y Nicholson, pero abandonando cualquier intento de explicar la radiación según la física clásica .
El éxito clave del modelo radica en explicar la fórmula de Rydberg para las líneas de emisión espectral del hidrógeno . Si bien la fórmula de Rydberg ya se conocía experimentalmente, no obtuvo una base teórica hasta que se introdujo el modelo de Bohr. El modelo de Bohr no solo explicó las razones de la estructura de la fórmula de Rydberg, sino que también proporcionó una justificación para las constantes físicas fundamentales que conforman los resultados empíricos de la fórmula.
El modelo de Bohr es un modelo relativamente primitivo del átomo de hidrógeno , en comparación con el modelo de capa de valencia . Como teoría, se puede derivar como una aproximación de primer orden del átomo de hidrógeno utilizando la mecánica cuántica más amplia y mucho más precisa y, por lo tanto, puede considerarse una teoría científica obsoleta . Sin embargo, debido a su simplicidad y sus resultados correctos para sistemas seleccionados (ver más abajo para la aplicación), el modelo de Bohr todavía se enseña comúnmente para introducir a los estudiantes a la mecánica cuántica o los diagramas de niveles de energía antes de pasar al átomo de capa de valencia más preciso, pero más complejo. Arthur Erich Haas propuso un modelo cuántico relacionado en 1910, pero fue rechazado hasta el Congreso Solvay de 1911, donde se discutió en profundidad. [3] La teoría cuántica del período entre el descubrimiento del cuanto por parte de Planck (1900) y el advenimiento de una mecánica cuántica madura (1925) a menudo se conoce como la antigua teoría cuántica .
Fondo

Hasta la segunda década del siglo XX, los modelos atómicos eran generalmente especulativos. Incluso el concepto de átomos, y más aún el de átomos con estructura interna, se enfrentó a la oposición de algunos científicos. [5] : 2
Modelos planetarios
A finales del siglo XIX, las especulaciones sobre la posible estructura del átomo incluían modelos planetarios con electrones cargados en órbita. [6] : 35 Estos modelos se enfrentaban a una limitación importante. En 1897, Joseph Larmor demostró que una carga acelerada irradiaría potencia según la electrodinámica clásica, un resultado conocido como la fórmula de Larmor . Dado que los electrones obligados a permanecer en órbita están acelerando continuamente, serían mecánicamente inestables. Larmor observó que el efecto electromagnético de múltiples electrones, adecuadamente dispuestos, se cancelarían entre sí. Por lo tanto, los modelos atómicos posteriores basados en la electrodinámica clásica necesitaban adoptar tales disposiciones especiales de múltiples electrones. [7] : 113
Modelo atómico de Thomson
Cuando Bohr comenzó su trabajo en una nueva teoría atómica en el verano de 1912 [8] : 237 el modelo atómico propuesto por JJ Thomson , ahora conocido como el modelo del pudín de pasas , era el mejor disponible. [9] : 37 Thomson propuso un modelo con electrones rotando en anillos coplanares dentro de un volumen esférico de tamaño atómico, cargado positivamente. Thomson demostró que este modelo era mecánicamente estable mediante largos cálculos y era electrodinámicamente estable bajo su suposición original de miles de electrones por átomo. Además, sugirió que las configuraciones particularmente estables de los electrones en anillos estaban conectadas a las propiedades químicas de los átomos. Desarrolló una fórmula para la dispersión de partículas beta que parecía coincidir con los resultados experimentales. [9] : 38 Sin embargo, el propio Thomson demostró más tarde que el átomo tenía un factor de mil electrones menos, desafiando el argumento de la estabilidad y obligando a la esfera positiva poco entendida a tener la mayor parte de la masa del átomo. Thomson tampoco pudo explicar las numerosas líneas en los espectros atómicos. [5] : 18
Modelo nuclear de Rutherford
En 1908, Hans Geiger y Ernest Marsden demostraron que las partículas alfa ocasionalmente se dispersan en ángulos grandes, un resultado inconsistente con el modelo de Thomson. En 1911, Ernest Rutherford desarrolló un nuevo modelo de dispersión, mostrando que la dispersión de ángulo grande observada podría explicarse por una masa compacta y altamente cargada en el centro del átomo. La dispersión de Rutherford no involucraba a los electrones y, por lo tanto, su modelo del átomo estaba incompleto. [10] Bohr comienza su primer artículo sobre su modelo atómico describiendo el átomo de Rutherford como consistente en un núcleo pequeño, denso y con carga positiva que atrae electrones con carga negativa . [11]
Espectros atómicos
A principios del siglo XX, se esperaba que el átomo explicara las muchas líneas espectrales atómicas. Estas líneas fueron resumidas en una fórmula empírica por Johann Balmer y Johannes Rydberg . En 1897, Lord Rayleigh demostró que las vibraciones de los sistemas eléctricos predecían líneas espectrales que dependen del cuadrado de la frecuencia vibratoria, contradiciendo la fórmula empírica que dependía directamente de la frecuencia. [5] : 18 [12] En 1907, Arthur W. Conway demostró que, en lugar de que vibrara todo el átomo, las vibraciones de solo uno de los electrones en el sistema descrito por Thomson podrían ser suficientes para explicar las series espectrales. [13] : II:106 Aunque el modelo de Bohr también se basaría solo en el electrón para explicar el espectro, no asumió un modelo electrodinámico para el átomo.
El otro avance importante en la comprensión de los espectros atómicos fue el principio de combinación de Rydberg-Ritz que relacionaba las frecuencias de las líneas espectrales atómicas con las diferencias entre "términos", frecuencias especiales características de cada elemento. [14] : 173 Bohr reconocería los términos como niveles de energía del átomo divididos por la constante de Planck, lo que llevó a la visión moderna de que las líneas espectrales resultan de diferencias de energía. [15] : 847 [16]
Modelo atómico de Haas
En 1910, Arthur Erich Haas propuso un modelo del átomo de hidrógeno con un electrón circulando sobre la superficie de una esfera de carga positiva. El modelo se parecía al modelo del pudín de pasas de Thomson, pero Haas añadió un giro radical: limitó la energía potencial del electrón, , en una esfera de radio a para que fuera igual a la frecuencia, f , de la órbita del electrón en la esfera multiplicada por la constante de Planck : [14] : 197 donde e representa la carga del electrón y la esfera. Haas combinó esta restricción con la ecuación de equilibrio de fuerzas. La fuerza de atracción entre el electrón y la esfera equilibra la fuerza centrífuga : donde m es la masa del electrón. Esta combinación relaciona el radio de la esfera con la constante de Planck: Haas resolvió la constante de Planck utilizando el valor actual en ese momento para el radio del átomo de hidrógeno. Tres años después, Bohr utilizaría ecuaciones similares con una interpretación diferente. Bohr tomó la constante de Planck como valor dado y utilizó las ecuaciones para predecir, a , el radio del electrón que orbita en el estado fundamental del átomo de hidrógeno. Este valor ahora se llama radio de Bohr . [14] : 197
Influencia de la Conferencia Solvay
La primera Conferencia Solvay , en 1911, fue una de las primeras conferencias internacionales de física. Asistieron nueve premios Nobel o futuros premios Nobel, incluido Ernest Rutherford , el mentor de Bohr. [17] : 271 Bohr no asistió, pero leyó los informes Solvay [18] y los discutió con Rutherford. [8] : 233
El tema de la conferencia fue la teoría de la radiación y los cuantos de energía de los osciladores de Max Planck . [19] La conferencia de Planck en la conferencia terminó con comentarios sobre los átomos y la discusión que la siguió se centró en los modelos atómicos. Hendrik Lorentz planteó la cuestión de la composición del átomo basándose en el modelo de Haas, una forma del modelo del pudín de pasas de Thomson con una modificación cuántica. Lorentz explicó que el tamaño de los átomos podía tomarse para determinar la constante de Planck como lo había hecho Haas o que la constante de Planck podía tomarse como determinante del tamaño de los átomos. [17] : 273 Bohr adoptaría el segundo camino.
Las discusiones subrayaron la necesidad de incluir la teoría cuántica en el átomo. Planck menciona explícitamente las fallas de la mecánica clásica. [17] : 273 Mientras que Bohr ya había expresado una opinión similar en su tesis doctoral, en Solvay los científicos más destacados de la época discutieron una ruptura con las teorías clásicas. [8] : 244 El primer artículo de Bohr sobre su modelo atómico cita las actas de Solvay diciendo: "Cualquiera que sea la alteración en las leyes del movimiento de los electrones, parece necesario introducir en las leyes en cuestión una cantidad ajena a la electrodinámica clásica, es decir , la constante de Planck, o como a menudo se la llama, el cuanto elemental de acción". [11] Alentado por las discusiones de Solvay, Bohr asumiría que el átomo era estable y abandonaría los esfuerzos por estabilizar los modelos clásicos del átomo. [14] : 199
Teoría del átomo de Nicholson
En 1911, John William Nicholson publicó un modelo del átomo que influiría en el modelo de Bohr. Nicholson desarrolló su modelo basándose en el análisis de la espectroscopia astrofísica. Conectó las frecuencias de las líneas espectrales observadas con las órbitas de los electrones en sus átomos. La conexión que adoptó asoció el momento angular orbital del electrón atómico con la constante de Planck . Mientras que Planck se centró en un cuanto de energía, el cuanto de momento angular de Nicholson se relaciona con la frecuencia orbital. Este nuevo concepto dio a la constante de Planck un significado atómico por primera vez. [20] : 169 En su artículo de 1913, Bohr cita a Nicholson por haber encontrado que el momento angular cuantizado es importante para el átomo. [11]
La otra influencia crítica del trabajo de Nicholson fue su análisis detallado de los espectros. Antes del trabajo de Nicholson, Bohr pensaba que los datos espectrales no eran útiles para comprender los átomos. Al comparar su trabajo con el de Nicholson, Bohr llegó a comprender los datos espectrales y su valor. Cuando un amigo le habló de la fórmula compacta de Balmer para los datos de las líneas espectrales, Bohr se dio cuenta rápidamente de que su modelo coincidiría con ella en detalle. [20] : 178
El modelo de Nicholson se basaba en la electrodinámica clásica siguiendo las líneas del modelo del pudín de pasas de JJ Thomson , pero sus electrones negativos orbitaban alrededor de un núcleo positivo en lugar de circular en una esfera. Para evitar el colapso inmediato de este sistema, exigió que los electrones vinieran en pares para que la aceleración rotacional de cada electrón fuera igualada a lo largo de la órbita. [20] : 163 En 1913, Bohr ya había demostrado, a partir del análisis de la pérdida de energía de las partículas alfa, que el hidrógeno tenía solo un electrón, no un par igualado. [14] : 195 El modelo atómico de Bohr abandonaría la electrodinámica clásica.
El modelo de radiación de Nicholson era cuántico, pero estaba vinculado a las órbitas de los electrones. [21] [19] La cuantificación de Bohr lo asociaría con las diferencias en los niveles de energía de su modelo de hidrógeno en lugar de con la frecuencia orbital.
Trabajos previos de Bohr
Bohr completó su doctorado en 1911 con una tesis titulada 'Estudios sobre la teoría electrónica de los metales', una aplicación de la teoría electrónica clásica de Hendrik Lorentz . Bohr observó dos deficiencias del modelo clásico. La primera se refería al calor específico de los metales, que James Clerk Maxwell observó en 1875: cada grado adicional de libertad en una teoría de los metales, como los electrones subatómicos, causa más desacuerdo con la experimentación. La segunda, la teoría clásica no podía explicar el magnetismo. [14] : 194
Después de su doctorado, Bohr trabajó brevemente en el laboratorio de JJ Thomson antes de trasladarse al laboratorio de Rutherford en Manchester para estudiar la radiactividad. Llegó justo después de que Rutherford completara su propuesta de un núcleo nuclear compacto para los átomos. Charles Galton Darwin , también en Manchester, acababa de completar un análisis de la pérdida de energía de las partículas alfa en los metales, concluyendo que las colisiones de electrones eran la causa principal de la pérdida. Bohr demostró en un artículo posterior que los resultados de Darwin mejorarían si se tuviera en cuenta la energía de enlace de los electrones. Es importante destacar que esto le permitió a Bohr concluir que los átomos de hidrógeno tienen un solo electrón. [14] : 195
Desarrollo
Luego, su amigo Hans Hansen le dijo a Bohr que la serie de Balmer se calcula utilizando la fórmula de Balmer, una ecuación empírica descubierta por Johann Balmer en 1885 que describía las longitudes de onda de algunas líneas espectrales del hidrógeno. [18] [22] Johannes Rydberg la generalizó aún más en 1888, dando como resultado lo que ahora se conoce como la fórmula de Rydberg . Después de esto, Bohr declaró que "todo quedó claro". [22]
En 1913, Niels Bohr propuso tres postulados para proporcionar un modelo electrónico coherente con el modelo nuclear de Rutherford:
- El electrón es capaz de girar en determinadas órbitas estables alrededor del núcleo sin irradiar energía, al contrario de lo que sugiere el electromagnetismo clásico . Estas órbitas estables se denominan órbitas estacionarias y se alcanzan a determinadas distancias discretas del núcleo. El electrón no puede tener ninguna otra órbita entre las discretas.
- Las órbitas estacionarias se alcanzan a distancias para las cuales el momento angular del electrón giratorio es un múltiplo entero de la constante de Planck reducida : , donde se llama el número cuántico principal , y . El valor más bajo de es 1; esto da el radio orbital más pequeño posible, conocido como el radio de Bohr , de 0,0529 nm para el hidrógeno. Una vez que un electrón está en esta órbita más baja, no puede acercarse más al núcleo. Partiendo de la regla cuántica del momento angular como Bohr admite que fue dada previamente por Nicholson en su artículo de 1912, [18] [19] [21] [20] Bohr [11] pudo calcular las energías de las órbitas permitidas del átomo de hidrógeno y otros átomos e iones similares al hidrógeno. Estas órbitas están asociadas con energías definidas y también se denominan capas de energía o niveles de energía . En estas órbitas, la aceleración del electrón no da como resultado radiación y pérdida de energía. El modelo de Bohr de un átomo se basó en la teoría cuántica de la radiación de Planck.
- Los electrones sólo pueden ganar y perder energía saltando de una órbita permitida a otra, absorbiendo o emitiendo radiación electromagnética con una frecuencia determinada por la diferencia de energía de los niveles según la relación de Planck : , donde es la constante de Planck.
Otros puntos son:
- Al igual que la teoría del efecto fotoeléctrico de Einstein , la fórmula de Bohr supone que durante un salto cuántico se irradia una cantidad discreta de energía. Sin embargo, a diferencia de Einstein, Bohr se apegó a la teoría clásica de Maxwell del campo electromagnético. La cuantización del campo electromagnético se explicaba por la discreción de los niveles de energía atómica; Bohr no creía en la existencia de fotones . [23] [24]
- Según la teoría de Maxwell, la frecuencia de la radiación clásica es igual a la frecuencia de rotación rot del electrón en su órbita, con armónicos en múltiplos enteros de esta frecuencia. Este resultado se obtiene del modelo de Bohr para saltos entre niveles de energía y cuando es mucho menor que . Estos saltos reproducen la frecuencia del -ésimo armónico de la órbita . Para valores suficientemente grandes de (los llamados estados de Rydberg ), las dos órbitas involucradas en el proceso de emisión tienen casi la misma frecuencia de rotación, de modo que la frecuencia orbital clásica no es ambigua. Pero para valores pequeños (o grandes ), la frecuencia de radiación no tiene una interpretación clásica unívoca. Esto marca el nacimiento del principio de correspondencia , que requiere que la teoría cuántica concuerde con la teoría clásica solo en el límite de números cuánticos grandes.
- La teoría de Bohr-Kramers-Slater (teoría BKS) es un intento fallido de extender el modelo de Bohr, que viola la conservación de la energía y el momento en los saltos cuánticos, y las leyes de conservación solo se cumplen en promedio.
La condición de Bohr, de que el momento angular sea un múltiplo entero de , fue reinterpretada más tarde en 1924 por de Broglie como una condición de onda estacionaria : el electrón se describe mediante una onda y un número entero de longitudes de onda deben caber a lo largo de la circunferencia de la órbita del electrón:
Según la hipótesis de De Broglie, las partículas materiales como el electrón se comportan como ondas . La longitud de onda de De Broglie de un electrón es
Lo que implica que
o
donde es el momento angular del electrón en órbita. Escribiendo para este momento angular, la ecuación anterior se convierte en
que es el segundo postulado de Bohr.
Bohr describió el momento angular de la órbita del electrón como la longitud de onda de De Broglie dividida por el momento del electrón. Sin embargo, en 1913, Bohr justificó su regla apelando al principio de correspondencia, sin proporcionar ningún tipo de interpretación ondulatoria. En 1913, no se sospechaba del comportamiento ondulatorio de partículas materiales como el electrón.
En 1925 se propuso un nuevo tipo de mecánica, la mecánica cuántica , en la que el modelo de Bohr de electrones que se desplazaban en órbitas cuantizadas se amplió para convertirse en un modelo más preciso del movimiento de los electrones. La nueva teoría fue propuesta por Werner Heisenberg . Otra forma de la misma teoría, la mecánica ondulatoria, fue descubierta por el físico austríaco Erwin Schrödinger de forma independiente y mediante un razonamiento diferente. Schrödinger empleó las ondas de materia de De Broglie, pero buscó soluciones ondulatorias de una ecuación de onda tridimensional que describiera electrones que estaban obligados a moverse alrededor del núcleo de un átomo similar al hidrógeno , al quedar atrapados por el potencial de la carga nuclear positiva.
Niveles de energía de los electrones
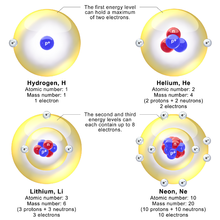
El modelo de Bohr da resultados casi exactos sólo para un sistema donde dos puntos cargados orbitan entre sí a velocidades mucho menores que la de la luz. Esto no sólo involucra sistemas de un electrón como el átomo de hidrógeno , helio de ion simple y litio de ion doble , sino que incluye estados de positronio y Rydberg de cualquier átomo donde un electrón está lejos de todo lo demás. Puede usarse para cálculos de transición de rayos X de línea K si se agregan otras suposiciones (ver la ley de Moseley a continuación). En física de alta energía, puede usarse para calcular las masas de mesones de quarks pesados .
El cálculo de las órbitas requiere dos suposiciones.
- Mecánica clásica
- El electrón se mantiene en una órbita circular por atracción electrostática. La fuerza centrípeta es igual a la fuerza de Coulomb .
- donde m e es la masa del electrón, e es la carga elemental , k e es la constante de Coulomb y Z es el número atómico del átomo . Se supone aquí que la masa del núcleo es mucho mayor que la masa del electrón (lo cual es una buena suposición). Esta ecuación determina la velocidad del electrón en cualquier radio:
- También determina la energía total del electrón en cualquier radio:
- La energía total es negativa e inversamente proporcional a r . Esto significa que se necesita energía para alejar al electrón en órbita del protón. Para valores infinitos de r , la energía es cero, lo que corresponde a un electrón inmóvil infinitamente lejos del protón. La energía total es la mitad de la energía potencial , siendo la diferencia la energía cinética del electrón. Esto también es cierto para órbitas no circulares según el teorema del virial .
- Una regla cuántica
- El momento angular L = m e vr es un múltiplo entero de ħ :
Derivación
En mecánica clásica, si un electrón está orbitando alrededor de un átomo con período T, y si su acoplamiento al campo electromagnético es débil, de modo que la órbita no se desintegra mucho en un ciclo, emitirá radiación electromagnética en un patrón que se repite en cada período, de modo que la transformada de Fourier del patrón solo tendrá frecuencias que sean múltiplos de 1/T.
Sin embargo, en mecánica cuántica, la cuantificación del momento angular conduce a niveles de energía discretos de las órbitas, y las frecuencias emitidas se cuantifican de acuerdo con las diferencias de energía entre estos niveles. Esta naturaleza discreta de los niveles de energía introduce una desviación fundamental de la ley de radiación clásica, dando lugar a líneas espectrales diferenciadas en la radiación emitida.
Bohr supone que el electrón gira alrededor del núcleo en una órbita elíptica obedeciendo las reglas de la mecánica clásica, pero sin pérdida de radiación debido a la fórmula de Larmor .
Denotando la energía total como E , la carga negativa del electrón como e , la carga positiva del núcleo como K=Z|e| , la masa del electrón como m e , la mitad del eje mayor de la elipse como a , comienza con estas ecuaciones: [11] : 3
Se supone que E es negativo, porque se requiere una energía positiva para separar el electrón del núcleo y ponerlo en reposo a una distancia infinita.
La ecuación (1a) se obtiene al igualar la fuerza centrípeta a la fuerza de Coulomb que actúa entre el núcleo y el electrón, considerando que (donde T es la energía cinética promedio y U el potencial electrostático promedio), y que para la segunda ley de Kepler, la separación promedio entre el electrón y el núcleo es a .
La ecuación (1b) se obtiene a partir de las mismas premisas de la ecuación (1a) más el teorema virial , que establece que, para una órbita elíptica,
Entonces Bohr supone que es un múltiplo entero de la energía de un cuanto de luz con la mitad de la frecuencia de revolución del electrón, [11] : 4 es decir:
De la ecuación (1a,1b,2), se desciende:
Además supone que la órbita es circular, es decir , y, denotando el momento angular del electrón como L , introduce la ecuación:
La ecuación (4) se deriva del teorema virial y de las relaciones de la mecánica clásica entre el momento angular, la energía cinética y la frecuencia de revolución.
De la ecuación (1c,2,4), se deduce:
dónde:
eso es:
Este resultado indica que el momento angular del electrón es un múltiplo entero de la constante de Planck reducida. [11] : 15
Sustituyendo la expresión de la velocidad se obtiene una ecuación para r en términos de n :
de modo que el radio de órbita permitido en cualquier n es
El valor más pequeño posible de r en el átomo de hidrógeno ( Z = 1 ) se llama radio de Bohr y es igual a:
La energía del nivel n -ésimo de cualquier átomo está determinada por el radio y el número cuántico:
Por lo tanto, un electrón en el nivel de energía más bajo del hidrógeno ( n = 1 ) tiene aproximadamente 13,6 eV menos energía que un electrón inmóvil infinitamente lejos del núcleo. El siguiente nivel de energía ( n = 2 ) es −3,4 eV. El tercero ( n = 3) es −1,51 eV, y así sucesivamente. Para valores mayores de n , estas también son las energías de enlace de un átomo altamente excitado con un electrón en una gran órbita circular alrededor del resto del átomo. La fórmula del hidrógeno también coincide con el producto de Wallis . [25]
La combinación de constantes naturales en la fórmula energética se denomina energía de Rydberg ( R E ):
Esta expresión se aclara interpretándola en combinaciones que forman unidades más naturales :
- es la energía de masa en reposo del electrón (511 keV),
- es la constante de estructura fina ,
- .
Como esta derivación se basa en el supuesto de que el núcleo está orbitado por un electrón, podemos generalizar este resultado al dejar que el núcleo tenga una carga q = Ze , donde Z es el número atómico. Esto nos dará ahora los niveles de energía para átomos hidrogénicos (similares al hidrógeno), que pueden servir como una aproximación aproximada del orden de magnitud de los niveles de energía reales. Por lo tanto, para los núcleos con Z protones, los niveles de energía son (aproximadamente):
Los niveles de energía reales no se pueden resolver analíticamente para más de un electrón (ver problema de n cuerpos ) porque los electrones no solo se ven afectados por el núcleo sino que también interactúan entre sí a través de la fuerza de Coulomb .
Cuando Z = 1/ α ( Z ≈ 137 ), el movimiento se vuelve altamente relativista y Z 2 cancela el α 2 en R ; la energía de la órbita comienza a ser comparable a la energía en reposo. Los núcleos suficientemente grandes, si fueran estables, reducirían su carga creando un electrón ligado desde el vacío, expulsando el positrón al infinito. Este es el fenómeno teórico del apantallamiento de carga electromagnética que predice una carga nuclear máxima. La emisión de tales positrones se ha observado en las colisiones de iones pesados para crear núcleos superpesados temporales. [26]
La fórmula de Bohr utiliza correctamente la masa reducida del electrón y del protón en todas las situaciones, en lugar de la masa del electrón,
Sin embargo, estos números son casi iguales, debido a la masa mucho mayor del protón, aproximadamente 1836,1 veces la masa del electrón, de modo que la masa reducida en el sistema es la masa del electrón multiplicada por la constante 1836,1/(1+1836,1) = 0,99946. Este hecho fue históricamente importante para convencer a Rutherford de la importancia del modelo de Bohr, ya que explicaba el hecho de que las frecuencias de las líneas en los espectros para el helio individualmente ionizado no difieren de las del hidrógeno en un factor de exactamente 4, sino más bien en 4 veces la relación de la masa reducida para los sistemas de hidrógeno frente a helio, que era mucho más cercana a la relación experimental que exactamente 4.
En el caso del positronio, la fórmula también utiliza la masa reducida, pero en este caso es exactamente la masa del electrón dividida por 2. Para cualquier valor del radio, el electrón y el positrón se mueven cada uno a la mitad de la velocidad alrededor de su centro de masa común, y cada uno tiene solo una cuarta parte de la energía cinética. La energía cinética total es la mitad de lo que sería para un solo electrón moviéndose alrededor de un núcleo pesado.
- (positronio).
Fórmula de Rydberg
A finales de la década de 1860, Johann Balmer y, posteriormente , Johannes Rydberg y Walther Ritz desarrollaron fórmulas empíricas cada vez más precisas que coincidían con las líneas espectrales atómicas medidas. Rydberg expresó su fórmula en términos de número de onda, equivalente a la frecuencia, que fue fundamental para el trabajo posterior de Bohr. [27] Estas fórmulas contenían una constante, , ahora conocida como la constante de Rydberg , y un par de números enteros que indexaban las líneas: [14] : 247 A pesar de muchos intentos, ninguna teoría del átomo pudo reproducir estas fórmulas relativamente simples. [14] : 169
En la teoría de Bohr, la descripción de las energías de transición o saltos cuánticos entre niveles de energía orbital permite explicar estas fórmulas. Para el átomo de hidrógeno, Bohr comienza con su fórmula derivada para la energía liberada cuando un electrón libre se mueve hacia una órbita circular estable indexada por : [28] La diferencia de energía entre dos de estos niveles es entonces: Por lo tanto, la teoría de Bohr proporciona la fórmula de Rydberg y, además, el valor numérico de la constante de Rydberg para el hidrógeno en términos de constantes más fundamentales de la naturaleza, incluida la carga del electrón, la masa del electrón y la constante de Planck : [29] : 31 [30]
Dado que la energía de un fotón es
Estos resultados pueden expresarse en términos de la longitud de onda del fotón emitido:
La derivación de la constante de Rydberg por parte de Bohr, así como la concordancia concomitante de la fórmula de Bohr con las líneas espectrales observadas experimentalmente de las series de Lyman ( n f = 1), Balmer ( n f = 2) y Paschen ( n f = 3), y la predicción teórica exitosa de otras líneas aún no observadas, fue una de las razones por las que su modelo fue aceptado inmediatamente. [30] : 34
Para aplicarla a átomos con más de un electrón, la fórmula de Rydberg se puede modificar reemplazando Z por Z − b o n por n − b, donde b es una constante que representa un efecto de apantallamiento debido a la capa interna y a otros electrones (véase Capa electrónica y el análisis posterior del "modelo de capas del átomo" más abajo). Esto se estableció empíricamente antes de que Bohr presentara su modelo.
Modelo de capas (átomos más pesados)
Los tres artículos originales de Bohr de 1913 describían principalmente la configuración electrónica de los elementos más ligeros. Bohr llamó a sus capas de electrones "anillos" en 1913. Los orbitales atómicos dentro de las capas no existían en la época de su modelo planetario. Bohr explica en la Parte 3 de su famoso artículo de 1913 que el máximo de electrones en una capa es ocho, escribiendo: "Vemos, además, que un anillo de n electrones no puede girar en un solo anillo alrededor de un núcleo de carga n e a menos que n < 8". Para átomos más pequeños, las capas de electrones se llenarían de la siguiente manera: "los anillos de electrones solo se unirán si contienen el mismo número de electrones; y que, en consecuencia, el número de electrones en los anillos internos solo será 2, 4, 8". Sin embargo, en átomos más grandes, la capa más interna contendría ocho electrones, "por otro lado, el sistema periódico de los elementos sugiere firmemente que ya en el neón N = 10 se producirá un anillo interno de ocho electrones". Bohr escribió: "De lo anterior llegamos al siguiente esquema posible para la disposición de los electrones en átomos ligeros:" [31] [4] [8]
| Elemento | Electrones por capa | Elemento | Electrones por capa | Elemento | Electrones por capa |
|---|---|---|---|---|---|
| 1 | 1 | 9 | 4, 4, 1 | 17 | 8, 4, 4, 1 |
| 2 | 2 | 10 | 8, 2 | 18 | 8, 8, 2 |
| 3 | 2, 1 | 11 | 8, 2, 1 | 19 | 8, 8, 2, 1 |
| 4 | 2, 2 | 12 | 8, 2, 2 | 20 | 8, 8, 2, 2 |
| 5 | 2, 3 | 13 | 8, 2, 3 | 21 | 8, 8, 2, 3 |
| 6 | 2, 4 | 14 | 8, 2, 4 | 22 | 8, 8, 2, 4 |
| 7 | 4, 3 | 15 | 8, 4, 3 | 23 | 8, 8, 4, 3 |
| 8 | 4, 2, 2 | 16 | 8, 4, 2, 2 | 24 | 8, 8, 4, 2, 2 |
En la tercera parte del artículo de Bohr de 1913, titulada "Sistemas que contienen varios núcleos", dice que dos átomos forman moléculas en un plano simétrico y vuelve a describir el hidrógeno. [32] El modelo de Bohr de 1913 no analizaba los elementos superiores en detalle y John William Nicholson fue uno de los primeros en demostrar en 1914 que no podía funcionar para el litio, pero era una teoría atractiva para el hidrógeno y el helio ionizado. [8] [33]
En 1921, siguiendo el trabajo de los químicos y otros involucrados en el trabajo sobre la tabla periódica , Bohr amplió el modelo del hidrógeno para dar un modelo aproximado para átomos más pesados. Esto dio una imagen física que reproducía muchas propiedades atómicas conocidas por primera vez, aunque estas propiedades fueron propuestas contemporáneamente con el trabajo idéntico del químico Charles Rugeley Bury [4] [34]
El socio de Bohr en la investigación durante 1914 a 1916 fue Walther Kossel , quien corrigió el trabajo de Bohr para mostrar que los electrones interactuaban a través de los anillos externos, y Kossel llamó a los anillos: "capas". [35] [36] A Irving Langmuir se le atribuye la primera disposición viable de electrones en capas con solo dos en la primera capa y hasta ocho en la siguiente según la regla del octeto de 1904, aunque Kossel ya había predicho un máximo de ocho por capa en 1916. [37] Los átomos más pesados tienen más protones en el núcleo y más electrones para cancelar la carga. Bohr tomó de estos químicos la idea de que cada órbita discreta solo podía contener una cierta cantidad de electrones. Según Kossel , después de que la órbita esté llena, se tendría que utilizar el siguiente nivel. [4] Esto le da al átomo una estructura de capas diseñada por Kossel, Langmuir y Bury, en la que cada capa corresponde a una órbita de Bohr.
Este modelo es incluso más aproximado que el modelo del hidrógeno, porque trata a los electrones de cada capa como si no interactuaran. Pero las repulsiones de los electrones se tienen en cuenta en cierta medida mediante el fenómeno del apantallamiento . Los electrones en órbitas externas no solo orbitan alrededor del núcleo, sino que también se mueven alrededor de los electrones internos, por lo que la carga efectiva Z que sienten se reduce por el número de electrones en la órbita interna.
Por ejemplo, el átomo de litio tiene dos electrones en la órbita 1s más baja, y estos orbitan en Z = 2. Cada uno ve la carga nuclear de Z = 3 menos el efecto de apantallamiento del otro, lo que reduce crudamente la carga nuclear en 1 unidad. Esto significa que los electrones más internos orbitan aproximadamente a la mitad del radio de Bohr. El electrón más externo en el litio orbita aproximadamente a la mitad del radio de Bohr, ya que los dos electrones internos reducen la carga nuclear en 2. Este electrón externo debería estar a casi un radio de Bohr del núcleo. Debido a que los electrones se repelen fuertemente entre sí, la descripción de la carga efectiva es muy aproximada; la carga efectiva Z no suele resultar ser un número entero.
El modelo de capas fue capaz de explicar cualitativamente muchas de las misteriosas propiedades de los átomos que se codificaron a finales del siglo XIX en la tabla periódica de los elementos . Una propiedad era el tamaño de los átomos, que podía determinarse aproximadamente midiendo la viscosidad de los gases y la densidad de los sólidos cristalinos puros. Los átomos tienden a hacerse más pequeños hacia la derecha en la tabla periódica, y se vuelven mucho más grandes en la siguiente línea de la tabla. Los átomos a la derecha de la tabla tienden a ganar electrones, mientras que los átomos a la izquierda tienden a perderlos. Cada elemento en la última columna de la tabla es químicamente inerte ( gas noble ).
En el modelo de capas, este fenómeno se explica por el llenado de capas. Los átomos sucesivos se hacen más pequeños porque están llenando órbitas del mismo tamaño, hasta que la órbita está llena, momento en el que el siguiente átomo en la tabla tiene un electrón externo débilmente unido, lo que hace que se expanda. La primera órbita de Bohr se llena cuando tiene dos electrones, lo que explica por qué el helio es inerte. La segunda órbita permite ocho electrones, y cuando está llena el átomo es neón, nuevamente inerte. El tercer orbital contiene ocho electrones nuevamente, excepto que en el tratamiento más correcto de Sommerfeld (reproducido en la mecánica cuántica moderna) hay electrones "d" adicionales. La tercera órbita puede contener 10 electrones d adicionales, pero estas posiciones no se llenan hasta que se llenan unos pocos orbitales más del siguiente nivel (llenar los orbitales d n = 3 produce los 10 elementos de transición ). El patrón de llenado irregular es un efecto de las interacciones entre electrones, que no se tienen en cuenta ni en los modelos de Bohr ni en los de Sommerfeld y que son difíciles de calcular incluso en el tratamiento moderno.
Ley de Moseley y cálculo (líneas de emisión de rayos X K-alfa)
Niels Bohr dijo en 1962: "En realidad, el trabajo de Rutherford no se tomó en serio. Hoy no lo podemos entender, pero no se lo tomó en serio en absoluto. No se lo mencionó en ningún lugar. El gran cambio vino de Moseley". [38]
En 1913, Henry Moseley encontró una relación empírica entre la línea de rayos X más fuerte emitida por átomos bajo bombardeo de electrones (entonces conocida como la línea K-alfa ), y su número atómico Z. Se encontró que la fórmula empírica de Moseley era derivable de la fórmula de Rydberg y más tarde de la fórmula de Bohr (Moseley en realidad menciona solo a Ernest Rutherford y Antonius Van den Broek en términos de modelos, ya que estos habían sido publicados antes del trabajo de Moseley y el artículo de Moseley de 1913 se publicó el mismo mes que el primer artículo del modelo de Bohr). [39] Las dos suposiciones adicionales de que [1] esta línea de rayos X provenía de una transición entre niveles de energía con números cuánticos 1 y 2, y [2] , que el número atómico Z cuando se usa en la fórmula para átomos más pesados que el hidrógeno, debería disminuirse en 1, a ( Z − 1) 2 .
Moseley le escribió a Bohr, desconcertado por sus resultados, pero Bohr no pudo ayudarlo. En ese momento, pensaba que la capa de electrones "K" más interna postulada debería tener al menos cuatro electrones, no los dos que habrían explicado claramente el resultado. Por lo tanto, Moseley publicó sus resultados sin una explicación teórica.
En 1914 y 1916, Walther Kossel explicó que en la tabla periódica se crearían nuevos elementos a medida que se añadieran electrones a la capa exterior. En su artículo, Kossel escribe: "Esto lleva a la conclusión de que los electrones que se añaden deben colocarse en anillos o capas concéntricos, en cada uno de los cuales... sólo debe disponerse un cierto número de electrones, es decir, ocho en nuestro caso. Tan pronto como se completa un anillo o capa, debe comenzarse uno nuevo para el siguiente elemento; el número de electrones, que son más fácilmente accesibles y se encuentran en la periferia más externa, aumenta de nuevo de un elemento a otro y, por lo tanto, en la formación de cada nueva capa se repite la periodicidad química". [35] [36] Más tarde, el químico Langmuir se dio cuenta de que el efecto se debía a un apantallamiento de carga, con una capa interior que contenía sólo 2 electrones. En su artículo de 1919, Irving Langmuir postuló la existencia de "células" que sólo podían contener dos electrones cada una y que estaban dispuestas en "capas equidistantes".
En el experimento de Moseley, uno de los electrones más internos del átomo es eliminado, dejando una vacante en la órbita de Bohr más baja, que contiene un solo electrón restante. Esta vacante es entonces ocupada por un electrón de la siguiente órbita, que tiene n=2. Pero los electrones n=2 ven una carga efectiva de Z − 1, que es el valor apropiado para la carga del núcleo, cuando un solo electrón permanece en la órbita de Bohr más baja para apantallar la carga nuclear + Z y reducirla en −1 (debido a que la carga negativa del electrón apantalla la carga positiva nuclear). La energía ganada por un electrón que cae de la segunda capa a la primera da la ley de Moseley para las líneas K-alfa,
o
Aquí, R v = R E / h es la constante de Rydberg, en términos de frecuencia igual a 3,28 x 10 15 Hz. Para valores de Z entre 11 y 31, esta última relación había sido derivada empíricamente por Moseley, en un gráfico simple (lineal) de la raíz cuadrada de la frecuencia de rayos X contra el número atómico (sin embargo, para la plata, Z = 47, el término de detección obtenido experimentalmente debería reemplazarse por 0,4). A pesar de su validez restringida, [40] la ley de Moseley no solo estableció el significado objetivo del número atómico, sino que, como señaló Bohr, también hizo más que la derivación de Rydberg para establecer la validez del modelo nuclear de Rutherford/Van den Broek/Bohr del átomo, con el número atómico (lugar en la tabla periódica) representando unidades enteras de carga nuclear. Van den Broek había publicado su modelo en enero de 1913 mostrando que la tabla periódica estaba organizada según la carga, mientras que el modelo atómico de Bohr no se publicó hasta julio de 1913. [41]
Ahora se sabe que la línea K-alfa de la época de Moseley es un par de líneas cercanas, escritas como ( Kα 1 y Kα 2 ) en notación Siegbahn .
Defectos
El modelo de Bohr da un valor incorrecto L = ħ para el momento angular orbital del estado fundamental: se sabe experimentalmente que el momento angular en el estado fundamental verdadero es cero. Aunque las imágenes mentales fallan un poco en estos niveles de escala, se puede pensar que un electrón en el "orbital" moderno más bajo sin momento orbital no gira "alrededor" del núcleo en absoluto, sino que simplemente lo rodea estrechamente en una elipse con área cero (esto se puede imaginar como "de ida y vuelta", sin chocar ni interactuar con el núcleo). Esto solo se reproduce en un tratamiento semiclásico más sofisticado como el de Sommerfeld. Aún así, incluso el modelo semiclásico más sofisticado no logra explicar el hecho de que el estado de energía más bajo es esféricamente simétrico: no apunta en ninguna dirección en particular.
Sin embargo, en el tratamiento cuántico completo moderno en el espacio de fases , la deformación adecuada (extensión completa cuidadosa) del resultado semiclásico ajusta el valor del momento angular al efectivo correcto. [42] Como consecuencia, la expresión del estado fundamental físico se obtiene a través de un desplazamiento de la expresión del momento angular cuántico que se desvanece, que corresponde a la simetría esférica.
En la mecánica cuántica moderna, el electrón del hidrógeno es una nube esférica de probabilidad que se hace más densa cerca del núcleo. La constante de velocidad de decaimiento de la probabilidad en el hidrógeno es igual a la inversa del radio de Bohr, pero como Bohr trabajaba con órbitas circulares, no con elipses de área cero, el hecho de que estos dos números coincidan exactamente se considera una "coincidencia". (Sin embargo, se encuentran muchas coincidencias de este tipo entre el tratamiento semiclásico y el tratamiento mecánico cuántico completo del átomo; estas incluyen niveles de energía idénticos en el átomo de hidrógeno y la derivación de una constante de estructura fina, que surge del modelo relativista de Bohr-Sommerfeld (ver más abajo) y que resulta ser igual a un concepto completamente diferente, en la mecánica cuántica moderna completa).
El modelo de Bohr también tiene dificultades para explicar, o bien no logra hacerlo:
- Gran parte de los espectros de átomos más grandes. En el mejor de los casos, puede hacer predicciones sobre los espectros de emisión de rayos X K-alfa y algunos L-alfa para átomos más grandes, si se hacen dos suposiciones ad hoc adicionales. Los espectros de emisión para átomos con un solo electrón en la capa externa (átomos en el grupo del litio ) también se pueden predecir de manera aproximada. Además, si se conocen los factores de apantallamiento electrón-nuclear empíricos para muchos átomos, se pueden deducir muchas otras líneas espectrales a partir de la información, en átomos similares de diferentes elementos, a través de los principios de combinación de Ritz-Rydberg (ver fórmula de Rydberg ). Todas estas técnicas hacen uso esencialmente de la imagen de energía-potencial newtoniana de Bohr del átomo.
- Las intensidades relativas de las líneas espectrales; aunque en algunos casos simples, la fórmula de Bohr o modificaciones de la misma, fueron capaces de proporcionar estimaciones razonables (por ejemplo, los cálculos de Kramers para el efecto Stark ).
- La existencia de estructura fina y estructura hiperfina en líneas espectrales, que se sabe que se deben a una variedad de efectos relativistas y sutiles, así como a complicaciones del espín del electrón.
- El efecto Zeeman : cambios en las líneas espectrales debidos a campos magnéticos externos ; estos también se deben a principios cuánticos más complicados que interactúan con el espín del electrón y los campos magnéticos orbitales.
- El modelo también viola el principio de incertidumbre porque considera que los electrones tienen órbitas y ubicaciones conocidas, dos cosas que no se pueden medir simultáneamente.
- Los dobletes y tripletes aparecen en los espectros de algunos átomos como pares de líneas muy próximos entre sí. El modelo de Bohr no puede explicar por qué algunos niveles de energía deberían estar muy próximos entre sí.
- Los átomos con múltiples electrones no tienen los niveles de energía previstos por el modelo. No funciona con el helio (neutro).
Refinamientos

Se propusieron varias mejoras al modelo de Bohr, en particular los modelos Sommerfeld o Bohr–Sommerfeld , que sugerían que los electrones viajan en órbitas elípticas alrededor de un núcleo en lugar de las órbitas circulares del modelo de Bohr. [1] Este modelo complementó la condición de momento angular cuantificado del modelo de Bohr con una condición de cuantificación radial adicional, la condición de cuantificación de Wilson – Sommerfeld [43] [44]
donde p r es el momento radial canónicamente conjugado a la coordenada q r , que es la posición radial, y T es un periodo orbital completo. La integral es la acción de las coordenadas del ángulo de acción . Esta condición, sugerida por el principio de correspondencia , es la única posible, ya que los números cuánticos son invariantes adiabáticos .
El modelo de Bohr-Sommerfeld era fundamentalmente inconsistente y conducía a muchas paradojas. El número cuántico magnético medía la inclinación del plano orbital con respecto al plano xy , y solo podía tomar unos pocos valores discretos. Esto contradecía el hecho obvio de que un átomo podía tener cualquier orientación con respecto a las coordenadas, sin restricción. La cuantificación de Sommerfeld se puede realizar en diferentes coordenadas canónicas y, a veces, da diferentes respuestas. La incorporación de correcciones de radiación era difícil, porque requería encontrar coordenadas de ángulo de acción para un sistema combinado radiación/átomo, lo cual es difícil cuando se permite que la radiación escape. La teoría completa no se extendía a los movimientos no integrables, lo que significaba que muchos sistemas no podían ser tratados ni siquiera en principio. Al final, el modelo fue reemplazado por el tratamiento mecánico-cuántico moderno del átomo de hidrógeno , que fue dado por primera vez por Wolfgang Pauli en 1925, utilizando la mecánica matricial de Heisenberg . La imagen actual del átomo de hidrógeno se basa en los orbitales atómicos de la mecánica ondulatoria , que Erwin Schrödinger desarrolló en 1926.
Sin embargo, esto no quiere decir que el modelo de Bohr-Sommerfeld no tuviera éxitos. Los cálculos basados en el modelo de Bohr-Sommerfeld pudieron explicar con precisión una serie de efectos espectrales atómicos más complejos. Por ejemplo, hasta perturbaciones de primer orden , el modelo de Bohr y la mecánica cuántica hacen las mismas predicciones para la división de la línea espectral en el efecto Stark . Sin embargo, en perturbaciones de orden superior, el modelo de Bohr y la mecánica cuántica difieren, y las mediciones del efecto Stark bajo altas intensidades de campo ayudaron a confirmar la exactitud de la mecánica cuántica sobre el modelo de Bohr. La teoría predominante detrás de esta diferencia radica en las formas de los orbitales de los electrones, que varían según el estado de energía del electrón.
Las condiciones de cuantificación de Bohr-Sommerfeld plantean interrogantes en el campo de las matemáticas modernas. La condición de cuantificación semiclásica consistente requiere un cierto tipo de estructura en el espacio de fases, lo que impone limitaciones topológicas a los tipos de variedades simplécticas que se pueden cuantificar. En particular, la forma simpléctica debería ser la forma de curvatura de una conexión de un fibrado lineal hermítico , lo que se denomina precuantificación .
Bohr también actualizó su modelo en 1922, asumiendo que ciertos números de electrones (por ejemplo, 2, 8 y 18) corresponden a " capas cerradas " estables. [45]
Modelo del enlace químico
Niels Bohr propuso un modelo del átomo y un modelo del enlace químico . Según su modelo de molécula diatómica , los electrones de los átomos de la molécula forman un anillo giratorio cuyo plano es perpendicular al eje de la molécula y equidistante de los núcleos atómicos. El equilibrio dinámico del sistema molecular se logra mediante el equilibrio de fuerzas entre las fuerzas de atracción de los núcleos hacia el plano del anillo de electrones y las fuerzas de repulsión mutua de los núcleos. El modelo de Bohr del enlace químico tuvo en cuenta la repulsión de Coulomb : los electrones en el anillo están a la distancia máxima entre sí. [46] [47]
Simbolismo de los modelos atómicos planetarios

Aunque el modelo atómico de Bohr fue reemplazado por los modelos cuánticos en la década de 1920, la imagen visual de los electrones orbitando alrededor de un núcleo ha seguido siendo el concepto popular de átomos. El concepto de átomo como un pequeño sistema planetario se ha utilizado ampliamente como símbolo de los átomos e incluso de la energía "atómica" (aunque se la considera más propiamente energía nuclear). [48] : 58 Algunos ejemplos de su uso durante el siglo pasado incluyen, entre otros:
- El logotipo de la Comisión de Energía Atómica de los Estados Unidos , que fue en parte responsable de su uso posterior en relación con la tecnología de fisión nuclear en particular.
- La bandera del Organismo Internacional de Energía Atómica es un "emblema con un escudo y un átomo girando", [49] rodeado de ramas de olivo .
- El logotipo de Albuquerque Isotopes , una liga menor de béisbol de Estados Unidos , muestra pelotas de béisbol como electrones que orbitan alrededor de una gran letra "A".
- Un símbolo similar, el remolino atómico , fue elegido como símbolo de los ateos estadounidenses y llegó a utilizarse como símbolo del ateísmo en general.
- El punto de código U+269B (⚛) de Símbolos Varios Unicode para un átomo parece un modelo de átomo planetario.
- El programa de televisión The Big Bang Theory utiliza una imagen similar a un planeta en su logotipo impreso.
- La biblioteca de JavaScript React utiliza una imagen similar a un planeta como su logotipo.
- En los mapas, generalmente se utiliza para indicar una instalación de energía nuclear .
Véase también
- 1913 en la ciencia
- La constante de Balmer
- Modelo de Bohr-Sommerfeld
- El experimento de Franck-Hertz proporcionó un apoyo temprano al modelo de Bohr.
- El efecto del par inerte se explica adecuadamente mediante el modelo de Bohr.
- Introducción a la mecánica cuántica
Referencias
Notas al pie
- ^ ab Lakhtakia, Akhlesh; Salpeter, Edwin E. (1996). "Modelos y modeladores del hidrógeno". American Journal of Physics . 65 (9): 933. Bibcode :1997AmJPh..65..933L. doi :10.1119/1.18691.
- ^ Perrin, Jean (1901). "Les Hypothèses moléculaires". La Revue científica : 463.
- ^ de Broglie y col. 1912, págs. 122-123.
- ^ abcd Kragh, Helge (1 de enero de 1979). "La segunda teoría atómica de Niels Bohr". Estudios Históricos en las Ciencias Físicas . 10 : 123–186. doi :10.2307/27757389. JSTOR 27757389.
- ^ abc Kragh, Helge (2012). Niels Bohr y el átomo cuántico: el modelo de Bohr de la estructura atómica 1913-1925 . Oxford University Press. ISBN 978-0-19-163046-0.
- ^ Helge Kragh (octubre de 2010). Antes de Bohr: teorías de la estructura atómica 1850-1913. RePoSS: Publicaciones de investigación sobre estudios científicos 10. Aarhus: Centro de estudios científicos, Universidad de Aarhus.
- ^ Wheaton, Bruce R. (1992). El tigre y el tiburón: raíces empíricas del dualismo onda-partícula (1.ª edición de bolsillo, edición reimpresa). Cambridge: Cambridge Univ. Press. ISBN 978-0-521-35892-7.
- ^ abcde Heilbron, John L.; Kuhn, Thomas S. (1969). "La génesis del átomo de Bohr". Estudios históricos en las ciencias físicas . 1 : vi–290. doi :10.2307/27757291. JSTOR 27757291.
- ^ ab John L, Heilbron (1985). "Las primeras teorías del átomo de Bohr". En francés, AP; Kennedy, PJ (eds.). Niels Bohr: un volumen centenario. Cambridge, Mass: Harvard University Press. ISBN 978-0-674-62415-3.
- ^ Heilbron, John L. (1968). "La dispersión de partículas α y β y el átomo de Rutherford". Archivo de Historia de las Ciencias Exactas . 4 (4): 247–307. doi :10.1007/BF00411591. ISSN 0003-9519. JSTOR 41133273.
- ^ abcdefg Bohr, N. (julio de 1913). "I. Sobre la constitución de átomos y moléculas". Revista filosófica y revista científica de Londres, Edimburgo y Dublín . 26 (151): 1–25. Bibcode :1913PMag...26....1B. doi :10.1080/14786441308634955.
- ^ Rayleigh, Lord (enero de 1906). "VII. Sobre vibraciones eléctricas y la constitución del átomo". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science . 11 (61): 117–123. doi :10.1080/14786440609463428.
- ^ Whittaker, Edmund T. (1989). Una historia de las teorías del éter y la electricidad. 2: Las teorías modernas, 1900-1926 (edición repetida). Nueva York: Dover Publ. ISBN 978-0-486-26126-3.
- ^ abcdefghi Pais, Abraham (2002). Inward bound: de materia y fuerzas en el mundo físico (edición reimpresa). Oxford: Clarendon Press [ua] ISBN 978-0-19-851997-3.
- ^ Bohr, N. (diciembre de 1925). «Teoría atómica y mecánica». Nature . 116 (2927): 845–852. doi :10.1038/116845a0. ISSN 0028-0836.
- ^ Perović, Slobodan (2021). "Líneas espectrales, estados cuánticos y un modelo maestro del átomo". De los datos a los cuantos: la visión de la física de Niels Bohr . Chicago Londres: The University of Chicago Press. ISBN 978-0-226-79833-2.
- ^ abc Giliberti, Marco; Lovisetti, Luisa (2024). "El átomo de hidrógeno de Bohr". Teoría cuántica antigua y mecánica cuántica temprana. Desafíos en la enseñanza de la física. Cham: Springer Nature Switzerland. doi :10.1007/978-3-031-57934-9_6. ISBN 978-3-031-57933-2.
- ^ abc Bohr, Niels (7 de noviembre de 1962). "Niels Bohr – Sesión III" (Entrevista). Entrevista realizada por Thomas S. Kuhn; Leon Rosenfeld; Aage Petersen; Erik Rudinger. Instituto Americano de Física.
- ^ abc Heilbron, John L. (junio de 2013). "El camino hacia el átomo cuántico". Nature . 498 (7452): 27–30. doi :10.1038/498027a. PMID 23739408. S2CID 4355108.
- ^ abcd McCormmach, Russell (1 de enero de 1966). «La teoría atómica de John William Nicholson». Archivo de Historia de las Ciencias Exactas . 3 (2): 160–184. doi :10.1007/BF00357268. JSTOR 41133258. S2CID 120797894.
- ^ ab Nicholson, JW (14 de junio de 1912). "La constitución de la corona solar". Monthly Notices of the Royal Astronomical Society . 72 (8). Oxford University Press: 677–693. doi : 10.1093/mnras/72.8.677 . ISSN 0035-8711.
- ^ ab Bohr, Niels; Rosenfeld, Léon Jacques Henri Constant (1963). Sobre la constitución de átomos y moléculas... Artículos de 1913 reimpresos de la revista Philosophical Magazine, con una introducción de L. Rosenfeld . Copenhague; WA Benjamin: Nueva York. OCLC 557599205.[ página necesaria ]
- ^ Stachel, John (2009). "Bohr y el fotón". Realidad cuántica, causalidad relativista y cierre del círculo epistémico . Dordrecht: Springer. pág. 79.
- ^ Gilder, Louisa (2009). "Los argumentos 1909—1935". La era del entrelazamiento . p. 55.
Bueno, sí", dice Bohr. "Pero difícilmente puedo imaginar que involucre a los cuantos de luz. Mire, incluso si Einstein hubiera encontrado una prueba irrefutable de su existencia y quisiera informarme por telegrama, este telegrama solo me llegaría debido a la existencia y realidad de las ondas de radio.
- ^ "Revelando la conexión oculta entre Pi y el modelo del hidrógeno de Bohr". Physics World . 17 de noviembre de 2015.
- ^ Müller, U.; de Reus, T.; Reinhardt, J.; Müller, B.; Greiner, W. (1988-03-01). "Producción de positrones en haces cruzados de núcleos de uranio desnudo". Physical Review A . 37 (5): 1449–1455. Bibcode :1988PhRvA..37.1449M. doi :10.1103/PhysRevA.37.1449. PMID 9899816. S2CID 35364965.
- ^ Bohr, N. (1985). "El descubrimiento de Rydberg de las leyes espectrales". En Kalckar, J. (ed.). Obras completas . Vol. 10. Ámsterdam: North-Holland Publ. Cy. págs. 373–379.
- ^ Bohr, N. (julio de 1913). "I. Sobre la constitución de átomos y moléculas". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science . 26 (151): 1–25. doi :10.1080/14786441308634955. ISSN 1941-5982.
- ^ Baggott, JE (2013). La historia cuántica: una historia en 40 momentos (Impresión: 3.ª ed.). Oxford: Oxford Univ. Press. ISBN 978-0-19-965597-7.
- ^ ab Baily, C. (1 de enero de 2013). "Modelos atómicos tempranos: de mecánicos a cuánticos (1904-1913)". The European Physical Journal H . 38 (1): 1–38. doi :10.1140/epjh/e2012-30009-7. ISSN 2102-6467.
- ^ Bohr, N. (1913). "Sobre la constitución de átomos y moléculas, Parte II. Sistemas que contienen sólo un núcleo único". Philosophical Magazine . 26 : 476–502.
- ^ Bohr, N. (1 de noviembre de 1913). «LXXIII. Sobre la constitución de átomos y moléculas». The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science . 26 (155): 857–875. Bibcode :1913PMag...26..857B. doi :10.1080/14786441308635031.
- ^ Nicholson, JW (mayo de 1914). "La constitución de átomos y moléculas". Nature . 93 (2324): 268–269. Código Bibliográfico :1914Natur..93..268N. doi :10.1038/093268a0. S2CID 3977652.
- ^ Bury, Charles R. (julio de 1921). "Teoría de Langmuir sobre la disposición de los electrones en átomos y moléculas". Journal of the American Chemical Society . 43 (7): 1602–1609. doi :10.1021/ja01440a023.
- ^ ab Kossel, W. (1916). "Über Molekülbildung als Frage des Atombaus" [Sobre la formación molecular como cuestión de estructura atómica]. Annalen der Physik (en alemán). 354 (3): 229–362. Código Bib : 1916AnP...354..229K. doi : 10.1002/andp.19163540302.
- ^ ab Kragh, Helge (2012). "Lars Vegard, estructura atómica y el sistema periódico" (PDF) . Boletín de Historia de la Química . 37 (1): 42–49. OCLC 797965772. S2CID 53520045. Archivado (PDF) desde el original el 2022-10-09.
- ^ Langmuir, Irving (junio de 1919). "La disposición de los electrones en átomos y moléculas". Revista de la Sociedad Química Americana . 41 (6): 868–934. doi :10.1021/ja02227a002.
- ^ Bohr, Niels (31 de octubre de 1962). "Niels Bohr – Sesión I" (Entrevista). Entrevista realizada por Thomas S. Kuhn; Leon Rosenfeld; Aage Petersen; Erik Rudinger. Instituto Americano de Física.
- ^ Moseley, HGJ (1913). "Los espectros de alta frecuencia de los elementos". Philosophical Magazine . 6.ª serie. 26 : 1024–1034.
- ^ MAB Whitaker (1999). "La síntesis de Bohr-Moseley y un modelo simple para las energías de rayos X atómicos". Revista Europea de Física . 20 (3): 213–220. Bibcode :1999EJPh...20..213W. doi :10.1088/0143-0807/20/3/312. S2CID 250901403.
- ^ van den Broek, Antonius (enero de 1913). "Die Radioelemente, das periodische System und die Konstitution der. Atome". Physikalische Zeitschrift (en alemán). 14 : 32–41.
- ^ Dahl, Jens Peder; Springborg, Michael (10 de diciembre de 1982). "Función espacial de fases y estructura atómica de Wigner: I. El estado fundamental del átomo de hidrógeno". Física molecular . 47 (5): 1001–1019. doi :10.1080/00268978200100752. S2CID 9628509.
- ^ A. Sommerfeld (1916). "Zur Quantentheorie der Spektrallinien". Annalen der Physik (en alemán). 51 (17): 1–94. Código Bib : 1916AnP...356....1S. doi : 10.1002/andp.19163561702.
- ^ W. Wilson (1915). "La teoría cuántica de la radiación y los espectros de líneas". Revista filosófica . 29 (174): 795–802. doi :10.1080/14786440608635362.
- ^ Shaviv, Glora (2010). La vida de las estrellas: el controvertido inicio y surgimiento de la teoría de la estructura estelar . Springer. pág. 203. ISBN 978-3642020872.
- ^ Бор Н. (1970). Избранные научные труды (статьи 1909-1925) . vol. 1. М.: «Наука». pag. 133.
- ^ Svidzinsky, Anatoly A.; Scully, Marlan O.; Herschbach, Dudley R. (23 de agosto de 2005). "Revisión del modelo molecular de Bohr de 1913". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 102 (34): 11985–11988. arXiv : physics/0508161 . Bibcode :2005PNAS..10211985S. doi : 10.1073/pnas.0505778102 . PMC 1186029. PMID 16103360 .
- ^ Schirrmacher, Arne (2009). "Modelo atómico de Bohr". En Greenberger, Daniel M.; Hentschel, Klaus; Weinert, Friedel (eds.). Compendio de física cuántica: conceptos, experimentos, historia y filosofía . Heidelberg Nueva York: Springer. ISBN 978-3-540-70626-7.
- ^ "Directrices para el uso del logotipo". www.iaea.org . 2021-11-23 . Consultado el 2024-09-04 .
Fuentes primarias
- Bohr, N. (julio de 1913). "I. Sobre la constitución de átomos y moléculas". Revista filosófica y revista científica de Londres, Edimburgo y Dublín . 26 (151): 1–25. Bibcode :1913PMag...26....1B. doi :10.1080/14786441308634955.
- Bohr, N. (septiembre de 1913). "XXXVII. Sobre la constitución de átomos y moléculas". Revista filosófica y revista científica de Londres, Edimburgo y Dublín . 26 (153): 476–502. Bibcode :1913PMag...26..476B. doi :10.1080/14786441308634993.
- Bohr, N. (1 de noviembre de 1913). "LXXIII. Sobre la constitución de átomos y moléculas". Revista filosófica y revista científica de Londres, Edimburgo y Dublín . 26 (155): 857–875. Bibcode :1913PMag...26..857B. doi :10.1080/14786441308635031.
- Bohr, N. (octubre de 1913). "Los espectros del helio y el hidrógeno". Nature . 92 (2295): 231–232. Código Bibliográfico :1913Natur..92..231B. doi :10.1038/092231d0. S2CID 11988018.
- Bohr, N. (marzo de 1921). «Estructura atómica». Nature . 107 (2682): 104–107. Código Bibliográfico :1921Natur.107..104B. doi :10.1038/107104a0. S2CID 4035652.
- A. Einstein (1917). "Zum Quantensatz von Sommerfeld und Epstein". Verhandlungen der Deutschen Physikalischen Gesellschaft . 19 : 82–92.Reimpreso en The Collected Papers of Albert Einstein , traductor de A. Engel, (1997) Princeton University Press, Princeton. 6 p. 434. (Proporciona una reformulación elegante de las condiciones de cuantificación de Bohr-Sommerfeld, así como una importante perspectiva sobre la cuantificación de sistemas dinámicos no integrables (caóticos).)
- de Broglie, Mauricio; Langevin, Paul; Solvay, Ernesto; Einstein, Alberto (1912). La théorie du rayonnement et les quanta: rapports et debates de la réunion tenue à Bruxelles, du 30 de octubre al 3 de noviembre de 1911, bajo los auspicios de ME Solvay (en francés). Gauthier-Villars. OCLC 1048217622.
Lectura adicional
- Linus Carl Pauling (1970). "Capítulo 5-1". Química general (3.ª ed.). San Francisco: WH Freeman & Co.
- Reimpresión: Linus Pauling (1988). Química general . Nueva York: Dover Publications. ISBN 0-486-65622-5.
- George Gamow (1985). "Capítulo 2". Treinta años que sacudieron la física . Publicaciones de Dover.
- Walter J. Lehmann (1972). "Capítulo 18". Estructura atómica y molecular: el desarrollo de nuestros conceptos . John Wiley and Sons. ISBN 0-471-52440-9.
- Paul Tipler y Ralph Llewellyn (2002). Física moderna (4.ª ed.). WH Freeman. ISBN 0-7167-4345-0.
- Klaus Hentschel : Elektronenbahnen, Quantensprünge und Spektren, en: Charlotte Bigg y Jochen Hennig (eds.) Atombilder. Ikonografien des Atoms in Wissenschaft und Öffentlichkeit des 20. Jahrhunderts, Göttingen: Wallstein-Verlag 2009, págs. 51–61
- Steven y Susan Zumdahl (2010). "Capítulo 7.4". Química (8.ª ed.). Brooks/Cole. ISBN 978-0-495-82992-8.
- Kragh, Helge (noviembre de 2011). "Objeciones conceptuales a la teoría atómica de Bohr: ¿tienen los electrones 'libre albedrío'?". The European Physical Journal H . 36 (3): 327–352. Bibcode :2011EPJH...36..327K. doi :10.1140/epjh/e2011-20031-x. S2CID 120859582.
Enlaces externos
- Ondas estacionarias en el modelo atómico de Bohr: una simulación interactiva para explicar intuitivamente la condición de cuantificación de las ondas estacionarias en el modo atómico de Bohr
































































