Modelo de reflexión de Blinn-Phong

El modelo de reflexión de Blinn-Phong , también llamado modelo de reflexión de Phong modificado, es una modificación desarrollada por Jim Blinn del modelo de reflexión de Phong . ^[1]

Blinn–Phong es un modelo de sombreado utilizado en la tubería de función fija de OpenGL y Direct3D (antes de Direct3D 10 y OpenGL 3.1), y se lleva a cabo en cada vértice a medida que pasa por la tubería de gráficos ; los valores de píxeles entre los vértices se interpolan mediante sombreado Gouraud de forma predeterminada, en lugar del sombreado Phong , que es computacionalmente más costoso . ^[2]

En el sombreado Phong, uno debe recalcular continuamente el producto escalar entre un espectador ( V ) y el haz de una fuente de luz ( L ) reflejado ( R ) sobre una superficie.${\displaystyle R\cdot V}$

Si, en cambio, se calcula un vector intermedio entre los vectores del espectador y de la fuente de luz,

${\displaystyle H={\frac {L+V}{\izquierda\|L+V\derecha\|}}}$

${\displaystyle R\cdot V}$se puede reemplazar con , donde es la normal de superficie normalizada . En la ecuación anterior, y son ambos vectores normalizados, y es una solución de la ecuación donde es la matriz Householder que refleja un punto en el hiperplano que contiene el origen y tiene la normal${\displaystyle N\cdot H}$${\estilo de visualización N}$${\estilo de visualización L}$${\estilo de visualización V}$${\estilo de visualización H}$${\displaystyle V=P_{H}(-L),}$$Estilo de visualización P_{H}}$${\estilo de visualización H.}$

Este producto escalar representa el coseno de un ángulo que es la mitad del ángulo representado por el producto escalar de Phong si V , L , N y R se encuentran todos en el mismo plano. Esta relación entre los ángulos sigue siendo aproximadamente cierta cuando los vectores no se encuentran en el mismo plano, especialmente cuando los ángulos son pequeños. Por lo tanto, el ángulo entre N y H a veces se denomina ángulo medio.

Teniendo en cuenta que el ángulo entre el vector medio y la normal de la superficie es probable que sea menor que el ángulo entre R y V utilizado en el modelo de Phong (a menos que la superficie se vea desde un ángulo muy pronunciado para el cual es probable que sea mayor), y dado que Phong está utilizando un exponente que se puede establecer de manera que esté más cerca de la expresión anterior.${\displaystyle \left(R\cdot V\right)^{\alpha },}$${\displaystyle \alpha ^{\prime }>\alpha }$${\displaystyle \left(N\cdot H\right)^{\alpha ^{\prime }}}$

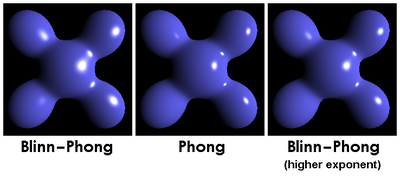
En el caso de superficies iluminadas desde el frente (reflejos especulares en superficies que miran al observador), se obtendrán reflejos especulares que se asemejarán mucho a los correspondientes reflejos Phong. Sin embargo, mientras que los reflejos Phong son siempre redondos para una superficie plana, los reflejos Blinn-Phong se vuelven elípticos cuando la superficie se observa desde un ángulo pronunciado. Esto se puede comparar con el caso en el que el sol se refleja en el mar cerca del horizonte, o cuando una farola lejana se refleja en el pavimento mojado, donde el reflejo siempre será mucho más extendido verticalmente que horizontalmente. ^[3]${\displaystyle \alpha ^{\prime }=4\,\alpha }$

Además, si bien puede verse como una aproximación al modelo Phong, produce modelos más precisos de funciones de distribución de reflectancia bidireccional determinadas empíricamente que Phong para muchos tipos de superficies. ^[4]

Blinn-Phong será más rápido que Phong en el caso en que el observador y la luz se consideren muy remotos, como acercándose o en el infinito. Este es el caso de las luces direccionales y las cámaras ortográficas/isométricas. En este caso, el vector intermedio es independiente de la posición y la curvatura de la superficie simplemente porque el vector intermedio depende de la dirección de la posición del observador y de la dirección de la posición de la luz, que convergen individualmente a esta distancia remota, por lo tanto, el vector intermedio puede considerarse constante en este caso. por lo tanto, se puede calcular una vez para cada luz y luego se puede utilizar para todo el cuadro, o incluso mientras la luz y el punto de vista permanezcan en la misma posición relativa. Lo mismo no es cierto con el método de Phong de utilizar el vector de reflexión que depende de la curvatura de la superficie y debe recalcularse para cada píxel de la imagen (o para cada vértice del modelo en el caso de la iluminación de vértice). En escenas 3D con cámaras en perspectiva, esta optimización no es posible.${\estilo de visualización H}$

Este ejemplo en lenguaje de sombreado de alto nivel es un método para determinar la luz difusa y especular a partir de una luz puntual. Se pasan por la estructura de la luz, la posición en el espacio de la superficie, el vector de dirección de la vista y la normal de la superficie. Se devuelve una estructura de iluminación;

Lo que sigue también debe fijar ciertos productos escalares en cero en el caso de respuestas negativas. Sin eso, la luz que se aleja de la cámara se trata de la misma manera que la luz que se acerca a ella. Para el cálculo especular, un "halo" incorrecto de luz que se refleja en los bordes de un objeto y se aleja de la cámara puede parecer tan brillante como la luz que se refleja directamente hacia la cámara.

estructura Iluminación { float3 Difuso ; float3 Especular ; };     struct PointLight { float3 posición ; float3 colordifuso ; float potenciadifusa ; float3 colorespeculares ; float potenciaespeculares ; };      Iluminación GetPointLight ( PointLight light , float3 pos3D , float3 viewDir , float3 normal ) { Iluminación OUT ; if ( light.diffusePower > 0 ) { float3 lightDir = light.position - pos3D ; //Posición 3D en el espacio de la superficie float distance = length ( lightDir ); lightDir = lightDir / distance ; // = normalize( lightDir ) ; distance = distance * distance ;                              //Intensidad de la luz difusa. Saturar para mantener dentro del rango 0-1. float NdotL = dot ( normal , lightDir ); float spreadIntensity = saturate ( NdotL );       // Calcula la luz difusa teniendo en cuenta el color de la luz, la potencia y la atenuación OUT . Diffuse = spreadIntensity * light . spreadColor * light . spreadPower / distance ;        //Calcula el semivector entre el vector de luz y el vector de vista. float3 H = normalize ( lightDir + viewDir );     //Intensidad de la luz especular float NdotH = dot ( normal , H ); float specularIntensity = pow ( saturate ( NdotH ), specularHardness );        //Suma la factorización de luz especular OUT . Specular = specularIntensity * light . specularColor * light . specularPower / distance ; } return OUT ; }          

Este ejemplo del lenguaje de sombreado OpenGL consta de dos archivos de código o shaders . El primero es un denominado shader de vértices e implementa el sombreado Phong , que se utiliza para interpolar la normal de la superficie entre los vértices. El segundo shader es un denominado shader de fragmentos e implementa el modelo de sombreado Blinn–Phong para determinar la luz difusa y especular de una fuente de luz puntual.

Este sombreador de vértices implementa el sombreado Phong :

atributo vec3 inputPosition ; atributo vec3 inputNormal ;    proyección mat4 uniforme , modelview , normalMat ;    variando vec3 normalInterp ; variando vec3 vertPos ;    void main () { gl_Position = proyección * modelview * vec4 ( entradaPosition , 1.0 ); vec4 vertPos4 = modelview * vec4 ( entradaPosition , 1.0 ); vertPos = vec3 ( vertPos4 ) / vertPos4.w ; normalInterp = vec3 ( normalMat * vec4 ( entradaNormal , 0.0 ) ) ; }                            

Este sombreador de fragmentos implementa el modelo de sombreado Blinn-Phong ^[5] y la corrección gamma :

precisión mediap float ;  en vec3 normalInterp ; en vec3 vertPos ;    modo int uniforme ;  const vec3 lightPos = vec3 ( 1.0 , 1.0 , 1.0 ); const vec3 lightColor = vec3 ( 1.0 , 1.0 , 1.0 ); const float lightPower = 40.0 ; const vec3 ambientColor = vec3 ( 0.1 , 0.0 , 0.0 ); const vec3 spreadColor = vec3 ( 0.5 , 0.0 , 0.0 ); const vec3 specColor = vec3 ( 1.0 , 1.0 , 1.0 ); const float shininess = 16.0 ; const float screenGamma = 2.2 ; // Suponga que el monitor está calibrado al espacio de color sRGB                                           vacío principal () {   vec3 normal = normalizar ( normalInterp ); vec3 lightDir = lightPos - vertPos ; float distancia = punto ( lightDir , lightDir ); lightDir = normalizar ( lightDir );                  flotante lambertiano = máx ( punto ( lightDir , normal ), 0.0 ); flotante especular = 0.0 ;          si ( lambertiano > 0,0 ) {     vec3 viewDir = normalizar ( - vertPos );    // esto es blinn phong vec3 halfDir = normalize ( lightDir + viewDir ); float specAngle = max ( dot ( halfDir , normal ), 0.0 ); specular = pow ( specAngle , shininess ); // esto es phong (para comparación) if ( mode == 2 ) { vec3 reflectDir = reflect ( -lightDir , normal ); specAngle = max ( dot ( reflejadDir , viewDir ), 0.0 ); // tenga en cuenta que el exponente es diferente aquí specular = pow ( specAngle , shininess / 4.0 ); } } vec3 colorLinear = ambientColor + spreadColor * lambertian * lightColor * lightPower / distance + specColor * specular * lightColor * lightPower / distance ; // aplicar corrección gamma (suponer que ambientColor, spreadColor y specColor // han sido linealizados, es decir, no tienen corrección gamma en ellos) vec3 colorGammaCorrected = pow ( colorLinear , vec3 ( 1.0 / screenGamma )); // usar el color con corrección gamma en el fragmento gl_FragColor = vec4 ( colorGammaCorrected , 1.0 ); }                                                                              

No se supone que los colores ambientColor , spreadColor y specColor estén corregidos por gamma . Si son colores obtenidos de archivos de imagen con corrección gamma ( JPEG , PNG , etc.), deben linealizarse antes de trabajar con ellos, lo que se hace escalando los valores del canal al rango [0, 1] y elevándolos al valor gamma de la imagen, que para imágenes en el espacio de color sRGB se puede suponer que es aproximadamente 2,2 (aunque para este espacio de color específico, una simple relación de potencia es solo una aproximación de la transformación real ). Las API de gráficos modernas tienen la capacidad de realizar esta corrección gamma automáticamente al muestrear desde una textura o escribir en un framebuffer . ^[6]

• Lista de algoritmos de sombreado comunes
• Modelo de reflexión de Phong para el modelo correspondiente de Phong
• Corrección gamma
• Resaltado especular