Modelo de reactor de flujo de pistón

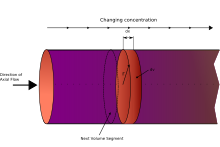
El modelo de reactor de flujo pistón ( PFR , a veces llamado reactor tubular continuo , CTR , o reactor de flujo pistón ) es un modelo utilizado para describir reacciones químicas en sistemas continuos de flujo de geometría cilíndrica. El modelo PFR se utiliza para predecir el comportamiento de reactores químicos de dicho diseño, de modo que se puedan estimar variables clave del reactor, como las dimensiones del mismo.

El fluido que pasa a través de un PFR puede modelarse como si fluyera a través del reactor como una serie de "tapones" coherentes infinitamente delgados, cada uno con una composición uniforme, que viajan en la dirección axial del reactor, y cada tapón tiene una composición diferente de los anteriores y posteriores. La suposición clave es que cuando un tapón fluye a través de un PFR, el fluido se mezcla perfectamente en la dirección radial pero no en la dirección axial (hacia adelante o hacia atrás). Cada tapón de volumen diferencial se considera como una entidad separada, efectivamente un reactor de tanque agitado continuo infinitesimalmente pequeño , que limita el volumen a cero. A medida que fluye por el PFR tubular, el tiempo de residencia ( ) del tapón es una función de su posición en el reactor. En el PFR ideal, la distribución del tiempo de residencia es, por lo tanto, una función delta de Dirac con un valor igual a .${\estilo de visualización \tau}$${\estilo de visualización \tau}$

La PFR estacionaria se rige por ecuaciones diferenciales ordinarias , cuya solución se puede calcular siempre que se conozcan las condiciones de contorno apropiadas.

El modelo PFR funciona bien para muchos fluidos: líquidos, gases y lodos. Aunque el flujo turbulento y la difusión axial causan un cierto grado de mezcla en la dirección axial en los reactores reales, el modelo PFR es adecuado cuando estos efectos son lo suficientemente pequeños como para que se puedan ignorar.

En el caso más simple de un modelo PFR, se deben hacer varias suposiciones clave para simplificar el problema, algunas de las cuales se describen a continuación. Tenga en cuenta que no todas estas suposiciones son necesarias, sin embargo, la eliminación de estas suposiciones aumenta la complejidad del problema. El modelo PFR se puede utilizar para modelar reacciones múltiples, así como reacciones que involucran cambios de temperatura, presión y densidad del flujo. Aunque estas complicaciones se ignoran en lo que sigue, a menudo son relevantes para los procesos industriales.

Supuestos:

• Flujo de tapón
• Estado estable
• Densidad constante (razonable para algunos líquidos pero con un error del 20 % para polimerizaciones; válida para gases solo si no hay caída de presión, ni cambio neto en el número de moles, ni ningún cambio grande de temperatura)
• Reacción única que ocurre en la mayor parte del fluido (de forma homogénea).

Un balance de materia sobre el volumen diferencial de un elemento fluido, o tapón, sobre la especie i de longitud axial dx entre x y x + dx da:

[acumulación] = [entrada] - [salida] + [generación] - [consumo]

La acumulación es 0 en estado estable; por lo tanto, el balance de masa anterior se puede reescribir de la siguiente manera:

1. . ^[1]${\displaystyle F_{i}(x)-F_{i}(x+dx)+A_{t}dx\nu _{i}r=0}$

dónde:

• x es la posición axial del tubo del reactor, m
• dx el espesor diferencial del tapón de fluido
• El índice i se refiere a la especie i
• F _i (x) es el caudal molar de la especie i en la posición x , mol/s
• D es el diámetro del tubo, m
• A _t es el área de la sección transversal del tubo, ^m2
• ν es el coeficiente estequiométrico , adimensional
• r es el término fuente/sumidero volumétrico (la velocidad de reacción), mol/m ³ s.

La velocidad lineal del flujo, u (m/s) y la concentración de la especie i , C _i (mol/m ³ ) se pueden introducir como:

${\displaystyle u={\frac {\dot {v}}{A_{t}}}={\frac {4{\dot {v}}}{\pi D^{2}}}}$ y ${\displaystyle F_{i}=A_{t}uC_{i}\,}$

¿Dónde está el caudal volumétrico?${\displaystyle {\punto {v}}}$

Aplicando lo anterior a la ecuación 1, el balance de masa en i se convierte en:

2. . ^[1]${\displaystyle A_{t}u[C_{i}(x)-C_{i}(x+dx)]+A_{t}dx\nu _{i}r=0\,}$

Cuando se cancelan los términos iguales y se aplica el límite dx → 0 a la ecuación 2, el balance de masa de la especie i se convierte en

3. , ^[1]${\displaystyle u{\frac {dC_{i}}{dx}}=\nu _{i}r}$

La dependencia de la temperatura de la velocidad de reacción, r , se puede estimar utilizando la ecuación de Arrhenius . En general, a medida que aumenta la temperatura, también lo hace la velocidad a la que se produce la reacción. El tiempo de residencia, , es la cantidad promedio de tiempo que una cantidad discreta de reactivo pasa dentro del tanque.${\estilo de visualización \tau}$

Asumir:

• condiciones isotérmicas o temperatura constante (k es constante)
• reacción única e irreversible (ν _A = -1)
• reacción de primer orden (r = k C _A )

Después de integrar la ecuación 3 utilizando los supuestos anteriores, resolviendo C _A (x), obtenemos una ecuación explícita para la concentración de la especie A en función de la posición:

4. ,${\displaystyle C_{A}(x)=C_{A0}e^{-k\tau }\,}$

donde C _A0 es la concentración de la especie A en la entrada del reactor, que surge de la condición de borde de integración.

Los PFR se utilizan para modelar la transformación química de los compuestos a medida que se transportan en sistemas que se asemejan a "tuberías". La "tubería" puede representar una variedad de conductos naturales o diseñados a través de los cuales fluyen líquidos o gases (por ejemplo, ríos, tuberías, regiones entre dos montañas, etc.).

Un reactor de flujo tapón ideal tiene un tiempo de residencia fijo: cualquier fluido (tapón) que entre en el reactor en el momento saldrá del reactor en el momento , donde es el tiempo de residencia del reactor. Por lo tanto, la función de distribución del tiempo de residencia es una función delta de Dirac en . Un reactor de flujo tapón real tiene una distribución del tiempo de residencia que es un pulso estrecho alrededor de la distribución del tiempo de residencia medio .${\estilo de visualización t}$${\estilo de visualización t+\tau}$${\estilo de visualización \tau}$${\estilo de visualización \tau}$

Un reactor de flujo tapón típico podría ser un tubo lleno de algún material sólido (con frecuencia un catalizador ). Por lo general, este tipo de reactores se denominan reactores de lecho empacado o PBR. A veces, el tubo será un tubo en un intercambiador de calor de carcasa y tubo .

Cuando no se puede aplicar un modelo de flujo de tapón, se suele emplear el modelo de dispersión. ^{[2] [3]}

La distribución del tiempo de residencia (RTD) de un reactor es una característica de la mezcla que se produce en el reactor químico. En un reactor de flujo pistón no hay mezcla axial y esta omisión se refleja en la RTD que presentan esta clase de reactores. ^[4]

Los reactores de flujo tapón reales no satisfacen los patrones de flujo idealizados, el flujo de retromezcla o la desviación del flujo tapón del comportamiento ideal pueden deberse a la canalización del fluido a través del recipiente, al reciclado del fluido dentro del recipiente o a la presencia de una región estancada o zona muerta de fluido en el recipiente. ^[5] También se han modelado reactores de flujo tapón reales con comportamiento no ideal. ^[6] Para predecir el comportamiento exacto de un recipiente como reactor químico , se utiliza la técnica RTD o de respuesta al estímulo. La técnica del trazador , el método más utilizado para el estudio de la dispersión axial, se suele utilizar en forma de: ^[7]

• Entrada de pulso
• Entrada de pasos
• Entrada cíclica
• Entrada aleatoria

La RTD se determina experimentalmente inyectando una sustancia química, molécula o átomo inerte, llamado trazador, en el reactor en algún momento t = 0 y luego midiendo la concentración del trazador, C, en la corriente de efluente en función del tiempo. ^[4]

La curva RTD del fluido que sale de un recipiente se denomina curva E. Esta curva está normalizada de tal manera que el área debajo de ella es la unidad:

(1)

${\displaystyle \int E\parcial t=1}$

La edad media de la corriente de salida o el tiempo medio de residencia es:

(2)

${\displaystyle \tau =\int tE\parcial t=\suma tE\nabla t}$

Cuando se inyecta un trazador en un reactor en un lugar a más de dos o tres diámetros de partículas aguas abajo de la entrada y se mide a cierta distancia aguas arriba de la salida, el sistema se puede describir mediante el modelo de dispersión con combinaciones de condiciones de contorno abiertas o cerradas. ^[3] Para un sistema en el que no hay discontinuidad en el tipo de flujo en el punto de inyección del trazador o en el punto de medición del trazador, la varianza para el sistema abierto-abierto es:

(3)

${\displaystyle (\sigma _{\theta})^{2}=(\sigma _{t})^{2}/\tau ^{2}=2/P_{e}+8/(P_{e})^{2}}$

Dónde,

(4)

${\displaystyle P_{e}=LU/D_{L}}$

que representa la relación entre la velocidad de transporte por convección y la velocidad de transporte por difusión o dispersión.

${\estilo de visualización L}$= longitud característica (m)

$Estilo de visualización D_{L}}$= coeficiente de dispersión efectivo (m ² /s)

${\estilo de visualización U}$= velocidad superficial (m/s) basada en la sección transversal vacía

El número de dispersión del buque se define como:

${\displaystyle 1/P_{e}=D_{L}/LU}$

La varianza de una distribución continua medida en un número finito de ubicaciones equidistantes viene dada por:

(5)

${\displaystyle (\sigma _{t})^{2}=\suma t_{i}^{2}C_{i}/\suma C_{i}-\suma [t_{i}C_{i}/\suma C_{i}]^{2}}$

Donde el tiempo de residencia medio τ viene dado por:

(6)

${\displaystyle \tau =\suma t_{i}C_{i}/\suma C_{i}}$

(7)

${\displaystyle (\sigma _{\theta})^{2}=(\sigma _{t})^{2}/\tau ^{2}}$

Por lo tanto, (σ _θ ) ² se puede evaluar a partir de los datos experimentales sobre C vs. t y, para valores conocidos de , el número de dispersión se puede obtener de la ecuación (3) como:${\displaystyle (\sigma _{\theta })^{2}}$${\displaystyle (1/P_{e})}$

(8)

${\displaystyle D_{L}/LU={-1+{\sqrt {1+8(\sigma _{\theta })^{2}}} \sobre 8}}$

De esta manera se puede estimar el coeficiente de dispersión axial DL _{( L = altura empaquetada)} ^[5]

Como se mencionó anteriormente, también hay otras condiciones de contorno que se pueden aplicar al modelo de dispersión y que dan diferentes relaciones para el número de dispersión. ^{[8] [9] [3]}

Ventajas

Desde el punto de vista técnico de seguridad, el PFR tiene las ventajas de ^[10]

1. Funciona en estado estable.
2. Es bien controlable
3. Se pueden instalar grandes áreas de transferencia de calor .

Preocupaciones

Los principales problemas radican en las difíciles y a veces críticas operaciones de arranque y parada. ^[10]

Los reactores de flujo tapón se utilizan para algunas de las siguientes aplicaciones:

• Producción a gran escala
• Reacciones rápidas
• Reacciones homogéneas o heterogéneas
• Producción continua
• Reacciones de alta temperatura