Milla náutica

Milla náutica
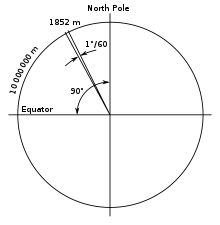Definición histórica: 1 milla náutica
información general
Unidad de	longitud
Símbolo	M, NM, [a] o nmi
Conversiones
1 M, NM, [a] o nmi en...	... es igual a...
metro	1.852 [1]
pie	≈ 6.076,11549
milla estatutaria	≈ 1,15078
cable	10

Una milla náutica es una unidad de longitud utilizada en la navegación aérea, marítima y espacial , y para la definición de aguas territoriales . ^{[2] [3] [4]} Históricamente, se definió como la longitud del arco meridiano correspondiente a un minuto ( ⁠1/60⁠ de un grado) de latitud en el ecuador, de modo que la circunferencia polar de la Tierra está muy cerca de 21.600 millas náuticas (es decir, 60 minutos × 360 grados). Hoy en día, la milla náutica internacional se define como 1.852 metros (aproximadamente 6.076 pies; 1,151 millas). ^[5] La unidad derivada de velocidad es el nudo , una milla náutica por hora.

No existe un único símbolo acordado internacionalmente, pero se utilizan varios. ^[1]

• El NM es utilizado por la Organización de Aviación Civil Internacional . ^{[6] [7]}
• nmi es utilizado por el Instituto de Ingenieros Eléctricos y Electrónicos ^[8] y la Oficina de Publicaciones del Gobierno de los Estados Unidos . ^[9]
• La Organización Hidrográfica Internacional utiliza M como abreviatura de milla náutica . ^[10]
• nm es una abreviatura no estándar utilizada en muchas aplicaciones y textos marítimos, incluidos los de los pilotos costeros y las instrucciones de navegación del gobierno de EE. UU. ^[11] Entra en conflicto con el símbolo SI para nanómetro .

La palabra milla proviene de la frase latina que significa mil pasos: mille passus . La navegación en el mar se hacía a ojo ^[12] hasta alrededor de 1500, cuando se desarrollaron instrumentos de navegación y los cartógrafos comenzaron a utilizar un sistema de coordenadas con paralelos de latitud y meridianos de longitud .

La primera referencia de 60 millas por grado es un mapa de Nicolaus Germanus en una edición de 1482 de la Geografía de Ptolomeo que indica que un grado de longitud en el Ecuador contiene " milaria 60 ". ^[13] Un mapa manuscrito anterior de Nicolaus Germanus en una edición anterior de Geografía dice " unul gradul log. et latitud sub equinortiali formet stadia 500 que fanut miliaria 62 ⁠1/2⁠ " ("un grado de longitud y latitud bajo el ecuador forma 500estadios, que suman 62⁠1/2⁠ millas"). ^[14] Ya sea una corrección o conveniencia, la razón del cambio de 62 ⁠1/2⁠ No se explica la relación de 60 millas por grado. Finalmente, la relación de 60 millas por grado apareció en inglés en una traducción de 1555 de las Décadas de Pietro Martire d'Anghiera : "[Ptolomeo] asignó igualmente a cada grado treinta kilómetros". ^[15]

A finales del siglo XVI, los geógrafos y navegantes ingleses sabían que la relación entre las distancias en el mar y los grados era constante a lo largo de cualquier círculo máximo (como el ecuador o cualquier meridiano), suponiendo que la Tierra fuera una esfera. En 1574, William Bourne enunció en A Regiment for the Sea la "regla para elevar un grado" practicada por los navegantes: "Pero, tal como yo lo entiendo, en Inglaterra deberíamos permitir 60 millas por grado: es decir, después de 3 millas por una de nuestras leguas inglesas, por lo que 20 de nuestras leguas inglesas deberían corresponder a un grado". ^[16] Asimismo, Robert Hues escribió en 1594 que la distancia a lo largo de un círculo máximo era de 60 millas por grado. ^[17] Sin embargo, estos se referían a la antigua milla inglesa de 5000 pies y la legua de 15 000 pies, basándose en la subestimación de Ptolomeo de la circunferencia de la Tierra . ^[18] A principios del siglo XVII, los geógrafos ingleses comenzaron a reconocer la discrepancia entre la medición angular de un grado de latitud y la medición lineal de millas. En 1624, Edmund Gunter sugirió 352.000 pies por grado (5866 ⁠2/3⁠ pies por minuto de arco ). ^{[19] [17]} En 1633, William Oughtred sugirió 349.800 pies por grado (5830 pies por minuto de arco). ^[20] Tanto Gunter como Oughtred propusieron la noción de dividir un grado en 100 partes, pero su propuesta fue generalmente ignorada por los navegantes. La relación de 60 millas, o 20 leguas, por grado de latitud permaneció fija mientras que la longitud de la milla fue revisada con mejores estimaciones de la circunferencia de la Tierra. En 1637, Robert Norwood propuso una nueva medida de 6120 pies por minuto de arco de latitud, que estaba a 44 pies del valor actualmente aceptado para una milla náutica. ^[21]

Como la Tierra no es una esfera perfecta sino un esferoide achatado con polos ligeramente aplanados, un minuto de latitud no es constante, sino unos 1.862 metros en los polos y 1.843 metros en el ecuador. ^[22] Francia y otros países métricos afirman que, en principio, una milla náutica es un minuto de arco de un meridiano a una latitud de 45°, pero esa es una justificación moderna para un cálculo más mundano que se desarrolló un siglo antes. A mediados del siglo XIX, Francia había definido una milla náutica a través de la definición original de 1791 del metro , una diezmillonésima parte de un cuarto de meridiano . ^{[23] [24]} Entonces ⁠10.000.000 metros/90 × 60⁠ = 1.851,85 m ≈ 1.852 m se convirtió en la longitud métrica de una milla náutica. Francia la legalizó para la Armada francesa en 1906, y muchos países métricos votaron para sancionarla para uso internacional en la Conferencia Hidrográfica Internacional de 1929. ^{[ cita requerida ]}

Tanto Estados Unidos como el Reino Unido utilizaron un minuto de arco promedio, específicamente, un minuto de arco de un círculo máximo de una esfera que tiene la misma área de superficie que el elipsoide Clarke 1866. [ ^25] El radio autálico (de igual área) del elipsoide Clarke 1866 es 6.370.997,2 metros (20.902.222 pies). ^[26] El minuto de arco resultante es 1.853,2480 metros (6.080,210 pies). Estados Unidos eligió cinco dígitos significativos para su milla náutica, 6.080,2 pies , mientras que el Reino Unido eligió cuatro dígitos significativos para su milla del Almirantazgo, 6.080 pies.

En 1929, la Primera Conferencia Hidrográfica Internacional Extraordinaria en Mónaco definió la milla náutica internacional como exactamente 1.852 metros (que son 6.076,12 pies). ^[1] Estados Unidos no adoptó la milla náutica internacional hasta 1954. ^[27] Gran Bretaña la adoptó en 1970, ^[28] pero las referencias legales a la unidad obsoleta ahora se convierten a 1.853 metros (que son 6.079,40 pies). ^[29]

El metro se definió originalmente como 1 ⁄ 10.000.000 de la longitud del arco meridiano desde el polo norte hasta el ecuador (1% de un grado centesimal de latitud), ^[b] por lo que un kilómetro de distancia corresponde a un centígrado (también conocido como minuto de arco centesimal) de latitud. La circunferencia de la Tierra es, por tanto, de aproximadamente 40.000 km. La circunferencia ecuatorial es ligeramente más larga que la circunferencia polar; la medida basada en esto ( ⁠40.075,017 kilómetros/360 × 60⁠ = 1.855,3 metros) se conoce como la milla geográfica .

Usando la definición ⁠1/60⁠ de un grado de latitud en Marte , una milla náutica marciana equivale a 983 m (1075 yardas). Esto es potencialmente útil para la navegación celestial en una misión humana al planeta , tanto como una abreviatura y una forma rápida de determinar aproximadamente la ubicación. ^[31]

• Milla náutica medida
• Conversión de unidades
• Órdenes de magnitud (longitud)