Miliradián
Este artículo necesita citas adicionales para su verificación . ( abril de 2021 ) |
| Miliradián | |
|---|---|
 La retícula PSO-1 de un rifle francotirador Dragunov tiene marcas con un espaciado de 1 mrad, que se pueden usar para compensar la deriva del viento, la corrección del impacto o la estimación del alcance . | |
| información general | |
| Sistema de unidades | Unidad derivada del SI |
| Unidad de | Ángulo |
| Símbolo | mil, mil |
| Llamado en honor a | El prefijo métrico mili- (del latín mille que significa "mil") y el radián |
| En unidades | Adimensional con una longitud de arco de una milésima parte del radio, es decir 1mm/metro o 1 metro/kilómetros |
| Conversiones | |
| 1mrad en... | ... es igual a... |
| radianes | 1/1000 genial |
| vueltas | 1/2000 π girar |
| gones | 1/5 π ≈ 0,063662 gramos |
| grados | 9/50 π ≈ 0,057296° |
| minutos de arco | 54/5 π ≈ 3.4377′ |
Un milirradián ( símbolo SI mrad , a veces también abreviado mil ) es una unidad derivada del SI para la medición angular que se define como una milésima de radián (0,001 radián). Los milirradianes se utilizan para ajustar las miras de las armas de fuego ajustando el ángulo de la mira en comparación con el cañón (arriba, abajo, izquierda o derecha). Los milirradianes también se utilizan para comparar agrupaciones de disparos o para comparar la dificultad de dar en el blanco a diferentes distancias. Cuando se utiliza una mira con ajuste en mrad y una retícula con marcas en mrad (llamada "mira mrad/mrad"), el tirador puede usar la retícula como una regla para contar la cantidad de mrads que un disparo se desvió del objetivo, lo que se traduce directamente en el ajuste de la mira necesario para dar en el blanco con un disparo de seguimiento. Las ópticas con marcas mrad en la retícula también se pueden utilizar para hacer una estimación de la distancia de un objetivo de tamaño conocido, o viceversa, para determinar el tamaño de un objetivo si se conoce la distancia, una práctica denominada "fresado".
Los milirradianes se utilizan generalmente para ángulos muy pequeños, lo que permite aproximaciones matemáticas muy precisas para calcular más fácilmente con proporciones directas , de ida y vuelta entre la separación angular observada en una óptica, la subtensión lineal en el objetivo y el alcance. En tales aplicaciones, es útil utilizar una unidad para el tamaño del objetivo que sea una milésima parte de la unidad de alcance, por ejemplo, utilizando las unidades métricas milímetros para el tamaño del objetivo y metros para el alcance. Esto coincide con la definición del milirradián, donde la longitud del arco se define como 1/1.000 del radio. Un valor de ajuste común en las miras de armas de fuego es 1 cm a 100 metros, lo que equivale a 10 milímetros/100 metros = 1/10 señor.
La verdadera definición de un milirradián se basa en un círculo unitario con un radio de uno y un arco dividido en 1000 mrad por radián, por lo tanto, 2000 π o aproximadamente 6283,185 milirradianes en una vuelta , y los ajustes de las miras telescópicas y las retículas están calibrados según esta definición. [1] También hay otras definiciones utilizadas para la cartografía terrestre y la artillería que se redondean para dividirse más fácilmente en partes más pequeñas para su uso con brújulas , que a menudo se denominan "mils", "líneas" o similares. Por ejemplo, hay miras de artillería y brújulas con 6400 mils de la OTAN , 6000 mils del Pacto de Varsovia o 6300 "streck" suecos por vuelta en lugar de 360° o 2π radianes, logrando una resolución mayor que una brújula de 360° y al mismo tiempo siendo más fácil de dividir en partes que si se usaran miliradianes verdaderos.
Historia

El milirradián (aproximadamente 6283,185 en un círculo) fue utilizado por primera vez a mediados del siglo XIX por Charles-Marc Dapples (1837-1920), un ingeniero suizo y profesor de la Universidad de Lausana . [2] Los grados y los minutos eran las unidades habituales de medición angular, pero se propusieron otras, como los " grads " (400 gradianes en un círculo) con diversos nombres que tenían una considerable popularidad en gran parte del norte de Europa. Sin embargo, la Rusia imperial utilizó un enfoque diferente, dividiendo un círculo en triángulos equiláteros (60° por triángulo, 6 triángulos en un círculo) [ cita requerida ] y, por lo tanto, 600 unidades por círculo.
En la época del inicio de la Primera Guerra Mundial , Francia estaba experimentando con el uso de milièmes o milésimas angulares (6400 en un círculo) para su uso con miras de artillería en lugar de decígrados (4000 en un círculo). El Reino Unido también los estaba probando para reemplazar grados y minutos. Fueron adoptados por Francia, aunque los decígrados también se mantuvieron en uso durante la Primera Guerra Mundial. Otras naciones también utilizaron decígrados. Estados Unidos, que copió muchas prácticas de artillería francesa, adoptó milésimas angulares, más tarde conocidas como milésimas de la OTAN . Antes de 2007, las fuerzas de defensa suecas usaban "streck" (6300 en un círculo, streck significa líneas o marcas) (junto con grados para cierta navegación) que está más cerca del milirradián pero luego cambió a milésimas de la OTAN. Después de la Revolución bolchevique y la adopción del sistema métrico de medición (por ejemplo, la artillería reemplazó las "unidades de base" por metros), el Ejército Rojo expandió el círculo de 600 unidades a un círculo de 6000 milésimas. Por lo tanto, el mil ruso tiene un origen algo diferente de aquellos derivados de las prácticas de artillería francesa.
En la década de 1950, la OTAN adoptó las unidades métricas de medida para uso terrestre y general. Los milímetros, metros y kilogramos de la OTAN se convirtieron en el estándar, aunque los grados siguieron utilizándose para fines navales y aéreos, lo que reflejaba las prácticas civiles.
Principio matemático
Derecha : Un milirradián corresponde a 1/1000 del ángulo de un radián. (La imagen de la derecha está exagerada para ilustrarlo, ya que un milirradián es mucho más pequeño en realidad).
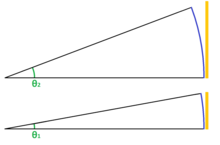
El uso del milirradián es práctico porque se relaciona con ángulos pequeños y, cuando se utilizan radianes, la aproximación de ángulos pequeños muestra que el ángulo se aproxima al seno del ángulo, es decir , . Esto permite al usuario prescindir de la trigonometría y utilizar proporciones simples para determinar el tamaño y la distancia con gran precisión para cálculos de rifles y artillería de corta distancia utilizando la práctica propiedad de subtensión: un mrad subtiende aproximadamente un metro a una distancia de mil metros .
Más en detalle, porque , en lugar de encontrar la distancia angular denotada por θ (letra griega theta ) utilizando la función tangente
- ,
En cambio, se puede hacer una buena aproximación utilizando la definición de radián y la fórmula simplificada:
Dado que un radián se define matemáticamente como el ángulo formado cuando la longitud de un arco circular es igual al radio del círculo, un milirradián es el ángulo formado cuando la longitud de un arco circular es igual a1/1000 del radio del círculo. Al igual que el radián, el milirradián es adimensional , pero a diferencia del radián, donde se debe usar la misma unidad para el radio y la longitud del arco, el milirradián necesita tener una relación entre las unidades donde la subtensión es una milésima del radio cuando se usa la fórmula simplificada.
Error de aproximación
El error de aproximación al utilizar la fórmula lineal simplificada aumentará a medida que aumenta el ángulo. Por ejemplo, un
- 3,3 × 10 −7 % (o3,3 partes por mil millones) de error para un ángulo de 0,1 mrad, por ejemplo, suponiendo que 0,1 mrad equivale a 1 cm a 100 m [3]
- Error del 0,03 % para 30 mrad, es decir, suponiendo que 30 mrad equivalen a 30 m a 1 km [4]
- Error del 2,9 % para 300 mrad, es decir, suponiendo que 300 mrad equivalen a 300 m a 1 km [5]
| Cálculo del error porcentual en mrad |
|---|
La aproximación usando mrad es más precisa que usar otro sistema común donde 1′ ( minuto de arco ) se aproxima a 1 pulgada a 100 yardas, donde comparativamente hay:
- Error del 4,72 % al suponer que un ángulo de 1′ equivale a 1 pulgada a 100 yardas [6]
- Error del 4,75 % para 100′, es decir, suponiendo que 100′ equivale a 100 pulgadas a 100 yardas [7]
- Error del 7,36 % para 1000′, es decir, suponiendo que 1000′ equivalen a 1000 pulgadas a 100 yardas [8]
| Cálculo del error porcentual en minutos de arco |
|---|
dónde |
Ajuste de la mira

El ajuste en milirradián se utiliza comúnmente como unidad para los clics en las perillas de ajuste mecánico (torretas) de las miras de hierro y de mira telescópica tanto en los deportes de tiro militares como civiles . A los tiradores nuevos se les suele explicar el principio de las subtensiones para que comprendan que un milirradián es una medida angular. La subtensión es la cantidad física de espacio cubierto por un ángulo y varía con la distancia. Por lo tanto, la subtensión correspondiente a un mrad (ya sea en una retícula de mrad o en ajustes de mrad) varía con el alcance. Conocer las subtensiones a diferentes distancias puede ser útil para apuntar en un arma de fuego si no hay una óptica con una retícula de mrad disponible, pero implica cálculos matemáticos y, por lo tanto, no se usa mucho en aplicaciones prácticas. Las subtensiones siempre cambian con la distancia, pero un mrad (como se observa a través de una óptica) siempre es un mrad independientemente de la distancia. Por lo tanto, las tablas balísticas y las correcciones de disparo se dan en mrad, evitando así la necesidad de cálculos matemáticos.
Si una mira telescópica tiene marcas de mrad en la retícula (o hay una mira de observación con una retícula de mrad disponible), la retícula se puede utilizar para medir cuántos mrads se deben corregir en un disparo incluso sin conocer la distancia de disparo. Por ejemplo, suponiendo que un disparo preciso realizado por un tirador experimentado no alcanza el objetivo por 0,8 mrad, como se ve a través de una óptica, y la mira del arma de fuego tiene ajustes de 0,1 mrad, el tirador debe marcar 8 clics en la mira para dar en el mismo objetivo en las mismas condiciones.
Valores de clic comunes
- Ámbitos de uso general
- Gradaciones (clics) de 1/4 ′, 1/10 mrad y 1/2 ′ se utilizan en miras de uso general para caza, tiro al blanco y tiro de largo alcance a distintas distancias. Los valores de clic son lo suficientemente precisos para ajustarse para la mayoría de los tiros al blanco y lo suficientemente gruesos para mantener baja la cantidad de clics al ajustarlos.
- Ámbitos especializados
- 0,25/10 señor, 1/8 ′ y 0,5/10 Los mrad se utilizan en miras de alcance especiales para lograr una precisión extrema en rangos de objetivo fijo, como el tiro con reposapiés . Algunas miras de hierro especiales utilizadas en rifles ISSF de 10 m , 50 m y 300 metros vienen con ajustes en cualquiera de los dos .0,5/10 mrad o 0,25/10 mrad. El pequeño valor de ajuste significa que estas miras se pueden ajustar en incrementos muy pequeños. Sin embargo, estos ajustes finos no son muy adecuados para marcar entre distancias variadas, como en el tiro de campo, debido a la gran cantidad de clics que se requerirán para mover la línea de visión, lo que hace que sea más fácil perder la noción del número de clics que en visores con ajustes de clic más grandes. Por ejemplo, para mover la línea de visión 0,4 mrad, un visor de 0,1 mrad debe ajustarse 4 clics, mientras que, de manera comparable, un visor de 0,05 mrad y 0,025 mrad deben ajustarse 8 y 16 clics respectivamente.
- Otros
- 1.5/10 mrad y 2/10El mrad se puede encontrar en algunas miras de corto alcance, en su mayoría con torretas cubiertas, pero no se usa mucho.
Subtensiones a diferentes distancias

La subtensión se refiere a la longitud entre dos puntos de un objetivo y suele expresarse en centímetros, milímetros o pulgadas. Dado que un mrad es una medida angular, la subtensión cubierta por un ángulo determinado ( distancia angular o diámetro angular ) aumenta con la distancia de observación hasta el objetivo. Por ejemplo, el mismo ángulo de 0,1 mrad subtenderá 10 mm a 100 metros, 20 mm a 200 metros, etc., o de forma similar, 0,39 pulgadas a 100 m, 0,78 pulgadas a 200 m, etc.
Las subtensiones en ópticas basadas en mrad son particularmente útiles junto con los tamaños de objetivo y las distancias de disparo en unidades métricas . El incremento de ajuste de mira más común en miras de rifle basadas en mrad es 0,1 mrad, que a veces se denominan "clics de un centímetro", ya que 0,1 mrad equivale exactamente a 1 cm a 100 metros, 2 cm a 200 metros, etc. De manera similar, un clic de ajuste en una mira con un ajuste de 0,2 mrad moverá el punto de impacto de la bala 2 cm a 100 m y 4 cm a 200 m, etc.
Cuando se utiliza un visor con ajuste en mrad y una retícula con marcas en mrad (llamado visor mrad/mrad), el tirador puede detectar el impacto de su propia bala y corregir fácilmente la mira si es necesario. Si el disparo fue un error, la retícula en mrad se puede utilizar simplemente como una "regla" para contar la cantidad de milirradianes que el disparo estuvo fuera del objetivo. La cantidad de milirradianes a corregir se multiplica entonces por diez si el visor tiene ajustes de 0,1 mrad. Si, por ejemplo, el disparo fue 0,6 mrad a la derecha del objetivo, se necesitarán 6 clics para ajustar la mira. De esta manera, no hay necesidad de matemáticas, conversiones, conocimiento del tamaño del objetivo o la distancia. Esto es cierto para un visor de primer plano focal en todos los aumentos, pero un segundo plano focal variable debe configurarse a un aumento determinado (normalmente su aumento máximo) para que cualquier escala en mrad sea correcta.
Al utilizar un visor con ajustes en mrad, pero sin marcas en mrad en la retícula (es decir, una cruz dúplex estándar en un visor de caza o de banco), la corrección de la mira para una subtensión de objetivo conocida y un alcance conocido se puede calcular con la siguiente fórmula, que utiliza el hecho de que un ajuste de 1 mrad cambia el impacto tantos milímetros como metros:
Por ejemplo:
- 20 milímetros/50 metros = 0,4 mrad, o 4 clics con un 1/10Alcance de ajuste mrad .
- 50 milímetros/1000 metros = 0,05 mrad, o 1 clic con un alcance de ajuste de 0,05 mrad.
En la óptica de armas de fuego, donde 0,1 mrad por clic es el valor de ajuste basado en mrad más común, otra regla general común es que un ajuste de 1/10 mrad cambia el impacto tantos centímetros como centenas de metros. Es decir, 1 cm a 100 metros, 2,25 cm a 225 metros, 0,5 cm a 50 metros, etc. Véase la tabla siguiente
| Rango | Subtensión | |||
|---|---|---|---|---|
| 1 mrad | 1/10 señor | |||
| 100 metros | 100 milímetros | 10 centímetros | 10 milímetros | 1 centímetro |
| 200 metros | 200 milímetros | 20 centímetros | 20 milímetros | 2 centímetros |
| 300 metros | 300 milímetros | 30 centímetros | 30 milímetros | 3 centímetros |
| 400 metros | 400 milímetros | 40 centímetros | 40 milímetros | 4 centímetros |
| 500 metros | 500 milímetros | 50 centímetros | 50 milímetros | 5 centímetros |
| 600 metros | 600 milímetros | 60 centímetros | 60 milímetros | 6 centímetros |
| 700 metros | 700 milímetros | 70 centímetros | 70 milímetros | 7 centímetros |
| 800 metros | 800 milímetros | 80 centímetros | 80 milímetros | 8 centímetros |
| 900 metros | 900 milímetros | 90 centímetros | 90 milímetros | 9 centímetros |
| 1000 metros | 1000 milímetros | 100 centímetros | 100 milímetros | 10 centímetros |
Rango de ajuste e inclinación de la base

El rango de ajuste horizontal y vertical de una mira de arma de fuego suele anunciarse por el fabricante utilizando mrads. Por ejemplo, una mira telescópica para rifle puede anunciarse como que tiene un rango de ajuste vertical de 20 mrad, lo que significa que al girar la torreta, el impacto de la bala se puede mover un total de 20 metros a 1000 metros (o 2 m a 100 m, 4 m a 200 m, 6 m a 300 m, etc.). Los rangos de ajuste horizontal y vertical pueden ser diferentes para una mira en particular, por ejemplo, una mira telescópica puede tener un ajuste vertical de 20 mrad y horizontal de 10 mrad. La elevación difiere entre modelos, pero alrededor de 10-11 mrad son comunes en las miras de caza, mientras que las miras diseñadas para disparos de largo alcance generalmente tienen un rango de ajuste de 20-30 mrad (70-100 moa). [ cita requerida ]
Las miras pueden montarse en monturas neutras o inclinadas. En una montura neutra (también conocida como "base plana" o montura no inclinada) la mira apuntará razonablemente paralela al cañón y estará cerca de cero a 100 metros (aproximadamente 1 mrad menos, dependiendo del rifle y el calibre). Después de poner a cero a 100 metros, la mira siempre tendrá que ajustarse hacia arriba para compensar la caída de la bala a distancias mayores y, por lo tanto, el ajuste por debajo de cero nunca se utilizará. Esto significa que cuando se utiliza una montura neutra, solo aproximadamente la mitad de la elevación total de la mira será utilizable para disparar a distancias mayores:
En la mayoría de los rifles deportivos y de caza habituales (excepto en los de largo alcance), las miras suelen montarse en monturas neutras. Esto se hace porque la calidad óptica de la mira es mejor en la mitad de su rango de ajuste, y poder utilizar solo la mitad del rango de ajuste para compensar la caída de la bala rara vez es un problema en los disparos de corto y medio alcance.
Sin embargo, en tiro a larga distancia, los soportes de mira inclinados son comunes, ya que es muy importante tener suficiente ajuste vertical para compensar la caída de la bala a distancias más largas. Para este propósito, los soportes de mira se venden con distintos grados de inclinación, pero algunos valores comunes son:
- 3 mrad, que equivale a 3 m a 1000 m (o 0,3 m a 100 m)
- 6 mrad, que equivale a 6 m a 1000 m (o 0,6 m a 100 m)
- 9 mrad, que equivale a 9 m a 1000 m (o 0,9 m a 100 m)
Con un montaje inclinado, la elevación máxima utilizable del telescopio se puede encontrar mediante:
El rango de ajuste necesario para disparar a una determinada distancia varía según el arma de fuego, el calibre y la carga. Por ejemplo, con una determinada combinación de arma y carga de .308 , la bala puede alcanzar 13 mrad a 1000 metros (13 metros). Para poder alcanzar la distancia, se podría:
- Utilice un visor con 26 mrad de ajuste en una montura neutral para obtener un ajuste utilizable de 26 mrad/2 = 13 mrad
- Utilice un visor con un ajuste de 14 mrad y una montura inclinada de 6 mrad para lograr un ajuste máximo de 14 mrad/2+ 6 = 13 mrad
Agrupaciones de disparos
El grupo de la izquierda mide unos 13 mm y fue disparado a unos 45 metros, lo que equivale a 13 milímetros/45 metros = 0,289 mrad.
El grupo de la derecha mide unos 7 mm y fue disparado a unos 90 metros, lo que equivale a 7 milímetros/90 metros = 0,078 mrad.
Una agrupación de disparos es la distribución de varios disparos sobre un objetivo, realizados en una sesión de tiro. El tamaño del grupo sobre el objetivo en milirradianes se puede obtener midiendo la distribución de los disparos sobre el objetivo en milímetros con un calibrador y dividiéndolo por la distancia de tiro en metros. De esta manera, utilizando milirradianes, uno puede comparar fácilmente las agrupaciones de disparos o las dificultades del objetivo a diferentes distancias de tiro.
Si el arma de fuego está fijada en un soporte y apunta a un objetivo, la agrupación de disparos mide la precisión mecánica del arma de fuego y la uniformidad de la munición. Cuando el arma de fuego también está en manos de un tirador, la agrupación de disparos mide en parte la precisión del arma de fuego y la munición, y en parte la consistencia y la habilidad del tirador. A menudo, la habilidad del tirador es el elemento más importante para lograr una agrupación de disparos ajustada, [ cita requerida ] especialmente cuando los competidores utilizan las mismas armas de fuego y municiones de competición.
Estimación de alcance con retículas mrad

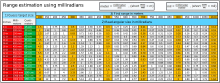
Muchas miras telescópicas que se utilizan en rifles tienen retículas marcadas en mrad. Esto se puede lograr con líneas o puntos, y estos últimos generalmente se denominan mil-dots. La retícula mrad tiene dos propósitos: estimación de alcance y corrección de trayectoria.
Con una mira equipada con retícula mrad, un usuario entrenado puede estimar la distancia a un objeto con un grado razonable de precisión al determinar cuántos miliradianes subtiende un objeto de tamaño conocido. Una vez que se conoce la distancia, la caída de la bala a esa distancia (ver balística externa ), convertida nuevamente a miliradianes, se puede utilizar para ajustar el punto de mira. Generalmente, las miras con retícula mrad tienen puntos de mira horizontales y verticales marcados; las marcas horizontales y verticales se utilizan para la estimación de la distancia y las marcas verticales para la compensación de la caída de la bala. Sin embargo, los usuarios entrenados también pueden utilizar los puntos horizontales para compensar la deriva de la bala debido al viento. Las miras equipadas con retícula milirradian son adecuadas para disparos a larga distancia en condiciones inciertas, como las que encuentran los francotiradores militares y de las fuerzas del orden , los cazadores de alimañas y otros tiradores de campo. Estos tiradores deben poder apuntar a diferentes objetivos a distancias desconocidas (a veces largas), por lo que se requiere una compensación precisa de la caída de la bala.

El ángulo se puede utilizar para calcular el tamaño del objetivo o el alcance si se conoce uno de ellos. Si se conoce el alcance, el ángulo dará el tamaño; si se conoce el tamaño, se dará el alcance. Cuando se está en el campo, el ángulo se puede medir de forma aproximada utilizando una óptica calibrada o de forma aproximada utilizando los dedos y las manos. Con el brazo extendido, un dedo tiene aproximadamente 30 mrad de ancho, un puño 150 mrad y una mano extendida 300 mrad.
Las retículas milirradianas suelen tener puntos o marcas con un espaciado de 1 mrad entre ellos, pero las graduaciones también pueden ser más finas o más gruesas (es decir, 0,8 o 1,2 mrad).
Unidades para el tamaño y el alcance del objetivo
Mientras que un radián se define como un ángulo en el círculo unitario donde el arco y el radio tienen la misma longitud, un milirradián se define como el ángulo donde la longitud del arco es una milésima parte del radio. Por lo tanto, cuando se utilizan milirradianes para la estimación de la distancia, la unidad utilizada para la distancia al objetivo debe ser mil veces más grande que la unidad utilizada para el tamaño del objetivo. Las unidades métricas son particularmente útiles junto con una retícula en mrad porque el cálculo mental es mucho más simple con unidades decimales, lo que requiere menos cálculo mental en el campo. Al utilizar la fórmula de estimación de la distancia con las unidades metros para la distancia y milímetros para el tamaño del objetivo, es solo una cuestión de mover decimales y hacer la división, sin la necesidad de multiplicar con constantes adicionales, lo que produce menos errores de redondeo.
| Derivación de la fórmula del rango |
|---|
Estas relaciones se pueden derivar fácilmente observando las unidades:
y viceversa
|
Lo mismo se aplica al cálculo de la distancia al objetivo en kilómetros utilizando el tamaño del objetivo en metros.
Además, en general, se puede utilizar la misma unidad para subtensión y rango si se multiplica por un factor de mil, es decir
Si se utilizan las unidades imperiales yardas para la distancia y pulgadas para el tamaño del objetivo, hay que multiplicar por un factor de 1000 ⁄ 36 ≈ 27,78, ya que hay 36 pulgadas en una yarda.
Si se utiliza la unidad métrica metros para la distancia y la unidad imperial pulgadas para el tamaño del objetivo, hay que multiplicar por un factor de 25,4, ya que una pulgada se define como 25,4 milímetros.
Ejemplos prácticos

Los Land Rover miden entre 3 y 4 m de largo, los "tanques pequeños" o APC / MICV miden unos 6 m (por ejemplo, el T-34 o el BMP ) y unos 10 m los "tanques grandes". De frente, un Land Rover mide alrededor de 1,5 m de ancho, la mayoría de los tanques miden entre 3 y 3,5 m. Por lo tanto, un Land Rover SWB visto de lado mide un dedo de ancho, unos 100 m. Un tanque moderno tendría que medir un poco más de 300 m.
Por ejemplo, si se mide un objetivo que se sabe que tiene una altura de 1,5 m (1500 mm) a 2,8 mrad en la retícula, el alcance se puede estimar en:
Así, si el BMP de 6 m de longitud (6000 mm) antes mencionado se observa a 6 mrad, su distancia es de 1000 m, y si el ángulo de visión es el doble (12 mrad), la distancia es la mitad, 500 m.
Cuando se utiliza con algunos visores de aumento de objetivo variable y aumento de retícula fija (donde la retícula está en el segundo plano focal), la fórmula se puede modificar a:
Donde mag es el aumento del visor. Sin embargo, el usuario debe verificar esto con su visor individual, ya que algunos no están calibrados a 10×. Como se mencionó anteriormente, la distancia y el tamaño del objetivo se pueden indicar en dos unidades de longitud con una relación de 1000:1.
Mezcla de mrad y minutos de arco
Es posible comprar visores con retícula mrad y torretas de un minuto de arco, pero existe un consenso general de que se debe evitar esa combinación. Es preferible tener tanto una retícula mrad como un ajuste mrad (mrad/mrad), o una retícula de un minuto de arco y un ajuste de un minuto de arco para aprovechar la potencia de cada sistema. De este modo, el tirador puede saber exactamente cuántos clics debe corregir en función de lo que ve en la retícula.
Si se utiliza un visor de sistema mixto que tiene una retícula de mrad y un ajuste de minutos de arco, una forma de utilizar la retícula para las correcciones de disparo es aprovechar que 14′ equivale aproximadamente a 4 mrad y, por lo tanto, multiplicar las correcciones observadas en mrad por una fracción de14/4 al ajustar las torretas.
Tabla de conversión de armas de fuego

En la siguiente tabla, las conversiones de mrad a valores métricos son exactas (por ejemplo, 0,1 mrad equivale exactamente a 1 cm a 100 metros), mientras que las conversiones de minutos de arco a valores métricos e imperiales son aproximadas.
| Incrementar o hacer clic | ( minutos de arco ) | (miliradianes) | A 100 m | A 100 yardas | ||
|---|---|---|---|---|---|---|
| ( mm ) | ( cm ) | ( en ) | ( en ) | |||
| 1 ⁄ 12 ′ | 0,083′ | 0,024 mrad | 2,42 milímetros | 0,242 cm | 0,0958 pulgadas | 0,087 pulgadas |
| 0,25 ⁄ 10 mrad | 0,086′ | 0,025 mrad | 2,5 milímetros | 0,25 centímetros | 0,0985 pulgadas | 0,09 pulgadas |
| 1 ⁄ 8 ′ | 0,125′ | 0,036 mrad | 3,64 milímetros | 0,36 centímetros | 0,144 pulgadas | 0,131 pulgadas |
| 1 ⁄ 6 ′ | 0,167′ | 0,0485 mrad | 4,85 milímetros | 0,485 centímetros | 0,192 pulgadas | 0,175 pulgadas |
| 0,5 ⁄ 10 mrad | 0,172′ | 0,05 mrad | 5 milímetros | 0,5 centímetros | 0,197 pulgadas | 0,18 pulgadas |
| 1 ⁄ 4 ′ | 0,25′ | 0,073 mrad | 7,27 milímetros | 0,73 centímetros | 0,29 pulgadas | 0,26 pulgadas |
| 1 ⁄ 10 mrad | 0,344′ | 0,1 mrad | 10 milímetros | 1 centímetro | 0,39 pulgadas | 0,36 pulgadas |
| 1 ⁄ 2 ′ | 0,5′ | 0,145 mrad | 14,54 milímetros | 1,45 centímetros | 0,57 pulgadas | 0,52 pulgadas |
| 1,5 ⁄ 10 mrad | 0,516′ | 0,15 mrad | 15 milímetros | 1,5 centímetros | 0,59 pulgadas | 0,54 pulgadas |
| 2 ⁄ 10 mrad | 0,688′ | 0,2 mrad | 20 milímetros | 2 centímetros | 0,79 pulgadas | 0,72 pulgadas |
| 1′ | 1.0′ | 0,291 mrad | 29,1 milímetros | 2,91 centímetros | 1,15 pulgadas | 1.047 pulgadas |
| 1 mrad | 3.438′ | 1 mrad | 100 milímetros | 10 centímetros | 3,9 pulgadas | 3,6 pulgadas |
- 0,1 mrad equivale exactamente a 1 cm a 100 m
- 1 mrad ≈ 3,44′, por lo que 1/10 mrad≈1/3 ′
- 1′ ≈ 0,291 mrad (o 2,91 cm a 100 m, aproximadamente 3 cm a 100 m)
Definiciones para mapas y artillería


Por la definición de pi, en un círculo con un diámetro de uno hay 2000 π milirradianes ( ≈ 6283,185 mrad ) por vuelta completa. En otras palabras, un milirradián real cubre poco menos de 1/6283 de la circunferencia de un círculo, que es la definición utilizada por los fabricantes de miras telescópicas para rifles en retículas para medición estadiamétrica de distancia . [ cita requerida ]
Para los mapas y la artillería se utilizan tres definiciones redondeadas que se aproximan a la definición real, pero que se pueden dividir en partes con mayor facilidad. Las distintas definiciones de mapas y artillería se denominan a veces "milésimas angulares" y son:
- 1/6400 de un círculo en los países de la OTAN .
- 1/6000 de un círculo en la ex Unión Soviética y Finlandia (Finlandia está eliminando gradualmente el estándar en favor del estándar de la OTAN [ cita requerida ] ).
- 1/6300 de un círculo en Suecia . El término sueco para esto es streck , que literalmente significa "línea". [a]
Las retículas de algunas miras de artillería están calibradas según la definición de artillería pertinente para ese ejército, es decir, la mira de artillería Carl Zeiss OEM-2 fabricada en Alemania del Este entre 1969 y 1976 está calibrada para el círculo de 6000 millas del bloque oriental. [ cita requerida ]
Se han utilizado varios símbolos para representar milésimas angulares para el uso de la brújula:
- mil , MIL y abreviaturas similares se utilizan a menudo en los ejércitos de la parte anglófona del mundo. [ cita requerida ]
- ‰ , llamado "artillería por mil " (en alemán: Artilleriepromille ), un símbolo utilizado por el ejército suizo . [ cita requerida ]
- ¯ , llamada "línea de artillería" (en alemán: artilleristische Strich ), un símbolo utilizado por el ejército alemán [ cita requerida ] (no debe confundirse con Compass Point (en alemán: Nautischer Strich , 32 "líneas náuticas" por círculo) que a veces utiliza el mismo símbolo. Sin embargo, la norma DIN (DIN 1301 parte 3) es utilizar ¯ para líneas de artillería y " para líneas náuticas).
- ₥ , llamado "milésimas" (en francés: millièmes ), un símbolo utilizado en algunas brújulas francesas más antiguas. [9]
- v (finlandés: piiru , sueco: delstreck ), símbolo utilizado por las Fuerzas de Defensa de Finlandia para el ejército estándar del Pacto de Varsovia. [10] A veces se marca simplemente como v si el superíndice no está disponible. [11]
Tabla de conversión de brújulas
| Miliradián | Milicia de la OTAN | Pacto de Varsovia Mil | Streck sueco | Doblar | Grados | Minuto de arco | |
|---|---|---|---|---|---|---|---|
| 1 milirradián = | 1 | 1.018 592 | 0,954 930 | 1.002 677 | 1 ⁄ 2000 π | 9/50π ≈0,057 296 | 54/5π ≈3.437 747 |
| 1 millón de la OTAN = | 0,981 719 | 1 | 0,9375 | 0,984 375 | 1 ⁄ 6400 | 0,056 25 | 3.375 |
| 1 mil del Pacto de Varsovia = | 1.047 167 | 1.066 667 | 1 | 1.05 | 1 ⁄ 6000 | 0,06 | 3.6 |
| 1 streck sueco = | 0,997 302 | 1.015 873 | 0,952 381 | 1 | 1 ⁄ 6300 | 0,057 143 | 3.428 572 |
| 1 Línea náutica = | 196.349 541 | 200 | 187,5 | 196.875 | 1 ⁄ 32 | 11.25 | 675 |
| 1 grado = | 50π/9 ≈17.452 778 | 17.777 778 | 16.666 667 | 17.5 | 1 ⁄ 360 | 1 | 60 |
| 1 minuto de arco = | 5π/54 ≈0,290 880 | 0,296 297 | 0,277 778 | 0,291 667 | 1 ⁄ 21600 | 0,016 667 | 1 |
- Una rosa de los vientos de 360 grados y 6400 millas de la OTAN.
- Brújula del ejército suizo con 6400 ‰ ("artillería por mil")
- Brújula del ejército de EE. UU. con escalas tanto de 360 grados como de 6400 millas de la OTAN.
- Brújula de muñeca del ejército soviético con dos escalas (opuestas), 360 grados en el sentido de las agujas del reloj y 6000 milésimas soviéticas en el sentido contrario a las agujas del reloj.
Uso en miras de artillería
La artillería utiliza la medición angular para apuntar el cañón, el acimut entre el cañón y su objetivo a muchos kilómetros de distancia y el ángulo de elevación del cañón. Esto significa que la artillería utiliza milésimas para graduar las miras acimutales de fuego indirecto (llamadas miras de cuadrante o telescopios panorámicos ), sus instrumentos asociados ( directores o círculos de puntería ), sus miras de elevación ( clinómetros o cuadrantes ), junto con sus dispositivos de trazado manual, tablas de tiro y computadoras de control de tiro.
Los observadores de artillería suelen utilizar sus binoculares calibrados para desplazar el impacto de los proyectiles disparados hacia un objetivo. De esta forma, conocen la distancia aproximada hasta el objetivo y pueden leer el ángulo (+ cálculo rápido) para dar las correcciones izquierda/derecha en metros. Un mil es un metro a una distancia de mil metros (por ejemplo, para desplazar el impacto de un proyectil de artillería 100 metros por un cañón que dispara desde una distancia de 3 km, es necesario cambiar la dirección en 100/3 = 33,3 milésimas).
Otros usos científicos y tecnológicos
El milirradián (y otros múltiplos del SI ) también se utiliza en otros campos de la ciencia y la tecnología para describir ángulos pequeños, es decir, medir la alineación, [12] [13] la colimación , [14] y la divergencia del haz en óptica , [15] y acelerómetros y giroscopios en sistemas de navegación inercial . [16] [17]
Véase también
- Milla escandinava , una unidad de longitud común en Noruega y Suecia , pero no en Dinamarca , hoy estandarizada a 10 kilómetros .
- Milésima de pulgada , una unidad basada en pulgadas a menudo llamada milésima o milésima de pulgada .
- Milímetro circular , unidad de área, igual al área de un círculo con un diámetro de una milésima de pulgada.
- Milésima cuadrada , unidad de área, igual al área de un cuadrado con lados de longitud de una milésima de pulgada.
Notas al pie
- ^ Suecia (y Finlandia) no han formado parte de la OTAN ni del Pacto de Varsovia . Sin embargo, Suecia ha cambiado sus sistemas de cuadrícula de mapas y de medición angular por los utilizados por la OTAN, por lo que la unidad de medida "streck" ha quedado obsoleta. [ cita requerida ]
Referencias
- ^ "Cómo utilizar telescopios ajustables en miliradianes". Outdoor Hub . 14 de julio de 2011.
- ^ Renaud, Hugues (31 de mayo de 2002). Diccionario histórico de la Suiza. Fondo, AV Laussane.
Moteados: ... Charles-Marc (1837-1920), ingeniero, profesor de la universidad de Lausana, municipal de Lausana, es el inventor de la unidad apelada "millième" para medir los ángulos en el tiro de artillería. . Una rama de la familia está fijada en genes de finales del siglo XVIII.
- ^ "Cálculo del error de aproximación para 0,1 mrad". Wolfram Alpha .
- ^ "Cálculo del error de aproximación para 30 mrad". Wolfram Alpha .
- ^ "Cálculo del error de aproximación para 300 mrad". Wolfram Alpha .
- ^ "Cálculo del error de aproximación para 1′". Wolfram Alpha .
- ^ "Cálculo del error de aproximación para 100′". Wolfram Alpha .
- ^ "Cálculo del error de aproximación para 1000′". Wolfram Alpha .
- ^ "Divisiones GB". Museo de la Brújula en línea . Compassipedia.
- ^ Taistelijan Opas 2013 (PDF) (en finlandés). Comando del Ejército (Finlandia) . ISBN 978-951-25-2485-3. Archivado (PDF) del original el 5 de mayo de 2016 . Consultado el 18 de mayo de 2019 .
- ^ "Suunnistus: Piiru" (en finlandés). Archivado desde el original el 18 de mayo de 2019. Consultado el 18 de mayo de 2019 .
- ^ "Medidor de alineación de haz óptico". Catálogo de productos opto-mecánicos . Instrumentos de medición y prueba de luz. Vilnius, LT: Standa.
- ^ "El sistema de control y alineación de espejos para CT5" (PDF) . El experimento HESS. Ginebra, CH: CERN .
- ^ "Enfoque y colimación". Newport . Nota técnica.
Soluciones fotónicas para ampliar las fronteras de la ciencia
- ^ "divergencia del haz". Enciclopedia de física y tecnología láser .
- ^ Groves, Paul D. (2013). Principios de los sistemas de navegación integrados GNSS, inerciales y multisensoriales (segunda edición). ISBN 9781608070053.
- ^ Nebylov, Alexander V.; Watson, Joseph (2016). Sistemas de navegación aeroespacial . John Wiley & Sons. ISBN 9781119163060.
Enlaces externos
- "ángulos". convertworld.com .
- Simeone, Robert J. "Mils / MOA y las ecuaciones de estimación de rango". scribd.com .
- "Compassipedia". El museo de la brújula en línea .






















