Metaheurística
Técnica de optimización

En informática y optimización matemática , una metaheurística es un procedimiento o heurística de nivel superior diseñado para encontrar, generar, ajustar o seleccionar una heurística ( algoritmo de búsqueda parcial ) que pueda proporcionar una solución suficientemente buena a un problema de optimización o un problema de aprendizaje automático , especialmente con información incompleta o imperfecta o capacidad de cálculo limitada. [1] [2] Las metaheurísticas muestrean un subconjunto de soluciones que de otro modo sería demasiado grande para ser enumerado por completo o explorado de otro modo. Las metaheurísticas pueden hacer relativamente pocas suposiciones sobre el problema de optimización que se está resolviendo y, por lo tanto, pueden ser utilizables para una variedad de problemas. [3] [4] [5] [6] Su uso siempre es de interés cuando los métodos exactos u otros (aproximados) no están disponibles o no son convenientes, ya sea porque el tiempo de cálculo es demasiado largo o porque, por ejemplo, la solución proporcionada es demasiado imprecisa.

En comparación con los algoritmos de optimización y los métodos iterativos , las metaheurísticas no garantizan que se pueda encontrar una solución globalmente óptima en alguna clase de problemas. [3] Muchas metaheurísticas implementan alguna forma de optimización estocástica , de modo que la solución encontrada depende del conjunto de variables aleatorias generadas. [2] En la optimización combinatoria , hay muchos problemas que pertenecen a la clase de problemas NP-completos y, por lo tanto, ya no se pueden resolver exactamente en un tiempo aceptable a partir de un grado de complejidad relativamente bajo. [7] [8] Las metaheurísticas a menudo proporcionan buenas soluciones con menos esfuerzo computacional que los métodos de aproximación, los métodos iterativos o las heurísticas simples. [3] [4] Esto también se aplica en el campo de la optimización continua o de números enteros mixtos. [4] [9] [10] Como tal, las metaheurísticas son enfoques útiles para los problemas de optimización. [2] Se han publicado varios libros y artículos de encuesta sobre el tema. [2] [3] [4] [11] [12] La revisión de la literatura sobre optimización metaheurística, [13] sugirió que fue Fred Glover quien acuñó la palabra metaheurística. [14]

La mayor parte de la literatura sobre metaheurísticas es de naturaleza experimental y describe resultados empíricos basados ​​en experimentos informáticos con los algoritmos. Pero también hay algunos resultados teóricos formales disponibles, a menudo sobre la convergencia y la posibilidad de encontrar el óptimo global. [3] [15] También vale la pena mencionar los teoremas de que no hay almuerzo gratis , que establecen que no puede haber ninguna metaheurística que sea mejor que todas las demás para cualquier problema dado.

Especialmente desde el cambio de milenio, se han publicado muchos métodos metaheurísticos con afirmaciones de novedad y eficacia práctica. Si bien el campo también presenta investigaciones de alta calidad, muchas de las publicaciones más recientes han sido de mala calidad; los defectos incluyen vaguedad, falta de elaboración conceptual, experimentos deficientes e ignorancia de la literatura previa. [16] [17]

Propiedades

Estas son propiedades que caracterizan la mayoría de las metaheurísticas: [3]

  • Las metaheurísticas son estrategias que guían el proceso de búsqueda.
  • El objetivo es explorar eficientemente el espacio de búsqueda para encontrar soluciones óptimas o casi óptimas.
  • Las técnicas que constituyen algoritmos metaheurísticos varían desde simples procedimientos de búsqueda local hasta procesos de aprendizaje complejos.
  • Los algoritmos metaheurísticos son aproximados y generalmente no deterministas.
  • Las metaheurísticas no son específicas de un problema, pero a menudo se desarrollaron en relación con una clase de problemas, como la optimización continua [18] [19] o la combinatoria [20], y luego se generalizaron en algunos casos. [21] [22]
  • Pueden recurrir a conocimientos específicos del dominio en forma de heurísticas que están controladas por una estrategia de nivel superior de la metaheurística.
  • Pueden contener mecanismos que eviten que se queden atascados en determinadas zonas del espacio de búsqueda.
  • Las metaheurísticas modernas a menudo utilizan el historial de búsqueda para controlar la búsqueda.

Clasificación

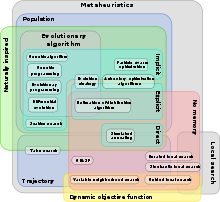
Diagrama de Euler de las diferentes clasificaciones de metaheurísticas. [23]

Existe una amplia variedad de metaheurísticas [2] [4] y un número de propiedades con respecto a las cuales clasificarlas. [3] [24] [25] [26] Por lo tanto, la siguiente lista debe entenderse como un ejemplo.

Un enfoque consiste en caracterizar el tipo de estrategia de búsqueda. [3] Un tipo de estrategia de búsqueda es una mejora de los algoritmos de búsqueda local simples. Un algoritmo de búsqueda local bien conocido es el método de escalada de colinas , que se utiliza para encontrar soluciones óptimas locales. Sin embargo, la escalada de colinas no garantiza la búsqueda de soluciones óptimas globales.

Se propusieron muchas ideas metaheurísticas para mejorar la heurística de búsqueda local con el fin de encontrar mejores soluciones. Dichas metaheurísticas incluyen el recocido simulado , la búsqueda tabú , la búsqueda local iterada , la búsqueda de vecindad variable y GRASP . [3] Estas metaheurísticas se pueden clasificar como metaheurísticas de búsqueda local o de búsqueda global.

Otras metaheurísticas de búsqueda global que no se basan en la búsqueda local suelen ser las metaheurísticas basadas en la población . Entre estas metaheurísticas se incluyen la optimización de colonias de hormigas , la computación evolutiva como el algoritmo genético o las estrategias de evolución , la optimización de enjambre de partículas , el algoritmo de optimización de jinetes [27] y el algoritmo de búsqueda de alimento bacteriano. [28]

Solución única versus basada en la población

Otra dimensión de clasificación es la búsqueda de solución única frente a la búsqueda basada en población . [3] [12] Los enfoques de solución única se centran en modificar y mejorar una única solución candidata; las metaheurísticas de solución única incluyen el recocido simulado , la búsqueda local iterada , la búsqueda de vecindad variable y la búsqueda local guiada . [12] Los enfoques basados ​​en población mantienen y mejoran múltiples soluciones candidatas, a menudo utilizando características de la población para guiar la búsqueda; las metaheurísticas basadas en población incluyen la computación evolutiva y la optimización de enjambre de partículas . [12] Otra categoría de metaheurísticas es la inteligencia de enjambre , que es un comportamiento colectivo de agentes descentralizados y autoorganizados en una población o enjambre. La optimización de colonias de hormigas , [29] la optimización de enjambre de partículas , [12] la optimización cognitiva social y el algoritmo de búsqueda de alimentos bacterianos [28] son ​​ejemplos de esta categoría.

Hibridación y algoritmos meméticos

Una metaheurística híbrida es aquella que combina una metaheurística con otros enfoques de optimización, como algoritmos de programación matemática , programación de restricciones y aprendizaje automático . Ambos componentes de una metaheurística híbrida pueden ejecutarse simultáneamente e intercambiar información para guiar la búsqueda.

Por otra parte, los algoritmos meméticos [30] representan la sinergia de un enfoque evolutivo o de cualquier enfoque basado en la población con procedimientos de aprendizaje individual o de mejora local separados para la búsqueda de problemas. Un ejemplo de algoritmo memético es el uso de un algoritmo de búsqueda local en lugar de un operador de mutación básico o además de él en algoritmos evolutivos.

Metaheurísticas paralelas

Una metaheurística paralela es aquella que utiliza las técnicas de programación paralela para ejecutar múltiples búsquedas metaheurísticas en paralelo; estas pueden variar desde esquemas distribuidos simples hasta ejecuciones de búsqueda simultáneas que interactúan para mejorar la solución general.

Con metaheurísticas basadas en la población, la población misma puede ser paralelizada ya sea procesando cada individuo o grupo con un hilo separado o la metaheurística misma se ejecuta en una computadora y la descendencia se evalúa de manera distribuida por iteración. [31] Esto último es particularmente útil si el esfuerzo computacional para la evaluación es considerablemente mayor que el de la generación de descendientes. Este es el caso en muchas aplicaciones prácticas, especialmente en cálculos basados ​​en simulación de la calidad de la solución. [32] [33]

Metaheurísticas inspiradas en la naturaleza y basadas en metáforas

Un área de investigación muy activa es el diseño de metaheurísticas inspiradas en la naturaleza. Muchas metaheurísticas recientes, especialmente algoritmos basados ​​en computación evolutiva, están inspiradas en sistemas naturales. La naturaleza actúa como una fuente de conceptos, mecanismos y principios para el diseño de sistemas informáticos artificiales para abordar problemas computacionales complejos. Dichas metaheurísticas incluyen el recocido simulado , los algoritmos evolutivos , la optimización de colonias de hormigas y la optimización de enjambres de partículas .

Un gran número de metaheurísticas más recientes inspiradas en metáforas han comenzado a atraer críticas en la comunidad de investigación por ocultar su falta de novedad detrás de una metáfora elaborada. [16] [17] [25] Como resultado, varios científicos de renombre en el campo han propuesto una agenda de investigación para la estandarización de las metaheurísticas con el fin de hacerlas más comparables, entre otras cosas. [34] Otra consecuencia es que las pautas de publicación de varias revistas científicas se han adaptado en consecuencia. [35] [36] [37]

Aplicaciones

La mayoría de las metaheurísticas son métodos de búsqueda y, al utilizarlas, la función de evaluación debe estar sujeta a mayores exigencias que una optimización matemática. No solo se debe formular el estado objetivo deseado, sino que la evaluación también debe recompensar las mejoras de una solución en el camino hacia el objetivo para apoyar y acelerar el proceso de búsqueda. Las funciones de aptitud de los algoritmos evolutivos o meméticos pueden servir como ejemplo.

Las metaheurísticas se utilizan para todo tipo de problemas de optimización, desde problemas continuos hasta problemas de números enteros mixtos, pasando por la optimización combinatoria o combinaciones de los mismos. [9] [38] [39] En la optimización combinatoria, se busca una solución óptima en un espacio de búsqueda discreto . Un ejemplo de problema es el problema del viajante , en el que el espacio de búsqueda de soluciones candidatas crece más rápido que exponencialmente a medida que aumenta el tamaño del problema, lo que hace que una búsqueda exhaustiva de la solución óptima sea inviable. [40] [41] Además, los problemas combinatorios multidimensionales, incluida la mayoría de los problemas de diseño en ingeniería [6] [42] [43] [44] como la búsqueda de formas y la búsqueda de comportamiento, sufren la maldición de la dimensionalidad , que también los hace inviables para la búsqueda exhaustiva o los métodos analíticos .

Las metaheurísticas también se aplican frecuentemente a los problemas de programación. Un representante típico de esta clase de tareas combinatorias es la programación de talleres de trabajo, que implica asignar los pasos de trabajo de los trabajos a las estaciones de procesamiento de tal manera que todos los trabajos se completen a tiempo y en conjunto en el menor tiempo posible. [5] [45] En la práctica, a menudo se deben observar restricciones, por ejemplo, limitando la secuencia permisible de pasos de trabajo de un trabajo a través de flujos de trabajo predefinidos [46] y/o con respecto a la utilización de recursos, por ejemplo, en forma de suavizado de la demanda de energía. [47] [48] Las metaheurísticas populares para problemas combinatorios incluyen algoritmos genéticos de Holland et al., [49] búsqueda dispersa [50] y búsqueda tabú [51] de Glover.

Otro gran campo de aplicación son las tareas de optimización en espacios de búsqueda de enteros continuos o mixtos. Esto incluye, por ejemplo, la optimización del diseño [6] [52] [53] o diversas tareas de ingeniería. [54] [55] [56] Un ejemplo de la mezcla de optimización combinatoria y continua es la planificación de trayectorias de movimiento favorables para robots industriales. [57] [58]

Marcos de optimización metaheurística

Un MOF puede definirse como "un conjunto de herramientas de software que proporcionan una implementación correcta y reutilizable de un conjunto de metaheurísticas, y los mecanismos básicos para acelerar la implementación de sus heurísticas subordinadas asociadas (posiblemente incluyendo codificaciones de soluciones y operadores específicos de la técnica), que son necesarias para resolver una instancia de problema particular utilizando las técnicas proporcionadas". [59]

Existen muchas herramientas de optimización candidatas que pueden considerarse MOF de características variables. La siguiente lista de 33 MOF se compara y evalúa en detalle en: [59] Comet, EvA2, evolvica, Evolutionary::Algorithm, GAPlayground, jaga, JCLEC, JGAP, jMetal, n-genes, Open Beagle, Opt4j, ParadisEO/EO, Pisa, Watchmaker, FOM, Hypercube, HotFrame, Templar, EasyLocal, iOpt, OptQuest, JDEAL, Optimization Algorithm Toolkit, HeuristicLab, MAFRA, Localizer, GALIB, DREAM, Discropt, MALLBA, MAGMA y UOF. Ha habido varias publicaciones sobre el soporte de implementaciones paralelas, que faltaba en este estudio comparativo, particularmente desde finales de los años 10 en adelante. [32] [33] [60] [61] [62]

Contribuciones

Existen muchas metaheurísticas diferentes y continuamente se proponen nuevas variantes. Algunas de las contribuciones más significativas en este campo son:

Véase también

Referencias

  1. ^ R. Balamurugan; AM Natarajan; K. Premalatha (2015). "Optimización de agujeros negros de masa estelar para datos de expresión génica de microarrays en bicluster". Inteligencia artificial aplicada . 29 (4): 353–381. doi : 10.1080/08839514.2015.1016391 . S2CID  44624424.
  2. ^ abcde Bianchi, Leonora; Marco Dorigo; Luca Maria Gambardella; Walter J. Gutjahr (2009). "Una encuesta sobre metaheurísticas para la optimización combinatoria estocástica" (PDF) . Natural Computing . 8 (2): 239–287. doi :10.1007/s11047-008-9098-4. S2CID  9141490.
  3. ^ abcdefghij Blum, Christian; Roli, Andrea (2003). "Metaheurísticas en optimización combinatoria: descripción general y comparación conceptual". Encuestas de computación de la ACM . 35 (3). ACM: 268–308. doi :10.1145/937503.937505.
  4. ^ abcde Glover, F.; Kochenberger, GA (2003). Manual de metaheurísticas . Vol. 57. Springer, International Series in Operations Research & Management Science. ISBN 978-1-4020-7263-5.
  5. ^ ab Jarboui, Bassem; Siarry, Patrick; Teghem, Jacques, eds. (2013). Metaheurísticas para la programación de la producción. Serie de ingeniería industrial, de control y automatización. Londres: ISTE. ISBN 978-1-84821-497-2.
  6. ^ abc Gupta, Shubham; Abderazek, Hammoudi; Yıldız, Betül Sultan; Yildiz, Ali Riza; Mirjalili, Seyedali; Sait, Sadiq M. (2021). "Comparación de algoritmos de optimización metaheurística para resolver problemas de optimización de diseño mecánico restringido". Sistemas expertos con aplicaciones . 183 : 115351. doi :10.1016/j.eswa.2021.115351.
  7. ^ Brucker, Peter; Knust, Sigrid (2012). Programación compleja. Berlín, Heidelberg: Springer. doi :10.1007/978-3-642-23929-8. ISBN 978-3-642-23928-1.
  8. ^ Papadimitriou, Christos H.; Steiglitz, Kenneth (1998). Optimización combinatoria: algoritmos y complejidad . Mineola, NY: Dover Publ., nueva edición corregida y completa de la obra publicada por Prentice-Hall en 1982. ISBN 978-0-486-40258-1.
  9. ^ ab Gad, Ahmed G. (2022). "Algoritmo de optimización de enjambre de partículas y sus aplicaciones: una revisión sistemática". Archivos de métodos computacionales en ingeniería . 29 (5): 2531–2561. doi : 10.1007/s11831-021-09694-4 . ISSN  1134-3060.
  10. ^ Li, Zhenhua; Lin, Xi; Zhang, Qingfu; Liu, Hailin (2020). "Estrategias evolutivas para la optimización continua: un estudio del estado del arte". Swarm and Evolutionary Computation . 56 : 100694. doi :10.1016/j.swevo.2020.100694.
  11. ^ Goldberg, DE (1989). Algoritmos genéticos en búsqueda, optimización y aprendizaje automático . Kluwer Academic Publishers. ISBN 978-0-201-15767-3.
  12. ^ abcde Talbi, EG. (2009). Metaheurísticas: del diseño a la implementación . Wiley. ISBN 978-0-470-27858-1.
  13. ^ XS Yang, Optimización metaheurística, Scholarpedia, 6(8):11472 (2011).
  14. ^ Glover, Fred (enero de 1986). "Caminos futuros para la programación entera y vínculos con la inteligencia artificial" (PDF) . Computers and Operations Research . 13 (5): 533–549. doi :10.1016/0305-0548(86)90048-1. ISSN  0305-0548.
  15. ^ Rudolph, Günter (2001). "Las mutaciones autoadaptativas pueden conducir a una convergencia prematura". IEEE Transactions on Evolutionary Computation . 5 (4): 410–414. doi :10.1109/4235.942534. hdl : 2003/5378 .
  16. ^ ab Sörensen, Kenneth (2015). "Metaheurísticas: la metáfora expuesta". International Transactions in Operational Research . 22 (1): 3–18. CiteSeerX 10.1.1.470.3422 . doi :10.1111/itor.12001. S2CID  14042315. {{cite journal}}: CS1 maint: estado de la URL ( enlace )
  17. ^ ab Brownlee, Alexander; Woodward, John R. "Por qué nos desenamoramos de los algoritmos inspirados en la naturaleza". The Conversation (sitio web) . Consultado el 30 de agosto de 2024 .
  18. ^ Schwefel, Hans-Paul (1995). Evolución y búsqueda óptima . Serie de tecnología informática de sexta generación. Nueva York: Wiley. ISBN 978-0-471-57148-3.
  19. ^ Eberhart, R.; Kennedy, J. (1995), "Un nuevo optimizador que utiliza la teoría de enjambre de partículas", Conf. Proc. MHS'95 , IEEE, págs. 39-43, doi :10.1109/MHS.1995.494215, ISBN 978-0-7803-2676-7
  20. ^ Colorni, Alberto; Dorigo, Marco; Maniezzo, Vittorio (1991), Varela, F.; Bourgine, P. (eds.), "Optimización distribuida por colonias de hormigas", Conf. Proc. de ECAL91 - Conferencia europea sobre vida artificial , Ámsterdam: Elsevier Publ., págs. 134-142, ISBN 9780262720199
  21. ^ Socha, Krzysztof; Dorigo, Marco (2008). "Optimización de colonias de hormigas para dominios continuos". Revista Europea de Investigación Operativa . 185 (3): 1155–1173. doi :10.1016/j.ejor.2006.06.046.
  22. ^ Nissen, Volker; Krause, Matthias (1994), Reusch, Bernd (ed.), "Optimización combinatoria restringida con una estrategia de evolución", Fuzzy Logik , Berlín, Heidelberg: Springer Berlin Heidelberg, págs. 33–40, doi :10.1007/978-3- 642-79386-8_5, ISBN 978-3-540-58649-4, consultado el 24 de agosto de 2024
  23. ^ Clasificación de las metaheurísticas
  24. ^ Raidl, Günther R. (2006), Almeida, Francisco; Blesa Aguilera, María J.; Blum, Christian; Moreno Vega, José Marcos (eds.), "Una visión unificada de las metaheurísticas híbridas", Hybrid Metaheuristics , Lecture Notes in Computer Science, vol. 4030, Berlín, Heidelberg: Springer Berlin Heidelberg, pp. 1–12, doi :10.1007/11890584_1, ISBN 978-3-540-46384-9, consultado el 24 de agosto de 2024
  25. ^ ab Glover, Fred; Sörensen, Kenneth (2015). "Metaheurística". Scholarpedia . 10 (4): 6532. doi : 10.4249/scholarpedia.6532 . ISSN  1941-6016.
  26. ^ Birattari, Mauro; Paquete, Luis; Stützle, Thomas; Varrentrapp, Klaus (2001). "Clasificación de metaheurísticas y diseño de experimentos para el análisis de componentes". S2CID  18347906.
  27. ^ D, Binu (2019). "RideNN: una nueva red neuronal basada en algoritmos de optimización de Rider para el diagnóstico de fallas en circuitos analógicos". IEEE Transactions on Instrumentation and Measurement . 68 (1): 2–26. Bibcode :2019ITIM...68....2B. doi :10.1109/TIM.2018.2836058. S2CID  54459927.
  28. ^ ab Pang, Shinsiong; Chen, Mu-Chen (1 de junio de 2023). "Optimizar la programación de la tripulación ferroviaria mediante el uso de un algoritmo de búsqueda de alimentos bacterianos modificado". Computers & Industrial Engineering . 180 : 109218. doi :10.1016/j.cie.2023.109218. ISSN  0360-8352. S2CID  257990456.
  29. ^ ab M. Dorigo, Optimización, aprendizaje y algoritmos naturales , tesis doctoral, Politecnico di Milano, Italia, 1992.
  30. ^ ab Moscato, P. (1989). "Sobre evolución, búsqueda, optimización, algoritmos genéticos y artes marciales: hacia algoritmos meméticos". Programa de computación concurrente de Caltech (informe 826).
  31. ^ Cantú-Paz, Erick (2001). Algoritmos genéticos paralelos eficientes y precisos. Algoritmos genéticos y computación evolutiva. Vol. 1. Boston, MA: Springer US. doi :10.1007/978-1-4615-4369-5. ISBN 978-1-4613-6964-6.
  32. ^ de Sudholt, Dirk (2015), Kacprzyk, Janusz; Pedrycz, Witold (eds.), "Algoritmos evolutivos paralelos", Springer Handbook of Computational Intelligence , Berlín, Heidelberg: Springer, págs. 929–959, doi :10.1007/978-3-662-43505-2_46, ISBN 978-3-662-43504-5, consultado el 4 de septiembre de 2024
  33. ^ ab Khalloof, Hatem; Mohammad, Mohammad; Shahoud, Shadi; Duepmeier, Clemens; Hagenmeyer, Veit (2020-11-02), "Un marco genérico flexible y escalable para la paralelización jerárquica de metaheurísticas basadas en la población", Proc. de la 12.ª Conferencia Internacional sobre Gestión de Ecosistemas Digitales (MEDES'20) , ACM, págs. 124-131, doi :10.1145/3415958.3433041, ISBN 978-1-4503-8115-4
  34. ^ Cisne, Jerry; Adriaensen, Steven; Bishr, Mohamed; Burke, Edmund K.; Clark, Juan A.; De Causmaecke, Patrick; Durillo, Juan José; Hammond, Kevin; Hart, Emma; Johnson, Colin G.; Kocsis, Zoltan A.; Kovitz, Ben; Krawiec, Krzysztof; Martín, Simón; Merelo, Juan J.; Minku, Leandro L.; Özcan, Ender; Pappa, Gisele Lobo; Pesch, Erwin; García-Sánchez, Pablo; Schärf, Andrea; Sim, Kevin; Smith, Jim; Stützle, Thomas; Wagner, Stefan (2015). "Una agenda de investigación para la estandarización metaheurística". Académico semántico . Consultado el 30 de agosto de 2024 .
  35. ^ "Revista de políticas heurísticas sobre investigación de búsqueda heurística" (PDF) . Revista de heurística - Pautas de envío . Archivado desde el original el 2017-07-09 . Consultado el 2024-09-01 .
  36. ^ "Objetivos y alcance". 4OR . Consultado el 1 de septiembre de 2024 .
  37. ^ "Objetivos y alcance". Computación memética . Consultado el 1 de septiembre de 2024 .
  38. ^ Almeida, Francisco; Blesa Aguilera, María J.; Blum, cristiano; Moreno Vega, José Marcos; Pérez Pérez, Melquíades; Roli, Andrea; Sampels, Michael, eds. (2006). Metaheurísticas híbridas. Apuntes de conferencias sobre informática. vol. 4030. Berlín, Heidelberg: Springer. doi :10.1007/11890584. ISBN 978-3-540-46384-9.
  39. ^ Neri, Ferrante; Cotta, Carlos; Moscato, Pablo, eds. (2012). Handbook of Memetic Algorithms. Studies in Computational Intelligence. Vol. 379. Berlín, Heidelberg: Springer Berlin Heidelberg. doi :10.1007/978-3-642-23247-3. ISBN 978-3-642-23246-6.
  40. ^ Dorigo, M.; Gambardella, LM (abril de 1997). "Sistema de colonias de hormigas: un enfoque de aprendizaje cooperativo para el problema del viajante de comercio". IEEE Transactions on Evolutionary Computation . 1 (1): 53–66. doi :10.1109/4235.585892.
  41. ^ Merz, Peter; Freisleben, Bernd (2002). "Algoritmos meméticos para el problema del viajante". Sistemas complejos . 13 (4).
  42. ^ Tomoiagă B, Chindriş M, Sumper A, Sudria-Andreu A, Villafafila-Robles R. Reconfiguración óptima de Pareto de sistemas de distribución de energía utilizando un algoritmo genético basado en NSGA-II. Energías. 2013; 6(3):1439–1455.
  43. ^ Ganesan, T.; Elamvazuthi, I.; Ku Shaari, Ku Zilati; Vasant, P. (1 de marzo de 2013). "Inteligencia de enjambre y algoritmo de búsqueda gravitacional para la optimización multiobjetivo de la producción de gas de síntesis". Applied Energy . 103 : 368–374. Bibcode :2013ApEn..103..368G. doi :10.1016/j.apenergy.2012.09.059.
  44. ^ Ganesan, T.; Elamvazuthi, I.; Vasant, P. (1 de noviembre de 2011). "Método evolutivo de intersección normal-límite (ENBI) para la optimización multiobjetivo del sistema de moldes de arena verde". 2011 IEEE International Conference on Control System, Computing and Engineering . págs. 86–91. doi :10.1109/ICCSCE.2011.6190501. ISBN 978-1-4577-1642-3.S2CID698459  .​
  45. ^ Xhafa, Fatos; Abraham, Ajith, eds. (2008). Metaheurísticas para la programación en aplicaciones industriales y de fabricación. Estudios en inteligencia computacional. Vol. 128. Berlín, Heidelberg: Springer Berlin Heidelberg. doi :10.1007/978-3-540-78985-7. ISBN 978-3-540-78984-0. Número de identificación del sujeto  42238720.
  46. ^ Jakob, Wilfried; Strack, Sylvia; Quinte, Alexander; Bengel, Günther; Stucky, Karl-Uwe; Süß, Wolfgang (22 de abril de 2013). "Reprogramación rápida de múltiples flujos de trabajo para recursos heterogéneos restringidos mediante computación memética de múltiples criterios". Algorithms . 6 (2): 245–277. doi : 10.3390/a6020245 . ISSN  1999-4893.
  47. ^ Kizilay, Damla; Tasgetiren, M. Fatih; Pan, Quan-Ke; Süer, Gürsel (2019). "Un conjunto de metaheurísticas para el problema de programación de flujo de trabajo con bloqueo de eficiencia energética". Procedia Manufacturing . 39 : 1177–1184. doi : 10.1016/j.promfg.2020.01.352 . S2CID  213710393.
  48. ^ Grosch, Benedikt; Weitzel, Timm; Panten, Niklas; Abele, Eberhard (2019). "Una metaheurística para la programación de la producción adaptativa de energía con múltiples portadores de energía y su implementación en un sistema de producción real". Procedia CIRP . 80 : 203–208. doi : 10.1016/j.procir.2019.01.043 . S2CID  164850023.
  49. ^ ab Holland, JH (1975). Adaptación en sistemas naturales y artificiales . University of Michigan Press. ISBN 978-0-262-08213-6.
  50. ^ ab Glover, Fred (1977). "Heurísticas para programación de enteros usando restricciones sustitutas". Decision Sciences . 8 (1): 156–166. CiteSeerX 10.1.1.302.4071 . doi :10.1111/j.1540-5915.1977.tb01074.x. 
  51. ^ ab Glover, F. (1986). "Caminos futuros para la programación entera y vínculos con la inteligencia artificial". Computers and Operations Research . 13 (5): 533–549. doi :10.1016/0305-0548(86)90048-1.
  52. ^ Quinte, Alexander; Jakob, Wilfried; Scherer, Klaus-Peter; Eggert, Horst (2002), Laudon, Matthew (ed.), "Optimización de una placa de microactuador utilizando algoritmos evolutivos y simulación basada en métodos de elementos discretos", Conferencia internacional sobre modelado y simulación de microsistemas: MSM 2002 , Cambridge, Mass: Computational Publications, págs. 192-197, ISBN 978-0-9708275-7-9
  53. ^ Parmee, IC (1997), Dasgupta, Dipankar; Michalewicz, Zbigniew (eds.), "Estrategias para la integración de la búsqueda evolutiva/adaptativa con el proceso de diseño de ingeniería", Algoritmos evolutivos en aplicaciones de ingeniería , Berlín, Heidelberg: Springer, págs. 453–477, doi :10.1007/978-3-662-03423-1_25, ISBN 978-3-642-08282-5, consultado el 17 de julio de 2023
  54. ^ Valadi, Jayaraman; Siarry, Patrick, eds. (2014). Aplicaciones de metaheurísticas en ingeniería de procesos. Cham: Springer International Publishing. doi :10.1007/978-3-319-06508-3. ISBN 978-3-319-06507-6.S2CID40197553  .​
  55. ^ Sanchez, Ernesto; Squillero, Giovanni; Tonda, Alberto (2012). Aplicaciones industriales de algoritmos evolutivos. Biblioteca de referencia de sistemas inteligentes. Vol. 34. Berlín, Heidelberg: Springer. doi :10.1007/978-3-642-27467-1. ISBN 978-3-642-27466-4.
  56. ^ Akan, Taymaz; Anter, Ahmed M.; Etaner-Uyar, A. Şima; Oliva, Diego, eds. (2023). Aplicaciones de ingeniería de metaheurísticas modernas. Estudios en inteligencia computacional. Vol. 1069. Cham: Springer International Publishing. doi :10.1007/978-3-031-16832-1. ISBN 978-3-031-16831-4. Número de identificación S2C:  254222401.
  57. ^ Blume, Christian (2000), Cagnoni, Stefano (ed.), "Generación optimizada de instrucciones de movimiento de robots sin colisiones mediante el software evolutivo GLEAM", Aplicaciones en el mundo real de la computación evolutiva , Lecture Notes in Computer Science, vol. 1803, Berlín, Heidelberg: Springer, págs. 330–341, doi :10.1007/3-540-45561-2_32, ISBN 978-3-540-67353-8, consultado el 17 de julio de 2023
  58. ^ Pholdee, Nantiwat; Bureerat, Sujin (14 de diciembre de 2018), "Planificación de trayectoria multiobjetivo de un robot 6D basado en búsqueda heurística meta multiobjetivo", Conferencia internacional sobre redes, comunicaciones y computación (ICNCC 2018) , ACM, págs. 352–356, doi :10.1145/3301326.3301356, ISBN 978-1-4503-6553-6, Número de identificación del sujeto  77394395
  59. ^ ab Parejo, José Antonio; Ruiz-Cortés, Antonio; Lozano, Sebastián; Fernández, Pablo (marzo de 2012). "Marcos de optimización metaheurística: una encuesta y evaluación comparativa". Computación blanda . 16 (3): 527–561. doi :10.1007/s00500-011-0754-8. ISSN  1432-7643.
  60. ^ García-Valdez, Mario; Merelo, JJ (15 de julio de 2017), "evospace-js: ejecución asincrónica basada en pools de metaheurísticas heterogéneas", GECCO '17: Proceedings of the Genetic and Evolutionary Computation Conference, Companion , Nueva York: ACM, pp. 1202–1208, doi :10.1145/3067695.3082473, ISBN 978-1-4503-4939-0
  61. ^ Lim, Dudy; Ong, Yew-Soon; Jin, Yaochu; Sendhoff, Bernhard; Lee, Bu-Sung (mayo de 2007). "Algoritmos genéticos paralelos jerárquicos eficientes utilizando computación en cuadrícula". Future Generation Computer Systems . 23 (4): 658–670. doi :10.1016/j.future.2006.10.008.
  62. ^ Nebro, Antonio J.; Barba-González, Cristóbal; Nieto, José García; Cordero, José A.; Montes, José F. Aldana (15 de julio de 2017), "Diseño y arquitectura del marco jMetaISP", GECCO '17: Actas de la Conferencia sobre Computación Genética y Evolutiva, Companion , Nueva York: ACM, págs. doi :10.1145/3067695.3082466, ISBN 978-1-4503-4939-0
  63. ^ Robbins, H.; Monro, S. (1951). "Un método de aproximación estocástica" (PDF) . Anales de estadística matemática . 22 (3): 400–407. doi : 10.1214/aoms/1177729586 .
  64. ^ Barricelli, NA (1954). "Ejemplos numéricos de procesos de evolución". Métodos : 45–68.
  65. ^ Rastrigin, LA (1963). "La convergencia del método de búsqueda aleatoria en el control extremo de un sistema de muchos parámetros". Automatización y control remoto . 24 (10): 1337–1342.
  66. ^ Matyas, J. (1965). "Optimización aleatoria". Automatización y control remoto . 26 (2): 246–253.
  67. ^ Nelder, JA; Mead, R. (1965). "Un método simplex para la minimización de funciones". Revista informática . 7 (4): 308–313. doi :10.1093/comjnl/7.4.308. S2CID  2208295.
  68. ^ Rechenberg, Ingo (1965). "Ruta de solución cibernética de un problema experimental". Traducción de la biblioteca del Royal Aircraft Establishment .
  69. ^ Fogel, L.; Owens, AJ; Walsh, MJ (1966). Inteligencia artificial mediante evolución simulada . Wiley. ISBN 978-0-471-26516-0.
  70. ^ Hastings, WK (1970). "Métodos de muestreo de Monte Carlo utilizando cadenas de Markov y sus aplicaciones". Biometrika . 57 (1): 97–109. Bibcode :1970Bimka..57...97H. doi :10.1093/biomet/57.1.97. S2CID  21204149.
  71. ^ Cavicchio, DJ (1970). "Búsqueda adaptativa mediante evolución simulada". Informe técnico . Universidad de Michigan, Departamento de Ciencias de la Computación y la Comunicación. hdl :2027.42/4042.
  72. ^ Kernighan, BW; Lin, S. (1970). "Un procedimiento heurístico eficiente para particionar grafos". Bell System Technical Journal . 49 (2): 291–307. doi :10.1002/j.1538-7305.1970.tb01770.x.
  73. ^ Mercer, RE; Sampson, JR (1978). "Búsqueda adaptativa utilizando un metaplan reproductivo". Kybernetes . 7 (3): 215–228. doi :10.1108/eb005486.
  74. ^ Smith, SF (1980). Un sistema de aprendizaje basado en algoritmos adaptativos genéticos (tesis doctoral). Universidad de Pittsburgh.
  75. ^ Kirkpatrick, S.; Gelatt Jr., CD; Vecchi, MP (1983). "Optimización mediante recocido simulado". Science . 220 (4598): 671–680. Bibcode :1983Sci...220..671K. CiteSeerX 10.1.1.123.7607 . doi :10.1126/science.220.4598.671. PMID  17813860. S2CID  205939. 
  76. ^ Moscato, P.; Fontanari, JF (1990), "Actualización estocástica versus determinista en recocido simulado", Physics Letters A , 146 (4): 204–208, Bibcode :1990PhLA..146..204M, doi :10.1016/0375-9601(90)90166-L
  77. ^ Dueck, G.; Scheuer, T. (1990), "Aceptación de umbral: Un algoritmo de optimización de propósito general que parece superior al recocido simulado", Journal of Computational Physics , 90 (1): 161–175, Bibcode :1990JCoPh..90..161D, doi :10.1016/0021-9991(90)90201-B, ISSN  0021-9991
  78. ^ Wolpert, DH; Macready, WG (1995). "No hay teoremas gratuitos para la búsqueda". Informe técnico SFI-TR-95-02-010 . Instituto Santa Fe. S2CID  12890367.
  79. ^ Igel, Christian, Toussaint, Marc (junio de 2003). "Sobre clases de funciones para las que se cumplen los resultados de No Free Lunch". Information Processing Letters . 86 (6): 317–321. arXiv : cs/0108011 . doi :10.1016/S0020-0190(03)00222-9. ISSN  0020-0190. S2CID  147624.{{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )
  80. ^ Auger, Anne , Teytaud, Olivier (2010). "Los almuerzos continuos son gratis más el diseño de algoritmos de optimización óptimos". Algorithmica . 57 (1): 121–146. CiteSeerX 10.1.1.186.6007 . doi :10.1007/s00453-008-9244-5. ISSN  0178-4617. S2CID  1989533. {{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )
  81. ^ Stefan Droste; Thomas Jansen; Ingo Wegener (2002). "Optimización con heurísticas de búsqueda aleatorias: el teorema (A)NFL, escenarios realistas y funciones difíciles". Ciencias de la computación teórica . 287 (1): 131–144. CiteSeerX 10.1.1.35.5850 . doi :10.1016/s0304-3975(02)00094-4. 

Lectura adicional

  • Sörensen, Kenneth; Sevaux, Marc; Glover, Fred (16 de enero de 2017). "Una historia de las metaheurísticas" (PDF) . En Martí, Rafael; Panos, Párdalos; Resende, Mauricio (eds.). Manual de heurística . Saltador. ISBN 978-3-319-07123-7.
  • Ashish Sharma (2022), Algoritmos inspirados en la naturaleza con perspectiva hipercomputacional aleatoria. Ciencias de la información. https://doi.org/10.1016/j.ins.2022.05.020.
  • Fred Glover y Kenneth Sörensen (ed.). "Metaheurística". Scholarpedia .
  • Foro UE/ME para investigadores en este campo.
  • Metaheuristics.jl Fuente de algunas implementaciones.
Obtenido de "https://es.wikipedia.org/w/index.php?title=Metaheurística&oldid=1244797749"