Correa electrodinámica

Las ataduras electrodinámicas ( EDT ) son cables conductores largos , como uno desplegado desde un satélite de amarre, que pueden funcionar según principios electromagnéticos como generadores , convirtiendo su energía cinética en energía eléctrica , o como motores , convirtiendo la energía eléctrica en energía cinética. [1] El potencial eléctrico se genera a través de una atadura conductora por su movimiento a través del campo magnético de un planeta.
Varias misiones han demostrado la existencia de ataduras electrodinámicas en el espacio, entre las que destacan los experimentos TSS-1 , TSS-1R y Plasma Motor Generator (PMG).
Propulsión por amarre
Como parte de un sistema de propulsión por amarre , las naves pueden utilizar conductores largos y resistentes (aunque no todos los amarres son conductores) para cambiar las órbitas de las naves espaciales . Tiene el potencial de hacer que los viajes espaciales sean significativamente más baratos. [ cita requerida ] Cuando se aplica corriente continua al amarre, ejerce una fuerza de Lorentz contra el campo magnético y el amarre ejerce una fuerza sobre el vehículo. Puede usarse para acelerar o frenar una nave espacial en órbita.
En 2012, Star Technology and Research recibió un contrato de 1,9 millones de dólares para calificar un sistema de propulsión por cable para la eliminación de desechos orbitales . [2]
Usos de los anclajes para disfunción eréctil
Esta sección está escrita como una reflexión personal, un ensayo personal o un ensayo argumentativo que expresa los sentimientos personales de un editor de Wikipedia o presenta un argumento original sobre un tema. ( Enero de 2014 ) |
A lo largo de los años, se han identificado numerosas aplicaciones para los anclajes electrodinámicos que podrían utilizarse en la industria, el gobierno y la exploración científica. La siguiente tabla es un resumen de algunas de las posibles aplicaciones propuestas hasta el momento. Algunas de estas aplicaciones son conceptos generales, mientras que otras son sistemas bien definidos. Muchos de estos conceptos se superponen con otras áreas; sin embargo, simplemente se colocan bajo el encabezado más apropiado para los fines de esta tabla. Todas las aplicaciones mencionadas en la tabla se desarrollan en el Manual de anclajes. [1] Tres conceptos fundamentales que poseen los anclajes son los gradientes de gravedad, el intercambio de momento y la electrodinámica. Las posibles aplicaciones de los anclajes se pueden ver a continuación:
| ELECTRODINÁMICA | |
|---|---|
| Generación de energía electrodinámica | Generación de empuje electrodinámico |
| Antena de comunicación ULF/ELF/VLF | Remediación del cinturón de radiación |
| ESTACIÓN ESPACIAL | |
| Laboratorio de microgravedad | El transbordador sale de la órbita de la Estación Espacial |
| Lanzamiento del vehículo de transferencia espacial atado (STV) | Laboratorio de gravedad variable/baja |
| Estabilización y control de la actitud | Reactivación de la ISS |
| TRANSPORTE | |
| Etapas gastadas de recuperación de momento generalizado | Fuerzas internas para la modificación orbital |
| Impulso satelital desde el orbitador | Sistema de transporte asistido por correa (TATS) |
| Reactivación de satélites en descomposición mediante Tether | Impulso de la etapa superior desde el Orbitador |
Reactivación de la ISS
Se ha propuesto que la EDT mantenga la órbita de la ISS y ahorre el gasto de reimpulsos con propulsores químicos. [3] Podría mejorar la calidad y duración de las condiciones de microgravedad. [3]
Fundamentos de la atadura electrodinámica

La elección del conductor metálico que se utilizará en una atadura electrodinámica está determinada por diversos factores. Los factores principales suelen incluir una alta conductividad eléctrica y una baja densidad . Los factores secundarios, según la aplicación, incluyen el coste, la resistencia y el punto de fusión.
Se genera una fuerza electromotriz (FEM) a través de un elemento de sujeción a medida que se mueve en relación con un campo magnético. La fuerza viene dada por la Ley de inducción de Faraday :
Sin perder generalidad, se supone que el sistema de anclaje está en órbita terrestre y se mueve en relación con el campo magnético de la Tierra. De manera similar, si fluye corriente en el elemento de anclaje, se puede generar una fuerza de acuerdo con la ecuación de fuerza de Lorentz.
En el modo de autoalimentación ( modo de desorbitación ), el sistema de anclaje puede utilizar este EMF para impulsar la corriente a través del anclaje y otras cargas eléctricas (por ejemplo, resistencias, baterías), emitir electrones en el extremo emisor o recolectar electrones en el extremo opuesto. En el modo de refuerzo, las fuentes de alimentación incorporadas deben superar este EMF de movimiento para impulsar la corriente en la dirección opuesta, creando así una fuerza en la dirección opuesta, como se ve en la figura siguiente, y potenciando el sistema.
Tomemos, por ejemplo, la misión del Sistema de Despliegue de Dispositivos Pequeños de Propulsión (ProSEDS) de la NASA, como se ve en la figura anterior. [4] [5] [6] [7] [8] A 300 km de altitud, el campo magnético de la Tierra, en dirección norte-sur, es de aproximadamente 0,18-0,32 gauss hasta una inclinación de ~40°, y la velocidad orbital con respecto al plasma local es de unos 7500 m/s. Esto da como resultado un rango de fem V de 35-250 V/km a lo largo de los 5 km de longitud de la atadura. Este fem dicta la diferencia de potencial a través de la atadura desnuda que controla dónde se recogen y/o repelen los electrones. Aquí, el sistema de atadura de despotenciación ProSEDS está configurado para permitir la recogida de electrones en la sección de mayor altitud con polarización positiva de la atadura desnuda, y su retorno a la ionosfera en el extremo de menor altitud. Este flujo de electrones a lo largo de la atadura en presencia del campo magnético de la Tierra crea una fuerza que produce un empuje de arrastre que ayuda a desorbitar el sistema, como se indica en la ecuación anterior. El modo de refuerzo es similar al modo de desorbitación, excepto por el hecho de que también se inserta una fuente de alimentación de alto voltaje (HVPS) en serie con el sistema de atadura entre la atadura y el extremo de mayor potencial positivo. El voltaje de la fuente de alimentación debe ser mayor que el EMF y el polo opuesto. Esto impulsa la corriente en la dirección opuesta, lo que a su vez hace que el extremo de mayor altitud esté cargado negativamente, mientras que el extremo de menor altitud está cargado positivamente (suponiendo una órbita estándar de este a oeste alrededor de la Tierra).
Para enfatizar aún más el fenómeno de desamplificación, en la siguiente figura se puede ver un esquema de un sistema de conexión desnudo sin aislamiento (totalmente desnudo).

La parte superior del diagrama, el punto A , representa el extremo de recolección de electrones. La parte inferior de la atadura, el punto C , es el extremo de emisión de electrones. De manera similar, y representan la diferencia de potencial desde sus respectivos extremos de la atadura hasta el plasma, y es el potencial en cualquier lugar a lo largo de la atadura con respecto al plasma. Finalmente, el punto B es el punto en el que el potencial de la atadura es igual al plasma. La ubicación del punto B variará dependiendo del estado de equilibrio de la atadura, que está determinado por la solución de la ley de voltaje de Kirchhoff (KVL).
y la ley de corriente de Kirchhoff (LCK)
a lo largo de la atadura. Aquí , , y describen la ganancia de corriente del punto A al B , la corriente perdida del punto B al C y la corriente perdida en el punto C , respectivamente.
Como la corriente cambia continuamente a lo largo de la longitud desnuda de la atadura, la pérdida de potencial debido a la naturaleza resistiva del cable se representa como . A lo largo de una sección infinitesimal de la atadura, la resistencia multiplicada por la corriente que viaja a través de esa sección es la pérdida de potencial resistiva.
Después de evaluar la LVK y la LVK para el sistema, los resultados producirán un perfil de corriente y potencial a lo largo de la atadura, como se ve en la figura anterior. Este diagrama muestra que, desde el punto A de la atadura hasta el punto B , hay un sesgo de potencial positivo, que aumenta la corriente recolectada. Por debajo de ese punto, se vuelve negativo y comienza la recolección de corriente iónica. Dado que se necesita una diferencia de potencial mucho mayor para recolectar una cantidad equivalente de corriente iónica (para un área determinada), la corriente total en la atadura se reduce en una cantidad menor. Luego, en el punto C , la corriente restante en el sistema se extrae a través de la carga resistiva ( ), y se emite desde un dispositivo emisor de electrones ( ), y finalmente a través de la vaina de plasma ( ). El bucle de voltaje de la LVK se cierra entonces en la ionosfera, donde la diferencia de potencial es efectivamente cero.
Debido a la naturaleza de los EDT desnudos, a menudo no es opcional tener todo el anclaje desnudo. Para maximizar la capacidad de empuje del sistema, se debe aislar una parte significativa del anclaje desnudo. Esta cantidad de aislamiento depende de una serie de efectos, algunos de los cuales son la densidad del plasma, la longitud y el ancho del anclaje, la velocidad de órbita y la densidad del flujo magnético de la Tierra.
Las correas como generadores

Un cable electrodinámico se fija a un objeto, y el cable se orienta en un ángulo con respecto a la vertical local entre el objeto y un planeta con un campo magnético. El extremo más alejado del cable se puede dejar desnudo, lo que hace contacto eléctrico con la ionosfera . Cuando el cable intersecta el campo magnético del planeta , genera una corriente y, por lo tanto, convierte parte de la energía cinética del cuerpo en órbita en energía eléctrica. Funcionalmente, los electrones fluyen desde el plasma espacial hacia el cable conductor, pasan a través de una carga resistiva en una unidad de control y son emitidos al plasma espacial por un emisor de electrones como electrones libres. Como resultado de este proceso, una fuerza electrodinámica actúa sobre el cable y el objeto conectado, lo que ralentiza su movimiento orbital. En un sentido amplio, el proceso se puede comparar con un molino de viento convencional: la fuerza de arrastre de un medio resistivo (aire o, en este caso, la magnetosfera) se utiliza para convertir la energía cinética del movimiento relativo (viento o el momento del satélite) en electricidad. En principio, son posibles generadores de energía de alta corriente compactos y, con hardware básico, parece que se pueden lograr decenas, cientos y miles de kilovatios. [10]
Voltaje y corriente
La NASA ha llevado a cabo varios experimentos con cables de generador de plasma (PMG) en el espacio. Uno de los primeros experimentos utilizó un cable conductor de 500 metros. En 1996, la NASA llevó a cabo un experimento con un cable conductor de 20.000 metros. Cuando el cable se desplegó por completo durante esta prueba, el cable en órbita generó un potencial de 3.500 voltios. Este cable conductor de una sola línea se rompió después de cinco horas de despliegue. Se cree que la falla fue causada por un arco eléctrico generado por el movimiento del cable conductor a través del campo magnético de la Tierra. [11]
Cuando una cuerda se mueve a una velocidad ( v ) en ángulo recto con el campo magnético de la Tierra ( B ), se observa un campo eléctrico en el marco de referencia de la cuerda. Esto se puede expresar como:
- E = v * B = v B
La dirección del campo eléctrico ( E ) forma un ángulo recto con la velocidad ( v ) y el campo magnético ( B ) de la atadura. Si la atadura es un conductor, el campo eléctrico provoca el desplazamiento de cargas a lo largo de la atadura. Nótese que la velocidad utilizada en esta ecuación es la velocidad orbital de la atadura. La velocidad de rotación de la Tierra, o de su núcleo, no es relevante. A este respecto, véase también generador homopolar .
Voltaje a través del conductor
Con un cable conductor largo de longitud L se genera un campo eléctrico E en el cable, que produce un voltaje V entre los extremos opuestos del cable. Esto se puede expresar como:
- [12]
donde el ángulo τ está entre el vector de longitud ( L ) de la correa y el vector de campo eléctrico ( E ), que se supone que está en dirección vertical en ángulo recto con el vector de velocidad ( v ) en el plano y el vector de campo magnético ( B ) está fuera del plano.
Corriente en el conductor
Un cable electrodinámico puede describirse como un tipo de "sistema abierto" termodinámicamente . Los circuitos de cables electrodinámicos no pueden completarse simplemente utilizando otro cable, ya que otro cable desarrollará un voltaje similar. Afortunadamente, la magnetosfera de la Tierra no está "vacía" y, en las regiones cercanas a la Tierra (especialmente cerca de la atmósfera terrestre) existen plasmas altamente conductores de electricidad que se mantienen parcialmente ionizados por la radiación solar u otra energía radiante . La densidad de electrones e iones varía según varios factores, como la ubicación, la altitud, la estación, el ciclo de manchas solares y los niveles de contaminación. Se sabe que un conductor desnudo con carga positiva puede extraer fácilmente electrones libres del plasma. Por lo tanto, para completar el circuito eléctrico, se necesita un área suficientemente grande de conductor sin aislamiento en el extremo superior, con carga positiva, del cable, lo que permite que la corriente fluya a través del cable.
Sin embargo, es más difícil para el extremo opuesto (negativo) de la atadura expulsar electrones libres o recoger iones positivos del plasma. Es plausible que, al utilizar un área de recolección muy grande en un extremo de la atadura, se puedan recolectar suficientes iones para permitir una corriente significativa a través del plasma. Esto se demostró durante la misión TSS-1R del orbitador Shuttle, cuando el propio transbordador se utilizó como un gran contactor de plasma para proporcionar más de un amperio de corriente. Los métodos mejorados incluyen la creación de un emisor de electrones, como un cátodo termoiónico , un cátodo de plasma, un contactor de plasma o un dispositivo de emisión de electrones de campo . Dado que ambos extremos de la atadura están "abiertos" al plasma circundante, los electrones pueden fluir hacia afuera de un extremo de la atadura mientras que un flujo correspondiente de electrones ingresa al otro extremo. De esta manera, el voltaje que se induce electromagnéticamente dentro de la atadura puede hacer que la corriente fluya a través del entorno espacial circundante , completando un circuito eléctrico a través de lo que parece ser, a primera vista, un circuito abierto .
Corriente de amarre
La cantidad de corriente ( I ) que fluye a través de un cable depende de varios factores. Uno de ellos es la resistencia total del circuito ( R ). La resistencia del circuito consta de tres componentes:
- la resistencia efectiva del plasma,
- la resistencia de la atadura, y
- una resistencia variable de control.
Además, se necesita una carga parásita . La carga de la corriente puede adoptar la forma de un dispositivo de carga que, a su vez, carga fuentes de energía de reserva, como baterías. Las baterías, a su vez, se utilizarán para controlar los circuitos de energía y comunicación, así como para accionar los dispositivos emisores de electrones en el extremo negativo de la atadura. De este modo, la atadura puede autoalimentarse por completo, además de la carga inicial en las baterías para proporcionar energía eléctrica para el procedimiento de despliegue y puesta en marcha.
La carga de la batería en carga puede considerarse como una resistencia que absorbe energía, pero la almacena para su uso posterior (en lugar de disipar el calor inmediatamente). Se incluye como parte de la "resistencia de control". Sin embargo, la carga de la batería en carga no se considera una "resistencia de base", ya que el circuito de carga se puede apagar en cualquier momento. Cuando está apagado, las operaciones pueden continuar sin interrupción utilizando la energía almacenada en las baterías.
Captación/emisión de corriente para un sistema EDT: teoría y tecnología
Comprender la recolección de corriente de electrones e iones hacia y desde el plasma ambiental circundante es fundamental para la mayoría de los sistemas EDT. Cualquier sección conductora expuesta del sistema EDT puede recolectar corriente de electrones o iones de manera pasiva (la emisión "pasiva" y "activa" se refiere al uso de energía almacenada previamente para lograr el efecto deseado), dependiendo del potencial eléctrico del cuerpo de la nave espacial con respecto al plasma ambiental. Además, la geometría del cuerpo conductor juega un papel importante en el tamaño de la vaina y, por lo tanto, en la capacidad total de recolección. Como resultado, existen varias teorías para las diferentes técnicas de recolección.
Los procesos pasivos primarios que controlan la recolección de electrones e iones en un sistema EDT son la recolección de corriente térmica, los efectos de recolección de iones por ariete, la fotoemisión de electrones y, posiblemente, la emisión secundaria de electrones e iones. Además, la recolección a lo largo de una delgada cuerda desnuda se describe utilizando la teoría de movimiento orbital limitado (OML), así como las derivaciones teóricas de este modelo dependiendo del tamaño físico con respecto a la longitud de Debye del plasma. Estos procesos tienen lugar a lo largo del material conductor expuesto de todo el sistema. Los parámetros ambientales y orbitales pueden influir significativamente en la cantidad de corriente recolectada. Algunos parámetros importantes incluyen la densidad del plasma, la temperatura de electrones e iones, el peso molecular de los iones, la intensidad del campo magnético y la velocidad orbital relativa al plasma circundante.
Luego están las técnicas de emisión y recolección activas involucradas en un sistema EDT. Esto ocurre a través de dispositivos como contactores de plasma de cátodo hueco, cátodos termoiónicos y conjuntos de emisores de campo. El diseño físico de cada una de estas estructuras, así como las capacidades de emisión actuales, se analizan en profundidad.
Cables conductores desnudos
El concepto de recolección de corriente a través de una atadura conductora desnuda fue formalizado por primera vez por Sanmartín y Martínez-Sánchez [9] . Observaron que la superficie cilíndrica de recolección de corriente más eficiente en términos de área es aquella que tiene un radio efectivo menor que ~1 longitud de Debye , donde la física de recolección de corriente se conoce como movimiento orbital limitado (OML) en un plasma sin colisiones. A medida que el radio efectivo de la atadura conductora desnuda aumenta más allá de este punto, hay reducciones predecibles en la eficiencia de recolección en comparación con la teoría OML. Además de esta teoría (que se ha derivado para un plasma sin flujo), la recolección de corriente en el espacio ocurre en un plasma que fluye, lo que introduce otro efecto de recolección. Estas cuestiones se exploran con mayor detalle a continuación.
Teoría del movimiento orbital limitado (OML)
La longitud de Debye del electrón [13] se define como la distancia de protección característica en un plasma y se describe mediante la ecuación
Esta distancia, en la que todos los campos eléctricos del plasma resultantes del cuerpo conductor han disminuido en 1/e, se puede calcular. La teoría OML [14] se define con el supuesto de que la longitud de Debye del electrón es igual o mayor que el tamaño del objeto y el plasma no fluye. El régimen OML se produce cuando la vaina se vuelve lo suficientemente gruesa como para que los efectos orbitales se vuelvan importantes en la recolección de partículas. Esta teoría tiene en cuenta y conserva la energía de las partículas y el momento angular. Como resultado, no se recolectan todas las partículas que inciden sobre la superficie de la vaina gruesa. El voltaje de la estructura colectora con respecto al plasma ambiental, así como la densidad y la temperatura del plasma ambiental, determinan el tamaño de la vaina. Este voltaje de aceleración (o desaceleración) combinado con la energía y el momento de las partículas entrantes determina la cantidad de corriente recolectada a través de la vaina de plasma.
El régimen de límite de movimiento orbital se alcanza cuando el radio del cilindro es lo suficientemente pequeño como para que todas las trayectorias de partículas entrantes que se recogen terminen en la superficie del cilindro y estén conectadas al plasma de fondo, independientemente de su momento angular inicial (es decir, ninguna está conectada a otra ubicación en la superficie de la sonda). Dado que, en un plasma sin colisiones casi neutro, la función de distribución se conserva a lo largo de las órbitas de las partículas, tener todas las "direcciones de llegada" completadas corresponde a un límite superior en la corriente recogida por unidad de área (no la corriente total). [15]
En un sistema EDT, el mejor rendimiento para una masa de anclaje dada es para un diámetro de anclaje elegido para ser menor que una longitud de Debye de electrones para condiciones ambientales ionosféricas típicas (las condiciones ionosféricas típicas en el rango de altitud de 200 a 2000 km, tienen un T_e que varía de 0,1 eV a 0,35 eV, y un n_e que varía de 10^10 m^-3 a 10^12 m^-3), por lo que está dentro del régimen OML. Se han abordado las geometrías de anclaje fuera de esta dimensión. [16] La recopilación de OML se utilizará como base al comparar los resultados de la recopilación actual para varias geometrías y tamaños de anclaje de muestra.
En 1962, Gerald H. Rosen derivó la ecuación que hoy se conoce como teoría OML de carga de polvo. [17] Según Robert Merlino, de la Universidad de Iowa, Rosen parece haber llegado a la ecuación 30 años antes que nadie. [18]
Desviaciones de la teoría OML en un plasma que no fluye
Por diversas razones prácticas, la recolección de corriente a un EDT desnudo no siempre satisface el supuesto de la teoría de recolección OML. Entender cómo el desempeño predicho se desvía de la teoría es importante para estas condiciones. Dos geometrías propuestas comúnmente para un EDT implican el uso de un alambre cilíndrico y una cinta plana. Mientras la atadura cilíndrica tenga un radio menor a una longitud de Debye, recolectará de acuerdo con la teoría OML. Sin embargo, una vez que el ancho excede esta distancia, la recolección se desvía cada vez más de esta teoría. Si la geometría de la atadura es una cinta plana, entonces se puede usar una aproximación para convertir el ancho de la cinta normalizada a un radio de cilindro equivalente. Esto fue hecho por primera vez por Sanmartin y Estes [19] y más recientemente usando el Solucionador de Plasma Cinético Bidimensional (KiPS 2-D) por Choiniere et al. [15].
Efecto de plasma que fluye
Actualmente, no existe una solución de forma cerrada para tener en cuenta los efectos del flujo de plasma en relación con la atadura desnuda. Sin embargo, Choiniere et al. han desarrollado recientemente una simulación numérica utilizando KiPS-2D que puede simular casos de flujo para geometrías simples a potenciales de polarización altos. [20] [21] Se ha discutido este análisis de plasma que fluye tal como se aplica a los EDT. [16] Este fenómeno se está investigando actualmente a través de trabajos recientes y no se comprende por completo.
Colección de cuerpos finales
En esta sección se analiza la teoría de la física del plasma que explica la recolección pasiva de corriente en un cuerpo conductor grande que se aplicará al final de una atadura de ED. Cuando el tamaño de la vaina es mucho menor que el radio del cuerpo colector, entonces, dependiendo de la polaridad de la diferencia entre el potencial de la atadura y el del plasma ambiental (V – Vp), se supone que todos los electrones o iones entrantes que ingresan a la vaina de plasma son recolectados por el cuerpo conductor. [13] [15] Se analiza esta teoría de "vaina delgada" que involucra plasmas que no fluyen, y luego se presentan las modificaciones a esta teoría para el plasma que fluye. Luego se discutirán otros mecanismos de recolección de corriente. Toda la teoría presentada se utiliza para desarrollar un modelo de recolección de corriente que tenga en cuenta todas las condiciones encontradas durante una misión EDT.
Teoría de la colección pasiva
En un plasma cuasi-neutral sin flujo y sin campo magnético, se puede suponer que un objeto conductor esférico se acumulará de manera uniforme en todas las direcciones. La acumulación de electrones e iones en el cuerpo terminal está regida por el proceso de acumulación térmica, que se da mediante Ithe e Ithi. [22]
Modo de recolección de electrones por plasma en flujo
El siguiente paso para desarrollar un modelo más realista de captación de corriente es incluir los efectos del campo magnético y los efectos del flujo de plasma. Suponiendo un plasma sin colisiones, los electrones y los iones giran alrededor de las líneas del campo magnético a medida que viajan entre los polos alrededor de la Tierra debido a las fuerzas de espejo magnético y la deriva de la curvatura del gradiente. [23] Giran en un radio y una frecuencia particulares que dependen de su masa, la intensidad del campo magnético y la energía. Estos factores deben tenerse en cuenta en los modelos de captación de corriente.

Modelo de recolección de iones de plasma en flujo
Cuando el cuerpo conductor está polarizado negativamente con respecto al plasma y viaja por encima de la velocidad térmica del ion, hay mecanismos de recolección adicionales en funcionamiento. Para las órbitas terrestres bajas (LEO) típicas, entre 200 km y 2000 km, [25] las velocidades en un marco de referencia inercial varían de 7,8 km/s a 6,9 km/s para una órbita circular y los pesos moleculares atmosféricos varían de 25,0 uma (O+, O2+ y NO+) a 1,2 uma (principalmente H+), respectivamente. [26] [27] [28] Suponiendo que las temperaturas de los electrones y los iones varían de ~0,1 eV a 0,35 eV, la velocidad iónica resultante varía de 875 m/s a 4,0 km/s desde 200 km a 2000 km de altitud, respectivamente. Los electrones viajan a aproximadamente 188 km/s en toda la LEO. Esto significa que el cuerpo en órbita viaja más rápido que los iones y más lento que los electrones, o a una velocidad mesosónica. Esto da como resultado un fenómeno único por el cual el cuerpo en órbita "embeste" a través de los iones circundantes en el plasma, creando un efecto similar a un haz en el marco de referencia del cuerpo en órbita.
Cuerpos terminales porosos
Se han propuesto cuerpos terminales porosos como una forma de reducir la resistencia de un cuerpo terminal colector mientras se mantiene idealmente una recolección de corriente similar. A menudo se modelan como cuerpos terminales sólidos, excepto que son un pequeño porcentaje del área de superficie de las esferas sólidas. Sin embargo, esto es una simplificación excesiva del concepto. Se debe aprender mucho sobre las interacciones entre la estructura de la vaina, la geometría de la malla, el tamaño del cuerpo terminal y su relación con la recolección de corriente. Esta tecnología también tiene el potencial de resolver una serie de problemas relacionados con los EDT. Los rendimientos decrecientes con la corriente de recolección y el área de resistencia han establecido un límite que los anclajes porosos podrían ser capaces de superar. Se ha realizado un trabajo sobre la recolección de corriente utilizando esferas porosas, por Stone et al. [29] [30] y Khazanov et al. [31]
Se ha demostrado que se puede estimar la corriente máxima que recoge una esfera de rejilla en comparación con la reducción de masa y de arrastre. El arrastre por unidad de corriente recogida para una esfera de rejilla con una transparencia del 80 al 90% es aproximadamente 1,2 a 1,4 veces menor que la de una esfera sólida del mismo radio. La reducción de masa por unidad de volumen, para esta misma comparación, es de 2,4 a 2,8 veces. [31]
Otros métodos de cobro actuales
Además de la captación térmica de electrones, otros procesos que podrían influir en la captación de corriente en un sistema EDT son la fotoemisión, la emisión secundaria de electrones y la emisión secundaria de iones. Estos efectos afectan a todas las superficies conductoras de un sistema EDT, no solo al cuerpo final.
Límites de carga espacial a través de las capas de plasma
En cualquier aplicación en la que se emitan electrones a través de un espacio de vacío, existe una corriente máxima admisible para una polarización dada debido a la autorepulsión del haz de electrones. Este límite de carga espacial unidimensional clásico (SCL) se deriva para partículas cargadas de energía inicial cero y se denomina Ley de Child-Langmuir. [32] [33] [34] Este límite depende del área de la superficie de emisión, la diferencia de potencial a través del espacio de plasma y la distancia de ese espacio. Se puede encontrar una discusión más amplia de este tema. [35] [36] [37] [38]
Emisores de electrones
Existen tres tecnologías de emisión de electrones activos que suelen considerarse para aplicaciones de EDT: contactores de plasma de cátodo hueco (HCPC), cátodos termoiónicos (TC) y cátodos de emisión de campo (FEC), a menudo en forma de matrices de emisores de campo (FEA). Se presentarán configuraciones a nivel de sistema para cada dispositivo, así como los costos, beneficios y validación relativos.
Cátodo termoiónico (TC)
La emisión termoiónica es el flujo de electrones desde una superficie de metal o de óxido de metal cargada y calentada, causada por la energía vibracional térmica que supera la función de trabajo (fuerzas electrostáticas que mantienen a los electrones en la superficie). La densidad de corriente de emisión termoiónica, J, aumenta rápidamente con el aumento de la temperatura, liberando una cantidad significativa de electrones en el vacío cerca de la superficie. La relación cuantitativa se da en la ecuación
Esta ecuación se llama ecuación de Richardson-Dushman o de Richardson. (ф es aproximadamente 4,54 eV y AR ~120 A/cm2 para el tungsteno). [39]
Una vez que los electrones son emitidos termoiónicamente desde la superficie del TC, requieren un potencial de aceleración para cruzar un espacio, o en este caso, la envoltura de plasma. Los electrones pueden alcanzar esta energía necesaria para escapar del SCL de la envoltura de plasma si se utiliza una rejilla acelerada, o cañón de electrones. La ecuación
muestra qué potencial se necesita a través de la red para emitir una determinada corriente que ingresa al dispositivo. [40] [41]
Aquí, η es la eficiencia del conjunto de cañones de electrones (EGA) (~0,97 en TSS-1), ρ es la permeabilidad del EGA (7,2 micropervs en TSS-1), ΔV tc es el voltaje a través de la rejilla de aceleración del EGA e I t es la corriente emitida. [40] La permeabilidad define la corriente limitada por la carga espacial que se puede emitir desde un dispositivo. La siguiente figura muestra ejemplos comerciales de emisores termoiónicos y cañones de electrones producidos en Heatwave Labs Inc.

La emisión de electrones en el TC se producirá en uno de dos regímenes diferentes: flujo de corriente limitado por temperatura o por carga espacial. En el caso del flujo limitado por temperatura, se emite cada electrón que obtiene suficiente energía para escapar de la superficie del cátodo, suponiendo que el potencial de aceleración del cañón de electrones sea lo suficientemente grande. En este caso, la corriente de emisión está regulada por el proceso de emisión termoiónica, dado por la ecuación de Richardson Dushman. En el flujo de corriente de electrones en el SCL, hay tantos electrones emitidos desde el cátodo que no todos son acelerados lo suficiente por el cañón de electrones para escapar de la carga espacial. En este caso, el potencial de aceleración del cañón de electrones limita la corriente de emisión. El siguiente gráfico muestra las corrientes limitadoras de temperatura y los efectos del SCL. A medida que aumenta la energía del haz de electrones, se puede ver que aumenta el total de electrones que escapan. Las curvas que se vuelven horizontales son casos limitados por temperatura.

Cátodo de emisión de campo (FEC)

En la emisión de electrones de campo , los electrones atraviesan una barrera de potencial, en lugar de escapar por encima de ella como en la emisión termoiónica o la fotoemisión. [43] Para un metal a baja temperatura, el proceso se puede entender en términos de la figura siguiente. El metal se puede considerar una caja de potencial, llena de electrones hasta el nivel de Fermi (que se encuentra por debajo del nivel de vacío por varios electronvoltios). El nivel de vacío representa la energía potencial de un electrón en reposo fuera del metal en ausencia de un campo externo. En presencia de un campo eléctrico fuerte, el potencial fuera del metal se deformará a lo largo de la línea AB, de modo que se forma una barrera triangular, a través de la cual los electrones pueden hacer un túnel. Los electrones se extraen de la banda de conducción con una densidad de corriente dada por la ecuación de Fowler-Nordheim.

AFN y BFN son las constantes determinadas por mediciones del FEA con unidades de A/V2 y V/m, respectivamente. EFN es el campo eléctrico que existe entre la punta emisora de electrones y la estructura polarizada positivamente que extrae los electrones. Las constantes típicas para los cátodos de tipo Spindt incluyen: AFN = 3,14 x 10-8 A/V2 y BFN = 771 V/m. (Hoja de datos del Stanford Research Institute). Una estructura de aceleración se coloca típicamente en estrecha proximidad con el material emisor como en la siguiente figura. [44] La proximidad cercana ( escala micrométrica ) entre el emisor y la compuerta, combinada con estructuras de enfoque naturales o artificiales, proporciona de manera eficiente las altas intensidades de campo requeridas para la emisión con voltaje y potencia aplicados relativamente bajos.
Se probó con éxito un cátodo de emisión de campo de nanotubos de carbono en el experimento de anclaje electrodinámico KITE en el vehículo de transferencia japonés H-II. [45]
Los cátodos de emisión de campo suelen adoptar la forma de matrices de emisores de campo (FEA), como el diseño de cátodo de Spindt et al. La siguiente figura muestra imágenes visuales en primer plano de un emisor de Spindt. [46] [47] [48]

Se han desarrollado diversos materiales para matrices de emisores de campo, que van desde silicio hasta puntas de molibdeno fabricadas con semiconductores con compuertas integradas hasta una placa de nanotubos de carbono distribuidos aleatoriamente con una estructura de compuerta separada suspendida encima. [44] Las ventajas de las tecnologías de emisión de campo sobre los métodos alternativos de emisión de electrones son:
- No se requiere un consumible (gas) y no hay consideraciones de seguridad resultantes para manipular un recipiente presurizado.
- Una capacidad de bajo consumo
- Teniendo impactos de potencia moderados debido a límites de carga espacial en la emisión de los electrones hacia el plasma circundante.
Un aspecto importante a tener en cuenta en el caso de los emisores de campo es el efecto de la contaminación. Para lograr la emisión de electrones a voltajes bajos, las puntas de los conjuntos de emisores de campo se construyen a escala micrométrica. Su rendimiento depende de la construcción precisa de estas pequeñas estructuras. También dependen de que estén construidas con un material que posea una función de trabajo baja. Estos factores pueden hacer que el dispositivo sea extremadamente sensible a la contaminación, especialmente de hidrocarburos y otras moléculas grandes que se polimerizan fácilmente. [44] Las técnicas para evitar, eliminar u operar en presencia de contaminaciones en pruebas terrestres y entornos ionosféricos (por ejemplo, desgasificación de naves espaciales) son fundamentales. La investigación en la Universidad de Michigan y en otros lugares se ha centrado en este problema de desgasificación. Se están desarrollando carcasas protectoras, limpieza de electrones, recubrimientos robustos y otras características de diseño como posibles soluciones. [44] Los FEA utilizados para aplicaciones espaciales aún requieren la demostración de estabilidad a largo plazo, repetibilidad y confiabilidad de operación a potenciales de compuerta adecuados para las aplicaciones espaciales. [49]
Cátodo hueco
Los cátodos huecos emiten una densa nube de plasma ionizando primero un gas. Esto crea una columna de plasma de alta densidad que entra en contacto con el plasma circundante. La región entre la columna de alta densidad y el plasma circundante se denomina doble vaina o doble capa. Esta doble capa es esencialmente dos capas adyacentes de carga. La primera capa es una capa positiva en el borde del plasma de alto potencial (la nube de plasma del contactor). La segunda capa es una capa negativa en el borde del plasma de bajo potencial (el plasma ambiental). Varias personas han realizado investigaciones adicionales sobre el fenómeno de la doble capa. [50] [51] [52] [53] Un tipo de cátodo hueco consiste en un tubo de metal revestido con un inserto de tungsteno impregnado con óxido de bario sinterizado, cubierto en un extremo por una placa con un pequeño orificio, como se muestra en la siguiente figura. [54] [55] Los electrones se emiten desde el inserto impregnado con óxido de bario por emisión termoiónica. Un gas noble fluye hacia la región de inserción del HC y es ionizado parcialmente por los electrones emitidos que son acelerados por un campo eléctrico cerca del orificio (el xenón es un gas común utilizado para los HC, ya que tiene una energía de ionización específica baja (potencial de ionización por unidad de masa). Para fines de EDT, una masa menor sería más beneficiosa porque la masa total del sistema sería menor. Este gas solo se utiliza para el intercambio de carga y no para la propulsión). Muchos de los átomos de xenón ionizado se aceleran hacia las paredes, donde su energía mantiene la temperatura de emisión termoiónica. El xenón ionizado también sale por el orificio. Los electrones se aceleran desde la región de inserción, a través del orificio hasta el guardián, que siempre tiene un sesgo más positivo.

En el modo de emisión de electrones, el plasma ambiental está polarizado positivamente con respecto al guardián. En el plasma del contactor, la densidad de electrones es aproximadamente igual a la densidad de iones. Los electrones de mayor energía fluyen a través de la nube de iones que se expande lentamente, mientras que los electrones de menor energía quedan atrapados dentro de la nube por el potencial del guardián. [55] Las altas velocidades de los electrones conducen a corrientes de electrones mucho mayores que las corrientes de iones de xenón. Por debajo del límite de saturación de emisión de electrones, el contactor actúa como una sonda de emisión bipolar. Cada ion saliente generado por un electrón permite que se emitan varios electrones. Este número es aproximadamente igual a la raíz cuadrada de la relación entre la masa del ion y la masa del electrón.
En el gráfico siguiente se puede ver cómo se ve una curva IV típica para un cátodo hueco en modo de emisión de electrones. Dada una determinada geometría del dispositivo de retención (el anillo en la figura anterior por donde salen los electrones), una tasa de flujo de iones y Vp, se puede determinar el perfil IV. [54] [55] [56] [111-113].
El funcionamiento del HC en el modo de recolección de electrones se denomina modo operativo de contacto de plasma (o encendido). El “modo encendido” se denomina así porque indica que se pueden lograr niveles de corriente de varios amperios utilizando la caída de voltaje en el contactor de plasma. Esto acelera los electrones del plasma espacial que ionizan el flujo de expelente neutro del contactor. Si las corrientes de recolección de electrones son altas y/o las densidades de electrones ambientales son bajas, la envoltura en la que se mantiene la recolección de corriente de electrones simplemente se expande o se encoge hasta que se recolecta la corriente requerida.
Además, la geometría afecta la emisión del plasma del HC como se ve en la figura siguiente. Aquí se puede ver que, dependiendo del diámetro y el espesor del retenedor y la distancia de este con respecto al orificio, el porcentaje total de emisión puede verse afectado. [57]

Resumen de la recolección y emisión de plasma
Todas las técnicas de emisión y recolección de electrones se pueden resumir en la siguiente tabla. Para cada método hay una descripción de si los electrones o iones en el sistema aumentaron o disminuyeron en función del potencial de la nave espacial con respecto al plasma. Los electrones (e-) y los iones (iones+) indican que el número de electrones o iones aumenta (↑) o se reduce (↓). Además, para cada método se aplican algunas condiciones especiales (consulte las secciones respectivas de este artículo para obtener más aclaraciones sobre cuándo y dónde se aplican).
Emisión /recolección pasiva de iones y electrones V − V p < 0 V − V p > 0 Anclaje desnudo: OML iones + ↑ mi − ↑ Colección de carneros iones + ↑ 0 Recolección térmica iones + ↑ mi − ↑ Fotoemisión mi − ↓ y − ↓,~0 Emisión secundaria de electrones mi − ↓ mi − ↓ Emisión de iones secundarios iones + ↓,~0 0 Régimen de retardación mi − ↑ iones + ↑, ~0 Emisión activa de iones y electrones El potencial no importa Emisión termoiónica mi − ↓ Conjuntos de emisores de campo mi − ↓ Cátodos huecos mi − ↓ mi − ↑
Para su uso en el modelado de sistemas EDT, cada uno de los modelos de teoría de emisión y recolección pasiva de electrones se ha verificado mediante la reproducción de ecuaciones y resultados publicados previamente. Estos gráficos incluyen: teoría limitada del movimiento orbital, [15] recolección de RAM y recolección térmica, [58] fotoemisión, [59] emisión secundaria de electrones, [60] y emisión secundaria de iones. [61] [62] [63] [64]
Fundamentos de los sistemas de anclaje electrodinámicos
Para integrar todos los emisores y colectores de electrones y la teoría más reciente en un único modelo, primero se debe definir y derivar el sistema EDT. Una vez logrado esto, será posible aplicar esta teoría para determinar optimizaciones de los atributos del sistema.
Hay una serie de derivaciones que resuelven numéricamente los potenciales y corrientes involucrados en un sistema EDT. [65] [66] [67] [68] Se describe la derivación y la metodología numérica de un sistema EDT completo que incluye una sección de anclaje desnudo, anclaje conductor aislante, emisores de electrones (e iones) en el cuerpo final y recolección pasiva de electrones. A esto le sigue el modelo simplificado de anclaje completamente aislado. Luego se discutirán los fenómenos EDT especiales y la verificación del modelo del sistema EDT utilizando datos de misiones experimentales.
Derivación del sistema de anclaje desnudo
Una nota importante sobre la derivación de la EDT se refiere al cuerpo celeste que orbita el sistema de anclaje. Por cuestiones prácticas, se utilizará la Tierra como el cuerpo que orbita; sin embargo, esta teoría se aplica a cualquier cuerpo celeste con una ionosfera y un campo magnético.
Las coordenadas son lo primero que se debe identificar. Para los fines de esta derivación, los ejes x e y se definen como las direcciones este-oeste y norte-sur con respecto a la superficie de la Tierra, respectivamente. El eje z se define como arriba-abajo desde el centro de la Tierra, como se ve en la figura siguiente. Los parámetros (campo magnético B , longitud de la cuerda L y velocidad orbital v orb ) son vectores que se pueden expresar en términos de este sistema de coordenadas, como en las siguientes ecuaciones:
- (el vector del campo magnético),
- (el vector de posición de la atadura), y
- (el vector de velocidad orbital).
Los componentes del campo magnético se pueden obtener directamente del modelo de Campo Geomagnético de Referencia Internacional (IGRF). Este modelo es el resultado de un esfuerzo colaborativo entre los modeladores de campos magnéticos y los institutos que participan en la recopilación y difusión de datos de campos magnéticos de satélites y de observatorios y estudios de todo el mundo. Para esta derivación, se supone que las líneas de campo magnético tienen el mismo ángulo a lo largo de la cuerda y que esta es rígida.
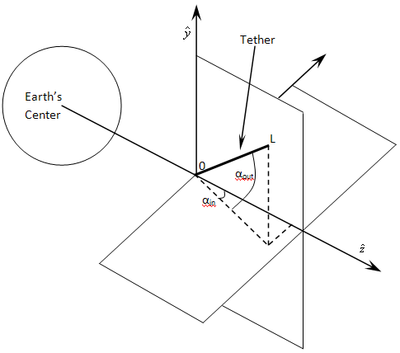
De manera realista, las fuerzas electrodinámicas transversales hacen que la atadura se arquee y se aleje de la vertical local. Las fuerzas del gradiente de gravedad producen entonces una fuerza restauradora que tira de la atadura hacia la vertical local; sin embargo, esto da como resultado un movimiento similar al de un péndulo (las fuerzas del gradiente de gravedad también dan como resultado movimientos pendulares sin fuerzas de DE). La dirección B cambia a medida que la atadura orbita la Tierra y, por lo tanto, la dirección y la magnitud de las fuerzas de DE también cambian. Este movimiento de péndulo puede convertirse en libraciones complejas tanto en la dirección en el plano como fuera del plano. Luego, debido al acoplamiento entre el movimiento en el plano y las oscilaciones elásticas longitudinales, así como al acoplamiento entre los movimientos en el plano y fuera del plano, una atadura electrodinámica operada a una corriente constante puede agregar continuamente energía a los movimientos de libración. Este efecto tiene entonces la posibilidad de hacer que las amplitudes de libración crezcan y eventualmente causen oscilaciones salvajes, incluida una como el "efecto de la cuerda para saltar", [69] pero eso está más allá del alcance de esta derivación. En un sistema EDT no giratorio (un sistema giratorio, llamado Reimpulso Electrodinámico por Intercambio de Momento [MXER]), la atadura está predominantemente en la dirección z debido a la alineación del gradiente de gravedad natural con la Tierra.
Derivaciones
La siguiente derivación describirá la solución exacta del sistema que tiene en cuenta todas las cantidades vectoriales involucradas y luego una segunda solución con la condición nominal donde el campo magnético, la velocidad orbital y la orientación de la atadura son todos perpendiculares entre sí. La solución final del caso nominal se resuelve en términos de la densidad electrónica, n_e, la resistencia de la atadura por unidad de longitud, R_t, y la potencia de la fuente de alimentación de alto voltaje, P_hvps.
La siguiente figura describe un sistema EDT típico en una configuración de compuerta conectada a tierra con polarización en serie (se han presentado descripciones adicionales de los diversos tipos de configuraciones analizadas [16] ) con una ampliación de una sección infinitesimal de una atadura desnuda. Esta figura está configurada simétricamente para que cualquiera de los extremos se pueda utilizar como ánodo. Este sistema de atadura es simétrico porque los sistemas de atadura giratorios necesitarán utilizar ambos extremos como ánodos y cátodos en algún punto de su rotación. El V_hvps solo se utilizará en el extremo del cátodo del sistema EDT y se desactivará en caso contrario.
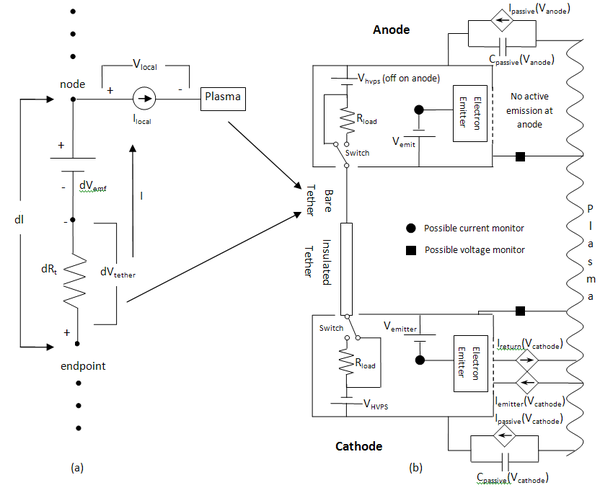
La dirección en el plano y fuera del plano está determinada por el vector de velocidad orbital del sistema. Una fuerza en el plano está en la dirección del desplazamiento. Agregará o quitará energía a la órbita, aumentando así la altitud al cambiar la órbita a una elíptica. Una fuerza fuera del plano está en la dirección perpendicular al plano del desplazamiento, lo que provoca un cambio en la inclinación. Esto se explicará en la siguiente sección.
Para calcular las direcciones en el plano y fuera del plano, se deben obtener los componentes de los vectores de velocidad y campo magnético y calcular los valores de fuerza. El componente de la fuerza en la dirección de desplazamiento servirá para mejorar las capacidades de elevación de la órbita, mientras que el componente fuera del plano del empuje alterará la inclinación. En la figura siguiente, el vector del campo magnético está únicamente en la dirección norte (o eje y), y se pueden ver las fuerzas resultantes en una órbita, con cierta inclinación. Una órbita sin inclinación tendría todo el empuje en la dirección en el plano. [70]
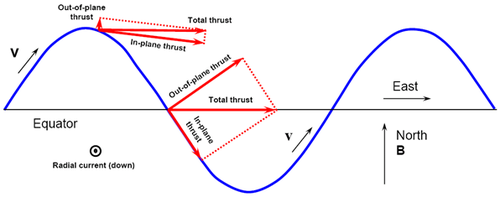 |  |
Se han realizado trabajos para estabilizar las libraciones del sistema de amarre para evitar la desalineación del amarre con el gradiente de gravedad. La siguiente figura muestra los efectos de arrastre que encontrará un sistema EDT en una órbita típica. El ángulo en el plano, α_ip, y el ángulo fuera del plano, α_op, se pueden reducir aumentando la masa final del sistema o empleando tecnología de retroalimentación. [69] Cualquier desviación en la alineación de la gravedad debe comprenderse y tenerse en cuenta en el diseño del sistema.
Viajes interestelares
Se ha considerado e investigado una aplicación del sistema EDT para viajes interestelares utilizando el medio interestelar local de la Burbuja Local . Se ha descubierto que es factible utilizar el sistema EDT para suministrar energía a bordo dada una tripulación de 50 personas con un requisito de 12 kilovatios por persona. La generación de energía se logra a expensas de la energía cinética de la nave espacial. A la inversa, el sistema EDT podría usarse para la aceleración. Sin embargo, se ha descubierto que esto es ineficaz. El giro sin empuje utilizando el sistema EDT es posible para permitir la corrección del curso y el encuentro en el espacio interestelar. Sin embargo, no permitirá un rápido giro sin empuje para permitir que una nave espacial vuelva a entrar en un haz de energía o haga numerosos pases solares debido a un radio de giro extremadamente grande de 3,7*10 13 km (~3,7 años luz ). [71]
Véase también
Referencias
- información general
- Cosmo, ML, y Lorenzini, EC, "Tethers in Space Handbook", Centro de vuelo espacial Marchall de la NASA, 1997, págs. 274–1-274.
- Mariani, F., Candidi, M., Orsini, S., "Flujo de corriente a través de vainas de alto voltaje observado por el experimento TEMAG durante TSS-1R", Geophysical Research Letters, vol. 25, núm. 4, 1998, págs. 425–428.
- Citas
- ^ ab NASA, Tethers In Space Handbook, editado por ML Cosmo y EC Lorenzini, tercera edición, diciembre de 1997 (consultado el 20 de octubre de 2010); véase también la versión en NASA MSFC Archivado el 27 de octubre de 2011 en Wayback Machine ; disponible en scribd
- ^ Messier, Doug (12 de marzo de 2012). «Company Gets $1.9 Million from NASA to Develop Debris Removal Spacecraft» (La empresa obtiene 1,9 millones de dólares de la NASA para desarrollar una nave espacial de eliminación de escombros). Parabolic Arc (Arco parabólico) . Consultado el 15 de marzo de 2012 .
- ^ por Johnson & Herrmann (1998). "Estudio de reactivación del anclaje electrodinámico de la Estación Espacial Internacional" (PDF) .
- ^ Fuhrhop, KR, Gilchrist, BE, Bilen, SG, "Análisis del sistema del rendimiento esperado del amarre electrodinámico para la misión ProSEDS", 39.ª Conferencia de propulsión conjunta AIAA/ASME/SAE/ASEE, AIAA, 2003, págs. 1–10.
- ^ Johnson, L., Estes, RD, Lorenzini, EC, "Experimento de sistema de despliegue de propulsión con material fungible pequeño", Journal of Spacecraft and Rockets, vol. 37, núm. 2, 2000, págs. 173-176.
- ^ Lorenzini, EC, Welzyn, K. y Cosmo, ML, "Dinámica de implementación esperada de ProSEDS", 39.ª Conferencia y exhibición conjunta sobre propulsión AIAA/ASME/SAE/ASEE, AIAA, 2003, págs. 1–9.
- ^ Sanmartin, JR, Charro, M., Lorenzini, EC, "Análisis de la prueba ProSEDS de recolección de cables desnudos", 39.ª Conferencia y exhibición conjunta sobre propulsión AIAA/ASME/SAE/ASEE, AIAA, 2003, págs. 1–7.
- ^ Vaughn, JA, Curtis, L., Gilchrist, BE, "Revisión del desarrollo de la misión de amarre electrodinámico ProSEDS", 40.ª Conferencia y exhibición conjunta de propulsión AIAA/ASME/SAE/ASEE, AIAA, 2004, págs. 1–12.
- ^ ab Sanmartin, JR, Martinez-Sanchez, M., y Ahedo, E., "Ánodos de alambre desnudo para amarres electrodinámicos", Journal of Propulsion and Power, vol. 9, núm. 3, 1993, págs. 353–360
- ^ Generador de energía para satélites en órbita terrestre. Thomas G. Roberts et al.
- ^ Katz, I.; Lilley, JR Jr.; Greb, A. (1995). "Recolección de corriente mejorada por turbulencia de plasma: resultados del vuelo de amarre electrodinámico del generador de motor de plasma". J. Geophys. Res . 100 (A2): 1687–90. Código Bibliográfico :1995JGR...100.1687K. doi :10.1029/94JA03142.
- ^ Patente estándar de EE. UU. 6116544, Forward & Hoyt, Correa electrodinámica y método de uso, 1986
- ^ ab Lieberman, MA, y Lichtenberg, AJ, "Principios de descargas de plasma y procesamiento de materiales", Wiley-Interscience, Hoboken, NJ, 2005, págs. 757.
- ^ Mott-Smith, HM, y Langmuir, I., "La teoría de los colectores en descargas gaseosas", Physical Review, vol. 28, 1926, págs. 727–763.
- ^ abcd Choinere, E., "Teoría y evaluación experimental de un modelo cinético consistente de estado estable para estructuras conductoras 2-D en plasmas ionosféricos con aplicación a ataduras electrodinámicas desnudas en el espacio", 2004, págs. 1–313.
- ^ abc Fuhrhop, KRP, “Teoría y evaluación experimental de sistemas de anclaje electrodinámicos y tecnologías relacionadas”, tesis doctoral de la Universidad de Michigan, 2007, págs. 1-307. "Teoría y evaluación experimental de sistemas de anclaje electrodinámicos y tecnologías relacionadas" (PDF) . Archivado desde el original (PDF) el 2011-08-14 . Consultado el 2011-04-04 .
- ^ Rosen, G. (1962). "Método para la eliminación de electrones libres en un plasma". Phys. Fluids . 5 (6): 737. Bibcode :1962PhFl....5..737R. doi : 10.1063/1.1706691 .
- ^ Correo electrónico de Robert Merlino a Gerald Rosen, 22 de enero de 2010 Archivado el 29 de abril de 2014 en Wayback Machine.
- ^ Sanmartin, JR, y Estes, RD, "El régimen limitado por el movimiento orbital de las sondas cilíndricas Langmuir", Physics of Plasmas, vol. 6, núm. 1, 1999, págs. 395-405.
- ^ Choiniere, E., Gilchrist, BE, Bilen, SG, "Medición de los efectos de la geometría de la sección transversal en la recolección de electrones por sondas largas en plasmas de flujo mesosónico", 39.ª Conferencia y exhibición conjunta sobre propulsión AIAA/ASME/SAE/ASEE, AIAA, 2003, págs. 1–13.
- ^ Choiniere, E., y Gilchrist, BG, "Investigación de los efectos del flujo de plasma ionosférico en la recolección de corriente en cables paralelos utilizando simulaciones cinéticas de estado estable autoconsistentes", 41.ª Conferencia y exhibición conjunta de propulsión AIAA/ASME/SAE/ASEE, AIAA, 2005, págs. 1–13.
- ^ Parker, LW, "Teoría de envoltura plasmática y envoltura fotográfica para grandes estructuras espaciales de alto voltaje", editado por HB Garrett y CP Pike, Sistemas espaciales y sus interacciones con el entorno espacial de la Tierra, AIAA Press, 1980, págs. 477–491.
- ^ Gombosi, TI, "Física de entornos espaciales", Dessler, AJ Houghton, JT y Rycroft, MJ eds., Cambridge University Press, Cambridge, Reino Unido, 1998, págs. 1–339.
- ^ Stone, NH, y Bonifazi, C., "La misión TSS-1R: descripción general y contexto científico", Geophysical Research Letters, vol. 25, n.º 4, 1998, págs. 409-412.
- ^ Gregory, FD, "Directrices de normas de seguridad de la NASA y procedimientos de evaluación para limitar los desechos orbitales", NASA, NSS 1740.14, Washington DC, 1995
- ^ Bilitza, D., "Ionosfera de referencia internacional 2000", Radio Science, vol. 36, núm. 2, 2001, págs. 261-275.
- ^ Bilitza, D., "Ionosfera de referencia internacional: situación 1995/96", Advanced Space Research, vol. 20, núm. 9, 1997, págs. 1751-1754.
- ^ Wertz, JR, y Larson, WJ eds., "Análisis y diseño de misiones espaciales", Microcosm Press y Kluwar Academic Publishers, El Segundo, CA, 1999, págs. 1–985.
- ^ Stone, NH, y Gierow, PA, "Una evaluación preliminar de contactores de plasma pasivos de cuerpo final", 39.ª Reunión y Exhibición de Ciencias Aeroespaciales, AIAA, 2001, págs. 1–6.
- ^ Stone, NH, y Moore, JD, "Electrodos de esfera de rejilla utilizados para la recolección de corriente en el polo positivo de los anclajes electrodinámicos", 45.ª Conferencia de estructuras, dinámica estructural y materiales de la AIAA/ASME/ASCE/AHS/ASC, AIAA, 2004, págs. 1–7.
- ^ ab Khazanov, GV, Krivorutsky, E., y Sheldon, RB, "Recolección de corriente de esferas sólidas y de cuadrícula en vista de los resultados de las misiones del sistema de satélites atados TSS 1 y TSS 1R", Journal of Goephysical Research, vol. 110, 2005, págs. 1-10.
- ^ Niño, CD , "Descarga de CaO caliente", Physical Review (Serie I), Vol. 32, No. 5, 1911, págs. 492–511.
- ^ Langmuir, I. , "El efecto de la carga espacial y las velocidades iniciales en la distribución de potencial y la corriente termoiónica entre electrodos planos paralelos", Physical Review, vol. 21, n.º 4, 1923, págs. 419-435
- ^ Langmuir, I., "El efecto de la carga espacial y los gases residuales en las corrientes termoiónicas en alto vacío", Physical Review, vol. 2, núm. 6, 1913, págs. 450-486.
- ^ Luginsland, JW, McGee, S. y Lau, YY, "Formación de cátodo virtual debido a transitorios electromagnéticos", IEEE Transactions on Plasma Science, vol. 26, n.º 3, 1998, págs. 901-904.
- ^ Lau, YY, "Teoría simple para la ley de Child-Langmuir bidimensional", Physical Review Letters, vol. 87, núm. 27, 2001, págs. 278301/1-278301/3.
- ^ Luginsland, JW, Lau, YY y Gilgenbach, RM, "Ley de Child-Langmuir bidimensional", Physical Review Letters, vol. 77, núm. 22, 1996, págs. 4668–4670.
- ^ Humphries, SJ, "Haces de partículas cargadas", John Wiley & Sons, Inc., Nueva York, 1990, págs. 834.
- ^ Dekker, AJ, "Emisión termoiónica", McGraw Hill Access Science Encyclopedia, vol. 2004, núm. 5/3, 2002, págs. 2.
- ^ ab Dobrowolny, M. y Stone, NH, "Una descripción técnica de TSS-1: la primera misión del sistema de satélites conectados", Il Nuovo Cimento Della Societa Italiana Di Fisica, vol. 17C, núm. 1, 1994, págs. 1–12.
- ^ Bonifazi, C., Svelto, F. y Sabbagh, J., "TSS Core Equipment I: paquete electrodinámico y fundamento para el análisis electrodinámico del sistema", Il Nuovo Cimento Della Societa Italiana Di Fisica, vol. 17C, núm. 1, 1994, págs. 13–47.
- ^ Gunther, K., "Cita de fuente de iones/cátodo hueco", HeatWave Labs, Inc., 3968, Watsonville, CA, 2006.
- ^ ab Gomer, R., "Emisión de campo", McGraw Hill Access Science Encyclopedia, Vol. 2005, No. 1 de julio de 2002, págs. 2.
- ^ abcd Morris, D., "Optimización de los límites de carga espacial de la emisión de electrones en plasmas en la propulsión eléctrica espacial", Universidad de Michigan, 2005, págs. 1–212.
- ^ Ohkawa, Y., (diciembre de 2020). "Revisión de KITE - Experimento de anclaje electrodinámico en el vehículo de transferencia japonés H-II", Acta Astronautica, vol. 177 , págs. 750-758. https://doi.org/10.1016/j.actaastro.2020.03.014 Consultado el 16 de julio de 2021.
- ^ Spindt, CA, Holland, CE y Rosengreen, A. Brodie, I., "Matrices de emisores de campo para microelectrónica de vacío", IEEE Transactions on Electron Devices, vol. 38, n.º 10, 1991, págs. 2355-2363.
- ^ Spindt, CA, "Spindt Emitter Measurements", material inédito Stanford Research Institute, 2001, págs. 1.
- ^ Jensen, KL, "Conjuntos de emisores de campo para aplicaciones de fuentes de plasma y microondas", Physics of Plasmas, vol. 6, n.º 5, 1999, págs. 2241-2253.
- ^ Gilchrist, BE, Gallimore, AD, Jensen, KL, "Cátodos de matriz de emisores de campo (FEAC) para aplicaciones espaciales: una tecnología facilitadora", no publicado, Universidad de Michigan, 2001.
- ^ Lapuerta, V., y Ahedo, E., "Modelo dinámico de una estructura de plasma con una doble capa intermedia, formada fuera de un contactor de plasma anódico", Physics of Plasmas, Vol. 7, No. 6, 2000, pp. 2693–2703.
- ^ Wells, AA, "Flujo de corriente a través de una doble capa de plasma en un propulsor iónico de cátodo hueco", 9.ª Conferencia de propulsión eléctrica de la AIAA, AIAA, 1972, págs. 1-15.
- ^ Andrews, JG, y Allen, JE, "Teoría de una doble envoltura entre dos plasmas", Actas de la Royal Society of London Serie A, vol. 320, núm. 1543, 1971, págs. 459-472.
- ^ Prewett, PD, y Allen, JE, "La doble vaina asociada con un cátodo caliente", Actas de la Royal Society of London Serie A, Vol. 348, No. 1655, 1976, págs. 435–446.
- ^ abc Katz, I., Anderson, JR, Polk, JE, "Modelo de cátodo hueco unidimensional", Journal of Propulsion and Power, vol. 19, n.º 4, 2003, págs. 595–600.
- ^ abc Katz, I., Lilley, JR Jr., Greb, A., "Recolección de corriente mejorada por turbulencia de plasma: resultados del vuelo de amarre electrodinámico del generador de motor de plasma", Journal of Geophysical Research, vol. 100, n.º A2, 1995, págs. 1687-1690.
- ^ ab Parks, DE, Katz, I., Buchholtz, B., "Características de expansión y emisión de electrones de un contactor de plasma de cátodo hueco", Journal of Applied Physics, Vol. 74, No. 12, 2003, págs. 7094–7100.
- ^ ab Domonkos, MT, "Evaluación de cátodos huecos con orificios de baja corriente", tesis doctoral de la Universidad de Michigan, 1999, págs. 1-173.
- ^ Aguero, VM, "Un estudio de la carga eléctrica en naves espaciales LEO de gran tamaño utilizando un satélite atado como referencia de plasma remota", Stanford University, Space, Telecommunications and Radioscience Laboratory, 1996, págs. 1-192
- ^ Whipple, EC, "Potenciales de superficies en el espacio", Informe de progreso en física, vol. 44, 1981, págs. 1197-1250.
- ^ Hastings, D., y Garrett, H., "Interacciones entre naves espaciales y medio ambiente", Cambridge University Press, Nueva York, NY, 1996, págs. 292.
- ^ Siegel, MW, y Vasile, MJ, "Nuevo analizador de gran angular y alta energía de transmisión para espectrometría de masas de iones secundarios", Review of Scientific Instrumentation, vol. 52, n.º 11, 1981, págs. 1603-1615.
- ^ Benninghoven, A., "Desarrollos en espectroscopia de masas de iones secundarios y aplicaciones a los estudios de superficies", Surface Science, vol. 53, 1975, págs. 596-625
- ^ Benninghoven, A., "Investigación de superficies de sólidos mediante el método estadístico de espectroscopia de masas de iones secundarios (SIMS)", Surface Science, vol. 35, 1973, págs. 427–457.
- ^ Benninghoven, A., y Mueller, A., "Los rendimientos de iones secundarios son cercanos a 1 para algunos compuestos químicos", Physics Letters, vol. 40A, núm. 2, 1972, págs. 169-170.
- ^ Dobrowolny, M., "Electrodinámica de largas ataduras metálicas en el plasma ionosférico", Radio Science, vol. 13, núm. 3, 1978, págs. 417–424.
- ^ Arnold, DA, y Dobrowolny, M., "Modelo de línea de transmisión de la interacción de un cable metálico largo con la ionosfera", Radio Science, vol. 15, núm. 6, 1980, págs. 1149-1161.
- ^ Dobrowolny, M., Vannaroni, G. y DeVenuto, F., "Desorbitamiento electrodinámico de satélites LEO", Nuovo Cimento, vol. 23C, núm. 1, 2000, págs. 1–21.
- ^ Dobrowolny, M., Colombo, G. y Grossi, MD, "Electrodinámica de cables conductores largos en el entorno cercano a la Tierra", Informe provisional del Observatorio Astrofísico Smithsoniano, 1976, págs. 1–48.
- ^ abc Hoyt, RP, "Estabilización de amarres electrodinámicos", 38.ª Conferencia y exposición conjunta sobre propulsión AIAA/ASME/SAE/ASEE, 2002, págs. 1–9.
- ^ Bonometti, JA, Sorensen, KF, Jansen, RH, "Atadura electrodinámica de reimpulso gratuito en la Estación Espacial Internacional", 41.ª Conferencia y exposición conjunta sobre propulsión AIAA/ASME/SAE/ASEE, AIAA, 2005, págs. 1–7.
- ^ "Aplicaciones de la atadura electrodinámica a los viajes interestelares" Gregory L. Matloff, Less Johnson, febrero de 2005
Lectura adicional
- Dobrowolny, M. (1979). Fenómenos de ondas y partículas inducidos por una atadura electrodinámica . Informe especial de la SAO, 388. Cambridge, Mass: Observatorio Astrofísico del Instituto Smithsoniano.
- Williamson, PR (1986). Características de alto voltaje de la atadura electrodinámica y la generación de energía y propulsión . Informe final. [Informe del contratista de la NASA], NASA CR-178949. Washington, DC: Administración Nacional de Aeronáutica y del Espacio.
Enlaces externos
- Patentes relacionadas
- Patente estadounidense 3.174.705 , " Estación espacial y sistema para operarla ".
- Patente estadounidense 3.205.381 , " Batería ionosférica ".
- Patente estadounidense 4.097.010 , " Satélite conectado por medio de una larga cuerda a una nave espacial propulsada ".
- Patente de EE. UU. 6.116.544 , " Anclaje electrodinámico y método de uso ".
- Publicaciones
- Samanta Roy, RI; Hastings, DE; Ahedo, E. (1992). "Análisis de sistemas de ataduras electrodinámicas". J Spacecr Rockets . 29 (3): 415–424. Código Bibliográfico :1992JSpRo..29..415S. doi :10.2514/3.26366.
- Ahedo, E.; Sanmartin, JR (marzo-abril de 2002). "Análisis de sistemas de anclaje desnudo para desorbitar satélites de órbita baja". J Spacecr Rockets . 39 (2): 198–205. Bibcode :2002JSpRo..39..198A. doi :10.2514/2.3820.
- Peláez, J.; Sánchez-Arriaga, G.; Sanjurjo-Rivo, M. (octubre de 2012). Correas electrodinámicas autoequilibradas para la mitigación de desechos espaciales. 57ª Conferencia Astronáutica Internacional. Valencia, España: AIAA . doi :10.2514/6.IAC-06-B6.4.03. ISBN 978-1-62410-042-0. Recuperado el 6 de noviembre de 2022 .
- Cosmo, ML y EC Lorenzini, " Tethers in Space Handbook " (3.ª ed.). Preparado para la NASA/MSFC por el Observatorio Astrofísico Smithsoniano, Cambridge, MA, diciembre de 1997. ( PDF )
- Estes, RD; Lorenzini, EC; Sanmartín, JR; Martinez-Sanchez, M.; Savich, NA (diciembre de 1995). "Nuevos anclajes de alta corriente: ¿una fuente de energía viable para la estación espacial? Un libro blanco" (PDF) . Archivado desde el original (PDF) el 18 de febrero de 2006.
- Savich, NA; Sanmartín, JR (1994). "Correa electrodinámica corta de alta corriente". Proc. Int. Mesa redonda sobre correas en el espacio . pág. 417.
- McCoy, James E.; et al. (abril de 1995). "Resultados del experimento de vuelo con motor-generador de plasma (PMG)". Actas de la 4.ª conferencia internacional sobre amarres en el espacio . Washington DC. págs. 57–84.
- Otros artículos
- " Ataduras electrodinámicas Archivado el 17 de mayo de 2011 en Wayback Machine . Tethers.com.
- " Sistema de anclaje electrodinámico de lanzadera (SETS) ".
- Enrico Lorenzini y Juan Sanmartín, " Ataduras electrodinámicas en el espacio: explotando leyes físicas fundamentales, las ataduras pueden proporcionar energía eléctrica de bajo costo, resistencia, empuje y gravedad artificial para los vuelos espaciales ". Scientific American, agosto de 2004.
- " Ataduras ". Guía de estudio de astronomía, BookRags.
- David P. Stern, " El experimento del anclaje espacial ". 25 de noviembre de 2001.



















![{\displaystyle \Delta V_{tc}=\left[{\frac {\eta \cdot I_{t}}{\rho }}\right]^{2/3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/931b24458ba4aeea5700e8321ee49da84aa2315d)



