Matroide orientado

Un matroide orientado es una estructura matemática que abstrae las propiedades de los gráficos dirigidos , los arreglos vectoriales sobre campos ordenados y los arreglos de hiperplanos sobre campos ordenados . ^{[1] En comparación, un} matroide ordinario (es decir, no orientado) abstrae las propiedades de dependencia que son comunes tanto a los gráficos , que no son necesariamente dirigidos , como a los arreglos de vectores sobre campos , que no son necesariamente ordenados . ^{[2] [3]}

Todas las matroides orientadas tienen una matroide subyacente . Por lo tanto, los resultados obtenidos en las matroides ordinarias se pueden aplicar a las matroides orientadas. Sin embargo, lo contrario es falso; algunas matroides no pueden convertirse en una matroide orientada orientando una estructura subyacente (por ejemplo, circuitos o conjuntos independientes). ^[4] La distinción entre matroides y matroides orientadas se analiza más adelante.

Los matroides suelen ser útiles en áreas como la teoría de dimensiones y los algoritmos . Debido a que un matroide orientado incluye detalles adicionales sobre la naturaleza orientada de una estructura, su utilidad se extiende a otras áreas, como la geometría y la optimización .

La primera aparición de matroides orientadas fue en un artículo de 1966 de George J. Minty y se limitó a matroides regulares . ^[5]

Posteriormente, RT Rockefellar (1969) planteó el problema de generalizar el concepto de Minty a espacios vectoriales reales. Su propuesta contribuyó al desarrollo de la teoría general.

Para abstraer el concepto de orientación en los bordes de un grafo a conjuntos, se necesita la capacidad de asignar "dirección" a los elementos de un conjunto. La forma de lograrlo es con la siguiente definición de conjuntos con signo .

• Un conjunto con signo , , combina un conjunto de objetos, , con una bipartición ordenada de ese conjunto en dos subconjuntos disjuntos: y .${\estilo de visualización X}$${\displaystyle {\underline {X}}}$ ${\displaystyle (X^{+},X^{-})}$${\estilo de visualización X^{+}}$${\estilo de visualización X^{-}}$

Los miembros de se llaman elementos positivos ; los miembros de son los elementos negativos .${\estilo de visualización X^{+}}$${\estilo de visualización X^{-}}$

• El conjunto se llama soporte de .${\displaystyle {\underline {X}}=X^{+}\cup X^{-}}$${\estilo de visualización X}$
• El conjunto vacío con signo , , se define como el conjunto vacío combinado con una bipartición (ordenada) del mismo en dos conjuntos vacíos: y .${\displaystyle \conjunto vacío}$${\displaystyle {\underline {\conjunto vacío}}}$${\displaystyle \conjunto vacío ^{+}}$${\displaystyle \conjunto vacío ^{-}}$
• El conjunto con signo es el opuesto de , escrito , si y${\estilo de visualización Y}$${\estilo de visualización X}$${\displaystyle Y=-X}$${\displaystyle Y^{+}=X^{-}}$${\displaystyle Y^{-}=X^{+}.}$

Dado un elemento del soporte, escribiremos para un elemento positivo y para un elemento negativo. De esta manera, un conjunto con signo simplemente suma signos negativos a elementos distinguidos. Esto tendrá sentido como una "dirección" solo cuando consideremos orientaciones de estructuras más grandes. Entonces, el signo de cada elemento codificará su dirección relativa a esta orientación.${\estilo de visualización x}$${\estilo de visualización x}$${\estilo de visualización -x}$

Al igual que los matroides ordinarios, existen varios sistemas equivalentes de axiomas . (Las estructuras que poseen múltiples axiomatizaciones equivalentes se denominan criptomórficas ).

Sea cualquier conjunto. Lo llamaremos conjunto base . Sea una colección de conjuntos con signo , cada uno de los cuales está respaldado por un subconjunto de . Si los siguientes axiomas son válidos para , entonces, equivalentemente, es el conjunto de circuitos con signo para un matroide orientado en .${\estilo de visualización E}$${\estilo de visualización E}$${\displaystyle {\mathcal {C}}}$${\estilo de visualización E}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$${\estilo de visualización E}$

• (C0)${\displaystyle \emptyset \notin {\mathcal {C}}}$
• (C1) (simétrico)${\displaystyle {\text{Para todo }}X\in {\mathcal {C}},~-\!X\in {\mathcal {C}}.}$
• (C2) (incomparable)${\displaystyle {\text{ Para todos }}X,Y\in {\mathcal {C}},~~{\text{ si }}{\underline {X}}\subseteq {\underline {Y}}{\text{ entonces }}(X=Y{\text{ o }}X=-Y).}$
• (C3) (eliminación débil)${\displaystyle {\text{ For all }}X,Y\in {\mathcal {C}},X\neq -Y{\text{ with an }}e\in X^{+}\cap Y^{-}{\text{ there is a }}Z\in {\mathcal {C}}{\text{ such that }}}$
  • ${\displaystyle Z^{+}\subseteq (X^{+}\cup Y^{+})\setminus \{e\}{\text{ and }}}$
  • ${\displaystyle Z^{-}\subseteq (X^{-}\cup Y^{-})\setminus \{e\}.}$

La composición de los conjuntos con signo y es el conjunto con signo definido por , , y . Los vectores de un matroide orientado son las composiciones de circuitos. Los vectores de un matroide orientado satisfacen los siguientes axiomas:${\displaystyle X}$${\displaystyle Y}$${\displaystyle X\circ Y}$${\displaystyle {\underline {X\circ Y}}={\underline {X}}\cup {\underline {Y}}}$${\displaystyle (X\circ Y)^{+}=X^{+}\cup \left(Y^{+}\setminus X^{-}\right)}$${\displaystyle (X\circ Y)^{-}=X^{-}\cup \left(Y^{-}\setminus X^{+}\right)}$${\displaystyle {\mathcal {V}}}$

• ${\displaystyle \emptyset \in {\mathcal {V}}}$
• ${\displaystyle {\mathcal {V}}=-{\mathcal {V}}}$
• Para todos ,${\displaystyle X,Y\in {\mathcal {V}}}$${\displaystyle X\circ Y\in {\mathcal {V}}}$
• para todo , y , existe un , tal que${\displaystyle X,Y\in {\mathcal {V}}}$${\displaystyle e\in X^{+}\cap Y^{-}}$${\displaystyle f\in ({\underline {X}}\setminus {\underline {Y}})\cup ({\underline {Y}}\setminus {\underline {X}})\cup (X^{+}\cap Y^{+})\cup (X^{-}\cap Y^{-})}$${\displaystyle Z\in {\mathcal {V}}}$
  • ${\displaystyle Z^{+}\subset X^{+}\cup Y^{+}\setminus e}$,
  • ${\displaystyle Z^{-}\subset X^{-}\cup Y^{-}\setminus e}$, y
  • ${\displaystyle f\in {\underline {Z}}}$.

Los covectores de un matroide orientado son los vectores de su matroide orientado dual.

Sea como se indica arriba. Para cada entero no negativo , un quirótopo de rango es una función que satisface los siguientes axiomas:${\displaystyle E}$${\displaystyle r}$${\displaystyle r}$${\displaystyle \chi \colon E^{r}\to \{-1,0,1\}}$

• (B0) (no trivial) : no es idénticamente cero${\displaystyle \chi }$
• (B1) (alternando) : Para cualquier permutación y , , donde es el signo de la permutación.${\displaystyle \sigma }$${\displaystyle x_{1},\dots ,x_{r}\in E}$${\displaystyle \chi \left(x_{\sigma (1)},\dots ,x_{\sigma (r)}\right)=\operatorname {sgn} (\sigma )\chi \left(x_{1},\dots ,x_{r}\right)}$${\displaystyle \operatorname {sgn} (\sigma )}$
• (B2) (intercambio) : Para cualquier tal que para cada , entonces también tenemos .${\displaystyle x_{1},\dots ,x_{r},y_{1},\dots ,y_{r}\in E}$${\displaystyle \chi (y_{i},x_{2},\dots ,x_{r})\chi (y_{1},\dots ,y_{i-1},x_{1},y_{i+1},\dots ,y_{r})\geq 0}$${\displaystyle i}$${\displaystyle \chi \left(x_{1},\dots ,x_{r}\right)\chi \left(y_{1},\dots ,y_{r}\right)\geq 0}$

El término quirótopo se deriva de la noción matemática de quiralidad , que es un concepto abstraído de la química , donde se utiliza para distinguir moléculas que tienen la misma estructura excepto por una reflexión.

Cada quirótopo de rango da lugar a un conjunto de bases de un matroide que consiste en aquellos subconjuntos de elementos que asignan un valor distinto de cero. ^[6] El quirótopo puede entonces firmar los circuitos de ese matroide. Si es un circuito del matroide descrito, entonces donde es una base. Entonces puede firmarse con elementos positivos .${\displaystyle r}$${\displaystyle E}$${\displaystyle r}$${\displaystyle \chi }$${\displaystyle C}$${\displaystyle C\subset \{x_{1},\dots ,x_{r},x_{r+1}\}}$${\displaystyle \{x_{1},\dots ,x_{r}\}}$${\displaystyle C}$

${\displaystyle C^{+}=\{x_{i}:(-1)^{i}\chi (x_{1},\dots ,x_{i-1},x_{i+1},\dots ,x_{r+1})=1\}}$

y los elementos negativos el complemento. Así, un quirótopo da lugar a las bases orientadas de un matroide orientado. En este sentido, (B0) es el axioma no vacío para bases y (B2) es la propiedad de intercambio de bases.

Las matroides orientadas se introducen a menudo (por ejemplo, Bachem y Kern) como una abstracción para grafos dirigidos o sistemas de inecuaciones lineales. A continuación se presentan las construcciones explícitas.

Dado un dígrafo , definimos un circuito con signo a partir del circuito estándar del grafo mediante el siguiente método. El soporte del circuito con signo es el conjunto estándar de aristas en un ciclo mínimo. Recorremos el ciclo en sentido horario o antihorario asignando aquellas aristas cuya orientación concuerda con la dirección a los elementos positivos y aquellas aristas cuya orientación no concuerda con la dirección a los elementos negativos . Si es el conjunto de todos tales , entonces es el conjunto de circuitos con signo de un matroide orientado sobre el conjunto de aristas del grafo dirigido.${\displaystyle \textstyle {\underline {X}}}$${\displaystyle \textstyle X^{+}}$${\displaystyle \textstyle X^{-}}$${\displaystyle \textstyle {\mathcal {C}}}$${\displaystyle \textstyle X}$${\displaystyle \textstyle {\mathcal {C}}}$

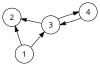
Si consideramos el grafo dirigido de la derecha, podemos ver que solo hay dos circuitos, a saber y . Luego, solo hay cuatro circuitos con signo posibles correspondientes a orientaciones en sentido horario y antihorario, a saber , , , y . Estos cuatro conjuntos forman el conjunto de circuitos con signo de un matroide orientado en el conjunto .${\displaystyle \textstyle \{(1,2),(1,3),(3,2)\}}$${\displaystyle \textstyle \{(3,4),(4,3)\}}$${\displaystyle \textstyle \{(1,2),-(1,3),-(3,2)\}}$${\displaystyle \textstyle \{-(1,2),(1,3),(3,2)\}}$${\displaystyle \textstyle \{(3,4),(4,3)\}}$${\displaystyle \textstyle \{-(3,4),-(4,3)\}}$${\displaystyle \textstyle \{(1,2),(1,3),(3,2),(3,4),(4,3)\}}$

Si es cualquier subconjunto finito de , entonces el conjunto de conjuntos linealmente dependientes mínimos forma el conjunto de circuitos de un matroide en . Para extender esta construcción a los matroides orientados, para cada circuito existe una dependencia lineal mínima${\displaystyle \textstyle E}$${\displaystyle \textstyle \mathbb {R} ^{n}}$${\displaystyle \textstyle E}$${\displaystyle \textstyle \{v_{1},\dots ,v_{m}\}}$

${\displaystyle \sum _{i=1}^{m}\lambda _{i}v_{i}=0}$

con . Entonces el circuito con signo tiene elementos positivos y elementos negativos . El conjunto de todos ellos forma el conjunto de circuitos con signo de un matroide orientado en . Los matroides orientados que se pueden realizar de esta manera se denominan representables .${\displaystyle \textstyle \lambda _{i}\in \mathbb {R} }$${\displaystyle \textstyle X=\{X^{+},X^{-}\}}$${\displaystyle \textstyle X^{+}=\{v_{i}:\lambda _{i}>0\}}$${\displaystyle \textstyle X^{-}=\{v_{i}:\lambda _{i}<0\}}$${\displaystyle \textstyle X}$${\displaystyle \textstyle E}$

Dado el mismo conjunto de vectores , podemos definir el mismo matroide orientado con un quirótopo . Para cualquier let${\displaystyle E}$${\displaystyle \chi :E^{r}\rightarrow \{-1,0,1\}}$${\displaystyle x_{1},\dots ,x_{r}\in E}$

${\displaystyle \chi (x_{1},\dots ,x_{r})=\operatorname {sgn} (\det(x_{1},\dots ,x_{r}))}$

donde el lado derecho de la ecuación es el signo del determinante . Entonces es el quirótopo del mismo matroide orientado en el conjunto .${\displaystyle \chi }$${\displaystyle E}$

Una disposición de hiperplanos real es un conjunto finito de hiperplanos en , cada uno de los cuales contiene el origen. Al elegir un lado de cada hiperplano como el lado positivo, obtenemos una disposición de semiespacios. Una disposición de semiespacios descompone el espacio ambiente en una colección finita de celdas, cada una definida por el lado de cada hiperplano en el que cae. Es decir, asigna cada punto al conjunto con signo si está en el lado positivo de y si está en el lado negativo de . Esta colección de conjuntos con signo define el conjunto de covectores del matroide orientado, que son los vectores del matroide orientado dual. ^[7]${\displaystyle {\mathcal {A}}=\{H_{1},\ldots ,H_{n}\}}$${\displaystyle \mathbb {R} ^{d}}$${\displaystyle x\in \mathbb {R} ^{d}}$${\displaystyle X=(X^{+},X^{-})}$${\displaystyle i\in X^{+}}$${\displaystyle x}$${\displaystyle H_{i}}$${\displaystyle i\in X^{-}}$${\displaystyle x}$${\displaystyle H_{i}}$

Günter M. Ziegler introduce matroides orientados a través de politopos convexos.

Un matroide estándar se llama orientable si sus circuitos son los soportes de circuitos con signo de algún matroide orientado. Se sabe que todos los matroides representables reales son orientables. También se sabe que la clase de matroides orientables está cerrada bajo la toma de menores , sin embargo se sabe que la lista de menores prohibidos para matroides orientables es infinita. ^[8] En este sentido, los matroides orientados son una formalización mucho más estricta que los matroides regulares.

Así como un matroide tiene duales únicos , un matroide orientado tiene un dual único, a menudo llamado su "dual ortogonal". Esto significa que los matroides subyacentes son duales y que los cocircuitos están signados de modo que son "ortogonales" a cada circuito. Se dice que dos conjuntos signados son ortogonales si la intersección de sus soportes está vacía o si la restricción de sus elementos positivos a la intersección y elementos negativos a la intersección forman dos conjuntos signados no idénticos y no opuestos. La existencia y unicidad del matroide orientado dual depende del hecho de que cada circuito signado es ortogonal a cada cocircuito signado. ^[9]

Para ver por qué la ortogonalidad es necesaria para la unicidad, basta con observar el ejemplo del dígrafo anterior. Sabemos que, en el caso de los grafos planares, el dual del matroide de circuito es el matroide de circuito del dual planar del grafo . Por lo tanto, hay tantos pares duales diferentes de matroides orientadas en función del matroide del grafo como formas de orientar el grafo y, de manera correspondiente, su dual.

Para ver la construcción explícita de este único matroide ortogonal dual orientado, considere el quirótopo de un matroide orientado . Si consideramos una lista de elementos de como una permutación cíclica, entonces definimos como el signo de la permutación asociada. Si se define como${\displaystyle \chi :E^{r}\rightarrow \{-1,0,1\}}$${\displaystyle x_{1},\dots ,x_{k}\in E}$${\displaystyle \operatorname {sgn} (x_{1},\dots ,x_{k})}$${\displaystyle \chi ^{*}:E^{|E|-r}\rightarrow \{-1,0,1\}}$

${\displaystyle \chi ^{*}(x_{1},\dots ,x_{r})\mapsto \chi (x_{r+1},\dots ,x_{|E|})\operatorname {sgn} (x_{1},\dots ,x_{r},x_{r+1},\dots ,x_{|E|}),}$

entonces es el quirótopo del único matroide ortogonal dual orientado. ^[10]${\displaystyle \chi ^{*}}$

No todos los matroides orientados son representables, es decir, no todos tienen realizaciones como configuraciones puntuales o, equivalentemente, disposiciones de hiperplano. Sin embargo, en cierto sentido, todos los matroides orientados se acercan a tener realizaciones como disposiciones de hiperplano. En particular, el teorema de representación topológica de Folkman-Lawrence establece que cualquier matroide orientado tiene una realización como una disposición de pseudoesferas . Una pseudoesfera -dimensional es una incrustación de tal que existe un homeomorfismo de modo que incrusta como un ecuador de . En este sentido, una pseudoesfera es simplemente una esfera domesticada (a diferencia de las esferas salvajes ). Una disposición de pseudoesferas en es una colección de pseudoesferas que se intersecan a lo largo de pseudoesferas. Finalmente, el teorema de representación topológica de Folkman-Lawrence establece que cada matroide orientado de rango puede obtenerse a partir de una disposición de pseudoesferas en . ^[11] Lleva el nombre de Jon Folkman y Jim Lawrence, quienes lo publicaron en 1978.${\displaystyle d}$${\displaystyle e:S^{d}\hookrightarrow S^{d+1}}$${\displaystyle h:S^{d+1}\rightarrow S^{d+1}}$${\displaystyle h\circ e}$${\displaystyle S^{d}}$${\displaystyle S^{d+1}}$${\displaystyle S^{d}}$${\displaystyle d+1}$${\displaystyle S^{d}}$

La teoría de matroides orientadas ha influido en el desarrollo de la geometría combinatoria , especialmente la teoría de politopos convexos , zonotopos y configuraciones de vectores (equivalentemente, disposiciones de hiperplanos ). ^[12] Muchos resultados (el teorema de Carathéodory , el teorema de Helly , el teorema de Radon , el teorema de Hahn-Banach , el teorema de Kerin-Milman , el lema de Farkas ) pueden formularse utilizando matroides orientadas apropiadas. ^[13]

El desarrollo de un sistema axiomático para matroides orientadas fue iniciado por R. Tyrrell Rockafellar para describir los patrones de signos de las matrices que surgen a través de las operaciones de pivoteo del algoritmo simplex de Dantzig; Rockafellar se inspiró en los estudios de Albert W. Tucker sobre dichos patrones de signos en "Tucker tableaux". ^[14]

La teoría de matroides orientados ha llevado a grandes avances en la optimización combinatoria . En programación lineal , fue el lenguaje en el que Robert G. Bland formuló su regla de pivote , por la cual el algoritmo símplex evita los ciclos. De manera similar, Terlaky y Zhang la utilizaron para demostrar que sus algoritmos entrecruzados tienen terminación finita para problemas de programación lineal . Todd y Terlaky obtuvieron resultados similares en programación cuadrática convexa. ^[15] Se ha aplicado a la programación lineal-fraccional , ^{[16] a problemas} de programación cuadrática y a problemas de complementariedad lineal . ^{[17] [18] [19]}

Fuera de la optimización combinatoria , la teoría matroide orientada también aparece en la minimización convexa en la teoría de "programación monotrópica" de Rockafellar y nociones relacionadas de "descenso fortificado". ^[20] De manera similar, la teoría matroide ha influido en el desarrollo de algoritmos combinatorios, particularmente el algoritmo greedy . ^[21] De manera más general, un greedoide es útil para estudiar la terminación finita de algoritmos.

• Bachem, Achim; Kern, Walter (1992). Dualidad de programación lineal: una introducción a las matroides orientadas . Universitext. Springer-Verlag. doi :10.1007/978-3-642-58152-6. ISBN 978-3-540-55417-2.Señor 1230380  .
• Björner, Anders ; Las Vergnas, Michel ; Sturmfels, Bernd ; White, Neil; Ziegler, Günter (1999). Matroides orientadas . Enciclopedia de matemáticas y sus aplicaciones. Vol. 46 (2.ª ed.). Cambridge University Press . ISBN 978-0-521-77750-6.Zbl 0944.52006  .
• Bokowski, Jürgen (2006). Matroides orientados a la computación. Clases de equivalencia de matrices dentro de un marco natural . Cambridge University Press . ISBN 978-0-521-84930-2.Zbl 1120.52011  .
• Lawler, Eugene (2001). Optimización combinatoria: redes y matroides . Dover. ISBN 978-0-486-41453-9.Zbl 1058.90057  .
• Evar D. Nering y Albert W. Tucker , 1993, Programas lineales y problemas relacionados , Academic Press. (primaria)
• Rockafellar, R. Tyrrell (1984). Flujos de red y optimización monotrópica . Wiley-Interscience.republicado por Athena Scientific de Dimitri Bertsekas , 1998.
• Ziegler, Günter M. (1994). Lecciones sobre politopos . Nueva York: Springer-Verlag.
• Richter-Gebert, Jürgen; Ziegler, Günter M. (1997). "Matroides orientadas". En Goodman, Jacob E .; O'Rourke, Joseph (eds.). Manual de geometría discreta y computacional . Boca Ratón: CRC Press. págs. 111-132. ISBN 9780849385247.

• A. Bachem, A. Wanka, Teoremas de separación para matroides orientadas, Discrete Math. 70 (1988) 303–310.
• Bland, Robert G. (1977). "Nuevas reglas de pivoteo finito para el método símplex". Matemáticas de la investigación de operaciones . 2 (2): 103–107. doi :10.1287/moor.2.2.103.
• Folkman, Jon ; Lawrence, Jim (octubre de 1978). "Matroides orientados". Revista de teoría combinatoria . Serie B. 25 (2): 199–236. doi : 10.1016/0095-8956(78)90039-4 .
• Fukuda, Komei ; Terlaky, Tamás (1997). Thomas M. Liebling; Dominique de Werra (eds.). "Métodos entrecruzados: una nueva visión de los algoritmos pivote" (PDF) . Programación matemática, serie B . 79 (1–3). Ámsterdam: North-Holland Publishing Co.: 369–395. doi :10.1007/BF02614325. MR  1464775. S2CID  2794181.
• Fukuda, Komei ; Namiki, Makoto (marzo de 1994). "Sobre los comportamientos extremos del método del índice mínimo de Murty". Programación matemática . 64 (1): 365–370. doi :10.1007/BF01582581. MR  1286455. S2CID  21476636.
• Illés, Tibor; Szirmai, Ákos; Terlaky, Tamás (1999). "El método entrecruzado finito para la programación hiperbólica". Revista europea de investigación operativa . 114 (1): 198–214. CiteSeerX  10.1.1.36.7090 . doi :10.1016/S0377-2217(98)00049-6. ISSN  0377-2217.
• R. Tyrrell Rockafellar (1969). Los vectores elementales de un subespacio de , en Combinatorial Mathematics and its Applications , RC Bose y TA Dowling (eds.), Univ. of North Carolina Press, págs. 104–127.${\displaystyle R^{n}}$
• Roos, C. (1990). "Un ejemplo exponencial de la regla de pivote de Terlaky para el método símplex entrecruzado". Programación matemática . Serie A. 46 (1): 79–84. doi :10.1007/BF01585729. MR  1045573. S2CID  33463483.
• Terlaky, T. (1985). "Un método de cruce convergente". Optimización: una revista de programación matemática e investigación de operaciones . 16 (5): 683–690. doi :10.1080/02331938508843067. ISSN  0233-1934. MR  0798939.
• Terlaky, Tamás (1987). "Un método de entrecruzamiento finito para matroides orientados". Journal of Combinatorial Theory . Serie B. 42 (3): 319–327. doi : 10.1016/0095-8956(87)90049-9 . ISSN  0095-8956. MR  0888684.
• Terlaky, Tamás; Zhang, Shu Zhong (1993). "Reglas de pivote para programación lineal: una encuesta sobre desarrollos teóricos recientes". Anales de investigación de operaciones . 46–47 (1): 203–233. CiteSeerX  10.1.1.36.7658 . doi :10.1007/BF02096264. ISSN  0254-5330. MR  1260019. S2CID  6058077.
• Todd, Michael J. (1985). "Programación lineal y cuadrática en matroides orientados". Journal of Combinatorial Theory . Serie B. 39 (2): 105–133. doi : 10.1016/0095-8956(85)90042-5 .
• Wang, Zhe Min (1987). "Un algoritmo libre de eliminación conforme finita sobre programación matroide orientada". Anales chinos de matemáticas (Shuxue Niankan B Ji) . Serie B. 8 (1): 120–125. ISSN  0252-9599. MR  0886756.

• Ziegler, Günter (1998). "Matroides orientadas hoy". The Electronic Journal of Combinatorics : DS4: 10 de septiembre de 1998. doi :10.37236/25.
• Malkevitch, Joseph. "Matroides orientadas: el poder de la unificación". Columna destacada . American Mathematical Society . Consultado el 14 de septiembre de 2009 .

• Komei Fukuda (ETH Zentrum, Zurich) con publicaciones que incluyen Programación matroide orientada (tesis doctoral de 1982)
• Tamás Terlaky (Lehigh University) con publicaciones