Mapeo de árboles
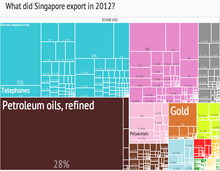
Método de visualización de datos jerárquicos
Mapa de árbol de las exportaciones de Singapur por categoría de producto, 2012. Los mapas de árbol de exportaciones de productos son una de las aplicaciones más recientes de este tipo de visualizaciones, desarrolladas por el Observatorio de Complejidad Económica de Harvard-MIT .

En visualización de información y computación , la representación en árbol es un método para mostrar datos jerárquicos utilizando figuras anidadas , generalmente rectángulos.

Los mapas de árbol muestran datos jerárquicos ( estructurados en árbol ) como un conjunto de rectángulos anidados. A cada rama del árbol se le asigna un rectángulo, que luego se cubre con rectángulos más pequeños que representan subramas. El rectángulo de un nodo hoja tiene un área proporcional a una dimensión específica de los datos . [1] A menudo, los nodos hoja se colorean para mostrar una dimensión separada de los datos.

Cuando las dimensiones de color y tamaño se correlacionan de alguna manera con la estructura del árbol, a menudo se pueden ver fácilmente patrones que serían difíciles de detectar de otras maneras, como por ejemplo si un determinado color es particularmente relevante. Una segunda ventaja de los mapas de árbol es que, por su construcción, hacen un uso eficiente del espacio. Como resultado, pueden mostrar de forma legible miles de elementos en la pantalla simultáneamente.

Algoritmos de mosaico

Para crear un mapa de árbol, se debe definir un algoritmo de teselado , es decir, una forma de dividir una región en subregiones de áreas específicas. Idealmente, un algoritmo de mapa de árbol crearía regiones que satisfagan los siguientes criterios:

  1. Una relación de aspecto pequeña , idealmente cercana a uno. Las regiones con una relación de aspecto pequeña (es decir, los objetos gordos ) son más fáciles de percibir. [2]
  2. Conservar cierto sentido del orden en los datos de entrada (ordenados).
  3. Cambiar para reflejar los cambios en los datos subyacentes (alta estabilidad).

Estas propiedades tienen una relación inversa. A medida que se optimiza la relación de aspecto, el orden de colocación se vuelve menos predecible. A medida que el orden se vuelve más estable, la relación de aspecto se degrada. [ ejemplo necesario ]

Mapas de árboles rectangulares

Hasta la fecha, se han desarrollado quince algoritmos primarios de mapas de árboles rectangulares:

Algoritmos de mapas de árboles [3]
AlgoritmoOrdenRelaciones de aspectoEstabilidad
Árbol binarioparcialmente ordenadoaltoestable
Cortar y trocear [4]ordenadomuy altoestable
Tira [5]ordenadomedioestabilidad media
Pivote por el medio [6]ordenadomedioestabilidad media
Pivote por división [6]ordenadomediobaja estabilidad
Pivote por tamaño [6]ordenadomedioestabilidad media
Dividir [7]ordenadomedioestabilidad media
Espiral [8]ordenadomedioestabilidad media
Hilbert [9]ordenadomedioestabilidad media
Moore [9]ordenadomedioestabilidad media
Cuadrado [10]ordenadobajobaja estabilidad
Mapas de árboles mixtos [11]desordenadobajoestabilidad media
Aproximación [12]desordenadobajoestabilidad media
Git [13]desordenadomedioestable
Movimientos locales [14]desordenadomedioestable

Mapas de árboles convexos

Los mapas de árbol rectangulares tienen la desventaja de que su relación de aspecto puede ser arbitrariamente alta en el peor de los casos. Como ejemplo simple, si la raíz del árbol tiene solo dos hijos, uno con peso y otro con peso , entonces la relación de aspecto del hijo más pequeño será , que puede ser arbitrariamente alta. Para hacer frente a este problema, se han propuesto varios algoritmos que utilizan regiones que son polígonos convexos generales , no necesariamente rectangulares. 1 / norte {\estilo de visualización 1/n} 1 − 1 / norte {\estilo de visualización 1-1/n} norte {\estilo de visualización n}

Los mapas de árbol convexos se desarrollaron en varios pasos; cada paso mejoró el límite superior de la relación de aspecto. Los límites se dan como una función de: - el número total de nodos en el árbol y - la profundidad total del árbol. norte {\estilo de visualización n} d {\estilo de visualización d}

  1. Onak y Sidiropoulos [15] demostraron un límite superior de . Oh ( ( d registro ⁡ norte ) 17 ) {\displaystyle O((d\log {n})^{17})}
  2. De-Berg y Onak y Sidiropoulos [16] mejoran el límite superior a , y prueban un límite inferior de . Oh ( d + registro ⁡ norte ) {\displaystyle O(d+\log {n})} Oh ( d ) {\displaystyle O(d)}
  3. De-Berg y Speckmann y van-der-Weele [17] mejoran el límite superior a , coincidiendo con el límite inferior teórico. (Para el caso especial donde la profundidad es 1, presentan un algoritmo que utiliza solo cuatro clases de polígonos de 45 grados (rectángulos, triángulos rectángulos, trapecios rectángulos y pentágonos de 45 grados), y garantiza una relación de aspecto de como máximo 34/7). Oh ( d ) {\displaystyle O(d)}

Los dos últimos algoritmos funcionan en dos pasos (muy simplificados para mayor claridad):

  1. El árbol original se convierte en un árbol binario: cada nodo con más de dos hijos se reemplaza por un subárbol en el que cada nodo tiene exactamente dos hijos.
  2. Cada región que representa un nodo (empezando por la raíz) se divide en dos, utilizando una línea que mantiene los ángulos entre las aristas lo más grandes posible. Es posible demostrar que, si todas las aristas de un polígono convexo están separadas por un ángulo de al menos , entonces su relación de aspecto es . Es posible asegurar que, en un árbol de profundidad , el ángulo se divide por un factor de como máximo , de ahí la garantía de la relación de aspecto. ϕ {\estilo de visualización \phi} Oh ( 1 / ϕ ) {\displaystyle O(1/\phi )} d {\estilo de visualización d} d {\estilo de visualización d}

Mapas de árboles ortoconvexos

En los mapas de árbol convexos, la relación de aspecto no puede ser constante, sino que aumenta con la profundidad del árbol. Para lograr una relación de aspecto constante, se pueden utilizar mapas de árbol ortoconvexos [17] . En ellos, todas las regiones son polígonos rectilíneos ortoconvexos con una relación de aspecto de 64 como máximo; y las hojas son rectángulos con una relación de aspecto de 8 como máximo, o bien tienen forma de L o de S con una relación de aspecto de 32 como máximo.

Para el caso especial donde la profundidad es 1, presentan un algoritmo que utiliza solo rectángulos y formas de L, y la relación de aspecto es como máximo ; los nodos internos utilizan solo rectángulos con relación de aspecto como máximo . 2 + 2 / 3 ≈ 3.15 {\displaystyle 2+2/{\sqrt {3}}\aproximadamente 3,15} 1 + 3 ≈ 2.73 {\displaystyle 1+{\sqrt {3}}\aproximadamente 2,73}

Otros mapas de árboles

Mapas de árboles de Voronoi
[18] Basado en cálculos de diagramas de Voronoi . El algoritmo es iterativo y no proporciona ningún límite superior para la relación de aspecto.
Mapas de árboles en formato rompecabezas [19]
Basados ​​en la geometría de curvas que llenan el espacio, se supone que los pesos son números enteros y que su suma es un número cuadrado. Las regiones del mapa son polígonos rectilíneos y altamente no ortoconvexos. Se garantiza que su relación de aspecto sea como máximo de 4.
Mapas de Gosper
[20] Basado en la geometría de las curvas de Gosper , es ordenado y estable, pero tiene una relación de aspecto muy alta.

Historia

Uso del espacio del disco duro visualizado en TreeSize, software lanzado por primera vez en 1996

Las visualizaciones basadas en áreas existen desde hace décadas. Por ejemplo, los gráficos de mosaico (también conocidos como diagramas de Marimekko) utilizan teselas rectangulares para mostrar distribuciones conjuntas (es decir, lo más común es que sean esencialmente gráficos de columnas apiladas donde las columnas tienen diferentes anchos). Sin embargo, la característica distintiva principal de un mapa de árbol es la construcción recursiva que le permite extenderse a datos jerárquicos con cualquier número de niveles. Esta idea fue inventada por el profesor Ben Shneiderman en el Laboratorio de Interacción Humano-Computadora de la Universidad de Maryland a principios de los años 1990. [21] [22] Shneiderman y sus colaboradores luego profundizaron la idea al introducir una variedad de técnicas interactivas para filtrar y ajustar los mapas de árbol.

Todos estos primeros mapas de árbol utilizaban el sencillo algoritmo de mosaico de "corte y división". A pesar de muchas propiedades deseables (es estable, conserva el orden y es fácil de implementar), el método de corte y división a menudo produce mosaicos con muchos rectángulos largos y delgados. En 1994, Mountaz Hascoet y Michel Beaudouin-Lafon inventaron un algoritmo de "cuadrado", popularizado posteriormente por Jarke van Wijk , que creaba mosaicos cuyos rectángulos eran más cercanos al cuadrado. En 1999, Martin Wattenberg utilizó una variación del algoritmo de "cuadrado" que llamó "pivot and slice" para crear el primer mapa de árbol basado en la Web, el SmartMoney Map of the Market, que mostraba datos sobre cientos de empresas del mercado de valores de Estados Unidos. Tras su lanzamiento, los mapas de árbol disfrutaron de un gran interés, especialmente en contextos financieros. [ cita requerida ]

Una tercera ola de innovación en mapas de árboles se produjo alrededor de 2004, después de que Marcos Weskamp creara Newsmap, un mapa de árboles que mostraba titulares de noticias. Este ejemplo de un mapa de árboles no analítico inspiró a muchos imitadores e introdujo los mapas de árboles a una audiencia nueva y amplia. [ cita requerida ] En los últimos años, los mapas de árboles se han abierto camino en los medios de comunicación tradicionales, incluido el uso por parte del New York Times. [23] [24] El Treemap Art Project [25] produjo 12 imágenes enmarcadas para las Academias Nacionales (Estados Unidos) , se mostró en la exhibición Every AlgoRiThm has ART in It [26] en Washington, DC y otro conjunto para la colección del Museo de Arte Moderno de Nueva York.

Véase también

Referencias

  1. ^ Li, Rita Yi Man; Chau, Kwong Wing; Zeng, Frankie Fanjie (2019). "Ranking de riesgos para obras de construcción existentes y nuevas". Sustainability . 11 (10): 2863. doi : 10.3390/su11102863 .
  2. ^ Kong, N; Heer, J; Agrawala, M (2010). "Pautas perceptivas para la creación de mapas de árbol rectangulares". IEEE Transactions on Visualization and Computer Graphics . 16 (6): 990–8. CiteSeerX 10.1.1.688.4140 . doi :10.1109/TVCG.2010.186. PMID  20975136. S2CID  11597084. 
  3. ^ Vernier, E.; Sondag, M.; Comba, J.; Speckmann, B.; Telea, A.; Verbeek, K. (2020). "Comparación cuantitativa de mapas de árbol dependientes del tiempo". Computer Graphics Forum . 39 (3): 393–404. arXiv : 1906.06014 . doi :10.1111/cgf.13989. S2CID  189898065.
  4. ^ Shneiderman, Ben (2001). "Diseños de mapas de árbol ordenados" (PDF) . Infovis : 73.
  5. ^ Benjamin, Bederson; Shneiderman, Ben; Wattenberg, Martin (2002). "Mapa de árbol ordenado y cuántico: Cómo hacer un uso eficaz del espacio 2D para mostrar jerarquías" (PDF) . ACM Transactions on Graphics . 21 (4): 833–854. CiteSeerX 10.1.1.145.2634 . doi :10.1145/571647.571649. S2CID  7253456. 
  6. ^ abc Shneiderman, Ben; Wattenberg, Martin (2001). "Diseños de mapas de árbol ordenados". Simposio IEEE sobre visualización de información : 73–78.
  7. ^ Engdahl, Björn. Mapas de árboles ordenados y cuánticos: Cómo hacer un uso eficaz del espacio 2D para mostrar jerarquías .
  8. ^ Tu, Y.; Shen, H. (2007). "Visualización de cambios de datos jerárquicos mediante mapas de árbol" (PDF) . IEEE Transactions on Visualization and Computer Graphics . 13 (6): 1286–1293. doi :10.1109/TVCG.2007.70529. PMID  17968076. S2CID 14206074 . Archivado (PDF) desde el original el 8 de agosto de 2022. 
  9. ^ ab Tak, S.; Cockburn, A. (2013). "Estabilidad espacial mejorada con mapas de árboles de Hilbert y Moore" (PDF) . IEEE Transactions on Visualization and Computer Graphics . 19 (1): 141–148. doi :10.1109/TVCG.2012.108. PMID  22508907. S2CID  6099935.
  10. ^ Bruls, Mark; Huizing, Kees; van Wijk, Jarke J. (2000). "Mapas de árboles cuadriculados". En de Leeuw, W.; van Liere, R. (eds.). Visualización de datos 2000: Proc. Simposio conjunto de Eurographics e IEEE TCVG. sobre visualización (PDF) . Springer-Verlag. págs. 33–42..
  11. ^ Roël Vliegen; Erik-Jan van der Linden; Jarke J. van Wijk . "Visualización de datos empresariales con mapas de árbol generalizados" (PDF) . Archivado desde el original (PDF) el 24 de julio de 2011 . Consultado el 24 de febrero de 2010 .
  12. ^ Nagamochi, H.; Abe, Y.; Wattenberg, Martin (2007). "Un algoritmo de aproximación para diseccionar un rectángulo en rectángulos con áreas específicas". Matemáticas Aplicadas Discretas . 155 (4): 523–537. doi : 10.1016/j.dam.2006.08.005 .
  13. ^ Vernier, E.; Comba, J.; Telea, A. (2018). "Comparación cuantitativa de mapas de árbol dinámicos para la visualización de la evolución del software". Conferencia sobre visualización de software : 99–106.
  14. ^ Sondag, M.; Speckmann, B.; Verbeek, K. (2018). "Mapa de árbol estable mediante movimientos locales". IEEE Transactions on Visualization and Computer Graphics . 24 (1): 729–738. doi :10.1109/TVCG.2017.2745140. PMID  28866573. S2CID  27739774.
  15. ^ Krzysztof Onak; Anastasios Sidiropoulos. "Particiones circulares con aplicaciones para visualización e incrustaciones" . Consultado el 26 de junio de 2011 .
  16. ^ Mark de Berg; Onak, Krzysztof; Sidiropoulos, Anastasios (2013). "Particiones poligonales gruesas con aplicaciones para visualización e incrustaciones". Journal of Computational Geometry . 4 (1): 212–239. arXiv : 1009.1866 .
  17. ^ ab De Berg, Mark; Speckmann, Bettina ; Van Der Weele, Vincent (2014). "Mapas de árboles con relación de aspecto limitada". Geometría computacional . 47 (6): 683. arXiv : 1012.1749 . doi : 10.1016/j.comgeo.2013.12.008 . S2CID  12973376.Versión de conferencia: Mapas de árboles convexos con relación de aspecto limitada (PDF) . EuroCG. 2011.
  18. ^ Balzer, Michael; Deussen, Oliver (2005). "Voronoi Treemaps". En Stasko, John T.; Ward, Matthew O. (eds.). Simposio IEEE sobre visualización de información (InfoVis 2005), 23-25 ​​de octubre de 2005, Minneapolis, MN, EE. UU. (PDF) . IEEE Computer Society. pág. 7..
  19. ^ Wattenberg, Martin (2005). "Una nota sobre visualizaciones que llenan el espacio y curvas que llenan el espacio". En Stasko, John T.; Ward, Matthew O. (eds.). Simposio IEEE sobre visualización de información (InfoVis 2005), 23-25 ​​de octubre de 2005, Minneapolis, MN, EE. UU. (PDF) . IEEE Computer Society. pág. 24..
  20. ^ Auber, David; Huet, Carlos; Lamberto, Antoine; Renoust, Benjamín; Sallaberry, Arnaud; Saulnier, Agnès (2013). "Mapa de Gosper: uso de una curva de Gosper para diseñar datos jerárquicos". Transacciones IEEE sobre visualización y gráficos por computadora . 19 (11): 1820–1832. doi :10.1109/TVCG.2013.91. PMID  24029903. S2CID  15050386..
  21. ^ Shneiderman, Ben (1992). "Visualización de árboles con mapas de árboles: enfoque de relleno de espacio en 2D". ACM Transactions on Graphics . 11 : 92–99. doi :10.1145/102377.115768. hdl : 1903/367 . S2CID  1369287.
  22. ^ Ben Shneiderman ; Catherine Plaisant (25 de junio de 2009). "Mapas de árbol para la visualización de jerarquías con restricciones espaciales ~ Incluyendo la historia de la investigación de mapas de árbol en la Universidad de Maryland" . Consultado el 23 de febrero de 2010 .
  23. ^ Cox, Amanda; Fairfield, Hannah (25 de febrero de 2007). "La salud del mercado de automóviles, furgonetas, todoterrenos y camiones". The New York Times . Consultado el 12 de marzo de 2010 .
  24. ^ Carter, Shan; Cox, Amanda (14 de febrero de 2011). "Propuesta presupuestaria de Obama para 2012: cómo se gastan 3,7 billones de dólares". The New York Times . Consultado el 15 de febrero de 2011 .
  25. ^ "Arte de mapas de árboles". Archivado desde el original el 5 de diciembre de 2023.
  26. ^ "Cada AlgoRiThm tiene ARTE en él: Proyecto de Arte en Mapas de Árboles". CPNAS . Archivado desde el original el 8 de octubre de 2023.
Wikimedia Commons tiene medios relacionados con Treemaps .
  • El Proyecto de Arte Treemap produjo una exhibición para las Academias Nacionales en Washington, DC
  • "Descubrimiento de inteligencia empresarial mediante visualizaciones de mapas de árbol", Ben Shneiderman , 11 de abril de 2006
  • Estudio exhaustivo y bibliografía sobre técnicas de visualización de árboles
  • Vliegen, Roel; van Wijk, Jarke J.; van der Linden, Erik-Jan (septiembre–octubre de 2006). "Visualizing Business Data with Generalized Treemaps" (PDF) . IEEE Transactions on Visualization and Computer Graphics . 12 (5): 789–796. doi :10.1109/TVCG.2006.200. PMID  17080801. S2CID  18891326. Archivado desde el original (PDF) el 24 de julio de 2011.
  • Historia de los mapas de árboles por Ben Shneiderman.
  • Exploración hipermedia con mapas dinámicos interactivos Artículo de Zizi y Beaudouin-Lafon que presenta el algoritmo de diseño de mapa de árbol cuadriculado (denominado en su momento "diseño de mapa de árbol mejorado").
  • Descripción de la Universidad de Indiana
  • Mapa de árbol interactivo en vivo basado en ofertas con descuento de colaboración colectiva de Flytail Group
  • Ejemplo de mapa de árbol en inglés de The Hive Group
  • Varios ejemplos de mapas de árbol realizados con Macrofocus TreeMap
  • Visualizaciones mediante mapas de árboles dinámicos y software de mapas de árboles en línea de drasticdata
Obtenido de "https://es.wikipedia.org/w/index.php?title=Mapeo de árboles&oldid=1234907040"