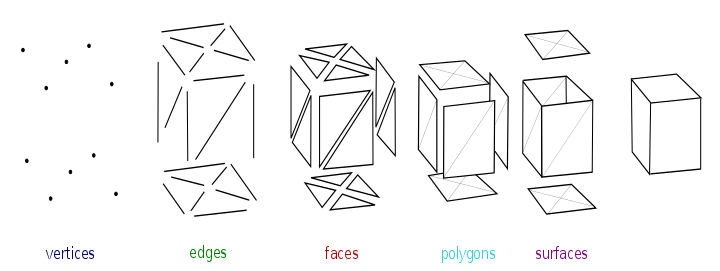
Malla poligonal
Este artículo necesita citas adicionales para su verificación . ( junio de 2009 ) |

En gráficos de computadora 3D y modelado de sólidos , una malla poligonal es una colección devértices ,borde sycara sque define la forma dela superficiede un objetopoliédrico. Simplificala representación, como en unmodelo de estructura alámbrica. Lascarassuelen constar detriángulos(malla de triángulos),cuadriláteros(cuadriláteros) u otrospolígonos convexos(n-gonos). Una malla poligonal también puede estar compuesta de forma más general porpolígonos cóncavoso inclusopolígonos con agujeros.
El estudio de las mallas poligonales es un gran subcampo de los gráficos por computadora (específicamente, los gráficos por computadora en 3D) y el modelado geométrico . Se utilizan diferentes representaciones de mallas poligonales para diferentes aplicaciones y objetivos. La variedad de operaciones realizadas en las mallas puede incluir: lógica booleana ( geometría sólida constructiva ), suavizado , simplificación y muchas otras. También existen algoritmos para el trazado de rayos , la detección de colisiones y la dinámica de cuerpos rígidos con mallas poligonales. Si se representan los bordes de la malla en lugar de las caras, entonces el modelo se convierte en un modelo de estructura alámbrica .
Existen varios métodos para la generación de mallas , incluido el algoritmo de cubos de marcha . [1]
Las mallas volumétricas se diferencian de las mallas poligonales en que representan explícitamente tanto la superficie como la región interior de una estructura, mientras que las mallas poligonales solo representan explícitamente la superficie (el volumen es implícito).
Elementos
Los objetos creados con mallas poligonales deben almacenar distintos tipos de elementos, como vértices, aristas, caras, polígonos y superficies. En muchas aplicaciones, solo se almacenan vértices, aristas y caras o polígonos. Un renderizador puede admitir solo caras de 3 lados, por lo que los polígonos deben construirse con muchas de ellas, como se muestra arriba. Sin embargo, muchos renderizadores admiten cuadriláteros y polígonos de más lados, o pueden convertir polígonos en triángulos sobre la marcha, lo que hace innecesario almacenar una malla en forma triangulada .
Representaciones
Las mallas poligonales se pueden representar de diversas maneras, utilizando distintos métodos para almacenar los datos de vértices, aristas y caras. Entre ellos se incluyen:
VVmalla " " representa únicamente vértices que apuntan a otros vértices. Tanto la información de las aristas como de las caras está implícita en la representación. Sin embargo, la simplicidad de la representación no permite realizar muchas operaciones eficientes en las mallas.Cada una de las representaciones anteriores tiene ventajas y desventajas particulares, que se analizan más a fondo en Smith (2006). [2] La elección de la estructura de datos está regida por la aplicación, el rendimiento requerido, el tamaño de los datos y las operaciones a realizar. Por ejemplo, es más fácil tratar con triángulos que con polígonos generales, especialmente en geometría computacional . Para ciertas operaciones es necesario tener un acceso rápido a información topológica como bordes o caras vecinas; esto requiere estructuras más complejas como la representación de borde alado. Para la representación de hardware, se necesitan estructuras compactas y simples; por lo tanto, la tabla de esquinas (abanico de triángulos) se incorpora comúnmente en las API de representación de bajo nivel como DirectX y OpenGL .
Mallas de vértice a vértice

Las mallas vértice-vértice representan un objeto como un conjunto de vértices conectados a otros vértices. Esta es la representación más simple, pero no se usa mucho porque la información de las caras y los bordes está implícita. Por lo tanto, es necesario recorrer los datos para generar una lista de caras para la representación. Además, las operaciones sobre los bordes y las caras no son fáciles de realizar.
Sin embargo, las mallas VV se benefician de un espacio de almacenamiento pequeño y una transformación eficiente de la forma. La figura anterior muestra una caja de cuatro lados representada por una malla VV. Cada vértice indexa sus vértices vecinos. Los dos últimos vértices, 8 y 9 en la parte superior e inferior central del "cilindro-caja", tienen cuatro vértices conectados en lugar de cinco. Un sistema general debe poder manejar una cantidad arbitraria de vértices conectados a cualquier vértice dado.
Para una descripción completa de las mallas VV, consulte Smith (2006). [2]
Mallas de caras y vértices

Las mallas de caras y vértices representan un objeto como un conjunto de caras y un conjunto de vértices. Esta es la representación de malla más utilizada y es la entrada que generalmente acepta el hardware gráfico moderno.
Las mallas de vértices de caras mejoran las mallas VV para el modelado, ya que permiten la búsqueda explícita de los vértices de una cara y las caras que rodean un vértice. La figura anterior muestra el ejemplo de "caja-cilindro" como una malla FV. El vértice v5 está resaltado para mostrar las caras que lo rodean. Observe que, en este ejemplo, se requiere que cada cara tenga exactamente 3 vértices. Sin embargo, esto no significa que cada vértice tenga la misma cantidad de caras circundantes.
Para la representación, la lista de caras se transmite generalmente a la GPU como un conjunto de índices para los vértices, y los vértices se envían como estructuras de posición/color/normal (en la figura, solo se proporciona la posición). Esto tiene la ventaja de que los cambios en la forma, pero no en la geometría, se pueden actualizar dinámicamente simplemente reenviando los datos de los vértices sin actualizar la conectividad de las caras.
El modelado requiere un recorrido sencillo de todas las estructuras. Con las mallas de caras y vértices es fácil encontrar los vértices de una cara. Además, la lista de vértices contiene una lista de caras conectadas a cada vértice. A diferencia de las mallas VV, tanto las caras como los vértices son explícitos, por lo que la localización de caras y vértices vecinos es un proceso de tiempo constante. Sin embargo, los bordes son implícitos, por lo que aún se necesita una búsqueda para encontrar todas las caras que rodean una cara determinada. Otras operaciones dinámicas, como dividir o fusionar una cara, también son difíciles con las mallas de caras y vértices.
Mallas con bordes alados
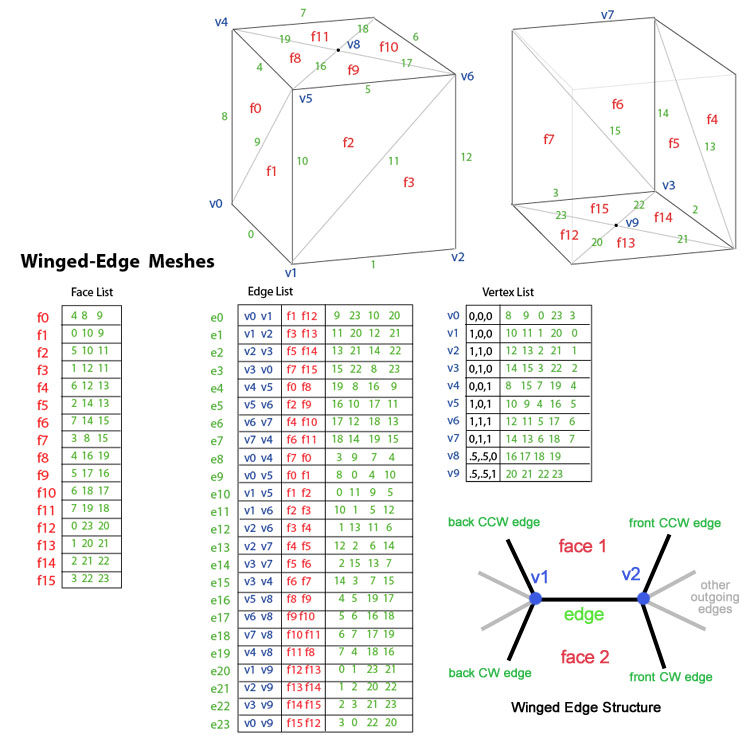
Introducidas por Baumgart en 1975, las mallas de aristas aladas representan explícitamente los vértices, las caras y las aristas de una malla. Esta representación se utiliza ampliamente en programas de modelado para proporcionar la mayor flexibilidad a la hora de cambiar dinámicamente la geometría de la malla, ya que las operaciones de división y fusión se pueden realizar rápidamente. Su principal inconveniente son los grandes requisitos de almacenamiento y la mayor complejidad debido al mantenimiento de muchos índices. Se puede encontrar un buen análisis de los problemas de implementación de las mallas de aristas aladas en el libro Graphics Gems II .
Las mallas de aristas con alas resuelven el problema de atravesar de arista a arista y proporcionar un conjunto ordenado de caras alrededor de una arista. Para cualquier arista dada, la cantidad de aristas salientes puede ser arbitraria. Para simplificar esto, las mallas de aristas con alas proporcionan solo cuatro, las aristas más cercanas en sentido horario y antihorario en cada extremo. Las otras aristas se pueden atravesar de manera incremental. Por lo tanto, la información para cada arista se asemeja a una mariposa, de ahí las mallas de "aristas con alas". La figura anterior muestra la "caja-cilindro" como una malla de aristas con alas. Los datos totales para una arista consisten en 2 vértices (puntos finales), 2 caras (en cada lado) y 4 aristas (arista con alas).
La representación de mallas de bordes con alas para hardware gráfico requiere la generación de una lista de índices de caras. Esto se hace generalmente solo cuando cambia la geometría. Las mallas de bordes con alas son ideales para geometría dinámica, como superficies de subdivisión y modelado interactivo, ya que los cambios en la malla pueden ocurrir localmente. El recorrido a través de la malla, como podría ser necesario para la detección de colisiones, se puede realizar de manera eficiente.
Véase Baumgart (1975) para más detalles. [3]
Renderizar mallas dinámicas
Las mallas de aristas con alas no son la única representación que permite cambios dinámicos en la geometría. Una nueva representación que combina mallas de aristas con alas y mallas de vértices de caras es la malla dinámica de renderizado , que almacena explícitamente tanto los vértices de una cara y las caras de un vértice (como las mallas FV) como las caras y los vértices de una arista (como las mallas de aristas con alas).
Las mallas dinámicas de renderizado requieren un poco menos de espacio de almacenamiento que las mallas de aristas con alas estándar y pueden renderizarse directamente mediante hardware gráfico, ya que la lista de caras contiene un índice de vértices. Además, el recorrido de vértice a cara es explícito (tiempo constante), al igual que de cara a vértice. Las mallas RD no requieren las cuatro aristas salientes, ya que se pueden encontrar recorriendo desde la arista hasta la cara y luego desde la cara hasta la arista vecina.
Las mallas RD se benefician de las características de las mallas de bordes alados al permitir que la geometría se actualice dinámicamente.
Véase Tobler y Maierhofer (WSCG 2006) para más detalles. [4]
Resumen de la representación de malla
| Operación | Vértice-vértice | Vértice de la cara | De borde alado | Renderizar dinámicamente | |
|---|---|---|---|---|---|
| VV | Todos los vértices alrededor del vértice | Explícito | V → f1, f2, f3, ... → v1, v2, v3, ... | V → e1, e2, e3, ... → v1, v2, v3, ... | V → e1, e2, e3, ... → v1, v2, v3, ... |
| ES | Todos los bordes de una cara | F(a,b,c) → {a,b}, {b,c}, {a,c} | F → {a,b}, {b,c}, {a,c} | Explícito | Explícito |
| VF | Todos los vértices de una cara | F(a,b,c) → {a,b,c} | Explícito | F → e1, e2, e3 → a, b, c | Explícito |
| VF | Todas las caras alrededor de un vértice | Búsqueda de pares | Explícito | V → e1, e2, e3 → f1, f2, f3, ... | Explícito |
| Vehículo eléctrico | Todas las aristas alrededor de un vértice | V → {v,v1}, {v,v2}, {v,v3}, ... | V → f1, f2, f3, ... → v1, v2, v3, ... | Explícito | Explícito |
| En fe | Ambas caras de un borde | Comparar listas | Comparar listas | Explícito | Explícito |
| VOY | Ambos vértices de una arista | E(a,b) → {a,b} | E(a,b) → {a,b} | Explícito | Explícito |
| Flujo | Encontrar la cara con los vértices dados | F(a,b,c) → {a,b,c} | Establecer intersección de v1,v2,v3 | Establecer intersección de v1,v2,v3 | Establecer intersección de v1,v2,v3 |
| Tamaño de almacenamiento | V*promedio(V,V) | 3F + V*promedio(F,V) | 3F + 8E + V*promedio(E,V) | 6F + 4E + V*promedio(E,V) | |
| Ejemplo con 10 vértices, 16 caras, 24 aristas: | |||||
| 10 * 5 = 50 | 3*16 + 10*5 = 98 | 3*16 + 8*24 + 10*5 = 290 | 6*16 + 4*24 + 10*5 = 242 | ||
| Figura 6: resumen de las operaciones de representación de malla | |||||
En la tabla anterior, explicit indica que la operación se puede realizar en tiempo constante, ya que los datos se almacenan directamente; list compare indica que se debe realizar una comparación de listas entre dos listas para realizar la operación; y pair search indica que se debe realizar una búsqueda en dos índices. La notación avg(V,V) significa el número promedio de vértices conectados a un vértice dado; avg(E,V) significa el número promedio de aristas conectadas a un vértice dado, y avg(F,V) es el número promedio de caras conectadas a un vértice dado.
La notación "V → f1, f2, f3, ... → v1, v2, v3, ..." describe que se requiere un recorrido a través de múltiples elementos para realizar la operación. Por ejemplo, para obtener "todos los vértices alrededor de un vértice dado V" utilizando la malla de cara-vértice, es necesario encontrar primero las caras alrededor del vértice dado V utilizando la lista de vértices. Luego, a partir de esas caras, utilizar la lista de caras para encontrar los vértices a su alrededor. Las mallas de aristas con alas almacenan explícitamente casi toda la información, y otras operaciones siempre recorren primero la arista para obtener información adicional. Las mallas de vértice-vértice son la única representación que almacena explícitamente los vértices vecinos de un vértice dado.
A medida que las representaciones de la malla se vuelven más complejas (de izquierda a derecha en el resumen), aumenta la cantidad de información almacenada explícitamente. Esto brinda un acceso más directo y constante en el tiempo al recorrido y la topología de varios elementos, pero a costa de un mayor gasto de espacio y de recursos para mantener los índices de manera adecuada.
La figura 7 muestra la información de conectividad para cada una de las cuatro técnicas descritas en este artículo. También existen otras representaciones, como las tablas de medio borde y de esquina. Todas ellas son variantes de cómo los vértices, las caras y los bordes se indexan entre sí.
Como regla general, las mallas de vértice-cara se utilizan siempre que se debe renderizar un objeto en hardware gráfico que no cambia la geometría (conectividad), pero puede deformar o transformar la forma (posiciones de vértice), como en el renderizado en tiempo real de objetos estáticos o que se transforman. Las mallas de borde alado o de renderizado dinámico se utilizan cuando cambia la geometría, como en paquetes de modelado interactivo o para calcular superficies de subdivisión. Las mallas de vértice-vértice son ideales para cambios complejos y eficientes en la geometría o la topología, siempre que el renderizado de hardware no sea un problema.
Otras representaciones
Formatos de archivos
Existen muchos formatos de archivo diferentes para almacenar datos de mallas poligonales. Cada formato es más eficaz cuando se utiliza para el propósito previsto por su creador. Los formatos más populares incluyen .fbx , .dae , .obj y .stl . A continuación, se presenta una tabla con algunos de estos formatos:
| Sufijo de archivo | Nombre del formato | Organización(es) | Programa(s) | Descripción |
|---|---|---|---|---|
| .crudo | Malla cruda | Desconocido | Varios | Formato abierto, solo ASCII. Cada línea contiene 3 vértices, separados por espacios, para formar un triángulo, como se muestra a continuación: X1 Y1 Z1 X2 Y2 Z2 X3 Y3 Z3 |
| .mezcla | Formato de archivo Blender | Fundación Blender | Licuadora 3D | Código abierto, formato únicamente binario |
| .fbx | Formato FBX de Autodesk | Autodesk | Varios | Propietario. Existen especificaciones binarias y ASCII. |
| .3ds | Archivo 3ds Max | Autodesk | 3ds máx. | Un formato común pero obsoleto con límites estrictos de 16 bits en la cantidad de vértices y caras. No está estandarizado ni bien documentado, pero solía ser un "estándar de facto" para el intercambio de datos. |
| .dae | Intercambio de activos digitales (COLLADA) | Sony Computer Entertainment , Grupo Khronos | N / A | Significa " Actividad de diseño colaborativo " . Un formato universal diseñado para evitar incompatibilidades. |
| .dgn | Archivo de MicroStation | Sistemas Bentley | Microestación | Hay dos formatos de archivo dgn: anterior a la versión 8 y versión 8 (V8) |
| .3dm | Archivo de Rhino | Robert McNeel & Asociados | Rinoceronte 3D | |
| .dxf , .dwg | Formato de intercambio de dibujos | Autodesk | AutoCAD | |
| .obj | OBJ de frente de onda | Tecnologías Wavefront | Varios | Formato ASCII que describe la geometría 3D. Los vértices de todas las caras están ordenados en sentido antihorario, lo que hace que las normales de las facetas sean implícitas. Las normales suaves se especifican por vértice. |
| .capa | Formato de archivo poligonal | Universidad de Stanford | Varios | Binario y ASCII |
| .pmd | Datos de Polygon Movie Maker | Yu Higuchi | MikuMikuBaile | Formato de archivo binario propietario para almacenar la geometría del modelo humanoide con información sobre aparejo, material y física. |
| .stl | Formato de estereolitografía | Sistemas 3D | Muchos | Formato binario y ASCII diseñado originalmente para ayudar en CNC . |
| .amf | Formato de archivo de fabricación aditiva | ASTM Internacional | N / A | Similar al formato STL, pero con soporte adicional para colores nativos, materiales y constelaciones. |
| .wrl | Lenguaje de modelado de realidad virtual | Consorcio Web3D | Navegadores web | Norma ISO 14772-1:1997 |
| .wrz | VRML comprimido | Consorcio Web3D | Navegadores web | |
| .x3d, .x3db, .x3dv | 3D extensible | Consorcio Web3D | Navegadores web | Basado en XML, de código abierto, libre de regalías, extensible e interoperable; también admite información sobre color, textura y escena. Norma ISO 19775/19776/19777 |
| .x3dz, .x3dbz, .x3dvz | Binario comprimido X3D | Consorcio Web3D | Navegadores web | |
| .c4d | Archivo Cinema 4D | Máximo | CINE 4D | |
| .dos | Archivo de objeto 3D de LightWave | Nueva Tek | Onda de luz 3D | |
| .pequeño | Puntuación de la APF | Puntuación RPI | PUMI | Mallas 3D no estructuradas adaptativas paralelas de código abierto para flujos de trabajo de simulación basados en PDE. |
| .msh | Malla Gmsh | Desarrolladores de GMsh | Proyecto GMsh | Código abierto, que proporciona una descripción de malla ASCII para elementos interpolados lineales y polinomiales en 1 a 3 dimensiones. |
| .malla | XML de OGRE | Equipo de desarrollo de OGRE | OGRE, básico puro | Código abierto. Formato binario (.mesh) y ASCII (.mesh.xml) disponibles. Incluye datos para animación de vértices y animación de destino de transformación (blendshape). Datos de animación esquelética en archivo independiente (.skeleton). |
| .vegetal | Malla tetraédrica FEM de Vega | Jernej Barbič | Vega FEM | Código abierto. Almacena una malla tetraédrica y sus propiedades materiales para simulación FEM. Formatos ASCII (.veg) y binario (.vegb) disponibles. |
| .z3d | Z3D | Oleg Melashenko | Modelador Zanoza | - |
| .vtk | Malla VTK | VTK , menaje | VTK , Paravista | Formato abierto, ASCII o binario que contiene muchos campos de datos diferentes, incluidos datos de puntos, datos de celdas y datos de campo. |
| .l4d | Dibujo LAI4D | Laboratorio de Inteligencia Artificial para el Diseño | LAI4D | Formato de datos ASCII que describe un árbol jerárquico de entidades. |
Véase también
- Representación de límites
- Operador de Euler
- Hipergrafo
- Variedad (una malla puede ser variedad o no variedad)
- Subdivisión de malla (una técnica para agregar detalles a una malla poligonal)
- Modelado de polígonos
- Poligonizador
- Simplex
- Spline en T
- Triangulación (geometría)
- Modelo de estructura alámbrica
Referencias
- ^ Lorensen, William E.; Cline, Harvey E. (1 de agosto de 1987). "Cubos de marcha: un algoritmo de construcción de superficies 3D de alta resolución". ACM SIGGRAPH Computer Graphics . 21 (4): 163–169. CiteSeerX 10.1.1.545.613 . doi :10.1145/37402.37422.
- ^ ab Colin Smith, Sobre las mallas vértice-vértice y su uso en el modelado geométrico y biológico, ( PDF )
- ^ Bruce Baumgart, Representación de poliedros con aristas aladas para visión artificial. Conferencia Nacional de Computación, mayo de 1975. "Uso de poliedros en visión artificial". baumgart.org . Mayo de 1975. Archivado desde el original el 29 de agosto de 2005. Consultado el 29 de agosto de 2005 .
- ^ Tobler & Maierhofer, Una estructura de datos en malla para renderización y subdivisión. 2006. ( PDF )
Enlaces externos
- Weisstein, Eric W. "Complejo simplicial". MathWorld .
- Weisstein, Eric W. "Triangulación". MathWorld .
- Representación de malla de medio borde de código abierto OpenMesh.
- Biblioteca de procesamiento de mallas poligonales