Módulo de corte

En la ciencia de los materiales , el módulo de corte o módulo de rigidez , denotado por G , o a veces S o μ , es una medida de la rigidez elástica al corte de un material y se define como la relación entre la tensión de corte y la deformación de corte : ^[1]

${\displaystyle G\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\tau _{xy}}{\gamma _{xy}}}={\frac {F/A}{ \Delta x/l}}={\frac {Fl}{A\Delta x}}}$

dónde

${\displaystyle \tau_{xy}=F/A\,}$= esfuerzo cortante

${\estilo de visualización F}$es la fuerza que actúa

${\estilo de visualización A}$es el área sobre la cual actúa la fuerza

$Estilo de visualización: gamma__{xy}$= deformación cortante. En ingeniería , en otros lugares${\displaystyle :=\Delta x/l=\tan \theta }$${\estilo de visualización :=\theta }$

${\displaystyle \Delta x}$es el desplazamiento transversal

${\estilo de visualización l}$es la longitud inicial del área.

La unidad derivada del SI del módulo de corte es el pascal (Pa), aunque normalmente se expresa en gigapascales (GPa) o en miles de libras por pulgada cuadrada (ksi). Su forma dimensional es M ¹ L ⁻¹ T ⁻² , reemplazando la fuerza por masa por aceleración .

El módulo de corte es una de las diversas magnitudes que se utilizan para medir la rigidez de los materiales. Todas ellas surgen de la ley generalizada de Hooke :

• El módulo de Young E describe la respuesta de deformación del material a la tensión uniaxial en la dirección de esta tensión (como tirar de los extremos de un cable o poner un peso sobre una columna, con el cable alargándose y la columna perdiendo altura).
• El coeficiente de Poisson ν describe la respuesta en las direcciones ortogonales a esta tensión uniaxial (el cable se vuelve más delgado y la columna más gruesa),
• El módulo volumétrico K describe la respuesta del material a la presión hidrostática (uniforme) (como la presión en el fondo del océano o en una piscina profunda),
• El módulo de corte G describe la respuesta del material al esfuerzo cortante (como cortarlo con tijeras sin filo).

Estos módulos no son independientes y, para los materiales isótropos, están conectados a través de las ecuaciones ^[9].

${\displaystyle E=2G(1+\nu )=3K(1-2\nu )}$

El módulo de corte se ocupa de la deformación de un sólido cuando experimenta una fuerza paralela a una de sus superficies mientras que su cara opuesta experimenta una fuerza opuesta (como la fricción). En el caso de un objeto con forma de prisma rectangular, se deformará hasta convertirse en un paralelepípedo . Los materiales anisotrópicos como la madera , el papel y también esencialmente todos los monocristales muestran una respuesta material diferente a la tensión o la deformación cuando se prueban en diferentes direcciones. En este caso, es posible que sea necesario utilizar la expresión tensorial completa de las constantes elásticas, en lugar de un único valor escalar.

Una posible definición de un fluido sería un material con módulo de corte cero.

En sólidos homogéneos e isótropos , existen dos tipos de ondas, ondas de presión y ondas de corte . La velocidad de una onda de corte está controlada por el módulo de corte. ${\displaystyle (v_{s})}$

${\displaystyle v_{s}={\sqrt {\frac {G}{\rho }}}}$

dónde

G es el módulo de corte

${\estilo de visualización \rho}$es la densidad del sólido .

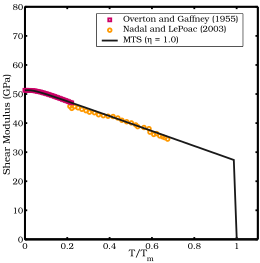
Se observa que el módulo de corte de los metales suele disminuir con el aumento de la temperatura. A presiones elevadas, el módulo de corte también parece aumentar con la presión aplicada. Se han observado correlaciones entre la temperatura de fusión, la energía de formación de vacantes y el módulo de corte en muchos metales. ^[13]

Existen varios modelos que intentan predecir el módulo de corte de los metales (y posiblemente el de las aleaciones). Los modelos de módulo de corte que se han utilizado en los cálculos de flujo plástico incluyen:

1. el modelo Varshni-Chen-Gray desarrollado por ^[14] y utilizado junto con el modelo de tensión de flujo plástico de esfuerzo umbral mecánico (MTS). ^{[15] [16]}
2. el modelo de módulo de corte de Steinberg-Cochran-Guinan (SCG) desarrollado por ^[17] y utilizado junto con el modelo de tensión de flujo de Steinberg-Cochran-Guinan-Lund (SCGL).
3. el modelo de módulo de corte de Nadal y LePoac (NP) ^[12] que utiliza la teoría de Lindemann para determinar la dependencia de la temperatura y el modelo SCG para la dependencia de la presión del módulo de corte.

El modelo de Varshni-Chen-Gray (a veces denominado ecuación de Varshni) tiene la forma:

${\displaystyle \mu(T)=\mu _{0}-{\frac {D}{\exp(T_{0}/T)-1}}}$

donde es el módulo de corte en , y y son constantes del material.${\displaystyle \mu_{0}}$${\estilo de visualización T=0K}$${\estilo de visualización D}$$Estilo de visualización T_{0}$

El modelo de módulo de corte de Steinberg-Cochran-Guinan (SCG) depende de la presión y tiene la forma

${\displaystyle \mu (p,T)=\mu _{0}+{\frac {\partial \mu }{\partial p}}{\frac {p}{\eta ^{\frac {1}{3}}}}+{\frac {\partial \mu }{\partial T}}(T-300);\quad \eta :={\frac {\rho }{\rho _{0}}}}$

donde, μ ₀ es el módulo de corte en el estado de referencia ( T = 300 K, p = 0, η = 1), p es la presión y T es la temperatura.

El modelo de módulo de corte de Nadal-Le Poac (NP) es una versión modificada del modelo SCG. La dependencia empírica de la temperatura del módulo de corte en el modelo SCG se reemplaza con una ecuación basada en la teoría de fusión de Lindemann . El modelo de módulo de corte NP tiene la forma:

${\displaystyle \mu (p,T)={\frac {1}{{\mathcal {J}}\left({\hat {T}}\right)}}\left[\left(\mu _{0}+{\frac {\partial \mu }{\partial p}}{\frac {p}{\eta ^{\frac {1}{3}}}}\right)\left(1-{\hat {T}}\right)+{\frac {\rho }{Cm}}~T\right];\quad C:={\frac {\left(6\pi ^{2}\right)^{\frac {2}{3}}}{3}}f^{2}}$

dónde

${\displaystyle {\mathcal {J}}({\hat {T}}):=1+\exp \left[-{\frac {1+1/\zeta }{1+\zeta /\left(1-{\hat {T}}\right)}}\right]\quad {\text{para}}\quad {\hat {T}}:={\frac {T}{T_{m}}}\in [0,6+\zeta ],}$

y μ ₀ es el módulo de corte en cero absoluto y presión ambiental, ζ es un área, m es la masa atómica y f es la constante de Lindemann .

El módulo de relajación de corte es la generalización dependiente del tiempo del módulo de corte ^[18] :$Estilo de visualización G(t)$ ${\estilo de visualización G}$

${\displaystyle G=\lim _{t\to \infty }G(t)}$.

• Tensor de elasticidad
• Módulo dinámico
• Técnica de excitación por impulsos
• Resistencia al corte
• Momento sísmico

Fórmulas de conversión
Los materiales elásticos lineales isótropos homogéneos tienen sus propiedades elásticas determinadas únicamente por cualesquiera dos módulos entre estos; por lo tanto, dados dos cualesquiera, cualquier otro de los módulos elásticos se puede calcular de acuerdo con estas fórmulas, siempre que se trate tanto de materiales 3D (primera parte de la tabla) como de materiales 2D (segunda parte).
Fórmulas 3D	${\displaystyle K=\,}$	${\estilo de visualización E=\,}$	${\displaystyle \lambda =\,}$	${\estilo de visualización G=\,}$	${\displaystyle \nu =\,}$	${\estilo de visualización M=\,}$	Notas
${\displaystyle (K,\,E)}$			${\displaystyle {\tfrac {3K(3K-E)}{9K-E}}}$	${\displaystyle {\tfrac {3KE}{9K-E}}}$	${\displaystyle {\tfrac {3K-E}{6K}}}$	${\displaystyle {\tfrac {3K(3K+E)}{9K-E}}}$
${\displaystyle (K,\,\lambda)}$		${\displaystyle {\tfrac {9K(K-\lambda )}{3K-\lambda }}}$		${\displaystyle {\tfrac {3(K-\lambda )}{2}}}$	${\displaystyle {\frac {\lambda }{3K-\lambda }}}$	${\estilo de visualización 3K-2\lambda \,}$
${\displaystyle (K,\,G)}$		${\displaystyle {\tfrac {9KG}{3K+G}}}$	${\displaystyle K-{\tfrac {2G}{3}}}$		${\displaystyle {\frac {3K-2G}{2(3K+G)}}}$	${\displaystyle K+{\tfrac {4G}{3}}}$
${\displaystyle (K,\,\nu )}$		${\displaystyle 3K(1-2\nu )\,}$	${\displaystyle {\tfrac {3K\nu }{1+\nu }}}$	${\displaystyle {\tfrac {3K(1-2\nu )}{2(1+\nu )}}}$		${\displaystyle {\tfrac {3K(1-\nu )}{1+\nu }}}$
${\displaystyle (K,\,M)}$		${\displaystyle {\tfrac {9K(MK)}{3K+M}}}$	${\displaystyle {\tfrac {3K-M}{2}}}$	${\displaystyle {\tfrac {3(M-K)}{4}}}$	${\displaystyle {\tfrac {3K-M}{3K+M}}}$
${\displaystyle (E,\,\lambda )}$	${\displaystyle {\tfrac {E+3\lambda +R}{6}}}$			${\displaystyle {\tfrac {E-3\lambda +R}{4}}}$	${\displaystyle {\tfrac {2\lambda }{E+\lambda +R}}}$	${\displaystyle {\tfrac {E-\lambda +R}{2}}}$	${\displaystyle R={\sqrt {E^{2}+9\lambda ^{2}+2E\lambda }}}$
${\displaystyle (E,\,G)}$	${\displaystyle {\tfrac {EG}{3(3G-E)}}}$		${\displaystyle {\tfrac {G(E-2G)}{3G-E}}}$		${\displaystyle {\tfrac {E}{2G}}-1}$	${\displaystyle {\tfrac {G(4G-E)}{3G-E}}}$
${\displaystyle (E,\,\nu )}$	${\displaystyle {\tfrac {E}{3(1-2\nu )}}}$		${\displaystyle {\tfrac {E\nu }{(1+\nu )(1-2\nu )}}}$	${\displaystyle {\tfrac {E}{2(1+\nu )}}}$		${\displaystyle {\tfrac {E(1-\nu )}{(1+\nu )(1-2\nu )}}}$
${\displaystyle (E,\,M)}$	${\displaystyle {\tfrac {3M-E+S}{6}}}$		${\displaystyle {\tfrac {M-E+S}{4}}}$	${\displaystyle {\tfrac {3M+E-S}{8}}}$	${\displaystyle {\tfrac {E-M+S}{4M}}}$		${\displaystyle S=\pm {\sqrt {E^{2}+9M^{2}-10EM}}}$ Hay dos soluciones válidas. El signo más lleva a .${\displaystyle \nu \geq 0}$ El signo menos lleva a .${\displaystyle \nu \leq 0}$
${\displaystyle (\lambda ,\,G)}$	${\displaystyle \lambda +{\tfrac {2G}{3}}}$	${\displaystyle {\tfrac {G(3\lambda +2G)}{\lambda +G}}}$			${\displaystyle {\tfrac {\lambda }{2(\lambda +G)}}}$	${\displaystyle \lambda +2G\,}$
${\displaystyle (\lambda ,\,\nu )}$	${\displaystyle {\tfrac {\lambda (1+\nu )}{3\nu }}}$	${\displaystyle {\tfrac {\lambda (1+\nu )(1-2\nu )}{\nu }}}$		${\displaystyle {\tfrac {\lambda (1-2\nu )}{2\nu }}}$		${\displaystyle {\tfrac {\lambda (1-\nu )}{\nu }}}$	No se puede utilizar cuando${\displaystyle \nu =0\Leftrightarrow \lambda =0}$
${\displaystyle (\lambda ,\,M)}$	${\displaystyle {\tfrac {M+2\lambda }{3}}}$	${\displaystyle {\tfrac {(M-\lambda )(M+2\lambda )}{M+\lambda }}}$		${\displaystyle {\tfrac {M-\lambda }{2}}}$	${\displaystyle {\tfrac {\lambda }{M+\lambda }}}$
${\displaystyle (G,\,\nu )}$	${\displaystyle {\tfrac {2G(1+\nu )}{3(1-2\nu )}}}$	${\displaystyle 2G(1+\nu )\,}$	${\displaystyle {\tfrac {2G\nu }{1-2\nu }}}$			${\displaystyle {\tfrac {2G(1-\nu )}{1-2\nu }}}$
${\displaystyle (G,\,M)}$	${\displaystyle M-{\tfrac {4G}{3}}}$	${\displaystyle {\tfrac {G(3M-4G)}{M-G}}}$	${\displaystyle M-2G\,}$		${\displaystyle {\tfrac {M-2G}{2M-2G}}}$
${\displaystyle (\nu ,\,M)}$	${\displaystyle {\tfrac {M(1+\nu )}{3(1-\nu )}}}$	${\displaystyle {\tfrac {M(1+\nu )(1-2\nu )}{1-\nu }}}$	${\displaystyle {\tfrac {M\nu }{1-\nu }}}$	${\displaystyle {\tfrac {M(1-2\nu )}{2(1-\nu )}}}$
Fórmulas 2D	${\displaystyle K_{\mathrm {2D} }=\,}$	${\displaystyle E_{\mathrm {2D} }=\,}$	${\displaystyle \lambda _{\mathrm {2D} }=\,}$	${\displaystyle G_{\mathrm {2D} }=\,}$	${\displaystyle \nu _{\mathrm {2D} }=\,}$	${\displaystyle M_{\mathrm {2D} }=\,}$	Notas
${\displaystyle (K_{\mathrm {2D} },\,E_{\mathrm {2D} })}$			${\displaystyle {\tfrac {2K_{\mathrm {2D} }(2K_{\mathrm {2D} }-E_{\mathrm {2D} })}{4K_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {K_{\mathrm {2D} }E_{\mathrm {2D} }}{4K_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {2K_{\mathrm {2D} }-E_{\mathrm {2D} }}{2K_{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {4K_{\mathrm {2D} }^{2}}{4K_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$
${\displaystyle (K_{\mathrm {2D} },\,\lambda _{\mathrm {2D} })}$		${\displaystyle {\tfrac {4K_{\mathrm {2D} }(K_{\mathrm {2D} }-\lambda _{\mathrm {2D} })}{2K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}}}$		${\displaystyle K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}$	${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }}{2K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}}}$	${\displaystyle 2K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}$
${\displaystyle (K_{\mathrm {2D} },\,G_{\mathrm {2D} })}$		${\displaystyle {\tfrac {4K_{\mathrm {2D} }G_{\mathrm {2D} }}{K_{\mathrm {2D} }+G_{\mathrm {2D} }}}}$	${\displaystyle K_{\mathrm {2D} }-G_{\mathrm {2D} }}$		${\displaystyle {\tfrac {K_{\mathrm {2D} }-G_{\mathrm {2D} }}{K_{\mathrm {2D} }+G_{\mathrm {2D} }}}}$	${\displaystyle K_{\mathrm {2D} }+G_{\mathrm {2D} }}$
${\displaystyle (K_{\mathrm {2D} },\,\nu _{\mathrm {2D} })}$		${\displaystyle 2K_{\mathrm {2D} }(1-\nu _{\mathrm {2D} })\,}$	${\displaystyle {\tfrac {2K_{\mathrm {2D} }\nu _{\mathrm {2D} }}{1+\nu _{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {K_{\mathrm {2D} }(1-\nu _{\mathrm {2D} })}{1+\nu _{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {2K_{\mathrm {2D} }}{1+\nu _{\mathrm {2D} }}}}$
${\displaystyle (E_{\mathrm {2D} },\,G_{\mathrm {2D} })}$	${\displaystyle {\tfrac {E_{\mathrm {2D} }G_{\mathrm {2D} }}{4G_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {2G_{\mathrm {2D} }(E_{\mathrm {2D} }-2G_{\mathrm {2D} })}{4G_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {E_{\mathrm {2D} }}{2G_{\mathrm {2D} }}}-1}$	${\displaystyle {\tfrac {4G_{\mathrm {2D} }^{2}}{4G_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$
${\displaystyle (E_{\mathrm {2D} },\,\nu _{\mathrm {2D} })}$	${\displaystyle {\tfrac {E_{\mathrm {2D} }}{2(1-\nu _{\mathrm {2D} })}}}$		${\displaystyle {\tfrac {E_{\mathrm {2D} }\nu _{\mathrm {2D} }}{(1+\nu _{\mathrm {2D} })(1-\nu _{\mathrm {2D} })}}}$	${\displaystyle {\tfrac {E_{\mathrm {2D} }}{2(1+\nu _{\mathrm {2D} })}}}$		${\displaystyle {\tfrac {E_{\mathrm {2D} }}{(1+\nu _{\mathrm {2D} })(1-\nu _{\mathrm {2D} })}}}$
${\displaystyle (\lambda _{\mathrm {2D} },\,G_{\mathrm {2D} })}$	${\displaystyle \lambda _{\mathrm {2D} }+G_{\mathrm {2D} }}$	${\displaystyle {\tfrac {4G_{\mathrm {2D} }(\lambda _{\mathrm {2D} }+G_{\mathrm {2D} })}{\lambda _{\mathrm {2D} }+2G_{\mathrm {2D} }}}}$			${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }}{\lambda _{\mathrm {2D} }+2G_{\mathrm {2D} }}}}$	${\displaystyle \lambda _{\mathrm {2D} }+2G_{\mathrm {2D} }\,}$
${\displaystyle (\lambda _{\mathrm {2D} },\,\nu _{\mathrm {2D} })}$	${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }(1+\nu _{\mathrm {2D} })}{2\nu _{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }(1+\nu _{\mathrm {2D} })(1-\nu _{\mathrm {2D} })}{\nu _{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }(1-\nu _{\mathrm {2D} })}{2\nu _{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }}{\nu _{\mathrm {2D} }}}}$	No se puede utilizar cuando${\displaystyle \nu _{\mathrm {2D} }=0\Leftrightarrow \lambda _{\mathrm {2D} }=0}$
${\displaystyle (G_{\mathrm {2D} },\,\nu _{\mathrm {2D} })}$	${\displaystyle {\tfrac {G_{\mathrm {2D} }(1+\nu _{\mathrm {2D} })}{1-\nu _{\mathrm {2D} }}}}$	${\displaystyle 2G_{\mathrm {2D} }(1+\nu _{\mathrm {2D} })\,}$	${\displaystyle {\tfrac {2G_{\mathrm {2D} }\nu _{\mathrm {2D} }}{1-\nu _{\mathrm {2D} }}}}$			${\displaystyle {\tfrac {2G_{\mathrm {2D} }}{1-\nu _{\mathrm {2D} }}}}$
${\displaystyle (G_{\mathrm {2D} },\,M_{\mathrm {2D} })}$	${\displaystyle M_{\mathrm {2D} }-G_{\mathrm {2D} }}$	${\displaystyle {\tfrac {4G_{\mathrm {2D} }(M_{\mathrm {2D} }-G_{\mathrm {2D} })}{M_{\mathrm {2D} }}}}$	${\displaystyle M_{\mathrm {2D} }-2G_{\mathrm {2D} }\,}$		${\displaystyle {\tfrac {M_{\mathrm {2D} }-2G_{\mathrm {2D} }}{M_{\mathrm {2D} }}}}$