Método matricial de líneas de transmisión

El método de la matriz de líneas de transmisión (TLM) es un método de discretización espacial y temporal para el cálculo de campos electromagnéticos . Se basa en la analogía entre el campo electromagnético y una malla de líneas de transmisión . El método TLM permite el cálculo de estructuras electromagnéticas tridimensionales complejas y ha demostrado ser uno de los métodos de dominio temporal más potentes junto con el método de dominio temporal de diferencias finitas ( FDTD ). El TLM fue explorado por primera vez por Raymond Beurle mientras trabajaba en English Electric Valve Company en Chelmsford . Después de haber sido nombrado profesor de ingeniería eléctrica en la Universidad de Nottingham en 1963, coescribió un artículo, "Solución numérica de problemas de dispersión bidimensional utilizando una matriz de líneas de transmisión", con Peter B. Johns en 1971. ^[1]

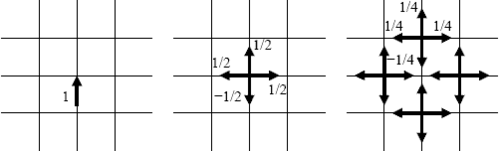
El método TLM se basa en el modelo de Huygens de propagación y dispersión de ondas y en la analogía entre propagación de campo y líneas de transmisión. Por lo tanto, considera el dominio computacional como una malla de líneas de transmisión, interconectadas en nodos. En la figura de la derecha se considera un ejemplo simple de una malla TLM 2D con un pulso de voltaje de amplitud 1 V incidente en el nodo central. Este pulso se reflejará parcialmente y se transmitirá de acuerdo con la teoría de líneas de transmisión. Si asumimos que cada línea tiene una impedancia característica , entonces el pulso incidente ve efectivamente tres líneas de transmisión en paralelo con una impedancia total de . El coeficiente de reflexión y el coeficiente de transmisión están dados por${\estilo de visualización Z}$${\estilo de visualización Z/3}$

${\displaystyle R={\frac {Z/3-Z}{Z/3+Z}}=-0,5}$

${\displaystyle T={\frac {2(Z/3)}{Z/3+Z}}=0,5}$

La energía inyectada en el nodo por el pulso incidente y la energía total de los pulsos dispersos son correspondientemente

${\displaystyle E_{I}=vi\,\Delta t=1\left(1/Z\right)\Delta t=\Delta t/Z}$

${\displaystyle E_{S}=\left[0,5^{2}+0,5^{2}+0,5^{2}+(-0,5)^{2}\right](\Delta t/Z)=\Delta t/Z}$

Por lo tanto, la ley de conservación de energía se cumple en el modelo.

El siguiente evento de dispersión excita los nodos vecinos según el principio descrito anteriormente. Se puede ver que cada nodo se convierte en una fuente secundaria de ondas esféricas. Estas ondas se combinan para formar la forma de onda general. Esto está de acuerdo con el principio de Huygens de propagación de la luz.

Para mostrar el esquema TLM utilizaremos discretización de tiempo y espacio. El paso de tiempo se denotará con y los intervalos de discretización de espacio con , y . Por lo tanto, el tiempo y el espacio absolutos serán , , , , donde es el instante de tiempo y son las coordenadas de la celda. En caso de que se utilice el valor , que es la constante de red . En este caso se cumple lo siguiente:${\displaystyle \Delta t}$${\displaystyle \Delta x}$${\displaystyle \Delta y}$${\displaystyle \Delta z}$${\displaystyle t=k\,\Delta t}$${\displaystyle x=l\,\Delta x}$${\displaystyle y=m\,\Delta y}$${\displaystyle z=n\,\Delta z}$${\displaystyle k=0,1,2,\lpuntos}$${\estilo de visualización m,n,l}$${\displaystyle \Delta x=\Delta y=\Delta z}$${\displaystyle \Delta l}$

${\displaystyle \Delta t={\frac {\Delta l}{c_{0}}},}$

¿Dónde está la velocidad de la luz en el espacio libre?$estilo de visualización c_{0}}$

Si consideramos una distribución de campo electromagnético en la que los únicos componentes distintos de cero son , y (es decir, una distribución en modo TE), entonces las ecuaciones de Maxwell en coordenadas cartesianas se reducen a$Estilo de visualización E_{x}}$${\displaystyle E_{y}}$$Estilo de visualización H_ {z}}$

${\displaystyle {\frac {\parcial {H_{z}}}{\parcial {y}}}=\varepsilon {\frac {\parcial {E_{x}}}{\parcial {t}}}}$

${\displaystyle -{\frac {\parcial {H_{z}}}{\parcial {x}}}=\varepsilon {\frac {\parcial {E_{y}}}{\parcial {t}}}}$

${\displaystyle {\frac {\parcial {E_{y}}}{\parcial {x}}}-{\frac {\parcial {E_{x}}}{\parcial {y}}}=-\mu {\frac {\parcial {H_{z}}}{\parcial {t}}}}$

Podemos combinar estas ecuaciones para obtener

${\displaystyle {\frac {\partial ^{2}H_{z}}{\partial {x}^{2}}}+{\frac {\partial ^{2}{H_{z}}}{\partial {y}^{2}}}=\mu \varepsilon {\frac {\partial ^{2}{H_{z}}}{\partial {t}^{2}}}}$

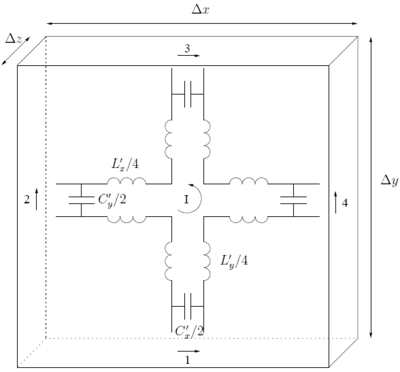
La figura de la derecha presenta una estructura denominada nodo en serie . Describe un bloque de dimensiones espaciales , y que consta de cuatro puertos. y son la inductancia y capacitancia distribuidas de las líneas de transmisión. Es posible demostrar que un nodo en serie es equivalente a una onda TE, más precisamente la corriente de malla I , los voltajes en la dirección x (puertos 1 y 3) y los voltajes en la dirección y (puertos 2 y 4) pueden estar relacionados con los componentes de campo , y . Si se consideran los voltajes en los puertos, , y se cumple la polaridad de la figura anterior, entonces lo siguiente es válido${\displaystyle \Delta x}$${\displaystyle \Delta y}$${\displaystyle \Delta z}$${\estilo de visualización L'}$${\estilo de visualización C'}$$Estilo de visualización H_ {z}}$$Estilo de visualización E_{x}}$${\displaystyle E_{y}}$$Estilo de visualización L_{x}=L_{y}}$

${\displaystyle -V_{1}+V_{2}+V_{3}-V_{4}=2L'\,\Delta l{\frac {\partial {I}}{\partial {t}}}}$

dónde .${\displaystyle \Delta x=\Delta y=\Delta l}$

${\displaystyle \left(V_{3}-V_{1}\right)-\left(V_{4}-V_{2}\right)=2L'\,\Delta l{\frac {\partial I}{\partial t}}}$

${\displaystyle \left[E_{x}(y+\Delta y)-E_{x}(y)\right]\,\Delta x-[E_{y}(x+\Delta x)-E_{y}(x)]\Delta y=2L'\,\Delta l{\frac {\partial {I}}{\partial {t}}}}$

y dividiendo ambos lados por${\displaystyle \Delta x\Delta y}$

${\displaystyle {\frac {E_{x}(y+\Delta y)-E_{x}(y)}{\Delta y}}-{\frac {E_{y}(x+\Delta x)-E_{y}(x)}{\Delta x}}=2L'\,\Delta l{\frac {\partial {I}}{\partial {t}}}{\frac {1}{\Delta x\,\Delta y}}}$

Dado que y sustituyendo se obtiene${\displaystyle \Delta x=\Delta y=\Delta z=\Delta l}$${\displaystyle I=H_{z}\,\Delta z}$

${\displaystyle {\frac {\Delta E_{x}}{\Delta y}}-{\frac {\Delta E_{y}}{\Delta x}}=2L'{\frac {\partial H_{z}}{\partial t}}}$

Esto se reduce a las ecuaciones de Maxwell cuando .${\displaystyle \Delta l\rightarrow 0}$

De manera similar, utilizando las condiciones en los capacitores de los puertos 1 y 4, se puede demostrar que las otras dos ecuaciones de Maxwell correspondientes son las siguientes:

${\displaystyle {\frac {\partial {H_{z}}}{\partial {y}}}=C'{\frac {\partial {E_{x}}}{\partial {t}}}}$

${\displaystyle -{\frac {\partial {H_{z}}}{\partial {x}}}=C'{\frac {\partial {E_{y}}}{\partial {t}}}}$

Con estos resultados, es posible calcular la matriz de dispersión de un nodo en derivación. El pulso de voltaje incidente en el puerto 1 en el paso de tiempo k se denota como . Reemplazando los cuatro segmentos de línea de la figura anterior con su equivalente de Thevenin, es posible demostrar que se cumple la siguiente ecuación para el pulso de voltaje reflejado:${\displaystyle _{k}V_{1}^{i}}$

${\displaystyle _{k}V_{1}^{r}=0.5\left(_{k}V_{1}^{i}+_{k}V_{2}^{i}+_{k}V_{3}^{i}-_{k}V_{4}^{i}\right)}$

Si todas las ondas incidentes así como todas las ondas reflejadas se recogen en un vector, entonces esta ecuación puede escribirse para todos los puertos en forma de matriz:

${\displaystyle _{k}\mathbf {V} ^{r}=\mathbf {S} _{k}\mathbf {V} ^{i}}$

donde y son los vectores de amplitud del pulso incidente y reflejado.${\displaystyle _{k}\mathbf {V} ^{i}}$${\displaystyle _{k}\mathbf {V} ^{r}}$

Para un nodo en serie la matriz de dispersión S tiene la siguiente forma

${\displaystyle \mathbf {S} ={\frac {1}{2}}\left[{\begin{array}{cccc}1&1&1&-1\\1&1&-1&1\\1&-1&1&1\\-1&1&1&1\end{array}}\right]}$

Para describir la conexión entre nodos adyacentes mediante una malla de nodos en serie, observe la figura de la derecha. Como el pulso incidente en el intervalo de tiempo k+1 sobre un nodo es el pulso disperso de un nodo adyacente en el intervalo de tiempo k , se derivan las siguientes ecuaciones de conexión:

${\displaystyle _{k+1}V_{1}^{i}(x,y)=_{k+1}V_{3}^{r}(x,y-1)}$

${\displaystyle _{k+1}V_{2}^{i}(x,y)=_{k+1}V_{4}^{r}(x-1,y)}$

${\displaystyle _{k+1}V_{3}^{i}(x,y)=_{k+1}V_{1}^{r}(x,y+1)}$

${\displaystyle _{k+1}V_{4}^{i}(x,y)=_{k+1}V_{2}^{r}(x+1,y)}$

Modificando la matriz de dispersión se pueden modelar materiales heterogéneos y con pérdidas. Ajustando las ecuaciones de conexión es posible simular diferentes límites.${\displaystyle {\textbf {S}}}$

Además del nodo en serie, descrito anteriormente, también existe el nodo TLM en derivación , que representa una distribución de campo en modo TM. Los únicos componentes distintos de cero de dicha onda son , , y . Con consideraciones similares a las del nodo en serie, se puede derivar la matriz de dispersión del nodo en derivación.${\displaystyle H_{x}}$${\displaystyle H_{y}}$${\displaystyle E_{z}}$

La mayoría de los problemas en electromagnetismo requieren una red tridimensional. Como ahora tenemos estructuras que describen distribuciones de campos TE y TM, intuitivamente parece posible definir una combinación de nodos en serie y en derivación que proporcionen una descripción completa del campo electromagnético. Se han hecho intentos de este tipo, pero debido a la complejidad de las estructuras resultantes, resultaron no ser muy útiles. El uso de la analogía que se presentó anteriormente conduce al cálculo de los diferentes componentes del campo en puntos separados físicamente. Esto causa dificultades para proporcionar definiciones de límites simples y eficientes. Johns proporcionó una solución a estos problemas en 1987, cuando propuso la estructura conocida como nodo condensado simétrico (SCN), que se presenta en la figura de la derecha. Consta de 12 puertos porque se deben asignar dos polarizaciones de campo a cada uno de los 6 lados de una celda de malla.

La topología del SCN no se puede analizar mediante circuitos equivalentes de Thevenin. Se deben utilizar principios más generales de conservación de energía y carga.

Los campos eléctricos y magnéticos en los lados del nodo número SCN (l,m,n) en el instante de tiempo k pueden resumirse en vectores de 12 dimensiones.

${\displaystyle _{k}\mathbf {E} _{l,m,n}=_{k}\left[E_{1},E_{2},\ldots ,E_{11},E_{12}\right]_{l,m,n}^{T}}$

${\displaystyle _{k}\mathbf {H} _{l,m,n}=_{k}\left[H_{1},H_{2},\ldots ,H_{11},H_{12}\right]_{l,m,n}^{T}}$

Se pueden vincular con los vectores de amplitud incidente y disperso mediante

${\displaystyle _{k}\mathbf {a} _{l,m,n}={\frac {1}{2{\sqrt {Z_{F}}}}}{_{k}\mathbf {E} }_{l,m,n}+{\frac {\sqrt {Z_{F}}}{2}}{_{k}\mathbf {H} }_{l,m,n}}$

${\displaystyle _{k}\mathbf {b} _{l,m,n}={\frac {1}{2{\sqrt {Z_{F}}}}}{_{k}\mathbf {E} }_{l,m,n}-{\frac {\sqrt {Z_{F}}}{2}}{_{k}\mathbf {H} }_{l,m,n}}$

donde es la impedancia de campo, es el vector de las amplitudes de las ondas incidentes en el nodo, y es el vector de las amplitudes dispersas. La relación entre las ondas incidentes y dispersas viene dada por la ecuación matricial${\displaystyle Z_{F}={\sqrt {\frac {\mu }{\varepsilon }}}}$${\displaystyle _{k}\mathbf {a} _{l,m,n}}$${\displaystyle _{k}\mathbf {b} _{l,m,n}}$

${\displaystyle _{k}\mathbf {b} _{l,m,n}=\mathbf {S} _{k}\mathbf {a} _{l,m,n}}$

Se puede calcular la matriz de dispersión S. Para el nodo condensado simétrico con puertos definidos como en la figura se obtiene el siguiente resultado

${\displaystyle \mathbf {S} =\left[{\begin{array}{ccc}0&\mathbf {S} _{0}&\mathbf {S} _{0}^{T}\\\mathbf {S} _{0}^{T}&0&\mathbf {S} _{0}\\\mathbf {S} _{0}&\mathbf {S} _{0}^{T}&0\end{array}}\right]}$

donde se utilizó la siguiente matriz

${\displaystyle \mathbf {S} _{0}={\frac {1}{2}}\left[{\begin{array}{cccc}0&0&1&-1\\0&0&-1&1\\1&1&0&0\\1&1&0&0\end{array}}\right]}$

La conexión entre diferentes SCN se realiza de la misma manera que para los nodos 2D.

El Instituto George Green para la Investigación Electromagnética (GGIEMR) ha publicado en código abierto una implementación eficiente de 3D-TLM, capaz de realizar cálculos paralelos por medio de MPI , denominada GGITLM y disponible en línea. ^[2]

• C. Christopoulos, El método de modelado de líneas de transmisión: TLM , Piscataway, NY, IEEE Press, 1995. ISBN 978-0-19-856533-8 
• Russer, P., Electromagnetismo, diseño de circuitos de microondas y antenas para ingeniería de comunicaciones, segunda edición, Artec House, Boston, 2006, ISBN 978-1-58053-907-4 
• PB Johns y MO'Brien. "Uso del método de modelado de líneas de transmisión (tlm) para resolver redes agrupadas no lineales", The Radio Electron and Engineer. 1980.
• JL Herring, Desarrollos en el método de modelado de líneas de transmisión para estudios de compatibilidad electromagnética, tesis doctoral, Universidad de Nottingham, 1993.
• Mansour Ahmadian, Tesis doctoral sobre modelado de ultrasonidos médicos mediante matriz de líneas de transmisión (TLM), Universidad de Edimburgo, 2001