Máquina de Moore

En la teoría de la computación , una máquina de Moore es una máquina de estados finitos cuyos valores de salida actuales están determinados únicamente por su estado actual . Esto contrasta con una máquina de Mealy , cuyos valores de salida están determinados tanto por su estado actual como por los valores de sus entradas. Al igual que otras máquinas de estados finitos, en las máquinas de Moore, la entrada normalmente influye en el siguiente estado. Por lo tanto, la entrada puede influir indirectamente en las salidas posteriores, pero no en la salida actual o inmediata. La máquina de Moore recibe su nombre de Edward F. Moore , quien presentó el concepto en un artículo de 1956, “ Gedanken-experiments on Sequential Machines”. ^[1]

Una máquina de Moore se puede definir como una tupla de 6 que consta de lo siguiente:${\displaystyle (S,s_{0},\Sigma ,O,\delta ,G)}$

• Un conjunto finito de estados ${\estilo de visualización S}$
• Un estado de inicio (también llamado estado inicial) que es un elemento de$estilo de visualización s_{0}$${\estilo de visualización S}$
• Un conjunto finito llamado alfabeto de entrada ${\estilo de visualización \Sigma}$
• Un conjunto finito llamado alfabeto de salida ${\estilo de visualización O}$
• Una función de transición que asigna un estado y el alfabeto de entrada al siguiente estado${\displaystyle \delta :S\times \Sigma \rightarrow S}$
• Una función de salida que asigna cada estado al alfabeto de salida${\displaystyle G:S\arrow derecha O}$

La "evolución a través del tiempo" se realiza en esta abstracción haciendo que la máquina de estados consulte el símbolo de entrada que cambia el tiempo en "tictacs del temporizador" discretos y reaccione de acuerdo con su configuración interna en esos instantes idealizados, o bien haciendo que la máquina de estados espere el siguiente símbolo de entrada (como en un FIFO) y reaccione cuando llega.$estilo de visualización t_{0},t_{1},t_{2},...}$

Una máquina de Moore puede considerarse un tipo restringido de transductor de estados finitos .

Una tabla de transición de estados es una tabla que enumera todos los triples en la relación de transición .${\displaystyle \delta :S\times \Sigma \rightarrow S}$

El diagrama de estados de una máquina de Moore, o diagrama de Moore, es un diagrama de estados que asocia un valor de salida con cada estado.

Como las máquinas de Moore y Mealy son ambos tipos de máquinas de estados finitos, son igualmente expresivas: cualquiera de los dos tipos puede usarse para analizar un lenguaje regular .

La diferencia entre las máquinas de Moore y las máquinas de Mealy es que en estas últimas, la salida de una transición está determinada por la combinación del estado actual y la entrada actual ( como el dominio de ), en lugar de solo el estado actual ( como el dominio de ). Cuando se representa como un diagrama de estados ,${\displaystyle S\times \Sigma}$${\estilo de visualización G}$${\estilo de visualización S}$${\estilo de visualización G}$

• Para una máquina Moore, cada nodo (estado) está etiquetado con un valor de salida;
• Para una máquina Mealy, cada arco (transición) está etiquetado con un valor de salida.

Cada máquina de Moore es equivalente a la máquina Mealy con los mismos estados y transiciones y la función de salida , que toma cada par estado-entrada y produce , donde es la función de salida de y es la función de transición de .${\estilo de visualización M}$${\displaystyle G(s,\sigma)=G_{M}(\delta _{M}(s,\sigma))}$${\estilo de visualización (s,\sigma)}$${\displaystyle G_{M}(\delta _{M}(s,\sigma ))}$$Estilo de visualización G_ {M}}$${\estilo de visualización M}$${\displaystyle \delta _{M}}$${\estilo de visualización M}$

Sin embargo, no todas las máquinas Mealy se pueden convertir en una máquina Moore equivalente. Algunas solo se pueden convertir en una máquina Moore casi equivalente, con salidas desplazadas en el tiempo. Esto se debe a la forma en que las etiquetas de estado se emparejan con las etiquetas de transición para formar los pares de entrada/salida. Considere una transición de estado a estado . La entrada que causa la transición etiqueta el borde . La salida correspondiente a esa entrada es la etiqueta de estado . ^[2] Observe que este es el estado de origen de la transición. Entonces, para cada entrada, la salida ya está fijada antes de que se reciba la entrada y depende únicamente del estado actual. Esta es la definición original de E. Moore. Es un error común usar la etiqueta de estado como salida para la transición .${\displaystyle s_{i}\rightarrow s_{j}}$$estilo de visualización s_{i}}$$estilo de visualización s_ {j}}$${\displaystyle s_{i}\rightarrow s_{j}}$${\displaystyle (s_{i},s_{j})}$$estilo de visualización s_{i}}$$estilo de visualización s_ {j}}$${\displaystyle s_{i}\rightarrow s_{j}}$

Tipos según número de entradas/salidas.

Las máquinas de Moore simples tienen una entrada y una salida:

• Detector de bordes mediante XOR
• máquina sumadora binaria
• sistemas secuenciales sincronizados (una forma restringida de la máquina de Moore donde el estado cambia solo cuando cambia la señal del reloj global)

La mayoría de los sistemas electrónicos digitales están diseñados como sistemas secuenciales sincronizados . Los sistemas secuenciales sincronizados son una forma restringida de la máquina de Moore donde el estado cambia solo cuando cambia la señal de reloj global. Normalmente, el estado actual se almacena en flip-flops y una señal de reloj global se conecta a la entrada de "reloj" de los flip-flops. Los sistemas secuenciales sincronizados son una forma de resolver problemas de metaestabilidad . Una máquina de Moore electrónica típica incluye una cadena lógica combinacional para decodificar el estado actual en las salidas (lambda). En el instante en que cambia el estado actual, esos cambios se propagan a través de esa cadena y casi instantáneamente la salida se actualiza. Existen técnicas de diseño para garantizar que no se produzcan fallos en las salidas durante ese breve período mientras esos cambios se propagan a través de la cadena, pero la mayoría de los sistemas están diseñados para que los fallos durante ese breve tiempo de transición se ignoren o sean irrelevantes. Las salidas permanecen iguales indefinidamente ( los LED permanecen brillantes, la energía permanece conectada a los motores, los solenoides permanecen energizados, etc.), hasta que la máquina de Moore cambia de estado nuevamente.

Una red secuencial tiene una entrada y una salida. La salida se convierte en 1 y permanece 1 a partir de entonces cuando se han producido al menos dos 0 y dos 1 como entradas.

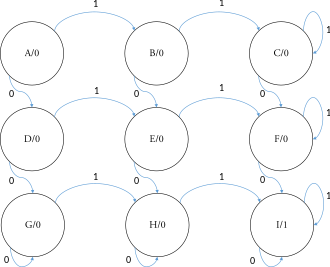
A la derecha se muestra una máquina de Moore con nueve estados para la descripción anterior. El estado inicial es el estado A y el estado final es el estado I. La tabla de estados para este ejemplo es la siguiente:

Las máquinas de Moore más complejas pueden tener múltiples entradas y múltiples salidas.

En el artículo de Moore de 1956 " Gedanken-experiments on Sequential Machines", ^[1] los autómatas (o máquinas) se definen como poseedores de estados, símbolos de entrada y símbolos de salida. Se demuestran nueve teoremas sobre la estructura de , y se realizan experimentos con . Más tarde, las " máquinas" pasaron a conocerse como "máquinas de Moore".${\estilo de visualización (n;m;p)}$${\estilo de visualización S}$${\estilo de visualización n}$${\estilo de visualización m}$${\estilo de visualización p}$${\estilo de visualización S}$${\estilo de visualización S}$${\estilo de visualización S}$

Al final del trabajo, en el apartado “Otros problemas”, se plantea la siguiente tarea:

Otro problema que se deriva directamente es la mejora de los límites dados en los teoremas 8 y 9.

El teorema 8 de Moore se formula como:

Dada una máquina arbitraria , tal que cada dos de sus estados son distinguibles entre sí, entonces existe un experimento de longitud que determina el estado de al final del experimento.${\estilo de visualización (n;m;p)}$${\estilo de visualización S}$${\displaystyle {\tfrac {n(n-1)}{2}}}$${\estilo de visualización S}$

En 1957, AA Karatsuba demostró los dos teoremas siguientes, que resolvieron completamente el problema de Moore sobre la mejora de los límites de la longitud del experimento de su "Teorema 8".

Teorema A. Si es una máquina tal que cada dos de sus estados son distinguibles entre sí, entonces existe un experimento ramificado de longitud como máximo mediante el cual se puede determinar el estado de al final del experimento.${\estilo de visualización S}$${\estilo de visualización (n;m;p)}$${\displaystyle {\tfrac {(n-1)(n-2)}{2}}+1}$${\estilo de visualización S}$

Teorema B. Existe una máquina, cuyos dos estados son distinguibles entre sí, tales que la duración de los experimentos más cortos que establecen el estado de la máquina al final del experimento es igual a .${\estilo de visualización (n;m;p)}$${\displaystyle {\tfrac {(n-1)(n-2)}{2}}+1}$

Los teoremas A y B sirvieron de base para el trabajo de curso del alumno de cuarto año A. A. Karatsuba, "Sobre un problema de la teoría de autómatas", que obtuvo una mención honorífica en el concurso de trabajos de estudiantes de la Facultad de Mecánica y Matemáticas de la Universidad Estatal de Moscú en 1958. El trabajo de Karatsuba fue entregado a la revista Uspekhi Mat. Nauk el 17 de diciembre de 1958 y publicado allí en junio de 1960. ^[3]

Hasta el día de hoy (2011), el resultado de Karatsuba sobre la duración de los experimentos es el único resultado no lineal exacto, tanto en la teoría de autómatas como en problemas similares de la teoría de la complejidad computacional .

• Circuito sincrónico
• Maquina harinosa
• Máquina de estados algorítmica
• Sistema autónomo (matemáticas)

• Conway, JH (1971). Álgebra regular y máquinas finitas . Londres: Chapman and Hall. ISBN 0-412-10620-5.Zbl 0231.94041  .
• Moore EF Experimentos experimentales sobre máquinas secuenciales. Automata Studies, Annals of Mathematical Studies, 34, 129–153. Princeton University Press, Princeton, NJ (1956).
• Karatsuba AA Solución de un problema a partir de la teoría de autómatas finitos. Usp. Mat. Nauk, 15:3, 157–159 (1960).
• Karatsuba AA Experimente mit Automaten (alemán) Elektron. Informaciónverarb. Kybernetik, 11, 611–612 (1975).
• Karatsuba AA Lista de trabajos de investigación .

La máquina de Moore y Mealy

• Medios relacionados con la máquina de Moore en Wikimedia Commons