Máquina de estados finitos
Una máquina de estados finitos ( FSM ) o autómata de estados finitos ( FSA , plural: autómatas ), autómata finito o simplemente máquina de estados , es un modelo matemático de computación . Es una máquina abstracta que puede estar en exactamente uno de un número finito de estados en un momento dado. La FSM puede cambiar de un estado a otro en respuesta a algunas entradas ; el cambio de un estado a otro se llama transición . [1] Una FSM se define por una lista de sus estados, su estado inicial y las entradas que activan cada transición. Las máquinas de estados finitos son de dos tipos: máquinas de estados finitos deterministas y máquinas de estados finitos no deterministas . [2] Para cualquier máquina de estados finitos no determinista, se puede construir una determinista equivalente.
El comportamiento de las máquinas de estados se puede observar en muchos dispositivos de la sociedad moderna que realizan una secuencia predeterminada de acciones en función de una secuencia de eventos que se les presentan. Ejemplos sencillos son: las máquinas expendedoras , que dispensan productos cuando se deposita la combinación adecuada de monedas; los ascensores , cuya secuencia de paradas está determinada por los pisos solicitados por los pasajeros; los semáforos , que cambian de secuencia cuando hay automóviles esperando; las cerraduras de combinación , que requieren la introducción de una secuencia de números en el orden adecuado.
La máquina de estados finitos tiene menos poder computacional que algunos otros modelos de computación como la máquina de Turing . [3] La distinción de poder computacional significa que hay tareas computacionales que una máquina de Turing puede hacer pero una FSM no. Esto se debe a que la memoria de una FSM está limitada por el número de estados que tiene. Una máquina de estados finitos tiene el mismo poder computacional que una máquina de Turing que está restringida de tal manera que su cabeza solo puede realizar operaciones de "lectura", y siempre tiene que moverse de izquierda a derecha. Las FSM se estudian en el campo más general de la teoría de autómatas .
Ejemplo: torniquete operado con monedas


Un ejemplo de un mecanismo simple que puede ser modelado por una máquina de estados es un torniquete . [4] [5] Un torniquete, utilizado para controlar el acceso al metro y a las atracciones de los parques de atracciones, es una puerta con tres brazos giratorios a la altura de la cintura, uno de ellos a lo ancho de la entrada. Inicialmente, los brazos están bloqueados, bloqueando la entrada, impidiendo el paso de los clientes. Al depositar una moneda o ficha en una ranura del torniquete, se desbloquean los brazos, lo que permite que un solo cliente pase. Después de que el cliente pasa, los brazos se bloquean nuevamente hasta que se inserta otra moneda.
Considerado como una máquina de estados, el torniquete tiene dos estados posibles: Locked y Unlocked . [4] Hay dos posibles entradas que afectan a su estado: poner una moneda en la ranura ( coin ) y empujar el brazo ( push ). En el estado bloqueado, empujar el brazo no tiene ningún efecto; no importa cuántas veces se dé la entrada push , permanece en el estado bloqueado. Poner una moneda, es decir, dar a la máquina una entrada de moneda , cambia el estado de Locked a Unlocked . En el estado desbloqueado, poner monedas adicionales no tiene ningún efecto; es decir, dar entradas de monedas adicionales no cambia el estado. Un cliente que empuja a través de los brazos da una entrada push y restablece el estado a Locked .
La máquina de estados del torniquete se puede representar mediante una tabla de transición de estados , que muestra para cada estado posible, las transiciones entre ellos (según las entradas proporcionadas a la máquina) y las salidas resultantes de cada entrada:
Estado actual Aporte Próximo estado Producción Bloqueado acuñar Desbloqueado Desbloquea el torniquete para que el cliente pueda pasar. empujar Bloqueado Ninguno Desbloqueado acuñar Desbloqueado Ninguno empujar Bloqueado Cuando el cliente ha pasado, se bloquea el torniquete.
La máquina de estados del torniquete también se puede representar mediante un gráfico dirigido llamado diagrama de estados (arriba) . Cada estado está representado por un nodo ( círculo ). Los bordes ( flechas ) muestran las transiciones de un estado a otro. Cada flecha está etiquetada con la entrada que activa esa transición. Una entrada que no causa un cambio de estado (como una entrada de moneda en el estado Desbloqueado ) está representada por una flecha circular que regresa al estado original. La flecha hacia el nodo Bloqueado desde el punto negro indica que es el estado inicial.
Conceptos y terminología
Un estado es una descripción del estado de un sistema que está esperando para ejecutar una transición . Una transición es un conjunto de acciones que se ejecutarán cuando se cumpla una condición o cuando se reciba un evento. Por ejemplo, cuando se utiliza un sistema de audio para escuchar la radio (el sistema está en el estado "radio"), recibir un estímulo "próximo" da como resultado pasar a la siguiente estación. Cuando el sistema está en el estado "CD", el estímulo "próximo" da como resultado pasar a la siguiente pista. Estímulos idénticos desencadenan diferentes acciones según el estado actual.
En algunas representaciones de máquinas de estados finitos, también es posible asociar acciones con un estado:
- una acción de entrada: se realiza al ingresar al estado, y
- una acción de salida: se realiza al salir del estado.
Representaciones

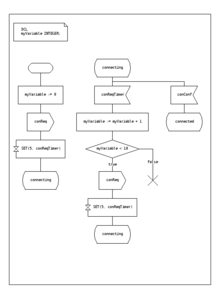
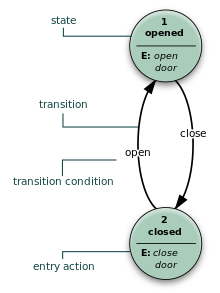
Tabla de estados/eventos
Se utilizan varios tipos de tablas de transición de estados . La representación más común se muestra a continuación: la combinación del estado actual (por ejemplo, B) y la entrada (por ejemplo, Y) muestra el siguiente estado (por ejemplo, C). La información completa de la acción no se describe directamente en la tabla y solo se puede agregar mediante notas al pie. [ Se necesita más explicación ] Es posible una definición de FSM que incluya la información completa de la acción mediante tablas de estados (consulte también la máquina virtual de estados finitos ).
Estado actual Aporte | Estado A | Estado B | Estado C |
|---|---|---|---|
| Entrada X | ... | ... | ... |
| Entrada Y | ... | Estado C | ... |
| Entrada Z | ... | ... | ... |
Máquinas de estados UML
El lenguaje de modelado unificado tiene una notación para describir las máquinas de estados. Las máquinas de estados UML superan las limitaciones [ cita requerida ] de las máquinas de estados finitos tradicionales al tiempo que conservan sus principales beneficios. Las máquinas de estados UML introducen los nuevos conceptos de estados anidados jerárquicamente y regiones ortogonales , al tiempo que extienden la noción de acciones . Las máquinas de estados UML tienen las características tanto de las máquinas Mealy como de las máquinas de Moore . Admiten acciones que dependen tanto del estado del sistema como del evento desencadenante , como en las máquinas Mealy , así como acciones de entrada y salida , que están asociadas con estados en lugar de transiciones, como en las máquinas de Moore. [ cita requerida ]
Máquinas de estados SDL
El lenguaje de especificación y descripción es un estándar de la UIT que incluye símbolos gráficos para describir acciones en la transición:
- enviar un evento
- recibir un evento
- iniciar un temporizador
- cancelar un temporizador
- Iniciar otra máquina de estados concurrentes
- decisión
SDL incorpora tipos de datos básicos llamados "Tipos de datos abstractos", un lenguaje de acción y una semántica de ejecución para hacer que la máquina de estados finitos sea ejecutable. [ cita requerida ]
Otros diagramas de estados
Existe una gran cantidad de variantes para representar un FSM como el de la figura 3.
Uso
Además de su uso en el modelado de sistemas reactivos presentados aquí, las máquinas de estados finitos son significativas en muchas áreas diferentes, incluyendo la ingeniería eléctrica , la lingüística , la informática , la filosofía , la biología , las matemáticas , la programación de videojuegos y la lógica . Las máquinas de estados finitos son una clase de autómatas estudiados en la teoría de autómatas y la teoría de la computación . En informática, las máquinas de estados finitos se utilizan ampliamente en el modelado del comportamiento de las aplicaciones ( teoría de control ), el diseño de sistemas digitales de hardware , la ingeniería de software , los compiladores , los protocolos de red y la lingüística computacional .
Clasificación
Las máquinas de estados finitos se pueden subdividir en aceptores, clasificadores, transductores y secuenciadores. [6]
Aceptantes


Los aceptadores (también llamados detectores o reconocedores ) producen una salida binaria, que indica si la entrada recibida es aceptada o no. Cada estado de un aceptador es de aceptación o de no aceptación . Una vez que se ha recibido toda la entrada, si el estado actual es de aceptación, la entrada es aceptada; de lo contrario, es rechazada. Como regla general, la entrada es una secuencia de símbolos (caracteres); no se utilizan acciones. El estado inicial también puede ser de aceptación, en cuyo caso el aceptador acepta la cadena vacía. El ejemplo de la figura 4 muestra un aceptador que acepta la cadena "nice". En este aceptador, el único estado de aceptación es el estado 7.
Un conjunto (posiblemente infinito) de secuencias de símbolos, llamado lenguaje formal , es un lenguaje regular si existe algún aceptor que acepte exactamente ese conjunto. Por ejemplo, el conjunto de cadenas binarias con un número par de ceros es un lenguaje regular (cf. Fig. 5), mientras que el conjunto de todas las cadenas cuya longitud es un número primo no lo es. [7] : 18, 71
También se podría decir que un aceptor define un lenguaje que contendría todas las cadenas aceptadas por el aceptor pero ninguna de las rechazadas; ese lenguaje es aceptado por el aceptor. Por definición, los lenguajes aceptados por los aceptores son los lenguajes regulares .
El problema de determinar el lenguaje aceptado por un aceptor dado es una instancia del problema de la ruta algebraica —en sí mismo una generalización del problema de la ruta más corta a gráficos con aristas ponderadas por los elementos de un semianillo (arbitrario) —. [8] [9] [ jerga ]
En la figura 5 aparece un ejemplo de un estado de aceptación: un autómata finito determinista (DFA) que detecta si la cadena de entrada binaria contiene un número par de 0.
S 1 (que también es el estado de inicio) indica el estado en el que se ha introducido un número par de 0. Por lo tanto, S 1 es un estado de aceptación. Este aceptador finalizará en un estado de aceptación si la cadena binaria contiene un número par de 0 (incluida cualquier cadena binaria que no contenga 0). Algunos ejemplos de cadenas aceptadas por este aceptador son ε (la cadena vacía ), 1, 11, 11..., 00, 010, 1010, 10110, etc.
Clasificadores
Los clasificadores son una generalización de los aceptores que producen una salida n -aria donde n es estrictamente mayor que dos. [10]
Transductores

Los transductores producen una salida en función de una entrada determinada y/o de un estado mediante acciones. Se utilizan para aplicaciones de control y en el campo de la lingüística computacional .
En aplicaciones de control se distinguen dos tipos:
- Máquina de Moore
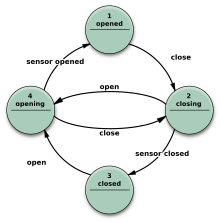
- El modelo de Moore utiliza únicamente acciones de entrada, es decir, la salida depende únicamente del estado. La ventaja del modelo de Moore es una simplificación del comportamiento. Consideremos la puerta de un ascensor. La máquina de estados reconoce dos comandos: "command_open" y "command_close", que activan cambios de estado. La acción de entrada (E:) en el estado "Opening" pone en marcha un motor que abre la puerta, la acción de entrada en el estado "Closing" pone en marcha un motor en la otra dirección que cierra la puerta. Los estados "Opened" y "Closed" detienen el motor cuando está completamente abierto o cerrado. Señalan al mundo exterior (por ejemplo, a otras máquinas de estados) la situación: "la puerta está abierta" o "la puerta está cerrada".
- Maquina harinosa
- La FSM también utiliza acciones de entrada, es decir, la salida depende de la entrada y el estado. El uso de una FSM Mealy conduce a menudo a una reducción del número de estados. El ejemplo de la figura 7 muestra una FSM Mealy que implementa el mismo comportamiento que en el ejemplo de Moore (el comportamiento depende del modelo de ejecución de FSM implementado y funcionará, por ejemplo, para FSM virtuales pero no para FSM controlados por eventos ). Hay dos acciones de entrada (I:): "iniciar el motor para cerrar la puerta si llega command_close" y "iniciar el motor en la otra dirección para abrir la puerta si llega command_open". Los estados intermedios "apertura" y "cierre" no se muestran.
Secuenciadores
Los secuenciadores (también llamados generadores ) son una subclase de aceptores y transductores que tienen un alfabeto de entrada de una sola letra. Producen una sola secuencia, que puede verse como una secuencia de salida de salidas del aceptor o del transductor. [6]
Determinismo
Otra distinción es entre autómatas deterministas ( DFA ) y no deterministas ( NFA , GNFA ). En un autómata determinista, cada estado tiene exactamente una transición para cada entrada posible. En un autómata no determinista, una entrada puede conducir a una, más de una o ninguna transición para un estado dado. El algoritmo de construcción de conjuntos de potencias puede transformar cualquier autómata no determinista en un autómata determinista (normalmente más complejo) con funcionalidad idéntica.
Una máquina de estados finitos con un solo estado se denomina "máquina de estados finitos combinatoria". Solo permite acciones en la transición a un estado. Este concepto es útil en casos en los que se requiere que varias máquinas de estados finitos trabajen juntas y cuando es conveniente considerar una parte puramente combinatoria como una forma de máquina de estados finitos para adaptarse a las herramientas de diseño. [11]
Semántica alternativa
Existen otros conjuntos de semánticas disponibles para representar máquinas de estados. Por ejemplo, existen herramientas para modelar y diseñar lógica para controladores embebidos. [12] Combinan máquinas de estados jerárquicas (que normalmente tienen más de un estado actual), gráficos de flujo y tablas de verdad en un solo lenguaje, lo que da como resultado un formalismo y un conjunto de semánticas diferentes. [13] Estos gráficos, al igual que las máquinas de estados originales de Harel , [14] admiten estados anidados jerárquicamente, regiones ortogonales , acciones de estado y acciones de transición. [15]
Modelo matemático
De acuerdo con la clasificación general, se encuentran las siguientes definiciones formales.
Una máquina de estados finitos determinista o un aceptor de estados finitos determinista es un quíntuple , donde:
- es el alfabeto de entrada (un conjunto finito no vacío de símbolos);
- es un conjunto finito no vacío de estados;
- es un estado inicial, un elemento de ;
- es la función de transición de estado: (en un autómata finito no determinista sería , es decir, devolvería un conjunto de estados);
- es el conjunto de estados finales, un subconjunto (posiblemente vacío) de .
Tanto para las FSM deterministas como para las no deterministas, es convencional permitir que sea una función parcial , es decir, no tiene que estar definida para cada combinación de y . Si una FSM está en un estado , el siguiente símbolo es y no está definido, entonces puede anunciar un error (es decir, rechazar la entrada). Esto es útil en las definiciones de máquinas de estados generales, pero menos útil cuando se transforma la máquina. Algunos algoritmos en su forma predeterminada pueden requerir funciones totales.
Una máquina de estados finitos tiene la misma capacidad computacional que una máquina de Turing que está restringida de tal manera que su cabeza sólo puede realizar operaciones de "lectura" y siempre tiene que moverse de izquierda a derecha. Es decir, cada lenguaje formal aceptado por una máquina de estados finitos es aceptado por un tipo de máquina de Turing restringida de ese tipo, y viceversa. [16]
Un transductor de estados finitos es un séxtuple , donde:
- es el alfabeto de entrada (un conjunto finito no vacío de símbolos);
- es el alfabeto de salida (un conjunto finito no vacío de símbolos);
- es un conjunto finito no vacío de estados;
- es el estado inicial, un elemento de ;
- es la función de transición de estado: ;
- es la función de salida.
Si la función de salida depende del estado y del símbolo de entrada ( ), esa definición corresponde al modelo de Mealy y puede modelarse como una máquina de Mealy . Si la función de salida depende únicamente del estado ( ), esa definición corresponde al modelo de Moore y puede modelarse como una máquina de Moore . Una máquina de estados finitos sin ninguna función de salida se conoce como semiautómata o sistema de transición .
Si ignoramos el primer símbolo de salida de una máquina de Moore, , entonces se puede convertir fácilmente a una máquina de Mealy con salida equivalente estableciendo la función de salida de cada transición de Mealy (es decir, etiquetando cada borde) con el símbolo de salida dado del estado de Moore de destino. La transformación inversa es menos sencilla porque un estado de máquina de Mealy puede tener diferentes etiquetas de salida en sus transiciones entrantes (bordes). Cada uno de esos estados debe dividirse en múltiples estados de máquina de Moore, uno para cada símbolo de salida incidente. [17]
Mejoramiento
Optimizar una FSM significa encontrar una máquina con el número mínimo de estados que realice la misma función. El algoritmo más rápido conocido que realiza esto es el algoritmo de minimización de Hopcroft . [18] [19] Otras técnicas incluyen el uso de una tabla de implicación o el procedimiento de reducción de Moore. [20] Además, las FSA acíclicas se pueden minimizar en tiempo lineal . [21]
Implementación
Aplicaciones de hardware

En un circuito digital , un FSM puede construirse utilizando un dispositivo lógico programable , un controlador lógico programable , puertas lógicas y flip flops o relés . Más específicamente, una implementación de hardware requiere un registro para almacenar variables de estado, un bloque de lógica combinacional que determina la transición de estado y un segundo bloque de lógica combinacional que determina la salida de un FSM. Una de las implementaciones de hardware clásicas es el controlador Richards .
En una máquina de Medvedev , la salida está conectada directamente a los flip-flops de estado, minimizando el retraso de tiempo entre los flip-flops y la salida. [22] [23]
A través de la codificación de estados, las máquinas de estados de bajo consumo se pueden optimizar para minimizar el consumo de energía.
Aplicaciones de software
Los siguientes conceptos se utilizan comúnmente para crear aplicaciones de software con máquinas de estados finitos:
- Programación basada en autómatas
- Máquina de estados finitos basada en eventos
- Máquina virtual de estados finitos
- Patrón de diseño de estado
Máquinas de estados finitos y compiladores
Los autómatas finitos se utilizan a menudo en la interfaz de los compiladores de lenguajes de programación. Una interfaz de este tipo puede comprender varias máquinas de estados finitos que implementan un analizador léxico y un analizador sintáctico. A partir de una secuencia de caracteres, el analizador léxico construye una secuencia de tokens de lenguaje (como palabras reservadas, literales e identificadores) a partir de la cual el analizador sintáctico construye un árbol sintáctico. El analizador léxico y el analizador sintáctico manejan las partes regulares y libres de contexto de la gramática del lenguaje de programación. [24]
Véase también
- Máquinas de estados abstractos
- Autómata finito alterno
- Máquina de estados finitos comunicante
- Sistema de control
- Mesa de control
- Tablas de decisión
- DESARROLLADORES
- Modelo oculto de Markov
- Red de Petri
- Autómata de empuje hacia abajo
- Autómata cuántico finito
- Formato XML de escala de grises
- Semiautomático
- Acción de semigrupo
- Lógica secuencial
- Diagrama de estados
- Sincronización de palabras
- Semigrupo de transformación
- Sistema de transición
- Autómata de árbol
- Máquina de Turing
- Máquina de estados UML
Referencias
- ^ Wang, Jiacun (2019). Métodos formales en informática . CRC Press. pág. 34. ISBN 978-1-4987-7532-8.
- ^ "Máquinas de estados finitos – Brilliant Math & Science Wiki". brilliant.org . Consultado el 14 de abril de 2018 .
- ^ Belzer, Jack; Holzman, Albert George; Kent, Allen (1975). Enciclopedia de informática y tecnología. Vol. 25. EE. UU.: CRC Press. pág. 73. ISBN 978-0-8247-2275-3.
- ^ ab Koshy, Thomas (2004). Matemática discreta con aplicaciones. Academic Press. pág. 762. ISBN 978-0-12-421180-3.
- ^ Wright, David R. (2005). "Finite State Machines" (PDF) . Notas de clase de CSC215 . Sitio web de David R. Wright, N. Carolina State Univ. Archivado desde el original (PDF) el 2014-03-27 . Consultado el 2012-07-14 .
- ^ ab Keller, Robert M. (2001). "Clasificadores, aceptores, transductores y secuenciadores" (PDF) . Ciencias de la computación: de la abstracción a la implementación (PDF) . Harvey Mudd College. pág. 480.
- ^ John E. Hopcroft y Jeffrey D. Ullman (1979). Introducción a la teoría de autómatas, lenguajes y computación. Lectura/MA: Addison-Wesley. ISBN 978-0-201-02988-8.
- ^ Pouly, Marc; Kohlas, Jürg (2011). Inferencia genérica: una teoría unificadora para el razonamiento automatizado . John Wiley & Sons. Capítulo 6. Álgebras de valoración para problemas de trayectorias, pág. 223 en particular. ISBN 978-1-118-01086-0.
- ^ Jacek Jonczy (junio de 2008). "Problemas de trayectorias algebraicas" (PDF) . Archivado desde el original (PDF) el 21 de agosto de 2014. Consultado el 20 de agosto de 2014 ., pág. 34
- ^ Felkin, M. (2007). Guillet, Fabrice; Hamilton, Howard J. (eds.). Medidas de calidad en minería de datos - Estudios en inteligencia computacional . Vol. 43. Springer, Berlín, Heidelberg. págs. 277–278. doi :10.1007/978-3-540-44918-8_12. ISBN 978-3-540-44911-9.
- ^ Brutscheck, M., Berger, S., Franke, M., Schwarzbacher, A., Becker, S.: Procedimiento de división estructural para un análisis eficiente de circuitos integrados. Conferencia irlandesa sobre señales y sistemas de la IET (ISSC 2008), págs. 18-23. Galway, Irlanda, 18-19 de junio de 2008. [1]
- ^ "Tiwari, A. (2002). Semántica formal y métodos de análisis para modelos de Stateflow de Simulink" (PDF) . sri.com . Consultado el 14 de abril de 2018 .
- ^ Hamon, G. (2005). Una semántica denotacional para Stateflow . Conferencia internacional sobre software integrado. Jersey City, NJ: ACM. págs. 164–172. CiteSeerX 10.1.1.89.8817 .
- ^ "Harel, D. (1987). Un formalismo visual para sistemas complejos. Science of Computer Programming, 231–274" (PDF) . Archivado desde el original (PDF) el 15 de julio de 2011. Consultado el 7 de junio de 2011 .
- ^ "Alur, R., Kanade, A., Ramesh, S., y Shashidhar, KC (2008). Análisis simbólico para mejorar la cobertura de simulación de los modelos Simulink/Stateflow. Conferencia internacional sobre software integrado (pp. 89–98). Atlanta, GA: ACM" (PDF) . Archivado desde el original (PDF) el 15 de julio de 2011.
- ^ Black, Paul E (12 de mayo de 2008). «Máquina de estados finitos». Diccionario de algoritmos y estructuras de datos . Instituto Nacional de Estándares y Tecnología de Estados Unidos . Archivado desde el original el 13 de octubre de 2018. Consultado el 2 de noviembre de 2016 .
- ^ Anderson, James Andrew; Head, Thomas J. (2006). Teoría de autómatas con aplicaciones modernas. Cambridge University Press. pp. 105–108. ISBN 978-0-521-84887-9.
- ^ Hopcroft, John E. (1971). Un algoritmo n log n para minimizar estados en un autómata finito (PDF) (Informe técnico). Vol. CS-TR-71-190. Universidad de Stanford.[ enlace muerto permanente ]
- ^ Almeida, Marco; Moreira, Nelma; Reis, Rogerio (2007). Sobre el rendimiento de algoritmos de minimización de autómatas (PDF) (Informe técnico). vol. DCC-2007-03. Universidad de Oporto. Archivado desde el original (PDF) el 17 de enero de 2009 . Consultado el 25 de junio de 2008 .
- ^ Edward F. Moore (1956). CE Shannon y J. McCarthy (ed.). "Experimentos de laboratorio en máquinas secuenciales". Anales de estudios matemáticos . 34 . Princeton University Press: 129–153.Aquí: Teorema 4, p.142.
- ^ Revuz, D. (1992). "Minimización de autómatas acíclicos en tiempo lineal". Ciencias de la computación teórica . 92 : 181–189. doi :10.1016/0304-3975(92)90142-3.
- ^ Kaeslin, Hubert (2008). "Bits de salida combinatorios y de tipo Mealy, Moore y Medvedev". Diseño de circuitos integrados digitales: desde arquitecturas VLSI hasta fabricación CMOS . Cambridge University Press. pág. 787. ISBN 978-0-521-88267-5.
- ^ Diapositivas archivadas el 18 de enero de 2017 en Wayback Machine , Máquinas de estados finitos sincrónicos: diseño y comportamiento , Universidad de Ciencias Aplicadas de Hamburgo , p.18
- ^ Aho, Alfred V. ; Sethi, Ravi ; Ullman, Jeffrey D. (1986). Compiladores: principios, técnicas y herramientas (1.ª ed.). Addison-Wesley . ISBN 978-0-201-10088-4.
Lectura adicional
General
- Sakarovitch, Jacques (2009). Elementos de la teoría de autómatas . Traducido del francés por Reuben Thomas. Cambridge University Press . ISBN 978-0-521-84425-3.Zbl1188.68177 .
- Wagner, F., "Modelado de software con máquinas de estados finitos: un enfoque práctico", Auerbach Publications, 2006, ISBN 0-8493-8086-3 .
- UIT-T, Recomendación Z.100 Lenguaje de especificación y descripción (SDL)
- Samek, M., Diagramas de estados prácticos en C/C++, CMP Books, 2002, ISBN 1-57820-110-1 .
- Samek, M., Diagramas de estados UML prácticos en C/C++, 2.ª edición, Newnes, 2008, ISBN 0-7506-8706-1 .
- Gardner, T., Gestión avanzada del estado Archivado el 19 de noviembre de 2008 en Wayback Machine , 2007
- Cassandras, C., Lafortune, S., "Introducción a los sistemas de eventos discretos". Kluwer, 1999, ISBN 0-7923-8609-4 .
- Timothy Kam, Síntesis de máquinas de estados finitos: optimización funcional . Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9842-4
- Tiziano Villa, Síntesis de máquinas de estados finitos: optimización lógica . Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9892-0
- Carroll, J., Long, D., Teoría de autómatas finitos con una introducción a los lenguajes formales . Prentice Hall, Englewood Cliffs, 1989.
- Kohavi, Z., Teoría de autómatas finitos y de conmutación . McGraw-Hill, 1978.
- Gill, A., Introducción a la teoría de máquinas de estados finitos . McGraw-Hill, 1962.
- Ginsburg, S., Introducción a la teoría matemática de máquinas . Addison-Wesley, 1962.
Máquinas de estados finitos (teoría de autómatas) en la informática teórica
- Arbib, Michael A. (1969). Teorías de autómatas abstractos (1.ª ed.). Englewood Cliffs, NJ: Prentice-Hall, Inc. ISBN 978-0-13-913368-8.
- Bobrow, Leonard S.; Arbib, Michael A. (1974). Matemáticas discretas: álgebra aplicada a la informática y la ciencia de la información (1.ª ed.). Filadelfia: WB Saunders Company, Inc. ISBN 978-0-7216-1768-8.
- Booth, Taylor L. (1967). Máquinas secuenciales y teoría de autómatas (1.ª ed.). Nueva York: John Wiley and Sons, Inc. Catálogo de fichas de la Biblioteca del Congreso, número 67-25924.
- Boolos, George; Jeffrey, Richard (1999) [1989]. Computabilidad y lógica (3.ª ed.). Cambridge, Inglaterra: Cambridge University Press. ISBN 978-0-521-20402-6.
- Brookshear, J. Glenn (1989). Teoría de la computación: lenguajes formales, autómatas y complejidad . Redwood City, California: Benjamin/Cummings Publish Company, Inc. ISBN 978-0-8053-0143-4.
- Davis, Martin; Sigal, Ron; Weyuker, Elaine J. (1994). Computabilidad, complejidad y lenguajes y lógica: fundamentos de la informática teórica (2.ª ed.). San Diego: Academic Press, Harcourt, Brace & Company. ISBN 978-0-12-206382-4.
- Hopcroft, John; Ullman, Jeffrey (1979). Introducción a la teoría de autómatas, lenguajes y computación (1.ª ed.). Reading Mass: Addison-Wesley. ISBN 978-0-201-02988-8.
- Hopcroft, John E.; Motwani, Rajeev; Ullman, Jeffrey D. (2001). Introducción a la teoría de autómatas, lenguajes y computación (2.ª ed.). Reading Mass: Addison-Wesley. ISBN 978-0-201-44124-6.
- Hopkins, David; Moss, Bárbara (1976). Autómatas . Nueva York: Elsevier Holanda Septentrional. ISBN 978-0-444-00249-5.
- Kozen, Dexter C. (1997). Autómatas y computabilidad (1ª ed.). Nueva York: Springer-Verlag. ISBN 978-0-387-94907-9.
- Lewis, Harry R. ; Papadimitriou, Christos H. (1998). Elementos de la teoría de la computación (2.ª ed.). Upper Saddle River, Nueva Jersey: Prentice-Hall. ISBN 978-0-13-262478-7.
- Linz, Peter (2006). Lenguajes formales y autómatas (4.ª ed.). Sudbury, MA: Jones y Bartlett. ISBN 978-0-7637-3798-6.
- Minsky, Marvin (1967). Computación: máquinas finitas e infinitas (1.ª ed.). Nueva Jersey: Prentice-Hall.
- Papadimitriou, Christos (1993). Complejidad computacional (1.ª ed.). Addison Wesley. ISBN 978-0-201-53082-7.
- Pippenger, Nicholas (1997). Teorías de la computabilidad (1.ª ed.). Cambridge, Inglaterra: Cambridge University Press. ISBN 978-0-521-55380-3.
- Rodger, Susan; Finley, Thomas (2006). JFLAP: Un paquete interactivo de lenguajes formales y autómatas (1.ª ed.). Sudbury, MA: Jones y Bartlett. ISBN 978-0-7637-3834-1.
- Sipser, Michael (2006). Introducción a la teoría de la computación (2.ª ed.). Boston, Mass.: Thomson Course Technology. ISBN 978-0-534-95097-2.
- Wood, Derick (1987). Teoría de la computación (1.ª ed.). Nueva York: Harper & Row, Publishers, Inc. ISBN 978-0-06-047208-5.
Máquinas de estados abstractos en la informática teórica
- Gurevich, Yuri (julio de 2000). "Máquinas de estados abstractos secuenciales capturan algoritmos secuenciales" (PDF) . ACM Transactions on Computational Logic . 1 (1): 77–111. CiteSeerX 10.1.1.146.3017 . doi :10.1145/343369.343384. S2CID 2031696.
Aprendizaje automático mediante algoritmos de estados finitos
- Mitchell, Tom M. (1997). Aprendizaje automático (1.ª ed.). Nueva York: WCB/McGraw-Hill Corporation. ISBN 978-0-07-042807-2.
Ingeniería de hardware: minimización de estados y síntesis de circuitos secuenciales
- Booth, Taylor L. (1967). Máquinas secuenciales y teoría de autómatas (1.ª ed.). Nueva York: John Wiley and Sons, Inc. Catálogo de fichas de la Biblioteca del Congreso, número 67-25924.
- Booth, Taylor L. (1971). Redes digitales y sistemas informáticos (1.ª ed.). Nueva York: John Wiley and Sons, Inc. ISBN 978-0-471-08840-0.
- McCluskey, EJ (1965). Introducción a la teoría de circuitos de conmutación (1.ª ed.). Nueva York: McGraw-Hill Book Company, Inc. Catálogo de fichas de la Biblioteca del Congreso, número 65-17394.
- Hill, Fredrick J.; Peterson, Gerald R. (1965). Introducción a la teoría de circuitos de conmutación (1.ª ed.). Nueva York: McGraw-Hill Book Company. Catálogo de fichas de la Biblioteca del Congreso, número 65-17394.
Procesos de cadena de Markov finitos
- "Podemos pensar en una cadena de Markov como un proceso que se mueve sucesivamente a través de un conjunto de estados s 1 , s 2 , …, s r . … si está en el estado s i pasa a la siguiente parada al estado s j con probabilidad p ij . Estas probabilidades pueden presentarse en forma de una matriz de transición" (Kemeny (1959), p. 384)
Los procesos de cadenas de Markov finitas también se conocen como subdesplazamientos de tipo finito .
- Booth, Taylor L. (1967). Máquinas secuenciales y teoría de autómatas (1.ª ed.). Nueva York: John Wiley and Sons, Inc. Catálogo de fichas de la Biblioteca del Congreso, número 67-25924.
- Kemeny, John G.; Mirkil, Hazleton; Snell, J. Laurie; Thompson, Gerald L. (1959). Estructuras matemáticas finitas (1.ª ed.). Englewood Cliffs, NJ: Prentice-Hall, Inc. Catálogo de fichas de la Biblioteca del Congreso, número 59-12841.Capítulo 6 "Cadenas de Markov finitas".
Enlaces externos
- Modelado de un comportamiento de IA simple utilizando una máquina de estados finitos Ejemplo de uso en videojuegos
- Diccionario gratuito en línea de computación Descripción de máquinas de estados finitos
- Diccionario NIST de algoritmos y estructuras de datos Descripción de máquinas de estados finitos
- Una breve descripción general de los tipos de máquinas de estados, comparando aspectos teóricos de las máquinas de estados Mealy, Moore, Harel y UML.




















