Fotoelasticidad

This article needs additional citations for verification. (September 2022) |
En la ciencia de los materiales , la fotoelasticidad describe los cambios en las propiedades ópticas de un material bajo deformación mecánica . Es una propiedad de todos los medios dieléctricos y se utiliza a menudo para determinar experimentalmente la distribución de la tensión en un material.
Historia
El fenómeno fotoelástico fue descubierto por primera vez por el físico escocés David Brewster , quien inmediatamente lo reconoció como birrefringencia inducida por estrés . [1] [2] Ese diagnóstico fue confirmado en un experimento de refracción directa por Augustin-Jean Fresnel . [3] Los marcos experimentales se desarrollaron a principios del siglo XX con los trabajos de EG Coker y LNG Filon de la Universidad de Londres . Su libro Treatise on Photoelasticity , publicado en 1930 por Cambridge Press , se convirtió en un texto estándar sobre el tema. Entre 1930 y 1940, aparecieron muchos otros libros sobre el tema, incluidos libros en ruso, alemán y francés. Max M. Frocht publicó el trabajo clásico de dos volúmenes, Photoelasticity , en el campo. [4] Al mismo tiempo, se produjo un gran desarrollo en el campo: se lograron grandes mejoras en la técnica y se simplificó el equipo. Con los refinamientos en la tecnología, los experimentos fotoelásticos se extendieron a la determinación de estados tridimensionales de estrés. Paralelamente a los avances en la técnica experimental, la primera descripción fenomenológica de la fotoelasticidad fue dada en 1890 por Friedrich Pockels [5] , sin embargo, esta fue demostrada como inadecuada casi un siglo después por Nelson y Lax [6] ya que la descripción de Pockels sólo consideraba el efecto de la tensión mecánica sobre las propiedades ópticas del material.
Con la aparición del polariscopio digital , posible gracias a los diodos emisores de luz, se hizo posible el control continuo de estructuras bajo carga, lo que condujo al desarrollo de la fotoelasticidad dinámica, que ha contribuido en gran medida al estudio de fenómenos complejos como la fractura de materiales.
Aplicaciones

La fotoelasticidad se ha utilizado para una variedad de análisis de tensión e incluso para uso rutinario en diseño, particularmente antes de la llegada de métodos numéricos, como elementos finitos o elementos de contorno . [7] La digitalización de la polariscopía permite la adquisición rápida de imágenes y el procesamiento de datos, lo que permite sus aplicaciones industriales para controlar la calidad del proceso de fabricación de materiales como el vidrio [8] y el polímero. [9] La odontología utiliza la fotoelasticidad para analizar la tensión en los materiales de las dentaduras postizas. [10]
La fotoelasticidad se puede utilizar con éxito para investigar el estado de tensión altamente localizado dentro de la mampostería [11] [12] [13] o en la proximidad de una inclusión de línea rígida (refuerzo) incrustada en un medio elástico. [14] En el primer caso, el problema no es lineal debido a los contactos entre ladrillos, mientras que en el segundo caso la solución elástica es singular, por lo que los métodos numéricos pueden no proporcionar resultados correctos. Estos se pueden obtener mediante técnicas fotoelásticas. La fotoelasticidad dinámica integrada con fotografía de alta velocidad se utiliza para investigar el comportamiento de fractura en materiales. [15] Otra aplicación importante de los experimentos de fotoelasticidad es estudiar el campo de tensión alrededor de entalladuras bimateriales. [16] Las entalladuras bimateriales existen en muchas aplicaciones de ingeniería como estructuras soldadas o unidas mediante adhesivos. [ cita requerida ]
Por ejemplo, algunos elementos de las catedrales góticas que anteriormente se consideraban decorativos se demostraron esenciales para el soporte estructural mediante métodos fotoelásticos. [17]
Definición formal
Para un material dieléctrico lineal, el cambio en el tensor de permitividad inversa con respecto a la deformación (el gradiente del desplazamiento ) se describe mediante [18]
donde es el tensor de fotoelasticidad de cuarto rango, es el desplazamiento lineal desde el equilibrio y denota diferenciación con respecto a la coordenada cartesiana . Para materiales isotrópicos, esta definición se simplifica a [19]
donde es la parte simétrica del tensor fotoelástico (el tensor de deformación fotoelástica), y es la deformación lineal . La parte antisimétrica de se conoce como tensor roto-óptico. De cualquiera de las definiciones, es claro que las deformaciones del cuerpo pueden inducir anisotropía óptica, que puede hacer que un material ópticamente isótropo presente birrefringencia . Aunque el tensor fotoelástico simétrico se define más comúnmente con respecto a la deformación mecánica, también es posible expresar la fotoelasticidad en términos de la tensión mecánica .
Principios experimentales

El procedimiento experimental se basa en la propiedad de birrefringencia , que presentan ciertos materiales transparentes. La birrefringencia es un fenómeno en el que un rayo de luz que pasa a través de un material determinado experimenta dos índices de refracción . La propiedad de birrefringencia (o doble refracción) se observa en muchos cristales ópticos . Al aplicar tensiones, los materiales fotoelásticos presentan la propiedad de birrefringencia, y la magnitud de los índices de refracción en cada punto del material está directamente relacionada con el estado de las tensiones en ese punto. Se puede obtener información como la tensión cortante máxima y su orientación analizando la birrefringencia con un instrumento llamado polariscopio .
Cuando un rayo de luz pasa a través de un material fotoelástico, sus componentes de onda electromagnética se resuelven a lo largo de las dos direcciones de tensión principales y cada componente experimenta un índice de refracción diferente debido a la birrefringencia. La diferencia en los índices de refracción conduce a un retardo de fase relativo entre los dos componentes. Suponiendo una muestra delgada hecha de materiales isotrópicos , donde es aplicable la fotoelasticidad bidimensional, la magnitud del retardo relativo viene dada por la ley de tensión-óptica : [20]
donde Δ es el retardo inducido, C es elcoeficiente de tensión óptica ,tes el espesor de la muestra,λes la longitud de onda del vacío yσ1yσ2son la primera y la segunda tensión principal, respectivamente. La retardación cambia la polarización de la luz transmitida. El polariscopio combina los diferentes estados de polarización de las ondas de luz antes y después de pasar por la muestra. Debido ala interferenciade las dos ondas, se revela un patrón de franjas. El número de orden de franjaNse denota como
que depende del retardo relativo. Al estudiar el patrón de franjas se puede determinar el estado de tensión en varios puntos del material.
En el caso de materiales que no presentan un comportamiento fotoelástico, aún es posible estudiar la distribución de tensiones. El primer paso es construir un modelo, utilizando materiales fotoelásticos, que tenga una geometría similar a la estructura real que se está investigando. Luego, se aplica la carga de la misma manera para garantizar que la distribución de tensiones en el modelo sea similar a la tensión en la estructura real.
Isocilinas e isocromaticas
Las isoclínicas son los lugares de los puntos de la muestra a lo largo de los cuales las tensiones principales están en la misma dirección. [ cita requerida ]
Las isocromáticas son los lugares geométricos en los que la diferencia entre la primera y la segunda tensión principal permanece igual. Por lo tanto, son las líneas que unen los puntos con la misma magnitud de tensión cortante máxima. [21]
Fotoelasticidad bidimensional

La fotoelasticidad puede describir estados de tensión tanto tridimensionales como bidimensionales. Sin embargo, examinar la fotoelasticidad en sistemas tridimensionales es más complejo que en sistemas bidimensionales o de tensión plana. Por lo tanto, la presente sección trata de la fotoelasticidad en un sistema de tensión plana. Esta condición se logra cuando el espesor del prototipo es mucho menor en comparación con las dimensiones en el plano. [ cita requerida ] Por lo tanto, solo se preocupan las tensiones que actúan paralelas al plano del modelo, ya que los demás componentes de la tensión son cero. La configuración experimental varía de un experimento a otro. Los dos tipos básicos de configuración utilizados son el polariscopio plano y el polariscopio circular. [ cita requerida ]
El principio de funcionamiento de un experimento bidimensional permite medir el retardo, que se puede convertir en la diferencia entre la primera y la segunda tensión principal y su orientación. Para obtener más valores de cada componente de tensión, se requiere una técnica llamada separación de tensiones. [22] Se utilizan varios métodos teóricos y experimentales para proporcionar información adicional para resolver los componentes de tensión individuales.
Configuración del polariscopio plano
El equipo consta de dos polarizadores lineales y una fuente de luz. La fuente de luz puede emitir luz monocromática o luz blanca, según el experimento. Primero, la luz pasa a través del primer polarizador, que la convierte en luz polarizada plana. El aparato está configurado de tal manera que esta luz polarizada plana pasa a través de la muestra sometida a tensión. Esta luz sigue, en cada punto de la muestra, la dirección de la tensión principal en ese punto. Luego, la luz pasa a través del analizador y finalmente obtenemos el patrón de franjas. [ cita requerida ]
El patrón de franjas en una configuración de polariscopio plano consta tanto de isocromaticas como de isoclinas. Las isoclinas cambian con la orientación del polariscopio, mientras que no hay cambios en las isocromaticas. [ cita requerida ]
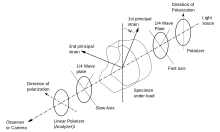
El mismo dispositivo funciona como un polariscopio plano cuando las placas de cuarto de onda se separan o se giran de modo que sus ejes queden paralelos a los ejes de polarización.
Configuración del polariscopio circular
En una configuración de polariscopio circular, se añaden dos placas de cuarto de onda a la configuración experimental del polariscopio plano. La primera placa de cuarto de onda se coloca entre el polarizador y la muestra y la segunda placa de cuarto de onda se coloca entre la muestra y el analizador. El efecto de añadir la placa de cuarto de onda después del polarizador del lado de la fuente es que obtenemos luz polarizada circularmente que pasa a través de la muestra. La placa de cuarto de onda del lado del analizador convierte el estado de polarización circular de nuevo en lineal antes de que la luz pase a través del analizador. [ cita requerida ]
La ventaja básica de un polariscopio circular sobre un polariscopio plano es que en una configuración de polariscopio circular solo obtenemos las isocrómicas y no las isoclínicas. Esto elimina el problema de diferenciar entre las isoclínicas y las isocrómicas. [ cita requerida ]
Véase también
Referencias
- ^ Brewster, David (1815). "Experimentos sobre la despolarización de la luz tal como se manifiesta en diversos cuerpos minerales, animales y vegetales, con una referencia de los fenómenos a los principios generales de polarización". Philosophical Transactions of the Royal Society of London . 105 : 29–53. doi : 10.1098/rstl.1815.0004 .
- ^ Brewster, David (1816). "Sobre la comunicación de la estructura de cristales birrefractores al vidrio, muriato de sodio, espato flúor y otras sustancias, por compresión mecánica y dilatación". Philosophical Transactions of the Royal Society of London . 106 : 156–78. doi :10.1098/rstl.1816.0011. S2CID 108782967.
- ^ Fresnel, Agustín (1822). "Note sur la double réfraction du verre comprimé". Annales de Chimie et de Physique . Serie 2. 20 : 376–83.
- Reimpreso en H. de Senarmont, E. Verdet y L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel , vol. 1 (1866), págs. 713–18
- Traducido como Fresnel, Augustin-Jean (2021). "Nota sobre la doble refracción del vidrio comprimido". Traducido por Putland, Gavin Richard. doi :10.5281/zenodo.4706835.
{{cite journal}}: Requiere citar revista|journal=( ayuda )
- ^ Leven, MM; Frocht, MM, eds. (1969). "Vita Max Mark Frocht". Fotoelasticidad . Pérgamo. págs. xi-xii. doi :10.1016/B978-0-08-012998-3.50005-7. ISBN 978-0-08-012998-3.
- ^ Pockels, F. (1890). "Ueber die durch einseitigen Druck hervorgerufene Doppelbrechung regulärer Krystalle, speciell von Steinsalz und Sylvin". Annalen der Physik und Chemie . 275 (3): 440–69. Código bibliográfico : 1890AnP...275..440P. doi : 10.1002/andp.18902750313.
- ^ Nelson, DF; Lax, M. (1970). "Nueva simetría para dispersión acústico-óptica". Physical Review Letters . 24 (8): 379–80. Código Bibliográfico :1970PhRvL..24..379N. doi :10.1103/PhysRevLett.24.379.
- ^ Frocht, MM, Fotoelasticidad . J. Wiley and Sons, Londres, 1965.
- ^ Ajovalasit, A.; Petrucci, G.; Scafidi, M. (2012). "Fotoelasticidad RGB aplicada al análisis de la tensión residual de membrana en vidrio". Measurement Science and Technology . 23 (2): 025601. Bibcode :2012MeScT..23b5601A. doi :10.1088/0957-0233/23/2/025601. hdl : 10447/61842 . S2CID 53600215.
- ^ Kramer, Sharlotte; Beiermann, Brett; Davis, Douglas; Sottos, Nancy; White, Scott; Moore, Jeffrey (2013). "Caracterización de polímeros mecanoquímicamente activos mediante mediciones combinadas de fotoelasticidad y fluorescencia". Aplicación de técnicas de imagenología a la mecánica de materiales y estructuras, volumen 4. Actas de congresos de la serie Society for Experimental Mechanics. págs. 167–78. doi :10.1007/978-1-4419-9796-8_21. ISBN 978-1-4419-9528-5.
- ^ Fernandes, Cláudio P.; Glantz, Per-Olof J.; Svensson, Stig A.; Bergmark, Anders (2003). "Fotoelasticidad de reflexión: un nuevo método para estudios de mecánica clínica en odontología protésica". Materiales dentales . 19 (2): 106–17. doi :10.1016/s0109-5641(02)00019-2. PMID 12543116.
- ^ Bigoni, Davide; Noselli, Giovanni (2010). "Percolación de tensiones localizadas a través de muros de mampostería seca. Parte I – Experimentos". Revista Europea de Mecánica - A/Sólidos . 29 (3): 291–98. Código Bibliográfico :2010EuJMA..29..291B. doi :10.1016/j.euromechsol.2009.10.009.
- ^ Bigoni, Davide; Noselli, Giovanni (2010). "Percolación de tensiones localizadas a través de muros de mampostería seca. Parte II – Modelado". Revista Europea de Mecánica – A/Sólidos . 29 (3): 299–307. Código Bibliográfico :2010EuJMA..29..299B. doi :10.1016/j.euromechsol.2009.10.013.
- ^ Bigoni, D. (2012). Mecánica de sólidos no lineales: teoría de bifurcación e inestabilidad de los materiales . Cambridge University Press. ISBN 9781107025417.
- ^ Noselli, G.; Dal Corso, F.; Bigoni, D. (2010). "La intensidad de la tensión cerca de un rigidizador revelada por la fotoelasticidad". Revista Internacional de Fractura . 166 (1–2): 91–103. doi :10.1007/s10704-010-9502-9. S2CID 56221414.
- ^ Shukla, A. (2001). "Estudios de fracturas a alta velocidad en interfaces bimateriales utilizando fotoelasticidad: una revisión". The Journal of Strain Analysis for Engineering Design . 36 (2): 119–42. doi :10.1243/0309324011512658. S2CID 137504535.
- ^ Ayatollahi, MR; Mirsayar, MM; Dehghany, M. (2011). "Determinación experimental de parámetros de campo de tensión en muescas bimateriales utilizando fotoelasticidad". Materiales y diseño . 32 (10): 4901–08. doi :10.1016/j.matdes.2011.06.002.
- ^ Lewis, Michael (3 de septiembre de 2024). "The Canary: Michael Lewis habla de Chris Mark, del Departamento de Trabajo". The Washington Post .
- ^ JF Nye, Propiedades físicas de los cristales: su representación mediante tensores y matrices , Oxford University Press, 1957. [ ISBN faltante ] [ página necesaria ]
- ^ RE Newnham, Propiedades de los materiales: anisotropía, simetría, estructura , Oxford University Press, 2005. [ ISBN faltante ] [ página necesaria ]
- ^ Dally, JW y Riley, WF, Experimental Stress Analysis, 3.ª ed., McGraw-Hill Inc., 1991 [ ISBN faltante ] [ página necesaria ]
- ^ Ramesh, K., Fotoelasticidad digital, Springer, 2000 [ ISBN faltante ] [ página necesaria ]
- ^ Solaguren-Beascoa Fernández, M.; Alegre Calderón, JM; Bravo Díez, PM; Cuesta Segura, II (2010). "Técnicas de separación de tensiones en fotoelasticidad: una revisión". La revista de análisis de deformaciones para el diseño de ingeniería . 45 : 1–17. doi :10.1243/03093247JSA583. S2CID 208518298.
Enlaces externos
- Página de la Universidad de Cambridge sobre fotoelasticidad.
- Laboratorio de Modelado Físico de Estructuras y Fotoelasticidad (Universidad de Trento, Italia)
- Construye tu propio polariscopio












