Luna (geometría)

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Lune» geometría – noticias  · periódicos  · libros  · académico  · JSTOR ( julio de 2021 ) ( Aprenda cómo y cuándo eliminar este mensaje )

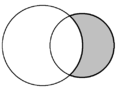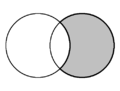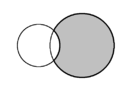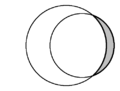
En geometría plana, la forma de medialuna formada por dos círculos que se cortan se denomina luna . En cada diagrama hay dos lunas y una está sombreada en gris.

En geometría plana , una lúnula (del latín luna,  «luna») es la región cóncava-convexa delimitada por dos arcos circulares . ^[1] Tiene una porción límite en la que el segmento de conexión de dos puntos cercanos cualesquiera se mueve fuera de la región y otra porción límite en la que el segmento de conexión de dos puntos cercanos cualesquiera se encuentra completamente dentro de la región. Una región convexa-convexa se denomina lente . ^[2]

Formalmente, una luna es el complemento relativo de un disco en otro (donde se intersecan pero ninguno es un subconjunto del otro). Alternativamente, si y son discos, entonces es una luna.${\estilo de visualización A}$${\estilo de visualización B}$${\displaystyle A\smallsetminus A\cap B}$

En el siglo V a. C., Hipócrates de Quíos demostró que la Luna de Hipócrates y otras dos lunas podían ser exactamente cuadradas (convertidas en un cuadrado con la misma área) mediante regla y compás . En 1766, el matemático finlandés Daniel Wijnquist, citando a Daniel Bernoulli , enumeró las cinco lunas geométricas cuadrables, agregando a las conocidas por Hipócrates. En 1771, Leonhard Euler dio un enfoque general y obtuvo una cierta ecuación para el problema. En 1933 y 1947, Nikolai Chebotaryov y su estudiante Anatoly Dorodnov demostraron que estas cinco son las únicas lunas cuadrables. ^{[3] [1]}

El área de una luna formada por círculos de radios a y b ( b>a ) con distancia c entre sus centros es ^[3]

${\displaystyle A=2\Delta +a^{2}\sec ^{-1}\left({\frac {2ac}{b^{2}-a^{2}-c^{2}}}\right)-b^{2}\sec ^{-1}\left({\frac {2bc}{b^{2}+c^{2}-a^{2}}}\right),}$

donde es la función inversa de la función secante , y donde ${\displaystyle {\text{seg}}^{-1}}$

${\displaystyle \Delta ={\frac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+bc)}}}$

es el área de un triángulo con lados a, b y c .

• Arbelos
• Creciente
• Teorema de Gauss-Bonnet
• Lente

• Los cinco lunares cuadrangulares en MathPages