Función lineal (cálculo)

A este artículo le falta información sobre el caso de funciones multivariadas y funciones con valores vectoriales, que deben tenerse en cuenta, ya que este artículo está vinculado a Matriz jacobiana . Amplíe el artículo para incluir esta información. Puede que existan más detalles en la página de discusión . ( Febrero de 2020 )

En cálculo y áreas relacionadas de las matemáticas, una función lineal de los números reales a los números reales es una función cuyo gráfico (en coordenadas cartesianas ) es una línea no vertical en el plano. ^[1] La propiedad característica de las funciones lineales es que cuando se cambia la variable de entrada, el cambio en la salida es proporcional al cambio en la entrada.

Las funciones lineales están relacionadas con ecuaciones lineales .

Una función lineal es una función polinómica en la que la variable x tiene grado como máximo uno: ^[2]

${\displaystyle f(x)=ax+b}$.

Una función de este tipo se denomina lineal porque su gráfica , el conjunto de todos los puntos del plano cartesiano , es una recta . El coeficiente a se denomina pendiente de la función y de la recta (véase más abajo).${\estilo de visualización (x,f(x))}$

Si la pendiente es , se trata de una función constante que define una línea horizontal, que algunos autores excluyen de la clase de funciones lineales. ^[3] Con esta definición, el grado de un polinomio lineal sería exactamente uno, y su gráfica sería una línea que no es ni vertical ni horizontal. Sin embargo, en este artículo se requiere, por lo que las funciones constantes se considerarán lineales.${\estilo de visualización a=0}$ ${\displaystyle f(x)=b}$${\displaystyle a\neq 0}$

Si entonces se dice que la función lineal es homogénea . Tal función define una línea que pasa por el origen del sistema de coordenadas, es decir, el punto . En los textos de matemáticas avanzadas, el término función lineal a menudo denota funciones lineales específicamente homogéneas, mientras que el término función afín se utiliza para el caso general, que incluye .${\estilo de visualización b=0}$${\displaystyle (x,y)=(0,0)}$${\estilo de visualización b\neq 0}$

El dominio natural de una función lineal , el conjunto de valores de entrada permitidos para x , es el conjunto entero de números reales . También se pueden considerar tales funciones con x en un campo arbitrario , tomando los coeficientes a, b en ese campo.${\estilo de visualización f(x)}$${\displaystyle x\in \mathbb {R} .}$

La gráfica es una línea no vertical que tiene exactamente una intersección con el eje y , su punto de intersección con el eje y El valor de la intersección con el eje y también se denomina valor inicial de Si la gráfica es una línea no horizontal que tiene exactamente una intersección con el eje x , el punto de intersección con el eje x El valor de la intersección con el eje x la solución de la ecuación también se denomina raíz o cero de${\displaystyle y=f(x)=ax+b}$${\displaystyle (x,y)=(0,b).}$${\displaystyle y=f(0)=b}$${\estilo de visualización f(x).}$${\displaystyle a\neq 0,}$${\displaystyle (x,y)=(-{\tfrac {b}{a}},0).}$${\displaystyle x=-{\frac {b}{a}},}$${\displaystyle f(x)=0,}$${\estilo de visualización f(x).}$

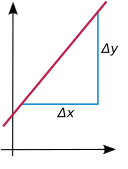
La pendiente de una línea no vertical es un número que mide cuán inclinada está la línea (elevación-recorrido). Si la línea es el gráfico de la función lineal , esta pendiente está dada por la constante a .${\displaystyle f(x)=ax+b}$

La pendiente mide la tasa constante de cambio por unidad de cambio en x : siempre que la entrada x se incrementa en una unidad, la salida cambia en una unidad: , y más generalmente para cualquier número . Si la pendiente es positiva, , entonces la función es creciente; si , entonces es decreciente${\estilo de visualización f(x)}$${\displaystyle f(x{+}1)=f(x)+a}$${\displaystyle f(x{+}\Delta x)=f(x)+a\Delta x}$${\displaystyle \Delta x}$${\displaystyle a>0}$${\estilo de visualización f(x)}$${\estilo de visualización a<0}$${\estilo de visualización f(x)}$

En cálculo , la derivada de una función general mide su tasa de cambio. Una función lineal tiene una tasa de cambio constante igual a su pendiente a , por lo que su derivada es la función constante .${\displaystyle f(x)=ax+b}$${\displaystyle f\,'(x)=a}$

La idea fundamental del cálculo diferencial es que cualquier función suave (no necesariamente lineal) puede aproximarse estrechamente cerca de un punto dado mediante una única función lineal. La derivada es la pendiente de esta función lineal, y la aproximación es: para . El gráfico de la aproximación lineal es la línea tangente del gráfico en el punto . La pendiente de la derivada generalmente varía con el punto c . Las funciones lineales se pueden caracterizar como las únicas funciones reales cuya derivada es constante: si para todo x , entonces para .${\estilo de visualización f(x)}$${\displaystyle x=c}$ ${\displaystyle f\,'(c)}$${\displaystyle f(x)\approx f\,'(c)(x{-}c)+f(c)}$${\displaystyle x\aproximadamente c}$${\displaystyle y=f(x)}$${\estilo de visualización (c,f(c))}$${\displaystyle f\,'(c)}$${\displaystyle f\,'(x)=a}$${\displaystyle f(x)=ax+b}$${\displaystyle b=f(0)}$

Una función lineal dada se puede escribir en varias fórmulas estándar que muestran sus diversas propiedades. La más simple es la forma pendiente-ordenada al origen : ${\estilo de visualización f(x)}$

${\displaystyle f(x)=ax+b}$,

desde donde se puede ver inmediatamente la pendiente a y el valor inicial , que es la intersección con el eje y del gráfico .${\displaystyle f(0)=b}$${\displaystyle y=f(x)}$

Dada una pendiente a y un valor conocido , escribimos la forma punto-pendiente : ${\displaystyle f(x_{0})=y_{0}}$

${\displaystyle f(x)=a(x{-}x_{0})+y_{0}}$.

En términos gráficos, esto da la línea con pendiente a que pasa por el punto .${\displaystyle y=f(x)}$${\displaystyle (x_{0},y_{0})}$

La forma de dos puntos comienza con dos valores conocidos y . Se calcula la pendiente y se la inserta en la forma de punto-pendiente: ${\displaystyle f(x_{0})=y_{0}}$${\displaystyle f(x_{1})=y_{1}}$${\displaystyle a={\tfrac {y_{1}-y_{0}}{x_{1}-x_{0}}}}$

${\displaystyle f(x)={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}(x{-}x_{0}\!)+y_{0}}$.

Su gráfica es la única recta que pasa por los puntos . La ecuación también puede escribirse para enfatizar la pendiente constante:${\displaystyle y=f(x)}$${\displaystyle (x_{0},y_{0}\!),(x_{1},y_{1}\!)}$${\displaystyle y=f(x)}$

${\displaystyle {\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}} }$.

Las funciones lineales surgen comúnmente de problemas prácticos que involucran variables con una relación lineal, es decir, que obedecen una ecuación lineal . Si , se puede resolver esta ecuación para y , obteniendo${\estilo de visualización x,y}$ ${\displaystyle Ax+By=C}$${\displaystyle B\neq 0}$

${\displaystyle y=-{\frac {A}{B}}x+{\frac {C}{B}}=ax+b,}$

donde denotamos y . Es decir, se puede considerar y como una variable dependiente (salida) obtenida a partir de la variable independiente (entrada) x mediante una función lineal: . En el plano de coordenadas xy , los posibles valores de forman una línea, la gráfica de la función . Si en la ecuación original, la línea resultante es vertical, y no se puede escribir como .${\displaystyle a=-{\frac {A}{B}}}$${\displaystyle b={\tfrac {C}{B}}}$${\displaystyle y=f(x)=ax+b}$${\estilo de visualización (x,y)}$${\estilo de visualización f(x)}$${\estilo de visualización B=0}$${\displaystyle x={\frac {C}{A}}}$${\displaystyle y=f(x)}$

Las características del gráfico se pueden interpretar en términos de las variables x e y . La intersección con el eje y es el valor inicial en . La pendiente a mide la tasa de cambio de la salida y por unidad de cambio en la entrada x . En el gráfico, mover una unidad hacia la derecha (incrementar x en 1) mueve el valor y hacia arriba en a : es decir, . La pendiente negativa a indica una disminución en y por cada aumento en x .${\displaystyle y=f(x)=ax+b}$${\displaystyle y=f(0)=b}$${\displaystyle x=0}$${\displaystyle f(x{+}1)=f(x)+a}$

Por ejemplo, la función lineal tiene pendiente , punto de intersección con el eje y y punto de intersección con el eje x .${\displaystyle y=-2x+4}$${\displaystyle a=-2}$${\displaystyle (0,b)=(0,4)}$${\estilo de visualización (2,0)}$

Supongamos que el salami y las salchichas cuestan 6 y 3 euros el kilo, y queremos comprar 12 euros. ¿Cuánto podemos comprar de cada uno? Si x kilogramos de salami e y kilogramos de salchichas cuestan un total de 12 euros, entonces, 6 euros × x + 3 euros × y = 12 euros. Resolviendo y obtenemos la forma punto-pendiente , como la anterior. Es decir, si primero elegimos la cantidad de salami x , la cantidad de salchichas se puede calcular como una función . Como el salami cuesta el doble que las salchichas, añadir un kilo de salami disminuye la salchicha en 2 kilos: , y la pendiente es −2. El punto de intersección con el eje y corresponde a comprar solo 4 kg de salchicha; mientras que el punto de intersección con el eje x corresponde a comprar solo 2 kg de salami.${\displaystyle y=-2x+4}$${\displaystyle y=f(x)=-2x+4}$${\displaystyle f(x{+}1)=f(x)-2}$${\displaystyle (x,y)=(0,4)}$${\displaystyle (x,y)=(2,0)}$

Nótese que el gráfico incluye puntos con valores negativos de x o y , que no tienen significado en términos de las variables originales (a menos que imaginemos vender carne al carnicero). Por lo tanto, deberíamos restringir nuestra función al dominio .${\displaystyle f(x)}$${\displaystyle 0\leq x\leq 2}$

También podríamos elegir y como variable independiente y calcular x mediante la función lineal inversa : sobre el dominio .${\displaystyle x=g(y)=-{\tfrac {1}{2}}y+2}$${\displaystyle 0\leq y\leq 4}$

Si el coeficiente de la variable no es cero ( a ≠ 0 ), entonces una función lineal se representa mediante un polinomio de grado 1 (también llamado polinomio lineal ), de lo contrario es una función constante – también una función polinómica, pero de grado cero.

Una línea recta, cuando se dibuja en un sistema de coordenadas diferente, puede representar otras funciones.

Por ejemplo, puede representar una función exponencial cuando sus valores se expresan en la escala logarítmica . Significa que cuando log ( g ( x )) es una función lineal de x , la función g es exponencial. Con funciones lineales, aumentar la entrada en una unidad hace que la salida aumente en una cantidad fija, que es la pendiente de la gráfica de la función. Con funciones exponenciales, aumentar la entrada en una unidad hace que la salida aumente en un múltiplo fijo, que se conoce como la base de la función exponencial.

Si tanto los argumentos como los valores de una función están en la escala logarítmica (es decir, cuando log ( y ) es una función lineal de log ( x ) ), entonces la línea recta representa una ley de potencia :

${\displaystyle \log _{r}y=a\log _{r}x+b\quad \Rightarrow \quad y=r^{b}\cdot x^{a}}$

Por otra parte, la gráfica de una función lineal en términos de coordenadas polares :

${\displaystyle r=f(\theta )=a\theta +b}$

es una espiral de Arquímedes si y un círculo en caso contrario.${\displaystyle a\neq 0}$

• Mapa afín , una generalización
• Progresión aritmética , una función lineal de argumento entero

• Stewart, James (2012), Cálculo: trascendentales tempranos (7.ª ed.), Brooks/Cole, ISBN 978-0-538-49790-9
• Swokowski, Earl W. (1983), Cálculo con geometría analítica (edición alternativa), Boston: Prindle, Weber & Schmidt, ISBN 0871503417

• https://web.archive.org/web/20130524101825/http://www.math.okstate.edu/~noell/ebsm/linear.html
• https://web.archive.org/web/20180722042342/https://corestandards.org/assets/CCSSI_Math%20Standards.pdf