Ley de Darcy

La ley de Darcy es una ecuación que describe el flujo de un fluido a través de un medio poroso y a través de una celda de Hele-Shaw . La ley fue formulada por Henry Darcy basándose en los resultados de experimentos ^[1] sobre el flujo de agua a través de lechos de arena , formando la base de la hidrogeología , una rama de las ciencias de la tierra . Es análoga a la ley de Ohm en electrostática, relacionando linealmente el caudal volumétrico del fluido con la diferencia de carga hidráulica (que a menudo es simplemente proporcional a la diferencia de presión) a través de la conductividad hidráulica . De hecho, la ley de Darcy es un caso especial de la ecuación de Stokes para el flujo de momento , que a su vez deriva de la ecuación de momento de Navier-Stokes .

La ley de Darcy fue determinada por primera vez experimentalmente por Darcy, pero desde entonces se ha derivado de las ecuaciones de Navier-Stokes mediante métodos de homogeneización . ^{[2] [3]} Es análoga a la ley de Fourier en el campo de la conducción de calor , la ley de Ohm en el campo de las redes eléctricas y la ley de Fick en la teoría de la difusión .

Una aplicación de la ley de Darcy es el análisis del flujo de agua a través de un acuífero ; la ley de Darcy junto con la ecuación de conservación de masa se simplifica a la ecuación de flujo de agua subterránea , una de las relaciones básicas de la hidrogeología .

Morris Muskat ^[4] fue el primero en refinar la ecuación de Darcy para un flujo monofásico al incluir la viscosidad en la ecuación de Darcy de una sola fase (fluida). Se puede entender que los fluidos viscosos tienen más dificultad para atravesar un medio poroso que los fluidos menos viscosos. Este cambio lo hizo adecuado para los investigadores de la industria petrolera. Basándose en los resultados experimentales de sus colegas Wyckoff y Botset, Muskat y Meres también generalizaron la ley de Darcy para cubrir un flujo multifásico de agua, petróleo y gas en el medio poroso de un yacimiento de petróleo . Las ecuaciones de flujo multifásico generalizadas de Muskat y otros proporcionan la base analítica para la ingeniería de yacimientos que existe hasta el día de hoy.

En su forma integral, la ley de Darcy, tal como la refinó Morris Muskat , en ausencia de fuerzas gravitacionales y en un medio homogéneamente permeable, se da mediante una relación de proporcionalidad simple entre el caudal volumétrico y la caída de presión a través de un medio poroso . La constante de proporcionalidad está vinculada a la permeabilidad del medio, la viscosidad dinámica del fluido , la distancia dada sobre la cual se calcula la caída de presión y el área de la sección transversal , en la forma:${\estilo de visualización Q}$ ${\displaystyle \Delta p}$ ${\estilo de visualización k}$${\estilo de visualización \mu}$${\estilo de visualización L}$${\estilo de visualización A}$$${\displaystyle Q={\frac {kA}{\mu L}}\Delta p}$$

Tenga en cuenta que la relación:

$${\displaystyle R={\frac {\mu L}{kA}}}$$

se puede definir como la resistencia hidráulica de la ley de Darcy .

La ley de Darcy se puede generalizar a una forma local:

donde es el gradiente hidráulico y es el flujo volumétrico que aquí también se denomina velocidad superficial . Nótese que la relación:${\displaystyle \nabla p}$${\displaystyle \mathbf {q}}$

$${\displaystyle \sigma ={\frac {k}{\mu }}}$$

Puede considerarse como la conductividad hidráulica de la ley de Darcy .

En la forma integral (menos general), el flujo volumétrico y el gradiente de presión corresponden a las relaciones:

${\displaystyle q={\frac {Q}{A}}}$

${\displaystyle \nabla p={\frac {\Delta p}{L}}}$.

En el caso de un medio poroso anisotrópico, la permeabilidad es un tensor de segundo orden , y en notación tensorial se puede escribir la ley más general:

Tenga en cuenta que la cantidad , a menudo denominada flujo de Darcy o velocidad de Darcy, no es la velocidad a la que el fluido viaja a través de los poros. La velocidad de flujo ( u ) está relacionada con el flujo ( q ) por la porosidad ( φ ) con la siguiente ecuación:${\displaystyle \mathbf {q}}$

${\displaystyle \mathbf {q} =\varphi \,\mathbf {u} .}$

La ecuación constitutiva de Darcy, para el flujo monofásico (fluido), es la ecuación que define la permeabilidad absoluta (permeabilidad monofásica).

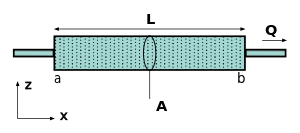
Con referencia al diagrama de la derecha, la velocidad de flujo está en unidades SI , y dado que la porosidad φ es un número adimensional , el flujo de Darcy , o descarga por unidad de área, también se define en unidades ; la permeabilidad en unidades , la viscosidad dinámica en unidades y el gradiente hidráulico está en unidades . ${\displaystyle \mathrm {(m/s)} }$${\displaystyle \mathbf {q}}$${\displaystyle \mathrm {(m/s)} }$${\estilo de visualización k}$${\displaystyle \mathrm {(m^{2})} }$ ${\estilo de visualización \mu}$${\displaystyle \mathrm {(Pa\cdot s)} }$${\displaystyle \mathrm {(Pa/m)} }$

En la forma integral, la caída de presión total está en unidades , y es la longitud de la muestra en unidades , el caudal volumétrico de Darcy , o descarga, también se define en unidades y el área de la sección transversal en unidades . Varios de estos parámetros se utilizan en definiciones alternativas a continuación. Se utiliza un signo negativo en la definición del flujo siguiendo la convención de física estándar de que los fluidos fluyen desde regiones de alta presión a regiones de baja presión. Tenga en cuenta que la altura de elevación debe tenerse en cuenta si la entrada y la salida están a diferentes elevaciones. Si el cambio de presión es negativo, entonces el flujo será en la dirección x positiva . Ha habido varias propuestas para una ecuación constitutiva para la permeabilidad absoluta, y la más famosa es probablemente la ecuación de Kozeny (también llamada ecuación de Kozeny-Carman ).${\displaystyle \Delta p=p_{b}-p_{a}}$${\displaystyle \mathrm {(Pa)} }$${\estilo de visualización L}$${\displaystyle \mathrm {(m)} }$${\estilo de visualización Q}$${\displaystyle \mathrm {(m^{3}/s)} }$${\estilo de visualización A}$${\displaystyle \mathrm {(m^{2})} }$

Considerando la relación de presión de fluido estático ( ley de Stevin ):

$${\displaystyle p=\rho gh}$$También se puede declinar la forma integral en la ecuación: donde ν es la viscosidad cinemática . La conductividad hidráulica correspondiente es, por tanto:$${\displaystyle Q={\frac {kAg}{\nu L}}\,{\Delta h}}$$

${\displaystyle K={\frac {k\rho g}{\mu }}={\frac {kg}{\nu }}.}$

La ley de Darcy es un enunciado matemático simple que resume claramente varias propiedades familiares que exhibe el agua subterránea que fluye en los acuíferos , entre ellas:

• Si no hay gradiente de presión a lo largo de una distancia, no se produce flujo (estas son condiciones hidrostáticas ),
• Si hay un gradiente de presión, el flujo ocurrirá desde alta presión hacia baja presión (opuesta a la dirección del gradiente creciente; de ​​ahí el signo negativo en la ley de Darcy),
• Cuanto mayor sea el gradiente de presión (a través del mismo material de formación), mayor será la tasa de descarga y
• La velocidad de descarga del fluido a menudo será diferente —a través de diferentes materiales de formación (o incluso a través del mismo material, en una dirección diferente)— incluso si existe el mismo gradiente de presión en ambos casos.

Una ilustración gráfica del uso de la ecuación de flujo de agua subterránea en estado estable (basada en la ley de Darcy y la conservación de la masa) es la construcción de redes de flujo , para cuantificar la cantidad de agua subterránea que fluye bajo una presa .

La ley de Darcy sólo es válida para flujos lentos y viscosos ; sin embargo, la mayoría de los casos de flujo de agua subterránea caen en esta categoría. Normalmente, cualquier flujo con un número de Reynolds inferior a uno es claramente laminar, y sería válido aplicar la ley de Darcy. Las pruebas experimentales han demostrado que los regímenes de flujo con números de Reynolds de hasta 10 pueden seguir siendo darcianos, como en el caso del flujo de agua subterránea. El número de Reynolds (un parámetro adimensional) para el flujo en medios porosos se expresa normalmente como

${\displaystyle \mathrm {Re} ={\frac {qd}{\nu }}\,,}$

donde ν es la viscosidad cinemática del agua , q es la descarga específica (no la velocidad de poro — con unidades de longitud por tiempo), d es un diámetro de grano representativo para el medio poroso (la opción estándar es math| d ₃₀ , que es el tamaño de paso del 30% de un análisis de tamaño de grano utilizando tamices — con unidades de longitud).

Para flujo estacionario, progresivo e incompresible, es decirD ( ρu _i )/Dt⁠ ≈ 0 , la ecuación de Navier–Stokes se simplifica a la ecuación de Stokes , que al descuidar el término global es:

${\displaystyle \mu \nabla ^{2}u_{i}-\partial _{i}p=0\,,}$

donde μ es la viscosidad, u _i es la velocidad en la dirección i y p es la presión. Suponiendo que la fuerza de resistencia viscosa es lineal con la velocidad, podemos escribir:

${\displaystyle -\left(k^{-1}\right)_{ij}\mu \varphi u_{j}-\partial _{i}p=0\,,}$

donde φ es la porosidad y k _ij es el tensor de permeabilidad de segundo orden. Esto da la velocidad en la dirección n ,

${\displaystyle k_{ni}\left(k^{-1}\right)_{ij}u_{j}=\delta _{nj}u_{j}=u_{n}=-{\frac {k_ {ni}}{\varphi \mu }}\partial _ {i}p\,,}$

que da la ley de Darcy para la densidad de flujo volumétrico en la dirección n ,

${\displaystyle q_{n}=-{\frac {k_{ni}}{\mu }}\,\partial _{i}p\,.}$

En medios porosos isótropos, los elementos fuera de la diagonal en el tensor de permeabilidad son cero, k _ij = 0 para i ≠ j y los elementos diagonales son idénticos, k _ii = k , y la forma común se obtiene como se muestra a continuación, lo que permite la determinación de la velocidad del flujo de líquido resolviendo un conjunto de ecuaciones en una región dada. ^[5]

${\displaystyle {\boldsymbol {q}}=-{\frac {k}{\mu }}\,{\boldsymbol {\nabla }}p\,.}$

La ecuación anterior es una ecuación rectora para el flujo de fluido monofásico en un medio poroso.

Otra derivación de la ley de Darcy se utiliza ampliamente en la ingeniería petrolera para determinar el flujo a través de medios permeables; la más simple de ellas es para una formación rocosa homogénea unidimensional con una sola fase de fluido y una viscosidad de fluido constante .

Casi todos los yacimientos de petróleo tienen una zona de agua por debajo de la zona de petróleo, y algunos también tienen una capa de gas por encima de la zona de petróleo. Cuando la presión del yacimiento cae debido a la producción de petróleo, el agua fluye hacia la zona de petróleo desde abajo, y el gas fluye hacia la zona de petróleo desde arriba (si existe la capa de gas), y obtenemos un flujo simultáneo y una mezcla inmiscible de todas las fases de fluido en la zona de petróleo. El operador del campo petrolero también puede inyectar agua (y/o gas) para mejorar la producción de petróleo. Por lo tanto, la industria petrolera está utilizando una ecuación de Darcy generalizada para el flujo multifásico que fue desarrollada por Muskat et alios. Debido a que el nombre de Darcy está tan extendido y fuertemente asociado con el flujo en medios porosos, la ecuación multifásica se denota ley de Darcy para flujo multifásico o ecuación (o ley) de Darcy generalizada o simplemente ecuación (o ley) de Darcy o simplemente ecuación de flujo si el contexto dice que el texto está discutiendo la ecuación multifásica de Muskat et alios. El flujo multifásico en yacimientos de petróleo y gas es un tema amplio, y uno de los muchos artículos sobre este tema es la ley de Darcy para el flujo multifásico .

Varios artículos han utilizado la ley de Darcy para modelar la física de la preparación en una cafetera moka , específicamente cómo el agua caliente se filtra a través de los granos de café bajo presión, comenzando con un artículo de 2001 de Varlamov y Balestrino, ^[6] y continuando con un artículo de 2007 de Gianino, ^[7] un artículo de 2008 de Navarini et al., ^[8] y un artículo de 2008 de W. King. ^[9] Los artículos tomarán la permeabilidad del café como constante como una simplificación o medirán el cambio a través del proceso de preparación.

La ley de Darcy se puede expresar de manera muy general como:

${\displaystyle \mathbf {q} =-K\nabla h}$

donde q es el vector de flujo de volumen del fluido en un punto particular del medio, h es la carga hidráulica total y K es el tensor de conductividad hidráulica en ese punto. La conductividad hidráulica a menudo se puede aproximar como un escalar . (Obsérvese la analogía con la ley de Ohm en electrostática. El vector de flujo es análogo a la densidad de corriente, la carga es análoga al voltaje y la conductividad hidráulica es análoga a la conductividad eléctrica).

En el caso de flujos en medios porosos con números de Reynolds superiores a aproximadamente 1 a 10, los efectos inerciales también pueden resultar significativos. A veces se añade un término inercial a la ecuación de Darcy, conocido como término de Forchheimer . Este término puede explicar el comportamiento no lineal de la diferencia de presión frente a los datos de flujo. ^[10]

${\displaystyle \nabla p=-{\frac {\mu }{k}}q-{\frac {\rho }{k_{1}}}q^{2}\,,}$

donde el término adicional k ₁ se conoce como permeabilidad inercial, en unidades de longitud .${\displaystyle \mathrm {(m)} }$

El flujo en el medio de un yacimiento de arenisca es tan lento que normalmente no se necesita la ecuación de Forchheimer, pero el flujo de gas hacia un pozo de producción de gas puede ser lo suficientemente alto como para justificar su uso. En este caso, los cálculos del rendimiento de entrada para el pozo, no la celda de la cuadrícula del modelo 3D, se basan en la ecuación de Forchheimer. El efecto de esto es que aparece una capa adicional dependiente de la velocidad en la fórmula de rendimiento de entrada.

Algunos yacimientos carbonatados tienen muchas fracturas, y la ecuación de Darcy para el flujo multifásico se generaliza para regular tanto el flujo en las fracturas como el flujo en la matriz (es decir, la roca porosa tradicional). La superficie irregular de las paredes de las fracturas y el alto caudal en las fracturas pueden justificar el uso de la ecuación de Forchheimer.

Para flujos de gas en pequeñas dimensiones características (por ejemplo, arena muy fina, estructuras nanoporosas, etc.), las interacciones entre partículas y paredes se vuelven más frecuentes, lo que da lugar a una fricción adicional en la pared (fricción de Knudsen). Para un flujo en esta región, donde están presentes tanto la fricción viscosa como la de Knudsen , se necesita utilizar una nueva formulación. Knudsen presentó un modelo semiempírico para el flujo en régimen de transición basado en sus experimentos en pequeños capilares. ^{[11] [12]} Para un medio poroso, la ecuación de Knudsen puede expresarse como ^[12]

${\displaystyle N=-\left({\frac {k}{\mu }}{\frac {p_{a}+p_{b}}{2}}+D_{\mathrm {K} }^{\mathrm {eff} }\right){\frac {1}{R_{\mathrm {g} }T}}{\frac {p_{\mathrm {b} }-p_{\mathrm {a} }}{L}}\,,}$

donde N es el flujo molar, R _g es la constante del gas, T es la temperatura, D^{Efectivamente}
_Kes la difusividad de Knudsen efectiva del medio poroso. El modelo también se puede derivar del modelo de fricción binaria basado en el primer principio (BFM). ^{[13] [14]} La ecuación diferencial del flujo de transición en medios porosos basada en BFM se da como ^[13]

${\displaystyle {\frac {\partial p}{\partial x}}=-R_{\mathrm {g} }T\left({\frac {kp}{\mu }}+D_{\mathrm {K} }\right)^{-1}N\,.}$

Esta ecuación es válida tanto para capilares como para medios porosos. La terminología del efecto Knudsen y la difusividad de Knudsen es más común en ingeniería mecánica y química . En ingeniería geológica y petroquímica, este efecto se conoce como efecto Klinkenberg . Utilizando la definición de flujo molar, la ecuación anterior se puede reescribir como

${\displaystyle {\frac {\partial p}{\partial x}}=-R_{\mathrm {g} }T\left({\frac {kp}{\mu }}+D_{\mathrm {K} }\right)^{-1}{\dfrac {p}{R_{\mathrm {g} }T}}q\,.}$

Esta ecuación se puede reorganizar en la siguiente ecuación

${\displaystyle q=-{\frac {k}{\mu }}\left(1+{\frac {D_{\mathrm {K} }\mu }{k}}{\frac {1}{p}}\right){\frac {\partial p}{\partial x}}\,.}$

Comparando esta ecuación con la ley de Darcy convencional, se puede dar una nueva formulación como

${\displaystyle q=-{\frac {k^{\mathrm {eff} }}{\mu }}{\frac {\partial p}{\partial x}}\,,}$

dónde

${\displaystyle k^{\mathrm {eff} }=k\left(1+{\frac {D_{\mathrm {K} }\mu }{k}}{\frac {1}{p}}\right)\,.}$

Esto es equivalente a la formulación de permeabilidad efectiva propuesta por Klinkenberg: ^[15]

${\displaystyle k^{\mathrm {eff} }=k\left(1+{\frac {b}{p}}\right)\,.}$

donde b se conoce como el parámetro de Klinkenberg, que depende de la estructura del gas y del medio poroso. Esto es bastante evidente si comparamos las formulaciones anteriores. El parámetro de Klinkenberg b depende de la permeabilidad, la difusividad de Knudsen y la viscosidad (es decir, tanto de las propiedades del gas como del medio poroso).

Para escalas de tiempo muy cortas, se puede agregar una derivada temporal del flujo a la ley de Darcy, lo que da como resultado soluciones válidas en tiempos muy pequeños (en transferencia de calor, esto se llama la forma modificada de la ley de Fourier ).

${\displaystyle \tau {\frac {\partial q}{\partial t}}+q=-k\nabla h\,,}$

donde τ es una constante de tiempo muy pequeña que hace que esta ecuación se reduzca a la forma normal de la ley de Darcy en tiempos "normales" (> nanosegundos ). La razón principal para hacer esto es que la ecuación de flujo de agua subterránea regular ( ecuación de difusión ) conduce a singularidades en límites de carga constante en tiempos muy pequeños. Esta forma es matemáticamente más rigurosa pero conduce a una ecuación de flujo de agua subterránea hiperbólica , que es más difícil de resolver y solo es útil en tiempos muy pequeños, típicamente fuera del ámbito del uso práctico.

Otra extensión de la forma tradicional de la ley de Darcy es el término de Brinkman, que se utiliza para explicar el flujo transicional entre límites (introducido por Brinkman en 1949 ^[16] ),

${\displaystyle -\beta \nabla ^{2}q+q=-{\frac {k}{\mu }}\nabla p\,,}$

donde β es un término de viscosidad efectiva . Este término de corrección tiene en cuenta el flujo a través del medio donde los granos del medio son porosos, pero es difícil de usar y, por lo general, se descuida.

La ley de Darcy es válida para el flujo laminar a través de sedimentos . En sedimentos de grano fino, las dimensiones de los intersticios son pequeñas; por lo tanto, el flujo es laminar. Los sedimentos de grano grueso también se comportan de manera similar, pero en sedimentos de grano muy grueso, el flujo puede ser turbulento . ^[17] Por lo tanto, la ley de Darcy no siempre es válida en tales sedimentos. Para el flujo a través de tuberías circulares comerciales, el flujo es laminar cuando el número de Reynolds es menor que 2000 y turbulento cuando es mayor que 4000, pero en algunos sedimentos, se ha encontrado que el flujo es laminar cuando el valor del número de Reynolds es menor que 1. ^[18]

• El darcy , una unidad de permeabilidad de fluidos
• Hidrogeología
• Ecuación del flujo de agua subterránea
• Modelo matemático
• Ecuaciones del petróleo negro
• Ley de Fick
• Ecuación de Ergun