Ley de Rayleigh-Jeans

En física , la ley de Rayleigh-Jeans es una aproximación a la radiancia espectral de la radiación electromagnética en función de la longitud de onda de un cuerpo negro a una temperatura dada mediante argumentos clásicos. Para la longitud de onda λ , es donde es la radiancia espectral (la potencia emitida por unidad de área de emisión, por estereorradián , por unidad de longitud de onda), es la velocidad de la luz , es la constante de Boltzmann y es la temperatura en kelvin . Para la frecuencia , la expresión es en cambio$${\displaystyle B_{\lambda }(T)={\frac {2ck_{\text{B}}T}{\lambda ^{4}}},}$$${\displaystyle B_{\lambda}}$${\estilo de visualización c}$${\displaystyle k_{\text{B}}}$${\estilo de visualización T}$ ${\estilo de visualización \nu}$$${\displaystyle B_{\nu }(T)={\frac {2\nu ^{2}k_{\text{B}}T}{c^{2}}}.}$$

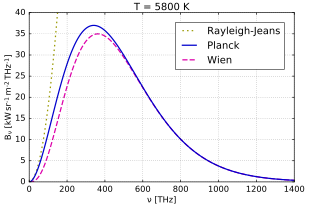
La ley de Rayleigh-Jeans concuerda con los resultados experimentales en longitudes de onda grandes (frecuencias bajas), pero discrepa fuertemente en longitudes de onda cortas (frecuencias altas). Esta inconsistencia entre las observaciones y las predicciones de la física clásica se conoce comúnmente como la catástrofe ultravioleta . ^{[1] [2]} La ley de Planck , que proporciona la radiación correcta en todas las frecuencias, tiene la ley de Rayleigh-Jeans como su límite de baja frecuencia.

En 1900, el físico británico Lord Rayleigh derivó la dependencia λ ^{−4 de la ley de Rayleigh-Jeans basándose en argumentos físicos clásicos, apoyándose en el} teorema de equipartición . Esta ley predijo una salida de energía que diverge hacia el infinito a medida que la longitud de onda se acerca a cero (ya que la frecuencia tiende al infinito). Las mediciones de la emisión espectral de cuerpos negros reales revelaron que la emisión concordaba con el cálculo de Rayleigh a bajas frecuencias, pero divergía a altas frecuencias, alcanzando un máximo y luego cayendo con la frecuencia, por lo que la energía total emitida es finita. Rayleigh reconoció el comportamiento no físico de su fórmula a altas frecuencias e introdujo un límite ad hoc para corregirlo, pero los experimentalistas descubrieron que su límite no concordaba con los datos. ^{[1] [3]} Hendrik Lorentz también presentó una derivación de la dependencia de la longitud de onda en 1903. Derivaciones más completas, que incluían la constante de proporcionalidad, fueron presentadas en 1905 por Rayleigh y Sir James Jeans e independientemente por Albert Einstein . ^[3] Rayleigh creía que esta discrepancia podía resolverse si el teorema de equipartición no era válido para vibraciones de alta frecuencia, mientras que Jeans argumentaba que la causa subyacente era que la materia y el éter luminífero no estaban en equilibrio térmico. ^[3]

Rayleigh publicó su primera derivación de la dependencia de la frecuencia en junio de 1900. Planck descubrió la curva que ahora se conoce como ley de Planck en octubre de ese año y la presentó en diciembre. ^[3] La intención original de Planck era encontrar una derivación satisfactoria de la expresión de Wien para la curva de radiación del cuerpo negro, que describiera con precisión los datos a altas frecuencias. Planck encontró que la derivación original de Wien era inadecuada e ideó la suya propia. Luego, después de enterarse de que los resultados experimentales más recientes no coincidían con sus predicciones para las frecuencias bajas, Planck revisó su cálculo y obtuvo lo que ahora se llama ley de Planck. ^[4]

En 1900, Max Planck obtuvo empíricamente una expresión para la radiación del cuerpo negro expresada en términos de longitud de onda λ = c / ν ( ley de Planck ): donde h es la constante de Planck y k _B es la constante de Boltzmann . La ley de Planck no sufre una catástrofe ultravioleta y concuerda bien con los datos experimentales, pero su significado completo (que finalmente condujo a la teoría cuántica) solo se apreció varios años después. Desde entonces, en el límite de altas temperaturas o longitudes de onda largas, el término en la exponencial se vuelve pequeño y la exponencial se aproxima bien con el término de primer orden del polinomio de Taylor :$${\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\text{B}}T}}-1}},}$$$${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots ,}$$$${\displaystyle e^{\frac {hc}{\lambda k_{\text{B}}T}}\aprox 1+{\frac {hc}{\lambda k_{\text{B}}T}}.}$$

Entonces$${\displaystyle {\frac {1}{e^{\frac {hc}{\lambda k_{\text{B}}T}}-1}}\approx {\frac {1}{\frac {hc}{\lambda k_{\text{B}}T}}}={\frac {\lambda k_{\text{B}}T}{hc}}.}$$

Esto da como resultado que la fórmula del cuerpo negro de Planck se reduzca a, que es idéntica a la expresión de Rayleigh-Jeans derivada clásicamente.$${\displaystyle B_{\lambda }(T)={\frac {2ck_{\text{B}}T}{\lambda ^{4}}},}$$

El mismo argumento se puede aplicar a la radiación del cuerpo negro expresada en términos de frecuencia ν = c / λ . En el límite de frecuencias pequeñas, es decir ,${\displaystyle h\nu \ll k_{\text{B}}T}$$${\displaystyle B_{\nu}(T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{k_{\text{B}}T}}-1}}\approx {\frac {2h\nu ^{3}}{c^{2}}}\cdot {\frac {k_{\text{B}}T}{h\nu }}={\frac {2\nu ^{2}k_{\mathrm {B} }T}{c^{2}}}.}$$

Esta última expresión es la ley de Rayleigh-Jeans en el límite de frecuencias pequeñas.

Al comparar las expresiones dependientes de la frecuencia y la longitud de onda de la ley de Rayleigh-Jeans, es importante recordar que y Nótese que estas dos expresiones tienen unidades diferentes, ya que un paso en la longitud de onda no es equivalente a un paso en la frecuencia. Por lo tanto, incluso después de sustituir el valor , porque tiene unidades de energía emitida por unidad de tiempo por unidad de área de superficie emisora, por unidad de ángulo sólido, por unidad de longitud de onda , mientras que tiene unidades de energía emitida por unidad de tiempo por unidad de área de superficie emisora, por unidad de ángulo sólido, por unidad de frecuencia . Para ser consistentes, debemos usar la igualdad donde ambos lados ahora tienen unidades de potencia (energía emitida por unidad de tiempo) por unidad de área de superficie emisora, por unidad de ángulo sólido.$${\displaystyle {\frac {dP}{d\lambda}}=B_{\lambda}(T)}$$$${\displaystyle {\frac {dP}{d\nu }}=B_{\nu }(T).}$$${\estilo de visualización d\lambda}$${\estilo de visualización d\nu}$$${\displaystyle B_{\lambda}(T)\neq B_{\nu}(T),}$$${\displaystyle \lambda =c/\nu }$$Estilo de visualización B_{\lambda}(T)}$${\displaystyle B_{\nu}(T)}$$${\displaystyle B_{\lambda }\,d\lambda =dP=B_{\nu }\,d\nu ,}$$

Comenzando con la ley de Rayleigh-Jeans en términos de longitud de onda, llegamos a donde Esto conduce a$${\displaystyle B_{\lambda }(T)=B_{\nu }(T){\frac {d\nu }{d\lambda }},}$$$${\displaystyle {\frac {d\nu }{d\lambda }}={\frac {d}{d\lambda }}\left({\frac {c}{\lambda }}\right)=-{\frac {c}{\lambda ^{2}}}.}$$$${\displaystyle B_{\lambda }(T)={\frac {2k_{\text{B}}T\left({\frac {c}{\lambda }}\right)^{2}}{c^{2}}}\times {\frac {c}{\lambda ^{2}}}={\frac {2ck_{\text{B}}T}{\lambda ^{4}}}.}$$

Dependiendo de la aplicación, la función de Planck se puede expresar de tres formas diferentes. La primera implica la energía emitida por unidad de tiempo por unidad de área de superficie emisora, por unidad de ángulo sólido, por unidad espectral. En esta forma, la función de Planck y los límites de Rayleigh-Jeans asociados se dan por o$${\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\text{B}}T}}-1}}\approx {\frac {2ck_{\text{B}}T}{\lambda ^{4}}}}$$$${\displaystyle B_{\nu }(T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{k_{\text{B}}T}}-1}}\approx {\frac {2k_{\text{B}}T\nu ^{2}}{c^{2}}}.}$$

Alternativamente, la ley de Planck puede escribirse como una expresión para la potencia emitida integrada sobre todos los ángulos sólidos. En esta forma, la función de Planck y los límites de Rayleigh-Jeans asociados se dan por o${\displaystyle I(\nu ,T)=\pi B_{\nu }(T)}$$${\displaystyle I(\lambda ,T)={\frac {2\pi hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\text{B}}T}}-1}}\approx {\frac {2\pi ck_{\text{B}}T}{\lambda ^{4}}}}$$$${\displaystyle I(\nu ,T)={\frac {2\pi h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{k_{\text{B}}T}}-1}}\approx {\frac {2\pi k_{\text{B}}T\nu ^{2}}{c^{2}}}.}$$

En otros casos, la ley de Planck se escribe como energía por unidad de volumen (densidad de energía). En esta forma, la función de Planck y los límites de Rayleigh-Jeans asociados se dan por o${\textstyle u(\nu ,T)={\frac {4\pi }{c}}B_{\nu }(T)}$$${\displaystyle u(\lambda ,T)={\frac {8\pi hc}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\text{B}}T}}-1}}\approx {\frac {8\pi k_{\text{B}}T}{\lambda ^{4}}}}$$$${\displaystyle u(\nu ,T)={\frac {8\pi h\nu ^{3}}{c^{3}}}{\frac {1}{e^{\frac {h\nu }{k_{\text{B}}T}}-1}}\approx {\frac {8\pi k_{\text{B}}T\nu ^{2}}{c^{3}}}.}$$

• Ley de Stefan-Boltzmann
• Ley de desplazamiento de Wien
• Aproximación de Viena
• Ecuación de Sakuma-Hattori

• Derivación de la ley de Rayleigh-Jeans
• Derivación de los modos de una onda en un cubo