Ritmo (acústica)

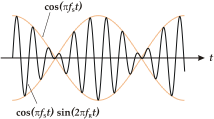
En acústica , un pulso es un patrón de interferencia entre dos sonidos de frecuencias ligeramente diferentes , percibido como una variación periódica en el volumen cuya tasa es la diferencia de las dos frecuencias.

Con instrumentos de afinación que pueden producir tonos sostenidos, los pulsos se pueden reconocer fácilmente. Afinar dos tonos al unísono presentará un efecto peculiar: cuando los dos tonos son cercanos en tono pero no idénticos, la diferencia en frecuencia genera el pulso. El volumen varía como en un trémolo a medida que los sonidos interfieren alternativamente de manera constructiva y destructiva. A medida que los dos tonos se acercan gradualmente al unísono, el pulso se hace más lento y puede volverse tan lento que sea imperceptible. A medida que los dos tonos se alejan más, su frecuencia de pulso comienza a acercarse al rango de percepción del tono humano ^[1] , el pulso comienza a sonar como una nota y se produce un tono combinado .

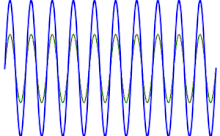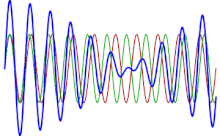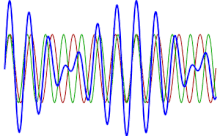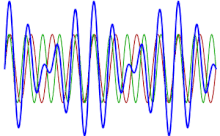
Este fenómeno es más conocido en acústica o música, aunque puede encontrarse en cualquier sistema lineal:

"Según la ley de superposición , dos tonos que suenan simultáneamente se superponen de una manera muy sencilla: se suman sus amplitudes". ^[2]

Si se dibuja un gráfico para mostrar la función correspondiente al sonido total de dos cuerdas , se puede ver que los máximos y mínimos ya no son constantes (como cuando se toca una nota pura), sino que cambian con el tiempo: cuando las dos ondas están desfasadas casi 180 grados , los máximos de una onda cancelan los mínimos de la otra, mientras que cuando están casi en fase, sus máximos se suman, aumentando el volumen percibido.

Se puede demostrar (con la ayuda de una identidad trigonométrica de suma-producto ) que la suma de dos ondas sinusoidales de amplitud unitaria se puede expresar como una onda portadora de frecuencia ⁠f1 + f2_​​/2⁠ cuya amplitud está modulada por una onda envolvente de frecuencia ⁠F1 - F2_​​/2⁠ : ^[3]

${\displaystyle \cos(2\pi f_{1}t)+\cos(2\pi f_{2}t)}={2\;\underbrace {\cos \left(2\pi {\frac {f_{1}+f_{2}}{2}}t\right)} _{\text{portadora}}\;\underbrace {\cos \left(2\pi {\frac {f_{1}-f_{2}}{2}}t\right)} _{\text{envolvente}}}$

Como cada ráfaga del patrón de modulación está invertida, cada pico se reemplaza por un valle y viceversa. Se percibe que la envolvente tiene el doble de frecuencia que el coseno modulador, lo que significa que la frecuencia de batido audible (si está en el rango audible) es: ^[4]

${\displaystyle f_{\text{ritmo}}=f_{1}-f_{2}\,.}$

Un ritmo binaural es una ilusión auditiva que se percibe cuando dos ondas sinusoidales de tono puro diferentes , con una diferencia entre ellas de aproximadamente 40 Hz, se presentan a un oyente de forma dicótica (una a través de cada oído ).

Por ejemplo, si se presenta un tono puro de 530 Hz al oído derecho de un sujeto, mientras que se presenta un tono puro de 520 Hz al oído izquierdo del sujeto, el oyente oirá un latido a una frecuencia de 10 Hz, tal como si los dos tonos se presentaran monoauralmente, pero el latido también tendrá un elemento de movimiento lateral.

La percepción del ritmo binaural se origina en el colículo inferior del mesencéfalo y el complejo olivar superior del tronco encefálico , donde las señales auditivas de cada oído se integran y precipitan impulsos eléctricos a lo largo de vías neuronales a través de la formación reticular hasta el mesencéfalo hasta el tálamo , la corteza auditiva y otras regiones corticales. ^[5]

Según una revisión sistemática de 2023, los estudios han investigado algunos de los supuestos efectos positivos en las áreas de procesamiento cognitivo, estados afectivos (como la ansiedad), estado de ánimo, percepción del dolor, meditación y relajación, divagación mental y creatividad, pero las técnicas no eran comparables y los resultados no fueron concluyentes. De los catorce estudios revisados, cinco informaron resultados en línea con la hipótesis del arrastre de ondas cerebrales , ocho estudios informaron resultados contradictorios y uno tuvo resultados mixtos. Los autores recomiendan la estandarización de los enfoques de estudio para estudios futuros para que los resultados puedan compararse de manera más efectiva. ^[6]

Los músicos suelen utilizar los pulsos de interferencia de forma objetiva para comprobar la afinación al unísono , la quinta perfecta u otros intervalos armónicos simples. ^[7] Los afinadores de piano y órgano utilizan un método que implica contar los pulsos, apuntando a un número particular para un intervalo específico.

El compositor Alvin Lucier ha escrito muchas piezas que presentan pulsos de interferencia como su foco principal. El compositor italiano Giacinto Scelsi , cuyo estilo se basa en oscilaciones microtonales de unísonos, exploró ampliamente los efectos texturales de los pulsos de interferencia, particularmente en sus últimas obras como los solos de violín Xnoybis (1964) y L'âme ailée / L'âme ouverte (1973), que los presentan de forma destacada (Scelsi trató y anotó cada cuerda del instrumento como una parte separada, de modo que sus solos de violín son efectivamente cuartetos de una cuerda, donde diferentes cuerdas del violín pueden tocar simultáneamente la misma nota con cambios microtonales, de modo que se generan los patrones de interferencia). La música del compositor Phill Niblock se basa completamente en pulsos causados ​​por diferencias microtonales. ^[8] El ingeniero informático Toso Pankovski inventó un método basado en la interferencia auditiva para filtrar a los participantes en estudios auditivos en línea en función de los auriculares y el contexto dicótico (si los canales estéreo están mezclados o completamente separados). ^[9]

Los radioaficionados utilizan los términos "cero-batido" o "cero-beat" para sintonizar con precisión una frecuencia de onda portadora deseada reduciendo manualmente el número de pulsos de interferencia, ^[10] fundamentalmente el mismo proceso de sintonización utilizado por los músicos.

Formas de onda palpitantes (alta frecuencia)

220 Hz A ₃ (canal izquierdo) y 207,65 Hz G ♯ ₃ (canal derecho) latiendo a 12,35 Hz

---

¿Tiene problemas para reproducir este archivo? Consulte la ayuda multimedia .

Formas de onda palpitantes (baja frecuencia)

_{Tono A 3} de 220 Hz y 222 Hz que late a 2 Hz

---

¿Tiene problemas para reproducir este archivo? Consulte la ayuda multimedia .

• Respuesta sensorial meridiana autónoma (ASMR)
• Consonancia y disonancia
• Afinación de gamelan
• Heterodino
• Patrón muaré , una forma de interferencia espacial que genera nuevas frecuencias.
• Música y sueño
• Voz celeste

• Thaut, Michael H. (2005). Ritmo, música y cerebro: fundamentos científicos y aplicaciones clínicas (1.ª edición en rústica). Nueva York: Routledge. ISBN 978-0415973700.
• Berger, Jonathan; Turow, Gabe, eds. (2011). Música, ciencia y el cerebro rítmico: implicaciones culturales y clínicas . Routledge. ISBN 978-0415890595.

• Materiales de aprendizaje relacionados con Beat (acústica) en Wikiversidad
• Subprograma Javascript, MIT
• Animaciones acústicas y vibratorias, DA Russell, Universidad Estatal de Pensilvania
• Una aplicación Java que muestra la formación de ritmos debido a la interferencia de dos ondas de frecuencias ligeramente diferentes.
• Curvas de Lissajous: Simulación interactiva de representaciones gráficas de intervalos musicales, ritmos, interferencias y cuerdas vibrantes.
• Las conferencias de física de Feynman, vol. I, cap. 48: Ritmos