Lenguaje formal

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Lenguaje formal» – noticias  · periódicos  · libros  · académico  · JSTOR ( marzo de 2024 ) ( Aprenda cómo y cuándo eliminar este mensaje )

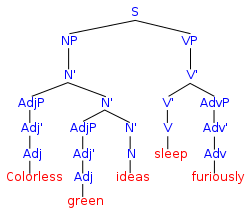
En lógica , matemáticas , informática y lingüística , un lenguaje formal consiste en palabras cuyas letras se toman de un alfabeto y están bien formadas de acuerdo con un conjunto específico de reglas llamadas gramática formal .

El alfabeto de un lenguaje formal consiste en símbolos, letras o tokens que se concatenan en cadenas llamadas palabras. ^[1] Las palabras que pertenecen a un lenguaje formal en particular a veces se denominan palabras bien formadas o fórmulas bien formadas . Un lenguaje formal a menudo se define por medio de una gramática formal como una gramática regular o una gramática libre de contexto , que consiste en sus reglas de formación .

En informática, los lenguajes formales se utilizan, entre otros, como base para definir la gramática de los lenguajes de programación y versiones formalizadas de subconjuntos de lenguajes naturales, en los que las palabras del lenguaje representan conceptos que están asociados a significados o semántica . En la teoría de la complejidad computacional , los problemas de decisión se definen típicamente como lenguajes formales, y las clases de complejidad se definen como los conjuntos de los lenguajes formales que pueden ser analizados por máquinas con un poder computacional limitado. En lógica y los fundamentos de las matemáticas , los lenguajes formales se utilizan para representar la sintaxis de los sistemas axiomáticos , y el formalismo matemático es la filosofía de que todas las matemáticas pueden reducirse a la manipulación sintáctica de los lenguajes formales de esta manera.

El campo de la teoría formal del lenguaje estudia principalmente los aspectos puramente sintácticos de dichos lenguajes, es decir, sus patrones estructurales internos. La teoría formal del lenguaje surgió de la lingüística como una forma de entender las regularidades sintácticas de los lenguajes naturales .

Esta sección necesita ser ampliada . Puedes ayudar agregándole algo. ( Marzo de 2021 )

En el siglo XVII, Gottfried Leibniz imaginó y describió la characterisa universalis , un lenguaje universal y formal que utilizaba pictogramas . Más tarde, Carl Friedrich Gauss investigó el problema de los códigos de Gauss . ^[2]

Gottlob Frege intentó hacer realidad las ideas de Leibniz mediante un sistema de notación esbozado por primera vez en Begriffsschrift (1879) y desarrollado más plenamente en su Grundgesetze der Arithmetik (1893/1903) en dos volúmenes. ^[3] En él se describía un "lenguaje formal del lenguaje puro". ^[4]

En la primera mitad del siglo XX se produjeron varios avances relacionados con los lenguajes formales. Axel Thue publicó cuatro artículos relacionados con las palabras y el lenguaje entre 1906 y 1914. El último de ellos introdujo lo que Emil Post más tarde denominó "sistemas de Thue" y dio un ejemplo temprano de un problema indecidible . ^[5] Post utilizaría más tarde este artículo como base para una prueba de 1947 "de que el problema de las palabras para los semigrupos era recursivamente insoluble", ^[6] y más tarde ideó el sistema canónico para la creación de lenguajes formales.

En 1907, Leonardo Torres Quevedo introdujo en Viena un lenguaje formal para la descripción de dibujos mecánicos (dispositivos mecánicos) . Publicó "Sobre un sistema de notaciones y símbolos destinados a facilitar la descripción de las máquinas". ^[7] Heinz Zemanek lo calificó como un equivalente a un lenguaje de programación para el control numérico de máquinas herramienta. ^[8]

Noam Chomsky ideó una representación abstracta de los lenguajes formales y naturales, conocida como la jerarquía de Chomsky . ^[9] En 1959, John Backus desarrolló la forma Backus-Naur para describir la sintaxis de un lenguaje de programación de alto nivel, siguiendo su trabajo en la creación de FORTRAN . ^[10] Peter Naur fue el secretario/editor del Informe ALGOL60 en el que utilizó la forma Backus–Naur para describir la parte formal de ALGOL60.

Un alfabeto , en el contexto de los lenguajes formales, puede ser cualquier conjunto ; sus elementos se denominan letras . Un alfabeto puede contener un número infinito de elementos; ^{[nota 1]} sin embargo, la mayoría de las definiciones en la teoría del lenguaje formal especifican alfabetos con un número finito de elementos, y muchos resultados se aplican solo a ellos. A menudo tiene sentido utilizar un alfabeto en el sentido habitual de la palabra, o más generalmente cualquier codificación de caracteres finitos como ASCII o Unicode .

Una palabra sobre un alfabeto puede ser cualquier secuencia finita (es decir, cadena ) de letras. El conjunto de todas las palabras sobre un alfabeto Σ se denota generalmente por Σ ^* (usando la estrella de Kleene ). La longitud de una palabra es el número de letras de las que está compuesta. Para cualquier alfabeto, solo hay una palabra de longitud 0, la palabra vacía , que a menudo se denota por e, ε, λ o incluso Λ. Por concatenación se pueden combinar dos palabras para formar una nueva palabra, cuya longitud es la suma de las longitudes de las palabras originales. El resultado de concatenar una palabra con la palabra vacía es la palabra original.

En algunas aplicaciones, especialmente en lógica , el alfabeto también se conoce como vocabulario y las palabras se conocen como fórmulas u oraciones ; esto rompe la metáfora de letra/palabra y la reemplaza por una metáfora de palabra/oración.

Un lenguaje formal L sobre un alfabeto Σ es un subconjunto de Σ ^* , es decir, un conjunto de palabras sobre ese alfabeto. A veces, los conjuntos de palabras se agrupan en expresiones, mientras que se pueden formular reglas y restricciones para la creación de "expresiones bien formadas".

En informática y matemáticas, que normalmente no tratan lenguajes naturales , el adjetivo "formal" se omite a menudo por considerarlo redundante.

Aunque la teoría del lenguaje formal suele ocuparse de lenguajes formales que se describen mediante algunas reglas sintácticas, la definición real del concepto de "lenguaje formal" es la anterior: un conjunto (posiblemente infinito) de cadenas de longitud finita compuestas por un alfabeto dado, ni más ni menos. En la práctica, hay muchos lenguajes que se pueden describir mediante reglas, como los lenguajes regulares o los lenguajes libres de contexto . La noción de gramática formal puede estar más cerca del concepto intuitivo de "lenguaje", uno descrito mediante reglas sintácticas. Por un abuso de la definición, a menudo se piensa que un lenguaje formal particular está acompañado de una gramática formal que lo describe.

Las siguientes reglas describen un lenguaje formal  L sobre el alfabeto Σ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, =}:

• Toda cadena no vacía que no contenga "+" o "=" y no comience con "0" está  en L.
• La cadena "0 " está en  L.
• Una cadena que contiene "=" está en  L si y solo si hay exactamente un "=", y separa dos cadenas válidas  de L.
• Una cadena que contiene "+" pero no "=" está en  L si y solo si cada "+ " en la cadena separa dos cadenas válidas de  L.
• No hay ninguna cadena en  L aparte de las implicadas en las reglas anteriores.

Según estas reglas, la cadena "23+4=555" está en  L , pero la cadena "=234=+" no. Este lenguaje formal expresa números naturales , sumas bien formadas e igualdades de sumas bien formadas, pero expresa solo su apariencia ( sintaxis ), no su significado ( semántica ). Por ejemplo, en ninguna parte de estas reglas hay ninguna indicación de que "0" significa el número cero, "+" significa suma, "23+4=555" es falso, etc.

En el caso de los lenguajes finitos, se pueden enumerar explícitamente todas las palabras bien formadas. Por ejemplo, podemos describir un lenguaje  L simplemente como L  = {a, b, ab, cba}. El caso degenerado de esta construcción es el lenguaje vacío , que no contiene ninguna palabra ( L  =  ∅ ).

Sin embargo, incluso sobre un alfabeto finito (no vacío) como Σ = {a, b} hay un número infinito de palabras de longitud finita que potencialmente pueden expresarse: "a", "abb", "ababba", "aaababbbbaab", .... Por lo tanto, los lenguajes formales son típicamente infinitos, y describir un lenguaje formal infinito no es tan simple como escribir L  = {a, b, ab, cba}. A continuación se muestran algunos ejemplos de lenguajes formales:

• L = Σ ^* , el conjunto de todas las palabras sobre Σ;
• L = {a} ^* = {a ⁿ }, donde n abarca los números naturales y "a ⁿ " significa "a" repetido n veces (este es el conjunto de palabras que consisten únicamente en el símbolo "a");
• el conjunto de programas sintácticamente correctos en un lenguaje de programación dado (cuya sintaxis suele estar definida por una gramática libre de contexto );
• el conjunto de entradas en las que se detiene una determinada máquina de Turing ; o
• el conjunto de cadenas máximas de caracteres ASCII alfanuméricos en esta línea, es decir, el conjunto {el, conjunto, de, cadenas, máximas, de, caracteres, ASCII, alfanuméricos, en, esta, línea, i, e}.
  

Los lenguajes formales se utilizan como herramientas en múltiples disciplinas. Sin embargo, la teoría del lenguaje formal rara vez se ocupa de lenguajes en particular (excepto como ejemplos), sino que se ocupa principalmente del estudio de varios tipos de formalismos para describir lenguajes. Por ejemplo, un lenguaje puede darse como

• aquellas cadenas generadas por alguna gramática formal ;
• aquellas cadenas descritas o coincidentes con una expresión regular particular ;
• aquellas cadenas aceptadas por algún autómata , como una máquina de Turing o un autómata de estados finitos ;
• aquellas cadenas para las que algún procedimiento de decisión (un algoritmo que formula una secuencia de preguntas relacionadas de SÍ/NO) produce la respuesta SÍ.

Las preguntas típicas que se hacen sobre estos formalismos incluyen:

• ¿Cuál es su poder expresivo? (¿Puede el formalismo X describir todos los idiomas que el formalismo Y puede describir? ¿Puede describir otros idiomas?)
• ¿Cuál es su reconocibilidad? (¿Qué tan difícil es decidir si una palabra dada pertenece a un lenguaje descrito por el formalismo X ?)
• ¿Cuál es su comparabilidad? (¿Qué tan difícil es decidir si dos lenguajes, uno descrito en el formalismo X y otro en el formalismo Y , o en X nuevamente, son en realidad el mismo lenguaje?).

Sorprendentemente, con frecuencia la respuesta a estos problemas de decisión es "no se puede hacer en absoluto" o "es extremadamente caro" (con una caracterización de cuán caro). Por lo tanto, la teoría del lenguaje formal es un área de aplicación importante de la teoría de la computabilidad y la teoría de la complejidad . Los lenguajes formales pueden clasificarse en la jerarquía de Chomsky en función del poder expresivo de su gramática generativa, así como de la complejidad de su autómata de reconocimiento . Las gramáticas libres de contexto y las gramáticas regulares proporcionan un buen compromiso entre expresividad y facilidad de análisis , y se utilizan ampliamente en aplicaciones prácticas.

Ciertas operaciones en los lenguajes son comunes, entre ellas las operaciones de conjuntos estándar, como la unión, la intersección y el complemento. Otra clase de operación es la aplicación de operaciones de cadenas a cada elemento.

Ejemplos: supongamos que y son idiomas que tienen un alfabeto común .$Estilo de visualización L_{1}$$Estilo de visualización L_{2}$${\estilo de visualización \Sigma}$

• La concatenación consta de todas las cadenas de la forma donde es una cadena de y es una cadena de .$Estilo de visualización L_{1}\cdot L_{2}}$${\estilo de visualización vw}$${\estilo de visualización v}$$Estilo de visualización L_{1}$${\estilo de visualización w}$$Estilo de visualización L_{2}$
• La intersección de y consta de todas las cadenas que están contenidas en ambos idiomas.$Estilo de visualización L_{1}\cap L_{2}}$$Estilo de visualización L_{1}$$Estilo de visualización L_{2}$
• El complemento de con respecto a consta de todas las cadenas sobre que no están en .$estilo de visualización negativo L_{1}$$Estilo de visualización L_{1}$${\estilo de visualización \Sigma}$${\estilo de visualización \Sigma}$$Estilo de visualización L_{1}$
• La estrella de Kleene : el idioma que consiste en todas las palabras que son concatenaciones de cero o más palabras en el idioma original;
• Reversión :
  • Sea ε la palabra vacía, entonces , y${\displaystyle \varepsilon ^{R}=\varepsilon }$
  • para cada palabra no vacía (donde son elementos de algún alfabeto), sea ,${\displaystyle w=\sigma _{1}\cdots \sigma _{n}}$${\displaystyle \sigma _{1},\ldots ,\sigma _{n}}$${\displaystyle w^{R}=\sigma _{n}\cdots \sigma _{1}}$
  • entonces, para un lenguaje formal , .${\displaystyle L}$${\displaystyle L^{R}=\{w^{R}\mid w\in L\}}$
• Homomorfismo de cuerdas

Estas operaciones de cadenas se utilizan para investigar las propiedades de cierre de las clases de lenguajes. Una clase de lenguajes está cerrada bajo una operación particular cuando la operación, aplicada a los lenguajes de la clase, siempre produce un lenguaje de la misma clase nuevamente. Por ejemplo, se sabe que los lenguajes libres de contexto están cerrados bajo unión, concatenación e intersección con lenguajes regulares , pero no cerrados bajo intersección o complemento. La teoría de tríos y familias abstractas de lenguajes estudia las propiedades de cierre más comunes de las familias de lenguajes por derecho propio. ^[11]

Propiedades de cierre de familias lingüísticas ( Op donde tanto y están en la familia lingüística dada por la columna). Según Hopcroft y Ullman.${\displaystyle L_{1}}$${\displaystyle L_{2}}$${\displaystyle L_{1}}$${\displaystyle L_{2}}$

Operación		Regular	DCFL	Lámpara fluorescente compacta	INDIANA	CSL	recursivo	RE
Unión	${\displaystyle L_{1}\cup L_{2}=\{w\mid w\in L_{1}\lor w\in L_{2}\}}$	Sí	No	Sí	Sí	Sí	Sí	Sí
Intersección	${\displaystyle L_{1}\cap L_{2}=\{w\mid w\in L_{1}\land w\in L_{2}\}}$	Sí	No	No	No	Sí	Sí	Sí
Complementar	${\displaystyle \neg L_{1}=\{w\mid w\not \in L_{1}\}}$	Sí	Sí	No	No	Sí	Sí	No
Concatenación	${\displaystyle L_{1}\cdot L_{2}=\{wz\mid w\in L_{1}\land z\in L_{2}\}}$	Sí	No	Sí	Sí	Sí	Sí	Sí
Estrella de kleene	${\displaystyle L_{1}^{*}=\{\varepsilon \}\cup \{wz\mid w\in L_{1}\land z\in L_{1}^{*}\}}$	Sí	No	Sí	Sí	Sí	Sí	Sí
(Cadena) homomorfismo${\displaystyle h}$	${\displaystyle h(L_{1})=\{h(w)\mid w\in L_{1}\}}$	Sí	No	Sí	Sí	No	No	Sí
Homomorfismo (de cuerdas) ε-libre${\displaystyle h}$	${\displaystyle h(L_{1})=\{h(w)\mid w\in L_{1}\}}$	Sí	No	Sí	Sí	Sí	Sí	Sí
Sustitución${\displaystyle \varphi }$	${\displaystyle \varphi (L_{1})=\bigcup _{\sigma _{1}\cdots \sigma _{n}\in L_{1}}\varphi (\sigma _{1})\cdot \ldots \cdot \varphi (\sigma _{n})}$	Sí	No	Sí	Sí	Sí	No	Sí
Homomorfismo inverso${\displaystyle h^{-1}}$	${\displaystyle h^{-1}(L_{1})=\bigcup _{w\in L_{1}}h^{-1}(w)}$	Sí	Sí	Sí	Sí	Sí	Sí	Sí
Contrarrestar	${\displaystyle L^{R}=\{w^{R}\mid w\in L\}}$	Sí	No	Sí	Sí	Sí	Sí	Sí
Intersección con un lenguaje regular ${\displaystyle R}$	${\displaystyle L\cap R=\{w\mid w\in L\land w\in R\}}$	Sí	Sí	Sí	Sí	Sí	Sí	Sí

Un compilador suele tener dos componentes distintos. Un analizador léxico , a veces generado por una herramienta como lex, identifica los tokens de la gramática del lenguaje de programación, por ejemplo, identificadores o palabras clave , literales numéricos y de cadena, puntuación y símbolos de operador, que a su vez están especificados por un lenguaje formal más simple, generalmente por medio de expresiones regulares . En el nivel conceptual más básico, un analizador sintáctico , a veces generado por un generador de analizadores sintácticos como yacc, intenta decidir si el programa fuente es sintácticamente válido, es decir, si está bien formado con respecto a la gramática del lenguaje de programación para el que se construyó el compilador.

Por supuesto, los compiladores hacen más que simplemente analizar el código fuente: normalmente lo traducen a algún formato ejecutable. Por este motivo, un analizador suele generar más que una respuesta de sí o no, normalmente un árbol de sintaxis abstracta . Esto es utilizado por las etapas posteriores del compilador para generar finalmente un ejecutable que contiene código de máquina que se ejecuta directamente en el hardware, o algún código intermedio que requiere una máquina virtual para ejecutarse.

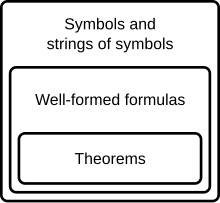
En lógica matemática , una teoría formal es un conjunto de oraciones expresadas en un lenguaje formal.

Un sistema formal (también llamado cálculo lógico o sistema lógico ) consiste en un lenguaje formal junto con un aparato deductivo (también llamado sistema deductivo ). El aparato deductivo puede consistir en un conjunto de reglas de transformación , que pueden interpretarse como reglas válidas de inferencia, o un conjunto de axiomas , o tener ambos. Un sistema formal se utiliza para derivar una expresión de una o más expresiones diferentes. Aunque un lenguaje formal se puede identificar con sus fórmulas, un sistema formal no se puede identificar igualmente por sus teoremas. Dos sistemas formales pueden tener todos los mismos teoremas y , sin embargo, diferir en algún aspecto significativo de la teoría de la prueba (una fórmula A puede ser una consecuencia sintáctica de una fórmula B en uno pero no en otro, por ejemplo).${\displaystyle {\mathcal {FS}}}$${\displaystyle {\mathcal {FS'}}}$

Una demostración formal o derivación es una secuencia finita de fórmulas bien formadas (que pueden interpretarse como oraciones o proposiciones ), cada una de las cuales es un axioma o se deduce de las fórmulas anteriores en la secuencia mediante una regla de inferencia . La última oración de la secuencia es un teorema de un sistema formal. Las demostraciones formales son útiles porque sus teoremas pueden interpretarse como proposiciones verdaderas.

Los lenguajes formales son de naturaleza completamente sintáctica, pero se les puede dar una semántica que dé significado a los elementos del lenguaje. Por ejemplo, en lógica matemática , el conjunto de fórmulas posibles de una lógica particular es un lenguaje formal, y una interpretación asigna un significado a cada una de las fórmulas, generalmente, un valor de verdad .

El estudio de las interpretaciones de los lenguajes formales se denomina semántica formal . En lógica matemática, esto se hace a menudo en términos de teoría de modelos . En la teoría de modelos, los términos que aparecen en una fórmula se interpretan como objetos dentro de estructuras matemáticas , y las reglas fijas de interpretación compositiva determinan cómo se puede derivar el valor de verdad de la fórmula a partir de la interpretación de sus términos; un modelo para una fórmula es una interpretación de términos tal que la fórmula se vuelve verdadera.

• Combinatoria sobre palabras
• Método formal
• Monoide libre
• Marco gramatical
• Notación matemática
• Cadena (informática)

Obras citadas

Referencias generales

• "Lenguaje formal", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Universidad de Maryland , Definiciones del lenguaje formal
• James Power, "Notas sobre teoría del lenguaje formal y análisis sintáctico", archivado el 21 de noviembre de 2007 en Wayback Machine , 29 de noviembre de 2002.
• Borradores de algunos capítulos del "Handbook of Formal Language Theory", vol. 1–3, G. Rozenberg y A. Salomaa (eds.), Springer Verlag , (1997):
  • Alexandru Mateescu y Arto Salomaa, “Prefacio” en el vol. 1, págs. v–viii, y “Lenguajes formales: una introducción y una sinopsis”, capítulo 1 en el vol. 1, págs. 1–39
  • Sheng Yu, "Lenguajes regulares", capítulo 2 del volumen 1
  • Jean-Michel Autebert, Jean Berstel, Luc Boasson, "Lenguajes libres de contexto y autómatas push-down", Capítulo 3 en el vol. 1
  • Christian Choffrut y Juhani Karhumäki, "Combinatoria de palabras", capítulo 6 del volumen 1
  • Tero Harju y Juhani Karhumäki, "Morfismos", Capítulo 7 en el vol. 1, págs. 439–510
  • Jean-Eric Pin, "Semigrupos sintácticos", capítulo 10 del vol. 1, págs. 679-746
  • M. Crochemore y C. Hancart, "Autómatas para la correspondencia de patrones", Capítulo 9 en el Vol. 2
  • Dora Giammarresi, Antonio Restivo, "Lenguajes bidimensionales", Capítulo 4 en vol. 3, págs. 215–267