Masa invariante
Este artículo tiene varios problemas. Ayúdenos a mejorarlo o a discutir estos problemas en la página de discusión . ( Aprenda cómo y cuándo eliminar estos mensajes )
|
La masa invariante , masa en reposo , masa intrínseca , masa propia o, en el caso de sistemas ligados, simplemente masa , es la parte de la masa total de un objeto o sistema de objetos que es independiente del movimiento general del sistema. Más precisamente, es una característica de la energía y el momento totales del sistema que es la misma en todos los marcos de referencia relacionados por transformaciones de Lorentz . [1] Si existe un marco de centro de momento para el sistema, entonces la masa invariante de un sistema es igual a su masa total en ese "marco de reposo". En otros marcos de referencia, donde el momento del sistema es distinto de cero, la masa total (también conocida como masa relativista ) del sistema es mayor que la masa invariante, pero la masa invariante permanece sin cambios.
Debido a la equivalencia masa-energía , la energía en reposo del sistema es simplemente la masa invariante multiplicada por la velocidad de la luz al cuadrado. De manera similar, la energía total del sistema es su masa total (relativista) multiplicada por la velocidad de la luz al cuadrado.
Los sistemas cuyo cuadrimpulso es un vector nulo (por ejemplo, un solo fotón o muchos fotones que se mueven exactamente en la misma dirección) tienen masa invariante cero y se los denomina sin masa . Un objeto físico o partícula que se mueve más rápido que la velocidad de la luz tendría cuadrimpulsos espaciales (como el hipotético taquión ), y estos no parecen existir. Cualquier cuadrimpulso temporal posee un marco de referencia donde el momento (tridimensional) es cero, que es un marco de centro de momento. En este caso, la masa invariante es positiva y se denomina masa en reposo.
Si los objetos dentro de un sistema están en movimiento relativo, entonces la masa invariante de todo el sistema será diferente de la suma de las masas en reposo de los objetos. Esto también es igual a la energía total del sistema dividida por c 2 . Véase equivalencia masa-energía para una discusión de las definiciones de masa. Dado que la masa de los sistemas debe medirse con un peso o una balanza de masa en un marco de centro de momento en el que todo el sistema tiene momento cero, dicha balanza siempre mide la masa invariante del sistema. Por ejemplo, una balanza mediría la energía cinética de las moléculas en una botella de gas como parte de la masa invariante de la botella y, por lo tanto, también su masa en reposo. Lo mismo es cierto para las partículas sin masa en dicho sistema, que agregan masa invariante y también masa en reposo a los sistemas, de acuerdo con su energía.
En el caso de un sistema masivo aislado , el centro de masa del sistema se mueve en línea recta con una velocidad subluminal constante (cuya velocidad depende del marco de referencia utilizado para observarlo). Por lo tanto, siempre se puede colocar un observador para que se mueva junto con él. En este marco, que es el marco del centro de momento, el momento total es cero y se puede pensar que el sistema en su conjunto está "en reposo" si es un sistema ligado (como una botella de gas). En este marco, que existe bajo estas suposiciones, la masa invariante del sistema es igual a la energía total del sistema (en el marco de momento cero) dividida por c 2 . Esta energía total en el marco del centro de momento es la energía mínima que se puede observar que tiene el sistema cuando lo ven varios observadores desde varios marcos inerciales.
Nótese que, por las razones antes mencionadas, no existe un sistema de reposo para fotones individuales o rayos de luz que se mueven en una dirección. Sin embargo, cuando dos o más fotones se mueven en direcciones diferentes, existe un sistema de centro de masas (o "sistema de reposo" si el sistema está acotado). Por lo tanto, la masa de un sistema de varios fotones que se mueven en direcciones diferentes es positiva, lo que significa que existe una masa invariante para este sistema aunque no exista para cada fotón.
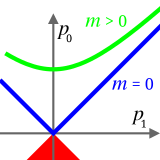
Suma de masas en reposo
La masa invariante de un sistema incluye la masa de cualquier energía cinética de los constituyentes del sistema que permanezca en el centro del marco de referencia del momento, por lo que la masa invariante de un sistema puede ser mayor que la suma de las masas invariantes (masas en reposo) de sus constituyentes separados. Por ejemplo, la masa en reposo y la masa invariante son cero para los fotones individuales, aunque puedan agregar masa a la masa invariante de los sistemas. Por esta razón, la masa invariante en general no es una cantidad aditiva (aunque existen algunas situaciones raras en las que puede serlo, como es el caso cuando las partículas masivas en un sistema sin energía potencial o cinética pueden agregarse a una masa total).
Consideremos el caso simple de un sistema de dos cuerpos, donde el objeto A se mueve hacia otro objeto B que está inicialmente en reposo (en cualquier marco de referencia particular). La magnitud de la masa invariante de este sistema de dos cuerpos (ver la definición a continuación) es diferente de la suma de la masa en reposo (es decir, su respectiva masa cuando está estacionario). Incluso si consideramos el mismo sistema desde el marco del centro del momento, donde el momento neto es cero, la magnitud de la masa invariante del sistema no es igual a la suma de las masas en reposo de las partículas dentro de él.
La energía cinética de dichas partículas y la energía potencial de los campos de fuerza aumentan la energía total por encima de la suma de las masas en reposo de las partículas, y ambos términos contribuyen a la masa invariante del sistema. La suma de las energías cinéticas de las partículas calculadas por un observador es más pequeña en el centro del marco de momento (de nuevo, llamado "marco de reposo" si el sistema está acotado).
A menudo también interactuarán a través de una o más de las fuerzas fundamentales , lo que les confiere una energía potencial de interacción, posiblemente negativa .
Como se define en la física de partículas
En física de partículas , la masa invariante m 0 es igual a la masa en el marco de reposo de la partícula, y se puede calcular mediante la energía E de la partícula y su momento p medido en cualquier marco, mediante la relación energía-momento : o en unidades naturales donde c = 1 ,
Esta masa invariante es la misma en todos los marcos de referencia (véase también relatividad especial ). Esta ecuación dice que la masa invariante es la longitud pseudoeuclidiana del cuatrivector ( E , p ) , calculada utilizando la versión relativista del teorema de Pitágoras que tiene un signo diferente para las dimensiones de espacio y tiempo. Esta longitud se conserva bajo cualquier impulso de Lorentz o rotación en cuatro dimensiones, al igual que la longitud ordinaria de un vector se conserva bajo rotaciones. En la teoría cuántica, la masa invariante es un parámetro en la ecuación relativista de Dirac para una partícula elemental. El operador cuántico de Dirac corresponde al vector de cuatro momentos de la partícula.
Dado que la masa invariante se determina a partir de cantidades que se conservan durante una desintegración, la masa invariante calculada utilizando la energía y el momento de los productos de la desintegración de una sola partícula es igual a la masa de la partícula que se desintegró. La masa de un sistema de partículas se puede calcular a partir de la fórmula general: donde
- es la masa invariante del sistema de partículas, igual a la masa de la partícula de desintegración.
- es la suma de las energías de las partículas
- es la suma vectorial del momento de las partículas (incluye tanto la magnitud como la dirección de los momentos)
El término masa invariante también se utiliza en experimentos de dispersión inelástica. Dada una reacción inelástica con una energía entrante total mayor que la energía total detectada (es decir, no se detectan todas las partículas salientes en el experimento), la masa invariante (también conocida como "masa faltante") W de la reacción se define de la siguiente manera (en unidades naturales):
Si hay una partícula dominante que no fue detectada durante un experimento, un gráfico de la masa invariante mostrará un pico pronunciado en la masa de la partícula faltante.
En aquellos casos en que no se puede medir el momento a lo largo de una dirección (es decir, en el caso de un neutrino, cuya presencia sólo se infiere a partir de la energía faltante ), se utiliza la masa transversal .
Ejemplo: colisión de dos partículas
En una colisión de dos partículas (o una desintegración de dos partículas) el cuadrado de la masa invariante (en unidades naturales ) es
Partículas sin masa
La masa invariante de un sistema formado por dos partículas sin masa cuyos momentos forman un ángulo tiene una expresión conveniente:
Experimentos con colisionadores
En los experimentos de colisionadores de partículas, a menudo se define la posición angular de una partícula en términos de un ángulo azimutal y una pseudorapidez . Además, se suele medir el momento transversal, . En este caso, si las partículas no tienen masa o son altamente relativistas ( ), entonces la masa invariante se convierte en:
Energía de descanso
La energía en reposo (también llamada energía de masa en reposo ) es la energía asociada con la masa invariante de una partícula. [2] [3]
La energía en reposo de una partícula se define como: donde es la velocidad de la luz en el vacío . [2] [3] [4] En general, solo las diferencias de energía tienen significado físico. [5]
El concepto de energía en reposo se deriva de la teoría especial de la relatividad que conduce a la famosa conclusión de Einstein sobre la equivalencia entre energía y masa. Véase Relatividad especial § Dinámica relativista e invariancia .
Véase también
Referencias
- Landau, LD; Lifshitz, EM (1975). La teoría clásica de campos: 4.ª edición revisada en inglés: Curso de física teórica, vol. 2. Butterworth Heinemann. ISBN 0-7506-2768-9.
- Halzen, Francis ; Martin, Alan (1984). Quarks y leptones: un curso introductorio a la física de partículas moderna . John Wiley & Sons . ISBN 0-471-88741-2.
Citas
- ^ Lawrence S. Lerner. Física para científicos e ingenieros, Volumen 2, página 1073. 1997.
- ^ ab Nave, CR "Energía relativista". HyperPhysics . Universidad Estatal de Georgia . Consultado el 28 de agosto de 2023 .
- ^ ab "13.6 Energía relativista o E = mc^2".
- ^ Phillip L. Reu (marzo de 2007). Desarrollo del velocímetro electrónico Doppler: teoría (PDF) (informe). Sandia National Laboratories. SAND2006-6063. Archivado desde el original (PDF) el 23 de junio de 2015.
- ^ Modell, Michael; Reid, Robert C. (1974). Termodinámica y sus aplicaciones . Englewood Cliffs, Nueva Jersey: Prentice-Hall . ISBN. 0-13-914861-2.












![{\displaystyle {\begin{aligned}M^{2}&=(E_{1}+E_{2})^{2}-\left\|{\textbf {p}}_{1}+{\ textbf {p}}_{2}\right\|^{2}\\&=[(p_{1},0,0,p_{1})+(p_{2},0,p_{2} \sin \theta ,p_{2}\cos \theta )]^{2}\\&=(p_{1}+p_{2})^{2}-p_{2}^{2}\sin ^ {2}\theta -(p_{1}+p_{2}\cos \theta )^{2}\\&=2p_{1}p_{2}(1-\cos \theta ).\end{alineado }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e86c0b0553acbe9c6e2db880847c2a04257a0dbf)







