Lógica en informática

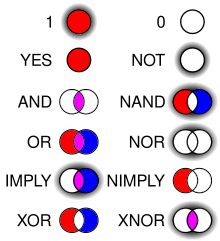
La lógica en informática cubre la superposición entre el campo de la lógica y el de la informática . El tema se puede dividir esencialmente en tres áreas principales:

• Fundamentos teóricos y análisis
• Uso de tecnología informática para ayudar a los lógicos
• Uso de conceptos de lógica para aplicaciones informáticas

La lógica juega un papel fundamental en la informática. Algunas de las áreas clave de la lógica que son particularmente significativas son la teoría de la computabilidad (antes llamada teoría de la recursión), la lógica modal y la teoría de categorías . La teoría de la computación se basa en conceptos definidos por lógicos y matemáticos como Alonzo Church y Alan Turing . ^{[1] [2]} Church fue el primero en demostrar la existencia de problemas algorítmicamente irresolubles utilizando su noción de definibilidad lambda. Turing realizó el primer análisis convincente de lo que puede llamarse un procedimiento mecánico y Kurt Gödel afirmó que encontró el análisis de Turing "perfecto". ^[3] Además, algunas otras áreas importantes de superposición teórica entre la lógica y la informática son:

• El teorema de incompletitud de Gödel demuestra que cualquier sistema lógico lo suficientemente potente como para caracterizar la aritmética contendrá afirmaciones que no pueden ser probadas ni refutadas dentro de ese sistema. Esto tiene una aplicación directa en cuestiones teóricas relacionadas con la viabilidad de probar la completitud y la corrección del software. ^[4]
• El problema del marco es un problema básico que debe superarse cuando se utiliza la lógica de primer orden para representar los objetivos de un agente de inteligencia artificial y el estado de su entorno. ^[5]
• La correspondencia Curry-Howard es una relación entre sistemas lógicos y lenguajes de programación. Esta teoría estableció una correspondencia precisa entre pruebas y programas. En particular, demostró que los términos del cálculo lambda de tipos simples corresponden a pruebas de lógica proposicional intuicionista .
• La teoría de categorías representa una visión de las matemáticas que enfatiza las relaciones entre estructuras. Está íntimamente ligada a muchos aspectos de la informática: sistemas de tipos para lenguajes de programación, la teoría de sistemas de transición , modelos de lenguajes de programación y la teoría de la semántica de los lenguajes de programación . ^[6]
• La programación lógica es un paradigma de programación , base de datos y representación del conocimiento que se basa en la lógica formal . Un programa lógico es un conjunto de oraciones sobre un dominio de problemas. El cálculo se realiza aplicando el razonamiento lógico para resolver problemas en el dominio. Las principales familias de lenguajes de programación lógica incluyen Prolog , Answer Set Programming (ASP) y Datalog .

Una de las primeras aplicaciones en las que se utilizó el término inteligencia artificial fue el sistema Logic Theorist desarrollado por Allen Newell , Cliff Shaw y Herbert Simon en 1956. Una de las cosas que hace un lógico es tomar un conjunto de afirmaciones en lógica y deducir las conclusiones (afirmaciones adicionales) que deben ser verdaderas según las leyes de la lógica. Por ejemplo, si se dan las afirmaciones "Todos los humanos son mortales" y "Sócrates es humano", una conclusión válida es "Sócrates es mortal". Por supuesto, este es un ejemplo trivial. En los sistemas lógicos reales, las afirmaciones pueden ser numerosas y complejas. Se comprendió desde el principio que este tipo de análisis podría verse significativamente facilitado por el uso de computadoras. Logic Theorist validó el trabajo teórico de Bertrand Russell y Alfred North Whitehead en su influyente trabajo sobre lógica matemática llamado Principia Mathematica . Además, los lógicos han utilizado sistemas posteriores para validar y descubrir nuevos teoremas y pruebas matemáticas. ^[7]

La lógica matemática siempre ha ejercido una fuerte influencia en el campo de la inteligencia artificial (IA). Desde el comienzo de este campo, se comprendió que la tecnología para automatizar inferencias lógicas podría tener un gran potencial para resolver problemas y extraer conclusiones de los hechos. Ron Brachman ha descrito la lógica de primer orden (FOL) como la métrica con la que se deben evaluar todos los formalismos de representación del conocimiento de la IA . La lógica de primer orden es un método general y poderoso para describir y analizar información. La razón por la que la FOL en sí misma simplemente no se utiliza como lenguaje informático es que, en realidad, es demasiado expresiva , en el sentido de que puede expresar fácilmente afirmaciones que ninguna computadora, por potente que sea, podría resolver jamás. Por esta razón, toda forma de representación del conocimiento es, en cierto sentido, un equilibrio entre expresividad y computabilidad . Cuanto más expresivo sea el lenguaje, cuanto más se acerque a la FOL, más probabilidades hay de que sea más lento y propenso a un bucle infinito. ^[8]

Por ejemplo, las reglas IF-THEN utilizadas en sistemas expertos se aproximan a un subconjunto muy limitado de FOL. En lugar de fórmulas arbitrarias con toda la gama de operadores lógicos, el punto de partida es simplemente lo que los lógicos denominan modus ponens . Como resultado, los sistemas basados ​​en reglas pueden soportar cálculos de alto rendimiento, especialmente si aprovechan los algoritmos de optimización y la compilación. ^[9]

Por otra parte, la programación lógica , que combina el subconjunto de cláusulas de Horn de la lógica de primer orden con una forma no monótona de negación , tiene tanto un alto poder expresivo como implementaciones eficientes . En particular, el lenguaje de programación lógica Prolog es un lenguaje de programación completo de Turing . Datalog extiende el modelo de base de datos relacional con relaciones recursivas, mientras que la programación de conjuntos de respuestas es una forma de programación lógica orientada a problemas de búsqueda difíciles (principalmente NP-hard ) .

Otro campo importante de investigación de la teoría lógica es la ingeniería de software . Proyectos de investigación como el Asistente de Software Basado en Conocimiento y los programas Aprendiz de Programador han aplicado la teoría lógica para validar la exactitud de las especificaciones de software . También han utilizado herramientas lógicas para transformar las especificaciones en código eficiente en diversas plataformas y para demostrar la equivalencia entre la implementación y la especificación. ^[10] Este enfoque formal impulsado por la transformación suele requerir mucho más esfuerzo que el desarrollo de software tradicional. Sin embargo, en dominios específicos con formalismos apropiados y plantillas reutilizables, el enfoque ha demostrado ser viable para productos comerciales. Los dominios apropiados suelen ser aquellos como los sistemas de armas, los sistemas de seguridad y los sistemas financieros en tiempo real donde el fallo del sistema tiene un coste humano o financiero excesivamente alto. Un ejemplo de un dominio de este tipo es el diseño integrado a muy gran escala (VLSI) , el proceso para diseñar los chips utilizados para las CPU y otros componentes críticos de los dispositivos digitales. Un error en un chip puede ser catastrófico. A diferencia del software, los chips no se pueden parchear ni actualizar. Como resultado, existe una justificación comercial para utilizar métodos formales para demostrar que la implementación corresponde a la especificación. ^[11]

Otra aplicación importante de la lógica a la tecnología informática ha sido en el área de los lenguajes de marco y los clasificadores automáticos. Los lenguajes de marco como KL-ONE se pueden mapear directamente a la teoría de conjuntos y la lógica de primer orden. Esto permite que los probadores de teoremas especializados llamados clasificadores analicen las diversas declaraciones entre conjuntos , subconjuntos y relaciones en un modelo dado. De esta manera, el modelo se puede validar y cualquier definición inconsistente se puede marcar. El clasificador también puede inferir nueva información, por ejemplo, definir nuevos conjuntos basados ​​en información existente y cambiar la definición de conjuntos existentes en función de nuevos datos. El nivel de flexibilidad es ideal para manejar el mundo en constante cambio de Internet. La tecnología de clasificadores se basa en lenguajes como el lenguaje de ontología web para permitir un nivel semántico lógico sobre la Internet existente. Esta capa se llama Web semántica . ^{[12] [13]}

La lógica temporal se utiliza para razonar en sistemas concurrentes . ^[14]

• Razonamiento automatizado
• Lógica computacional
• Programación lógica

• Ben-Ari, Mordechai (2012). Lógica matemática para la informática (3.ª ed.). Springer-Verlag. ISBN 978-1447141280.
• Harrison, John (2009). Manual de lógica práctica y razonamiento automatizado (1.ª ed.). Cambridge University Press. ISBN 978-0521899574.
• Huth, Michael; Ryan, Mark (2004). Lógica en informática: modelado y razonamiento sobre sistemas (2.ª ed.). Cambridge University Press. ISBN 978-0521543101.
• Burris, Stanley N. (1997). Lógica para matemáticas y ciencias de la computación (1.ª ed.). Prentice Hall. ISBN 978-0132859745.

• Artículo sobre lógica e inteligencia artificial en la Enciclopedia de Filosofía de Stanford .
• Simposio IEEE sobre lógica en informática (LICS)
• Alwen Tiu, Introducción a la lógica, grabación en video de una conferencia en la Escuela de verano de lógica de la ANU '09 (dirigida principalmente a científicos informáticos)