Identidad (matemáticas)

En matemáticas , una identidad es una igualdad que relaciona una expresión matemática A  con otra expresión matemática  B , de modo que A y B (que pueden contener algunas variables ) producen el mismo valor para todos los valores de las variables dentro de un cierto dominio del discurso . ^{[1] [2]} En otras palabras, A  =  B es una identidad si A y B definen las mismas funciones , y una identidad es una igualdad entre funciones que se definen de manera diferente. Por ejemplo, y son identidades. ^[3] Las identidades a veces se indican con el símbolo de triple barra ≡ en lugar de = , el signo igual . ^[4] Formalmente, una identidad es una igualdad cuantificada universalmente .${\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}$${\displaystyle \cos ^{2}\theta +\sin ^{2}\theta = 1}$

Ciertas identidades, como y , forman la base del álgebra , ^[5] mientras que otras identidades, como y , pueden ser útiles para simplificar expresiones algebraicas y expandirlas. ^[6]${\displaystyle a+0=a}$${\displaystyle a+(-a)=0}$${\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}$${\displaystyle a^{2}-b^{2}=(a+b)(ab)}$

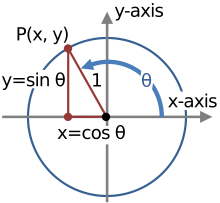
Geométricamente, las identidades trigonométricas son identidades que involucran ciertas funciones de uno o más ángulos . ^[7] Son distintas de las identidades triangulares , que son identidades que involucran tanto los ángulos como las longitudes de los lados de un triángulo . En este artículo solo se tratan las primeras.

Estas identidades son útiles siempre que sea necesario simplificar expresiones que involucran funciones trigonométricas. Otra aplicación importante es la integración de funciones no trigonométricas: una técnica común que implica primero usar la regla de sustitución con una función trigonométrica y luego simplificar la integral resultante con una identidad trigonométrica.

Uno de los ejemplos más destacados de identidades trigonométricas implica la ecuación que es verdadera para todos los valores reales de . Por otro lado, la ecuación${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta = 1,}$${\estilo de visualización \theta}$

${\displaystyle \cos \theta = 1}$

solo es verdadera para ciertos valores de , no para todos. Por ejemplo, esta ecuación es verdadera cuando pero falsa cuando .${\estilo de visualización \theta}$${\displaystyle \theta = 0,}$${\displaystyle \theta = 2}$

Otro grupo de identidades trigonométricas se refiere a las llamadas fórmulas de suma/resta (por ejemplo, la identidad del ángulo doble , la fórmula de adición para ), que pueden utilizarse para descomponer expresiones de ángulos mayores en aquellas con constituyentes más pequeños.${\displaystyle \sin(2\theta )=2\sin \theta \cos \theta }$$Estilo de visualización: tan(x+y)$

Las siguientes identidades son válidas para todos los exponentes enteros , siempre que la base no sea cero:

${\displaystyle {\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\(b^{m})^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}}$

A diferencia de la suma y la multiplicación, la exponenciación no es conmutativa . Por ejemplo, 2 + 3 = 3 + 2 = 5 y 2 · 3 = 3 · 2 = 6 , pero 2 ³ = 8 mientras que 3 ² = 9 .

Además, a diferencia de la suma y la multiplicación, la exponenciación tampoco es asociativa . Por ejemplo, (2 + 3) + 4 = 2 + (3 + 4) = 9 y (2 · 3) · 4 = 2 · (3 · 4) = 24 , pero 2 ^{3 elevado} a 4 es 8 ⁴ (o 4096), mientras que 2 elevado a 3 ⁴ es 2 ⁸¹ (o 2 417 851 639 229 258 349 412 352). Cuando no se escriben paréntesis, por convención el orden es de arriba hacia abajo, no de abajo hacia arriba:

${\displaystyle b^{p^{q}}:=b^{(p^{q})},}$   mientras   ${\displaystyle (b^{p})^{q}=b^{p\cdot q}.}$

Varias fórmulas importantes, a veces llamadas identidades logarítmicas o leyes logarítmicas , relacionan los logaritmos entre sí: ^[a]

El logaritmo de un producto es la suma de los logaritmos de los números que se multiplican; el logaritmo de la razón de dos números es la diferencia de los logaritmos. El logaritmo de la potencia p de un número es p por el logaritmo del número mismo; el logaritmo de una raíz p es el logaritmo del número dividido por p . La siguiente tabla enumera estas identidades con ejemplos. Cada una de las identidades se puede derivar después de la sustitución de las definiciones de logaritmo y/o en los lados izquierdos.${\displaystyle x=b^{\log _{b}x},}$${\displaystyle y=b^{\log _{b}y},}$

	Fórmula	Ejemplo
producto	${\displaystyle \log_{b}(xy)=\log_{b}(x)+\log_{b}(y)}$	${\displaystyle \log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5}$
cociente	${\displaystyle \log _{b}\!\left({\frac {x}{y}}\right)=\log _{b}(x)-\log _{b}(y)}$	${\displaystyle \log _{2}(16)=\log _{2}\!\left({\frac {64}{4}}\right)=\log _{2}(64)-\log _{2}(4)=6-2=4}$
fuerza	${\displaystyle \log_{b}(x^{p})=p\log_{b}(x)}$	${\displaystyle \log _{2}(64)=\log _{2}(2^{6})=6\log _{2}(2)=6}$
raíz	${\displaystyle \log _{b}\!{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}}$	${\displaystyle \log _{10}\!{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5}$

El logaritmo log _b ( x ) se puede calcular a partir de los logaritmos de x y b con respecto a una base arbitraria k utilizando la siguiente fórmula:

${\displaystyle \log _{b}(x)={\frac {\log _{k}(x)}{\log _{k}(b)}}.}$

Las calculadoras científicas típicas calculan los logaritmos en base 10 y e . ^[8] Los logaritmos con respecto a cualquier base b se pueden determinar utilizando cualquiera de estos dos logaritmos mediante la fórmula anterior:

${\displaystyle \log _{b}(x)={\frac {\log _{10}(x)}{\log _{10}(b)}}={\frac {\log _{e}(x)}{\log _{e}(b)}}.}$

Dado un número x y su logaritmo log _b ( x ) elevado a una base desconocida b , la base viene dada por:

${\displaystyle b=x^{\frac {1}{\log _{b}(x)}}.}$

Las funciones hiperbólicas satisfacen muchas identidades, todas ellas similares en su forma a las identidades trigonométricas . De hecho, la regla de Osborn ^[9] establece que se puede convertir cualquier identidad trigonométrica en una identidad hiperbólica desarrollándola completamente en términos de potencias enteras de senos y cosenos, cambiando seno por senh y coseno por cosh, y cambiando el signo de cada término que contenga un producto de un número par de senos hiperbólicos. ^[10]

La función Gudermanniana da una relación directa entre las funciones trigonométricas y las hiperbólicas que no involucra números complejos .

Formalmente, una identidad es una fórmula cuantificada universalmente verdadera de la forma donde s y t son términos sin otras variables libres que El prefijo cuantificador a menudo se deja implícito cuando se afirma que la fórmula es una identidad. Por ejemplo, los axiomas de un monoide a menudo se dan como fórmulas${\displaystyle \forall x_{1},\ldots ,x_{n}:s=t,}$${\displaystyle x_{1},\ldots ,x_{n}.}$${\displaystyle \forall x_{1},\ldots ,x_{n}}$

${\displaystyle \forall x,y,z:x*(y*z)=(x*y)*z,\quad \forall x:x*1=x,\quad \forall x:1*x=x,}$

o, en breve,

${\displaystyle x*(y*z)=(x*y)*z,\qquad x*1=x,\qquad 1*x=x.}$

Por lo tanto, estas fórmulas son identidades en cada monoide. Como en el caso de cualquier igualdad, las fórmulas sin cuantificador suelen denominarse ecuaciones . En otras palabras, una identidad es una ecuación que es verdadera para todos los valores de las variables. ^{[11] [12]}

• Identidad contable
• Lista de identidades matemáticas
• Derecho (matemáticas)

• La enciclopedia de ecuaciones Enciclopedia en línea de identidades matemáticas (archivada)
• Una colección de identidades algebraicas Archivado el 1 de octubre de 2011 en Wayback Machine