Estática comparativa

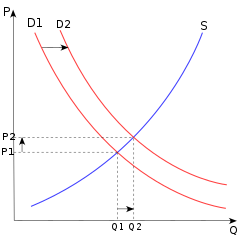
En economía , la estática comparativa es la comparación de dos resultados económicos diferentes, antes y después de un cambio en algún parámetro exógeno subyacente . ^[1]

Como tipo de análisis estático, compara dos estados de equilibrio diferentes , después del proceso de ajuste (si lo hay). No estudia el movimiento hacia el equilibrio ni el proceso de cambio en sí.

La estática comparativa se utiliza habitualmente para estudiar los cambios en la oferta y la demanda cuando se analiza un mercado único , y para estudiar los cambios en la política monetaria o fiscal cuando se analiza la economía en su conjunto . La estática comparativa es una herramienta de análisis en microeconomía (incluido el análisis de equilibrio general ) y macroeconomía . La estática comparativa fue formalizada por John R. Hicks (1939) y Paul A. Samuelson (1947) (Kehoe, 1987, p. 517), pero se presentó gráficamente al menos desde la década de 1870. ^[2]

Para los modelos de tasas de cambio de equilibrio estable, como el modelo de crecimiento neoclásico , la dinámica comparativa es la contraparte de la estática comparativa (Eatwell, 1987).

Los resultados de estática comparativa se obtienen generalmente utilizando el teorema de la función implícita para calcular una aproximación lineal al sistema de ecuaciones que define el equilibrio, bajo el supuesto de que el equilibrio es estable. Es decir, si consideramos un cambio suficientemente pequeño en algún parámetro exógeno, podemos calcular cómo cambia cada variable endógena utilizando únicamente las primeras derivadas de los términos que aparecen en las ecuaciones de equilibrio.

Por ejemplo, supongamos que el valor de equilibrio de alguna variable endógena está determinado por la siguiente ecuación:${\estilo de visualización x}$

${\displaystyle f(x,a)=0\,}$

donde es un parámetro exógeno. Entonces, en una aproximación de primer orden, el cambio en causado por un pequeño cambio en debe satisfacer:${\estilo de visualización a}$${\estilo de visualización x}$${\estilo de visualización a}$

${\displaystyle B{\text{d}}x+C{\text{d}}a=0.}$

Aquí y representan los cambios en y , respectivamente, mientras que y son las derivadas parciales de con respecto a y (evaluadas en los valores iniciales de y ), respectivamente. De manera equivalente, podemos escribir el cambio en como:${\displaystyle {\text{d}}x}$${\displaystyle {\text{d}}a}$${\estilo de visualización x}$${\estilo de visualización a}$${\estilo de visualización B}$${\estilo de visualización C}$${\estilo de visualización f}$${\estilo de visualización x}$${\estilo de visualización a}$${\estilo de visualización x}$${\estilo de visualización a}$${\estilo de visualización x}$

${\displaystyle {\text{d}}x=-B^{-1}C{\text{d}}a.}$

Dividiendo la última ecuación por d a se obtiene la derivada estática comparativa de x con respecto a a , también llamada multiplicador de a sobre x :

${\displaystyle {\frac {{\text{d}}x}{{\text{d}}a}}=-B^{-1}C.}$

Todas las ecuaciones anteriores siguen siendo verdaderas en el caso de un sistema de ecuaciones en incógnitas. En otras palabras, supongamos que representa un sistema de ecuaciones que involucra el vector de incógnitas , y el vector de parámetros dados . Si hacemos un cambio suficientemente pequeño en los parámetros, entonces los cambios resultantes en las variables endógenas pueden aproximarse arbitrariamente bien por . En este caso, representa la matriz × de derivadas parciales de las funciones con respecto a las variables , y representa la matriz × de derivadas parciales de las funciones con respecto a los parámetros . (Las derivadas en y se evalúan en los valores iniciales de y .) Nótese que si uno quiere solo el efecto estático comparativo de una variable exógena en una variable endógena, la Regla de Cramer se puede usar en el sistema de ecuaciones totalmente diferenciado .${\estilo de visualización n}$${\estilo de visualización n}$${\displaystyle f(x,a)=0}$${\estilo de visualización n}$${\estilo de visualización n}$${\estilo de visualización x}$${\estilo de visualización m}$${\estilo de visualización a}$${\displaystyle {\text{d}}a}$${\displaystyle {\text{d}}x=-B^{-1}C{\text{d}}a}$${\estilo de visualización B}$${\estilo de visualización n}$${\estilo de visualización n}$ ${\estilo de visualización f}$${\estilo de visualización x}$${\estilo de visualización C}$${\estilo de visualización n}$${\estilo de visualización m}$${\estilo de visualización f}$${\estilo de visualización a}$${\estilo de visualización B}$${\estilo de visualización C}$${\estilo de visualización x}$${\estilo de visualización a}$${\displaystyle B{\text{d}}x+C{\text{d}}a\,=0}$

El supuesto de que el equilibrio es estable es importante por dos razones. En primer lugar, si el equilibrio fuera inestable, un pequeño cambio de parámetro podría causar un gran salto en el valor de , invalidando el uso de una aproximación lineal. Además, el principio de correspondencia de Paul A. Samuelson ^{[3] [4] [5] : pp.122–123.} establece que la estabilidad del equilibrio tiene implicaciones cualitativas sobre los efectos de estática comparativa. En otras palabras, saber que el equilibrio es estable puede ayudarnos a predecir si cada uno de los coeficientes en el vector es positivo o negativo. Específicamente, una de las n condiciones necesarias y conjuntamente suficientes para la estabilidad es que el determinante de la matriz n × n B tenga un signo particular; dado que este determinante aparece como denominador en la expresión para , el signo del determinante influye en los signos de todos los elementos del vector de efectos de estática comparativa.${\estilo de visualización x}$$Estilo de visualización B-1C$$Estilo de visualización B-1$${\displaystyle B^{-1}C{\text{d}}a}$

Supongamos que las cantidades demandadas y ofrecidas de un producto están determinadas por las siguientes ecuaciones:

${\displaystyle Q^{d}(P)=a+bP}$

${\displaystyle Q^{s}(P)=c+gP}$

donde es la cantidad demandada, es la cantidad ofrecida, P es el precio, a y c son parámetros de intersección determinados por influencias exógenas sobre la demanda y la oferta respectivamente, b < 0 es el recíproco de la pendiente de la curva de demanda y g es el recíproco de la pendiente de la curva de oferta; g > 0 si la curva de oferta tiene pendiente positiva, g = 0 si la curva de oferta es vertical y g < 0 si la curva de oferta tiene pendiente negativa. Si igualamos la cantidad ofrecida con la cantidad demandada para hallar el precio de equilibrio , encontramos que${\displaystyle Q^{d}}$${\displaystyle Q^{s}}$${\displaystyle P^{eqb}}$

${\displaystyle P^{eqb}={\frac {ac}{gb}}.}$

Esto significa que el precio de equilibrio depende positivamente de la intersección de la demanda si g – b > 0, pero depende negativamente de ella si g – b < 0. ¿Cuál de estas posibilidades es relevante? De hecho, partiendo de un equilibrio estático inicial y luego cambiando a , el nuevo equilibrio es relevante solo si el mercado realmente va a ese nuevo equilibrio. Supongamos que los ajustes de precios en el mercado ocurren de acuerdo con

${\displaystyle {\frac {dP}{dt}}=\lambda (Q^{d}(P)-Q^{s}(P))}$

donde > 0 es el parámetro de velocidad de ajuste y es la derivada temporal del precio, es decir, indica qué tan rápido y en qué dirección cambia el precio. Según la teoría de la estabilidad , P convergerá a su valor de equilibrio si y solo si la derivada es negativa. Esta derivada está dada por${\estilo de visualización \lambda}$${\displaystyle {\frac {dP}{dt}}}$ ${\displaystyle {\frac {d(dP/dt)}{dP}}}$

${\displaystyle {\frac {d(dP/dt)}{dP}}=-\lambda (-b+g).}$

Esto es negativo si y solo si g – b > 0, en cuyo caso el parámetro de intersección de la demanda a influye positivamente en el precio. Por lo tanto, podemos decir que, si bien la dirección del efecto de la intersección de la demanda sobre el precio de equilibrio es ambigua cuando todo lo que sabemos es que el recíproco de la pendiente de la curva de oferta, g , es negativo, en el único caso relevante (en el que el precio realmente va a su nuevo valor de equilibrio) un aumento en la intersección de la demanda aumenta el precio. Nótese que este caso, con g – b > 0, es el caso en el que la curva de oferta, si tiene pendiente negativa, es más pronunciada que la curva de demanda.

Supongamos que es una función objetivo suave y estrictamente cóncava donde x es un vector de n variables endógenas y q es un vector de m parámetros exógenos. Consideremos el problema de optimización sin restricciones . Sea , la matriz n por n de primeras derivadas parciales de con respecto a sus primeros n argumentos x ₁ ,..., x _n . El maximizador está definido por la condición de primer orden n ×1 .${\displaystyle p(x;q)}$${\displaystyle x^{*}(q)=\arg \max p(x;q)}$${\displaystyle f(x;q)=D_{x}p(x;q)}$${\displaystyle p(x;q)}$${\displaystyle x^{*}(q)}$${\displaystyle f(x^{*}(q);q)=0}$

La estática comparativa pregunta cómo cambia este maximizador en respuesta a los cambios en los parámetros m . El objetivo es encontrar .${\displaystyle \parcial x_{i}^{*}/\parcial q_{j},i=1,...,n,j=1,...,m}$

La concavidad estricta de la función objetivo implica que el jacobiano de f , que es exactamente la matriz de derivadas parciales segundas de p con respecto a las variables endógenas, no es singular (tiene una inversa). Por el teorema de la función implícita , entonces, puede verse localmente como una función continuamente diferenciable, y la respuesta local de a pequeños cambios en q está dada por ${\displaystyle x^{*}(q)}$${\displaystyle x^{*}(q)}$

${\displaystyle D_{q}x^{*}(q)=-[D_{x}f(x^{*}(q);q)]^{-1}D_{q}f(x^{*}(q);q).}$

Aplicando la regla de la cadena y la condición de primer orden,

${\displaystyle D_{q}p(x^{*}(q),q)=D_{q}p(x;q)|_{x=x^{*}(q)}.}$

(Véase Teorema de la envolvente ).

Supongamos que una empresa produce n bienes en cantidades . La utilidad de la empresa es una función p de y de m parámetros exógenos que pueden representar, por ejemplo, diversas tasas impositivas. Siempre que la función de utilidad satisfaga los requisitos de suavidad y concavidad, el método de estática comparativa descrito anteriormente describe los cambios en la utilidad de la empresa debido a pequeños cambios en las tasas impositivas.${\displaystyle x_{1},...,x_{n}}$${\displaystyle x_{1},...,x_{n}}$${\displaystyle q_{1},...,q_{m}}$

Una generalización del método anterior permite que el problema de optimización incluya un conjunto de restricciones. Esto conduce al teorema de la envolvente general . Las aplicaciones incluyen la determinación de cambios en la demanda marshalliana en respuesta a cambios en el precio o el salario.

Una limitación de la estática comparativa que utiliza el teorema de la función implícita es que los resultados son válidos sólo en un entorno (potencialmente muy pequeño) del óptimo, es decir, sólo para cambios muy pequeños en las variables exógenas. Otra limitación es la naturaleza potencialmente demasiado restrictiva de los supuestos que se utilizan convencionalmente para justificar los procedimientos de estática comparativa. Por ejemplo, John Nachbar descubrió en uno de sus estudios de caso que el uso de la estática comparativa en el análisis del equilibrio general funciona mejor con un nivel muy pequeño de datos individuales que a un nivel agregado. ^[6]

Paul Milgrom y Chris Shannon ^[7] señalaron en 1994 que los supuestos utilizados convencionalmente para justificar el uso de la estática comparativa en problemas de optimización no son realmente necesarios, específicamente, los supuestos de convexidad de conjuntos preferidos o conjuntos de restricciones, suavidad de sus límites, condiciones de primera y segunda derivadas y linealidad de conjuntos presupuestarios o funciones objetivo. De hecho, a veces un problema que cumple con estas condiciones puede transformarse monótonamente para dar un problema con estática comparativa idéntica pero que viola algunas o todas estas condiciones; por lo tanto, estas condiciones no son necesarias para justificar la estática comparativa. A partir del artículo de Milgrom y Shannon, así como de los resultados obtenidos por Veinott ^[8] y Topkis ^[9], se desarrolló una importante línea de investigación operativa llamada estática comparativa monótona . En particular, esta teoría se concentra en el análisis de estática comparativa utilizando solo condiciones que son independientes de las transformaciones que preservan el orden. El método utiliza la teoría de celosía e introduce las nociones de cuasi-supermodularidad y la condición de cruce simple. La amplia aplicación de la estática comparativa monótona a la economía incluye la teoría de la producción, la teoría del consumidor, la teoría de juegos con información completa e incompleta, la teoría de subastas y otras. ^[10]

• Modelo (economía)
• Economía cualitativa

• John Eatwell et al., ed. (1987). "Dinámica comparativa", The New Palgrave: A Dictionary of Economics , vol. 1, pág. 517.
• John R. Hicks (1939). Valor y capital .
• Timothy J. Kehoe, 1987. "Estática comparativa", The New Palgrave: A Dictionary of Economics , v. 1, págs. 517-20.
• Andreu Mas-Colell , Michael D. Whinston y Jerry R. Green, 1995. Teoría microeconómica .
• Paul A. Samuelson (1947). Fundamentos del análisis económico .
• Eugene Silberberg y Wing Suen, 2000. La estructura de la economía: un análisis matemático , 3ª edición.

• Departamento de Economía de la Universidad Estatal de San José: Análisis de estática comparativa
• Glosario de AmosWeb
• Glosario del Instituto de Riesgos IFCI (del glosario de la Bolsa de Valores de Estados Unidos ) [1]