Energía superficial

Exceso de energía en la superficie de un material con respecto a su interior.

En la ciencia de superficies , la energía superficial (también energía libre interfacial o energía libre superficial ) cuantifica la interrupción de los enlaces intermoleculares que se produce cuando se crea una superficie . En la física del estado sólido , las superficies deben ser intrínsecamente menos favorables energéticamente que la masa del material (es decir, los átomos de la superficie deben tener más energía que los átomos de la masa); de lo contrario, habría una fuerza impulsora para que se crearan superficies, eliminando la masa del material por sublimación . Por lo tanto, la energía superficial puede definirse como el exceso de energía en la superficie de un material en comparación con la masa, o es el trabajo necesario para construir un área de una superficie particular. Otra forma de ver la energía superficial es relacionarla con el trabajo necesario para cortar una muestra a granel, creando dos superficies. Hay "exceso de energía" como resultado de la unión ahora incompleta y no realizada entre las dos superficies creadas.

Cortar un cuerpo sólido en pedazos rompe sus enlaces y aumenta el área de superficie, y por lo tanto aumenta la energía superficial. Si el corte se hace de manera reversible , entonces la conservación de la energía significa que la energía consumida por el proceso de corte será igual a la energía inherente a las dos nuevas superficies creadas. La energía superficial unitaria de un material sería, por lo tanto, la mitad de su energía de cohesión , siendo todo lo demás igual; en la práctica, esto es cierto solo para una superficie recién preparada al vacío . Las superficies a menudo cambian su forma alejándose del modelo simple de " enlace escindido " que acabamos de insinuar. Se ha descubierto que son regiones altamente dinámicas, que se reorganizan o reaccionan fácilmente , de modo que la energía a menudo se reduce mediante procesos como la pasivación o la adsorción .

Evaluación

Medición

Angulo de contacto

La forma más común de medir la energía superficial es a través de experimentos de ángulo de contacto . ^[1] En este método, el ángulo de contacto de la superficie se mide con varios líquidos, generalmente agua y diyodometano . En función de los resultados del ángulo de contacto y conociendo la tensión superficial de los líquidos, se puede calcular la energía superficial. En la práctica, este análisis se realiza automáticamente mediante un medidor de ángulo de contacto. ^[2]

Existen varios modelos diferentes para calcular la energía superficial basándose en las lecturas del ángulo de contacto. ^[3] El método más comúnmente utilizado es OWRK, que requiere el uso de dos líquidos de sonda y proporciona como resultado la energía superficial total y la divide en componentes polares y dispersivos.

El método del ángulo de contacto es el método estándar de medición de energía superficial debido a su simplicidad, aplicabilidad a una amplia gama de superficies y rapidez. La medición puede automatizarse por completo y está estandarizada. ^[4]

En general, a medida que aumenta la energía superficial, el ángulo de contacto disminuye porque la superficie "agarra" más líquido. Por el contrario, a medida que disminuye la energía superficial, el ángulo de contacto aumenta, porque la superficie no quiere interactuar con el líquido.

Otros métodos

La energía superficial de un líquido se puede medir estirando una membrana líquida (lo que aumenta el área superficial y, por lo tanto, la energía superficial). En ese caso, para aumentar el área superficial de una masa de líquido en una cantidad, $δA$ , se necesita una cantidad de trabajo , $γ δA$ , (donde $γ$ es la densidad de energía superficial del líquido). Sin embargo, dicho método no se puede utilizar para medir la energía superficial de un sólido porque el estiramiento de una membrana sólida induce energía elástica en la masa además de aumentar la energía superficial.

La energía superficial de un sólido se mide normalmente a altas temperaturas. A tales temperaturas, el sólido se desliza y, aunque el área superficial cambia, el volumen permanece aproximadamente constante. Si $γ$ es la densidad de energía superficial de una varilla cilíndrica de radio $r$ y longitud $l$ a alta temperatura y una tensión uniaxial constante $P$ , entonces, en equilibrio, la variación de la energía libre total de Helmholtz se desvanece y tenemos

\delta F=-P~\delta l+\gamma ~\delta A=0\quad \implica \quad \gamma =P{\frac {\delta l}{\delta A}}

donde $F$ es la energía libre de Helmholtz y $A$ es el área superficial de la varilla:

A=2\pi r^{2}+2\pi rl\quad \implica \quad \delta A=4\pi r\delta r+2\pi l\delta r+2\pi r\delta l

Además, como el volumen ( $V$ ) de la varilla permanece constante, la variación ( $δV$ ) del volumen es cero, es decir,

V=\pi r^{2}l{\text{ es constante}}\quad \implies \quad \delta V=2\pi rl\delta r+\pi r^{2}\delta l=0\quad \implies \quad \delta r=-{\frac {r}{2l}}\delta l~.

Por lo tanto, la densidad de energía superficial se puede expresar como

\gamma ={\frac {Pl}{\pi r(l-2r)}}~.

La densidad de energía superficial del sólido se puede calcular midiendo $P$ , $r$ y $l$ en equilibrio.

Este método es válido únicamente si el sólido es isotrópico , es decir, la energía superficial es la misma para todas las orientaciones cristalográficas . Si bien esto es estrictamente cierto solo para sólidos amorfos ( vidrio ) y líquidos, la isotropía es una buena aproximación para muchos otros materiales. En particular, si la muestra es poligranular (la mayoría de los metales) o está hecha mediante sinterización de polvo (la mayoría de las cerámicas), esta es una buena aproximación.

En el caso de materiales monocristalinos, como las piedras preciosas naturales , la anisotropía en la energía superficial conduce al tallado . La forma del cristal (suponiendo condiciones de crecimiento en equilibrio ) está relacionada con la energía superficial mediante la construcción de Wulff . La energía superficial de las facetas se puede encontrar, por tanto, dentro de una constante de escala midiendo los tamaños relativos de las facetas.

Cálculo

Sólido deformado

En la deformación de sólidos, la energía superficial puede tratarse como la "energía requerida para crear una unidad de área superficial", y es una función de la diferencia entre las energías totales del sistema antes y después de la deformación:

\gamma ={\frac {1}{A}}\left(E_{1}-E_{0}\right)

.

El cálculo de la energía superficial a partir de principios básicos (por ejemplo, la teoría del funcional de la densidad ) es un enfoque alternativo para la medición. La energía superficial se estima a partir de las siguientes variables: ancho de la banda d, número de electrones d de valencia y número de coordinación de átomos en la superficie y en la masa del sólido. ^[5]^{[ página necesaria ]}

Energía de formación de superficie de un sólido cristalino

En la teoría del funcional de la densidad , la energía superficial se puede calcular a partir de la siguiente expresión:

\gamma ={\frac {E_{\text{losa}}-NE_{\text{volumen}}}{2A}}

dónde

E losa

es la energía total de la losa superficial obtenida utilizando la teoría del funcional de la densidad.

N

es el número de átomos en la placa superficial.

E bulk

es la energía en masa por átomo.

A

es el área de la superficie.

En el caso de una losa, tenemos dos superficies y son del mismo tipo, lo que se refleja en el número 2 en el denominador. Para garantizar esto, debemos crear la losa con cuidado para asegurarnos de que las superficies superior e inferior sean del mismo tipo.

La fuerza de los contactos adhesivos se determina por el trabajo de adhesión, que también se denomina energía superficial relativa de dos cuerpos en contacto. ^[6]^{[ página necesaria ]} La energía superficial relativa se puede determinar separando cuerpos de forma bien definida hechos de un material del sustrato hecho del segundo material. ^[7] Por ejemplo, la energía superficial relativa de la interfaz " vidrio acrílico - gelatina " es igual a 0,03 N/m. La configuración experimental para medir la energía superficial relativa y su función se pueden ver en el video. ^[8]

Estimación a partir del calor de sublimación

Para estimar la energía superficial de un material puro y uniforme, se puede modelar una región individual del material como un cubo. Para mover un cubo desde el volumen de un material hasta la superficie, se requiere energía. Este costo de energía se incorpora a la energía superficial del material, que se cuantifica mediante:

Modelo cúbico. El modelo cúbico se puede utilizar para modelar materiales puros y uniformes o un componente molecular individual para estimar su energía superficial.

\gamma ={\frac {\left(z_{\sigma }-z_{\beta }\right){\frac {1}{2}}W_{\text{AA}}}{a_{0}}}

donde $z σ$ y $z β$ son números de coordinación correspondientes a las regiones superficiales y en masa del material, y son iguales a 5 y 6, respectivamente; $a 0$ es el área superficial de una molécula individual, y $W AA$ es la energía intermolecular por pares.

El área de superficie se puede determinar elevando al cuadrado la raíz cúbica del volumen de la molécula:

a_{0}=V_{\text{molécula}}^{\frac {2}{3}}=\left({\frac {\bar {M}}{\rho N_{\text{A}}}}\right)^{\frac {2}{3}}

Aquí, $M̄$ corresponde a la masa molar de la molécula, $ρ$ corresponde a la densidad y $N A$ es la constante de Avogadro .

Para determinar la energía intermolecular por pares, se deben romper todas las fuerzas intermoleculares del material. Esto permite una investigación exhaustiva de las interacciones que se producen entre moléculas individuales. Durante la sublimación de una sustancia, las fuerzas intermoleculares entre las moléculas se rompen, lo que da como resultado un cambio en el material de sólido a gas. Por este motivo, puede resultar útil considerar la entalpía de sublimación para determinar la energía intermolecular por pares. La entalpía de sublimación se puede calcular mediante la siguiente ecuación:

\Delta _{\text{sub}}H=-{\frac {1}{2}}W_{\text{AA}}N_{\text{A}}z_{b}

Utilizando valores tabulados empíricamente para la entalpía de sublimación, es posible determinar la energía intermolecular por pares. Incorporando este valor en la ecuación de energía superficial, es posible estimar la energía superficial.

La siguiente ecuación se puede utilizar como una estimación razonable de la energía superficial:

\gamma \approx {\frac {-\Delta _{\text{sub}}H\left(z_{\sigma }-z_{\beta }\right)}{a_{0}N_{\text{A}}z_{\beta }}}

Energía interfacial

La presencia de una interfase influye de manera general en todos los parámetros termodinámicos de un sistema. Existen dos modelos que se utilizan habitualmente para demostrar los fenómenos interfaciales: el modelo de interfase ideal de Gibbs y el modelo de Guggenheim. Para demostrar la termodinámica de un sistema interfacial utilizando el modelo de Gibbs, el sistema se puede dividir en tres partes: dos líquidos inmiscibles con volúmenes $V α$ y $V β$ y una capa límite infinitesimalmente delgada conocida como plano divisor de Gibbs ( $σ$ ) que separa estos dos volúmenes.

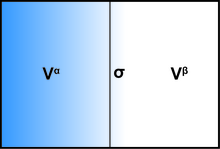
El volumen total del sistema es:

V=V_{\alpha }+V_{\beta }

Todas las cantidades extensivas del sistema pueden escribirse como una suma de tres componentes: fase volumétrica $α$ , fase volumétrica $β$ y la interfase $σ$ . Algunos ejemplos incluyen la energía interna $U$ , el número de moléculas de la $i$ ésima sustancia $n i$ y la entropía $S$ .

{\begin{aligned}U&=U_{\alpha}+U_{\beta}+U_{\sigma}\\N_{i}&=N_{i\alpha}+N_{i\beta}+N_{i\sigma}\\S&=S_{\alpha}+S_{\beta}+S_{\sigma}\end{aligned}}

Si bien estas cantidades pueden variar entre cada componente, la suma dentro del sistema permanece constante. En la interfase, estos valores pueden diferir de los presentes en las fases en masa. La concentración de moléculas presentes en la interfase se puede definir como:

N_{i\sigma}=N_{i}-c_{i\alpha}V_{\alpha}-c_{i\beta}V_{\beta}

donde $c iα$ y $c iβ$ representan la concentración de la sustancia $i$ en la fase masiva $α$ y $β$ , respectivamente.

Es conveniente definir un nuevo término, exceso interfacial $Γ i,$ que nos permita describir el número de moléculas por unidad de área:

\Gamma _{i}={\frac {N_{i\alpha }}{A}}

Mojada

Parámetro de propagación

La energía superficial entra en juego en los fenómenos de humectación. Para examinar esto, considere una gota de líquido sobre un sustrato sólido. Si la energía superficial del sustrato cambia al agregar la gota, se dice que el sustrato se está humectando . El parámetro de propagación se puede utilizar para determinar esto matemáticamente:

S=\gamma _{\text{s}}-\gamma _{\text{l}}-\gamma _{\text{sl}}

donde $S$ es el parámetro de expansión, $γ s$ la energía superficial del sustrato, $γ l$ la energía superficial del líquido y $γ s-l$ la energía interfacial entre el sustrato y el líquido.

Si $S < 0$ , el líquido humedece parcialmente el sustrato. Si $S > 0$ , el líquido humedece completamente el sustrato. ^[9]

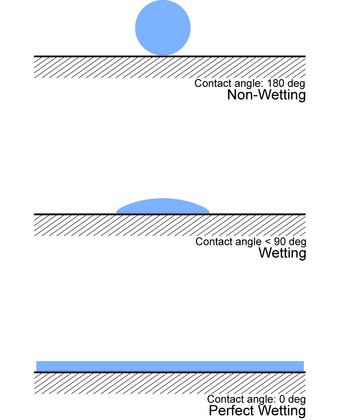
Ángulos de contacto: no humectante, humectante y humectante perfecto. El ángulo de contacto es el ángulo que conecta la interfaz sólido-líquido y la interfaz líquido-gas.

Angulo de contacto

Una forma de determinar experimentalmente la humectación es observar el ángulo de contacto ( $θ$ ), que es el ángulo que conecta la interfaz sólido-líquido y la interfaz líquido-gas (como en la figura).

Si

θ = 0°

, el líquido moja completamente el sustrato.

Si

0° < θ < 90°

, se produce una alta humectación.

Si

90° < θ < 180°

, se produce una humectación baja.

Si

θ = 180°

, el líquido no moja en absoluto el sustrato. ^[10]

La ecuación de Young relaciona el ángulo de contacto con la energía interfacial:

\gamma _{\text{sg}}=\gamma _{\text{sl}}+\gamma _{\text{lg}}\cos \theta

donde $γ s-g$ es la energía interfacial entre las fases sólida y gaseosa, $γ s-l$ la energía interfacial entre el sustrato y el líquido, $γ l-g$ es la energía interfacial entre las fases líquida y gaseosa, y $θ$ es el ángulo de contacto entre la interfaz sólido-líquido y líquido-gas. ^[11]

Humectación de sustratos de alta y baja energía.

La energía del componente principal de un sustrato sólido está determinada por los tipos de interacciones que mantienen unido al sustrato. Los sustratos de alta energía se mantienen unidos por enlaces , mientras que los sustratos de baja energía se mantienen unidos por fuerzas . Los enlaces covalentes , iónicos y metálicos son mucho más fuertes que fuerzas como los enlaces de van der Waals y los enlaces de hidrógeno . Los sustratos de alta energía se humedecen más fácilmente que los sustratos de baja energía. ^[12] Además, se producirá una humectación más completa si el sustrato tiene una energía superficial mucho mayor que el líquido. ^[13]

Técnicas de modificación

Los protocolos de modificación de superficies más utilizados son la activación por plasma , el tratamiento químico húmedo, incluido el injerto, y el recubrimiento de película fina. ^[14]^[15]^[16] La imitación de energía de superficie es una técnica que permite fusionar la fabricación del dispositivo y las modificaciones de la superficie, incluido el modelado, en un solo paso de procesamiento utilizando un solo material del dispositivo. ^[17]

Se pueden utilizar muchas técnicas para mejorar la humectación. Se pueden utilizar tratamientos de superficie, como el tratamiento corona , ^[18] el tratamiento con plasma y el grabado ácido , ^[19] para aumentar la energía superficial del sustrato. También se pueden añadir aditivos al líquido para disminuir su tensión superficial. Esta técnica se emplea a menudo en formulaciones de pintura para garantizar que se extiendan uniformemente sobre una superficie. ^[20]

La ecuación de Kelvin

Como resultado de la tensión superficial inherente a los líquidos, se forman superficies curvas con el fin de minimizar el área. Este fenómeno surge del costo energético de formar una superficie. Por lo tanto, la energía libre de Gibbs del sistema se minimiza cuando la superficie es curva.

La ecuación de Kelvin se basa en principios termodinámicos y se utiliza para describir los cambios en la presión de vapor provocados por líquidos con superficies curvas. La causa de este cambio en la presión de vapor es la presión de Laplace. La presión de vapor de una gota es mayor que la de una superficie plana porque el aumento de la presión de Laplace hace que las moléculas se evaporen más fácilmente. Por el contrario, en los líquidos que rodean una burbuja, la presión con respecto a la parte interna de la burbuja se reduce, lo que dificulta la evaporación de las moléculas. La ecuación de Kelvin se puede expresar como:

RT\ln {\frac {P_{0}^{K}}{P_{0}}}=\gamma V_{m}\left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)

donde $P K0 $ es la presión de vapor de la superficie curva, $P 0$ es la presión de vapor de la superficie plana, $γ$ es la tensión superficial , $V m$ es el volumen molar del líquido, $R$ es la constante universal de los gases , $T$ es la temperatura (en kelvin ), y $R 1$ y $R 2$ son los radios principales de curvatura de la superficie.

Pigmentos modificados superficialmente para recubrimientos

Los pigmentos ofrecen un gran potencial para modificar las propiedades de aplicación de un recubrimiento. Debido a su fino tamaño de partícula y a su inherentemente alta energía superficial, a menudo requieren un tratamiento de superficie para mejorar su facilidad de dispersión en un medio líquido. Anteriormente se ha utilizado una amplia variedad de tratamientos de superficie, incluida la adsorción en la superficie de una molécula en presencia de grupos polares, monocapas de polímeros y capas de óxidos inorgánicos en la superficie de pigmentos orgánicos. ^[21]

Constantemente se crean nuevas superficies a medida que partículas de pigmento más grandes se descomponen en subpartículas más pequeñas. Estas superficies recién formadas contribuyen en consecuencia a energías superficiales más grandes, por lo que las partículas resultantes a menudo se cementan juntas en agregados. Debido a que las partículas dispersas en medios líquidos están en constante movimiento térmico o browniano , exhiben una fuerte afinidad por otras partículas de pigmento cercanas a medida que se mueven a través del medio y chocan. ^{[21] Esta atracción natural se atribuye en gran medida a las poderosas}fuerzas de van der Waals de corto alcance , como un efecto de sus energías superficiales.

El objetivo principal de la dispersión de pigmentos es descomponer los agregados y formar dispersiones estables de partículas de pigmento de tamaño óptimo. Este proceso generalmente implica tres etapas distintas: humectación, desagregación y estabilización. Una superficie que sea fácil de humedecer es deseable cuando se formula un recubrimiento que requiere buena adhesión y apariencia. Esto también minimiza los riesgos de defectos relacionados con la tensión superficial, como el arrastre, la formación de cráteres y la piel de naranja . ^[22] Este es un requisito esencial para las dispersiones de pigmentos; para que la humectación sea efectiva, la tensión superficial del vehículo del pigmento debe ser menor que la energía libre superficial del pigmento. ^[21] Esto permite que el vehículo penetre en los intersticios de los agregados de pigmento, asegurando así una humectación completa. Finalmente, las partículas se someten a una fuerza repulsiva para mantenerlas separadas entre sí y reducir la probabilidad de floculación .

Las dispersiones pueden estabilizarse mediante dos fenómenos diferentes: repulsión de carga y repulsión estérica o entrópica. ^[22] En la repulsión de carga, las partículas que poseen las mismas cargas electrostáticas se repelen entre sí. Alternativamente, la repulsión estérica o entrópica es un fenómeno utilizado para describir el efecto repulsivo cuando las capas adsorbidas de material (como las moléculas de polímero hinchadas con disolvente) están presentes en la superficie de las partículas de pigmento en dispersión. Solo se adsorben ciertas porciones (anclajes) de las moléculas de polímero, con sus bucles y colas correspondientes extendiéndose hacia la solución. A medida que las partículas se aproximan entre sí, sus capas adsorbidas se apiñan; esto proporciona una barrera estérica eficaz que evita la floculación . ^[23] Este efecto de apiñamiento va acompañado de una disminución de la entropía, por lo que se reduce el número de conformaciones posibles para las moléculas de polímero en la capa adsorbida. Como resultado, la energía aumenta y a menudo da lugar a fuerzas repulsivas que ayudan a mantener las partículas separadas entre sí.

Energías superficiales de materiales comunes

Material	Orientación	Energía superficial (mJ/m ² )
Politetrafluoroetileno (PTFE)		19 ^[24]^{[ página necesaria ]}
Vaso		83.4 ^[25]
Yeso		370 ^[26]
Cobre		1650 ^[27]
Óxido de magnesio	(100) avión	1200 ^[28]
Fluoruro de calcio	(111) avión	450 ^[28]
Fluoruro de litio	(100) avión	340 ^[28]
Carbonato de calcio	(1010) avión	230 ^[28]
Cloruro de sodio	(100) avión	300 ^[29]
Cloruro de sodio	(110) avión	400 ^[30]
Cloruro de potasio	(100) avión	110 ^[29]
Fluoruro de bario	(111) avión	280 ^[28]
Silicio	(111) avión	1240 ^[28]

Véase también

Referencias

^ Marshall, SJ; Bayne, SC; Baier, R.; Tomsia, AP; Marshall, GW (2010). "Una revisión de la ciencia de la adhesión". Materiales dentales . 26 (2): e11–e16. doi :10.1016/j.dental.2009.11.157. PMID 20018362.
^ Laurén, S. "¿Cómo medir la energía libre superficial?". blog.biolinscientific.com . Biolin Scientific . Consultado el 31 de diciembre de 2019 .
^ "Energía libre superficial: mediciones". biolinscientific.com . Biolin Scientific . Consultado el 31 de diciembre de 2019 .
^ "ISO 19403-2:2017. Pinturas y barnices. Mojabilidad. Parte 2: Determinación de la energía libre superficial de superficies sólidas midiendo el ángulo de contacto". ISO . 2017.
^ Woodruff, DP, ed. (2002). La física química de superficies sólidas . Vol. 10. Elsevier.^{[ Falta ISBN ]}
^ Mecánica de contacto y fricción: principios físicos y aplicaciones . Springer. 2017. ISBN 9783662530801.
^ Popov, VL; Pohrt, R.; Li, Q. (septiembre de 2017). "Fuerza de los contactos adhesivos: influencia de la geometría de contacto y los gradientes del material". Fricción . 5 (3): 308–325. doi : 10.1007/s40544-017-0177-3 .
^ Departamento de Dinámica de Sistemas y Física de la Fricción (6 de diciembre de 2017). «Ciencia de la fricción: Adhesión de formas complejas». YouTube . Archivado desde el original el 2021-12-12 . Consultado el 2018-01-28 .
^ Bonn, D.; Eggers, J.; Indekeu, J.; Meunier, J.; Rolley, E. (2009). "Mojadura y propagación". Reseñas de Física Moderna . 81 (2): 739–805. Bibcode :2009RvMP...81..739B. doi :10.1103/revmodphys.81.739.
^ Zisman, W. (1964). "Relación del ángulo de contacto de equilibrio con la constitución líquida y sólida". Ángulo de contacto, mojabilidad y adhesión . Avances en química. Vol. 43. págs. 1–51. doi : 10.1021/ba-1964-0043.ch001 . ISBN. 0-8412-0044-0.
^ Owens, DK; Wendt, RC (1969). "Estimación de la energía libre superficial de polímeros". Revista de ciencia aplicada de polímeros . 13 (8): 1741–1747. doi :10.1002/app.1969.070130815.
^ De Gennes, PG (1985). "Mojadura: estática y dinámica". Reseñas de Física Moderna . 57 (3): 827–863. Bibcode :1985RvMP...57..827D. doi :10.1103/revmodphys.57.827.
^ Kern, K.; David, R.; Palmer, RL; Cosma, G. (1986). "Humedecimiento completo en sustratos 'fuertes': Xe/Pt(111)". Physical Review Letters . 56 (26): 2823–2826. Bibcode :1986PhRvL..56.2823K. doi :10.1103/physrevlett.56.2823. PMID 10033104.
^ Becker, H.; Gärtner, C. (2007). "Tecnologías de microfabricación de polímeros para sistemas microfluídicos". Química analítica y bioanalítica . 390 (1): 89–111. doi :10.1007/s00216-007-1692-2. PMID 17989961. S2CID 13813183.
^ Mansky (1997). "Control de interacciones polímero-superficie con cepillos de copolímeros aleatorios". Science . 275 (5305): 1458–1460. doi :10.1126/science.275.5305.1458. S2CID 136525970.
^ Rastogi (2010). "Modelado directo de cepillos de polímeros intrínsecamente sensibles al haz de electrones". ACS Nano . 4 (2): 771–780. doi :10.1021/nn901344u. PMID 20121228.
^ Pardon, G.; Haraldsson, T.; van der Wijngaart, W. (2016). "Imitación de energía superficial: replicación simultánea de micropatrones hidrófilos y superhidrófobos mediante autoensamblaje de monómeros selectivos de área". Advanced Materials Interfaces . 3 (17): 1600404. doi :10.1002/admi.201600404. S2CID 138114323.
^ Sakata, I.; Morita, M.; Tsuruta, N.; Morita, K. (2003). "Activación de la superficie de la madera mediante tratamiento Corona para mejorar la unión adhesiva". Journal of Applied Polymer Science . 49 (7): 1251–1258. doi :10.1002/app.1993.070490714.
^ Rosales, JI; Marshall, GW; Marshall, SJ; Wantanabe, LG; Toledano, M.; Cabrerizo, MA; Osorio, R. (1999). "Influencia del grabado ácido y la hidratación en la rugosidad y humectabilidad de la dentina". Journal of Dental Research . 78 (9): 1554–1559. doi :10.1177/00220345990780091001. PMID 10512390. S2CID 5807073.
^ Khan, H.; Fell, JT; Macleod, GS (2001). "La influencia de los aditivos en el coeficiente de dispersión y la adhesión de una formulación de recubrimiento de película a la superficie de un comprimido modelo". Revista internacional de farmacia . 227 (1–2): 113–119. doi :10.1016/s0378-5173(01)00789-x. PMID 11564545.
^ abc Wicks, ZW (2007). Recubrimientos orgánicos: ciencia y tecnología (3.ª ed.). Nueva York: Wiley Interscience. págs. 435–441.^{[ Falta ISBN ]}
^ ab Tracton, AA (2006). Materiales de recubrimiento y recubrimientos de superficies (3.ª ed.). Florida: Taylor and Francis Group. págs. 31-6–31-7.^{[ Falta ISBN ]}
^ Auschra, C.; Eckstein, E.; Muhlebach, A.; Zink, M.; Rime, F. (2002). "Diseño de nuevos dispersantes de pigmentos mediante polimerización radical controlada". Progress in Organic Coatings . 45 (2–3): 83–93. doi :10.1016/s0300-9440(02)00048-6.
^ Kinloch, AJ (1987). Adhesión y adhesivos: ciencia y tecnología . Londres: Chapman & Hall.^{[ Falta ISBN ]}
^ Rhee, S.-K. (1977). "Energías superficiales de vidrios de silicato calculadas a partir de sus datos de mojabilidad". Revista de Ciencia de Materiales . 12 (4): 823–824. Código Bibliográfico :1977JMatS..12..823R. doi :10.1007/BF00548176. S2CID 136812418.
^ Dundon, ML; Mack, E. (1923). "La solubilidad y la energía superficial del sulfato de calcio". Revista de la Sociedad Química Americana . 45 (11): 2479–2485. doi :10.1021/ja01664a001.
^ Udin, H. (1951). "Efecto del límite de grano en la medición de la tensión superficial". JOM . 3 (1): 63. Bibcode :1951JOM.....3a..63U. doi : 10.1007/BF03398958 .
^ abcdef Gilman, JJ (1960). "Medidas directas de las energías superficiales de los cristales". Journal of Applied Physics . 31 (12): 2208. Bibcode :1960JAP....31.2208G. doi :10.1063/1.1735524.
^ ab Butt, H.-J.; Graf, Kh.; Kappl, M. (2006). Física y química de interfaces . Weinheim: Wiley-VCH.^{[ Falta ISBN ]}
^ Lipsett, SG; Johnson, FMG; Maass, O. (1927). "La energía superficial y el calor de solución de cloruro de sodio sólido. I". Revista de la Sociedad Química Americana . 49 (4): 925. doi :10.1021/ja01403a005.

Enlaces externos

¿Qué es la energía libre superficial?
Energía superficial y adhesión

[1] Marshall, SJ; Bayne, SC; Baier, R.; Tomsia, AP; Marshall, GW (2010). "Una revisión de la ciencia de la adhesión". Materiales dentales . 26 (2): e11–e16. doi :10.1016/j.dental.2009.11.157. PMID 20018362.

[2] Laurén, S. "¿Cómo medir la energía libre superficial?". blog.biolinscientific.com . Biolin Scientific . Consultado el 31 de diciembre de 2019 .

[3] "Energía libre superficial: mediciones". biolinscientific.com . Biolin Scientific . Consultado el 31 de diciembre de 2019 .

[4] "ISO 19403-2:2017. Pinturas y barnices. Mojabilidad. Parte 2: Determinación de la energía libre superficial de superficies sólidas midiendo el ángulo de contacto". ISO . 2017.

[5] Woodruff, DP, ed. (2002). La física química de superficies sólidas . Vol. 10. Elsevier.^{[ Falta ISBN ]}

[6] Mecánica de contacto y fricción: principios físicos y aplicaciones . Springer. 2017. ISBN 9783662530801.

[7] Popov, VL; Pohrt, R.; Li, Q. (septiembre de 2017). "Fuerza de los contactos adhesivos: influencia de la geometría de contacto y los gradientes del material". Fricción . 5 (3): 308–325. doi : 10.1007/s40544-017-0177-3 .

[8] Departamento de Dinámica de Sistemas y Física de la Fricción (6 de diciembre de 2017). «Ciencia de la fricción: Adhesión de formas complejas». YouTube . Archivado desde el original el 2021-12-12 . Consultado el 2018-01-28 .

[9] Bonn, D.; Eggers, J.; Indekeu, J.; Meunier, J.; Rolley, E. (2009). "Mojadura y propagación". Reseñas de Física Moderna . 81 (2): 739–805. Bibcode :2009RvMP...81..739B. doi :10.1103/revmodphys.81.739.

[10] Zisman, W. (1964). "Relación del ángulo de contacto de equilibrio con la constitución líquida y sólida". Ángulo de contacto, mojabilidad y adhesión . Avances en química. Vol. 43. págs. 1–51. doi : 10.1021/ba-1964-0043.ch001 . ISBN. 0-8412-0044-0.

[11] Owens, DK; Wendt, RC (1969). "Estimación de la energía libre superficial de polímeros". Revista de ciencia aplicada de polímeros . 13 (8): 1741–1747. doi :10.1002/app.1969.070130815.

[12] De Gennes, PG (1985). "Mojadura: estática y dinámica". Reseñas de Física Moderna . 57 (3): 827–863. Bibcode :1985RvMP...57..827D. doi :10.1103/revmodphys.57.827.

[13] Kern, K.; David, R.; Palmer, RL; Cosma, G. (1986). "Humedecimiento completo en sustratos 'fuertes': Xe/Pt(111)". Physical Review Letters . 56 (26): 2823–2826. Bibcode :1986PhRvL..56.2823K. doi :10.1103/physrevlett.56.2823. PMID 10033104.

[14] Becker, H.; Gärtner, C. (2007). "Tecnologías de microfabricación de polímeros para sistemas microfluídicos". Química analítica y bioanalítica . 390 (1): 89–111. doi :10.1007/s00216-007-1692-2. PMID 17989961. S2CID 13813183.

[15] Mansky (1997). "Control de interacciones polímero-superficie con cepillos de copolímeros aleatorios". Science . 275 (5305): 1458–1460. doi :10.1126/science.275.5305.1458. S2CID 136525970.

[16] Rastogi (2010). "Modelado directo de cepillos de polímeros intrínsecamente sensibles al haz de electrones". ACS Nano . 4 (2): 771–780. doi :10.1021/nn901344u. PMID 20121228.

[17] Pardon, G.; Haraldsson, T.; van der Wijngaart, W. (2016). "Imitación de energía superficial: replicación simultánea de micropatrones hidrófilos y superhidrófobos mediante autoensamblaje de monómeros selectivos de área". Advanced Materials Interfaces . 3 (17): 1600404. doi :10.1002/admi.201600404. S2CID 138114323.

[18] Sakata, I.; Morita, M.; Tsuruta, N.; Morita, K. (2003). "Activación de la superficie de la madera mediante tratamiento Corona para mejorar la unión adhesiva". Journal of Applied Polymer Science . 49 (7): 1251–1258. doi :10.1002/app.1993.070490714.

[19] Rosales, JI; Marshall, GW; Marshall, SJ; Wantanabe, LG; Toledano, M.; Cabrerizo, MA; Osorio, R. (1999). "Influencia del grabado ácido y la hidratación en la rugosidad y humectabilidad de la dentina". Journal of Dental Research . 78 (9): 1554–1559. doi :10.1177/00220345990780091001. PMID 10512390. S2CID 5807073.

[20] Khan, H.; Fell, JT; Macleod, GS (2001). "La influencia de los aditivos en el coeficiente de dispersión y la adhesión de una formulación de recubrimiento de película a la superficie de un comprimido modelo". Revista internacional de farmacia . 227 (1–2): 113–119. doi :10.1016/s0378-5173(01)00789-x. PMID 11564545.

[Wicks,_Z.W._2007-21] Wicks, ZW (2007). Recubrimientos orgánicos: ciencia y tecnología (3.ª ed.). Nueva York: Wiley Interscience. págs. 435–441.^{[ Falta ISBN ]}

[Tracton,_A._A._2006-22] Tracton, AA (2006). Materiales de recubrimiento y recubrimientos de superficies (3.ª ed.). Florida: Taylor and Francis Group. págs. 31-6–31-7.^{[ Falta ISBN ]}

[23] Auschra, C.; Eckstein, E.; Muhlebach, A.; Zink, M.; Rime, F. (2002). "Diseño de nuevos dispersantes de pigmentos mediante polimerización radical controlada". Progress in Organic Coatings . 45 (2–3): 83–93. doi :10.1016/s0300-9440(02)00048-6.

[24] Kinloch, AJ (1987). Adhesión y adhesivos: ciencia y tecnología . Londres: Chapman & Hall.^{[ Falta ISBN ]}

[25] Rhee, S.-K. (1977). "Energías superficiales de vidrios de silicato calculadas a partir de sus datos de mojabilidad". Revista de Ciencia de Materiales . 12 (4): 823–824. Código Bibliográfico :1977JMatS..12..823R. doi :10.1007/BF00548176. S2CID 136812418.

[26] Dundon, ML; Mack, E. (1923). "La solubilidad y la energía superficial del sulfato de calcio". Revista de la Sociedad Química Americana . 45 (11): 2479–2485. doi :10.1021/ja01664a001.

[27] Udin, H. (1951). "Efecto del límite de grano en la medición de la tensión superficial". JOM . 3 (1): 63. Bibcode :1951JOM.....3a..63U. doi : 10.1007/BF03398958 .

[Gilman,_J._J._1960-28] Gilman, JJ (1960). "Medidas directas de las energías superficiales de los cristales". Journal of Applied Physics . 31 (12): 2208. Bibcode :1960JAP....31.2208G. doi :10.1063/1.1735524.

[Butt,_Hans-Jürgen_2006-29] Butt, H.-J.; Graf, Kh.; Kappl, M. (2006). Física y química de interfaces . Weinheim: Wiley-VCH.^{[ Falta ISBN ]}

[30] Lipsett, SG; Johnson, FMG; Maass, O. (1927). "La energía superficial y el calor de solución de cloruro de sodio sólido. I". Revista de la Sociedad Química Americana . 49 (4): 925. doi :10.1021/ja01403a005.