Leyes de De Morgan

En lógica proposicional y álgebra de Boole , las leyes de De Morgan , ^{[1] [2] [3]} también conocidas como teorema de De Morgan , ^[4] son ​​un par de reglas de transformación que son reglas de inferencia válidas . Reciben su nombre de Augustus De Morgan , un matemático británico del siglo XIX. Las reglas permiten la expresión de conjunciones y disyunciones puramente en términos entre sí a través de la negación .

Las reglas se pueden expresar en inglés como:

• La negación de "A y B" es lo mismo que "no A o no B".
• La negación de "A o B" es lo mismo que "no A y no B".

o

• El complemento de la unión de dos conjuntos es el mismo que la intersección de sus complementos
• El complemento de la intersección de dos conjuntos es el mismo que la unión de sus complementos

o

• no (A o B) = (no A) y (no B)
• no (A y B) = (no A) o (no B)

donde "A o B" es un " o inclusivo " que significa al menos uno de A o B en lugar de un " o exclusivo " que significa exactamente uno de A o B.

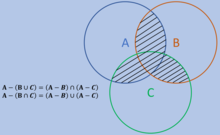
Otra forma de la ley de De Morgan es la siguiente, como se ve a continuación.

${\displaystyle A-(B\cup C)=(A-B)\cap (A-C),}$

${\displaystyle A-(B\cap C)=(A-B)\cup (A-C).}$

Las aplicaciones de las reglas incluyen la simplificación de expresiones lógicas en programas informáticos y diseños de circuitos digitales. Las leyes de De Morgan son un ejemplo de un concepto más general de dualidad matemática .

La regla de negación de la conjunción puede escribirse en notación secuencial :

${\displaystyle {\begin{aligned}\neg (P\land Q)&\vdash (\neg P\lor \neg Q),{\text{and}}\\(\neg P\lor \neg Q)&\vdash \neg (P\land Q).\end{aligned}}}$

La regla de negación de la disyunción puede escribirse como:

${\displaystyle {\begin{aligned}\neg (P\lor Q)&\vdash (\neg P\land \neg Q),{\text{and}}\\(\neg P\land \neg Q)&\vdash \neg (P\lor Q).\end{aligned}}}$

En forma de regla : negación de la conjunción

y negación de la disyunción

y expresados ​​como tautologías veritativo-funcionales o teoremas de lógica proposicional:

${\displaystyle {\begin{aligned}\neg (P\land Q)&\leftrightarrow (\neg P\lor \neg Q),\\\neg (P\lor Q)&\leftrightarrow (\neg P\land \neg Q).\\\end{aligned}}}$

donde y son proposiciones expresadas en algún sistema formal.${\displaystyle P}$${\displaystyle Q}$

Las leyes de De Morgan generalizadas proporcionan una equivalencia para negar una conjunción o disyunción que involucra múltiples términos.
Para un conjunto de proposiciones , las leyes de De Morgan generalizadas son las siguientes:${\displaystyle P_{1},P_{2},\dots ,P_{n}}$

${\displaystyle {\begin{aligned}\lnot (P_{1}\land P_{2}\land \dots \land P_{n})\leftrightarrow \lnot P_{1}\lor \lnot P_{2}\lor \ldots \lor \lnot P_{n}\\\lnot (P_{1}\lor P_{2}\lor \dots \lor P_{n})\leftrightarrow \lnot P_{1}\land \lnot P_{2}\land \ldots \land \lnot P_{n}\end{aligned}}}$

Estas leyes generalizan las leyes originales de De Morgan para negar conjunciones y disyunciones.

Las leyes de De Morgan se muestran normalmente en la forma compacta que se muestra arriba, con la negación de la salida a la izquierda y la negación de las entradas a la derecha. Una forma más clara de la sustitución se puede expresar de la siguiente manera:

${\displaystyle {\begin{aligned}(P\land Q)&\Longleftrightarrow \neg (\neg P\lor \neg Q),\\(P\lor Q)&\Longleftrightarrow \neg (\neg P\land \neg Q).\end{aligned}}}$

Esto enfatiza la necesidad de invertir tanto las entradas como la salida, así como cambiar el operador cuando se realiza una sustitución.

En la teoría de conjuntos, a menudo se expresa como "unión e intersección intercambiadas bajo complementación", ^[5] lo que se puede expresar formalmente como:

${\displaystyle {\begin{aligned}{\overline {A\cup B}}&={\overline {A}}\cap {\overline {B}},\\{\overline {A\cap B}}&={\overline {A}}\cup {\overline {B}},\end{aligned}}}$

dónde:

• ${\displaystyle {\overline {A}}}$es la negación de , escribiéndose la línea superior encima de los términos que se van a negar,${\displaystyle A}$
• ${\displaystyle \cap }$es el operador de intersección (AND),
• ${\displaystyle \cup }$es el operador de unión (OR).

La forma generalizada es

${\displaystyle {\begin{aligned}{\overline {\bigcap _{i\in I}A_{i}}}&\equiv \bigcup _{i\in I}{\overline {A_{i}}},\\{\overline {\bigcup _{i\in I}A_{i}}}&\equiv \bigcap _{i\in I}{\overline {A_{i}}},\end{aligned}}}$

donde I es un conjunto de indexación posiblemente infinito, numerable o incontable.

En notación de conjuntos, las leyes de De Morgan pueden recordarse utilizando la regla mnemotécnica "romper la línea, cambiar el signo". ^[6]

De manera similar, en el álgebra de Boole, esta ley puede expresarse formalmente como:

${\displaystyle {\begin{aligned}{\overline {A\land B}}&={\overline {A}}\lor {\overline {B}},\\{\overline {A\lor B}}&={\overline {A}}\land {\overline {B}},\end{aligned}}}$

dónde:

• ${\displaystyle {\overline {A}}}$es la negación de , escribiéndose la línea superior encima de los términos que se van a negar,${\displaystyle A}$
• ${\displaystyle \land }$es el operador de conjunción lógica (AND),
• ${\displaystyle \lor }$es el operador de disyunción lógica (OR).

que puede generalizarse a

${\displaystyle {\begin{aligned}{\overline {A_{1}\land A_{2}\land \ldots \land A_{n}}}={\overline {A_{1}}}\lor {\overline {A_{2}}}\lor \ldots \lor {\overline {A_{n}}},\\{\overline {A_{1}\lor A_{2}\lor \ldots \lor A_{n}}}={\overline {A_{1}}}\land {\overline {A_{2}}}\land \ldots \land {\overline {A_{n}}}.\end{aligned}}}$

En ingeniería eléctrica e informática , las leyes de De Morgan se escriben comúnmente como:

${\displaystyle {\overline {(A\cdot B)}}\equiv ({\overline {A}}+{\overline {B}})}$

y

${\displaystyle {\overline {(A+B)}}\equiv ({\overline {A}}\cdot {\overline {B}}),}$

dónde:

• ${\displaystyle \cdot }$es el AND lógico,
• ${\displaystyle +}$es el OR lógico,
• La barra superior es el NO lógico de lo que está debajo de la barra superior.

Las leyes de De Morgan se aplican comúnmente a la búsqueda de texto mediante los operadores booleanos AND, OR y NOT. Considere un conjunto de documentos que contengan las palabras "gatos" y "perros". Las leyes de De Morgan sostienen que estas dos búsquedas devolverán el mismo conjunto de documentos:

Buscar A: NO (gatos O perros)

Búsqueda B: (NO gatos) Y (NO perros)

El corpus de documentos que contiene "gatos" o "perros" puede estar representado por cuatro documentos:

Documento 1: Contiene sólo la palabra "gatos".

Documento 2: Contiene únicamente "perros".

Documento 3: Contiene tanto "gatos" como "perros".

Documento 4: No contiene ni "gatos" ni "perros".

Para evaluar la Búsqueda A, claramente la búsqueda "(gatos O perros)" afectará a los Documentos 1, 2 y 3. Por lo tanto, la negación de esa búsqueda (que es la Búsqueda A) afectará a todo lo demás, que es el Documento 4.

Al evaluar la Búsqueda B, la búsqueda "(NO gatos)" dará como resultado documentos que no contengan "gatos", es decir, los Documentos 2 y 4. De manera similar, la búsqueda "(NO perros)" dará como resultado los Documentos 1 y 4. Al aplicar el operador AND a estas dos búsquedas (que es la Búsqueda B), dará como resultado los documentos que son comunes a estas dos búsquedas, es decir, el Documento 4.

Se puede aplicar una evaluación similar para demostrar que las dos búsquedas siguientes devolverán los Documentos 1, 2 y 4:

Buscar C:NO (gatos Y perros),

Buscar D: (NO gatos) O (NO perros).

Las leyes reciben su nombre de Augustus De Morgan (1806-1871), ^[7] quien introdujo una versión formal de las leyes en la lógica proposicional clásica . La formulación de De Morgan estuvo influenciada por la algebrización de la lógica realizada por George Boole , que más tarde consolidó la afirmación de De Morgan sobre el hallazgo. Sin embargo, Aristóteles hizo una observación similar , que era conocida por los lógicos griegos y medievales. ^[8] Por ejemplo, en el siglo XIV, Guillermo de Ockham escribió las palabras que resultarían de la lectura de las leyes. ^[9] Jean Buridan , en su Summulae de Dialectica , también describe reglas de conversión que siguen las líneas de las leyes de De Morgan. ^[10] Aun así, a De Morgan se le atribuye el mérito de enunciar las leyes en términos de la lógica formal moderna e incorporarlas al lenguaje de la lógica. Las leyes de De Morgan se pueden demostrar fácilmente e incluso pueden parecer triviales. ^[11] No obstante, estas leyes son útiles para hacer inferencias válidas en pruebas y argumentos deductivos.

El teorema de De Morgan puede aplicarse a la negación de una disyunción o a la negación de una conjunción en todo o parte de una fórmula.

En el caso de su aplicación a una disyunción, considérese la siguiente afirmación: "es falso que A o B sea verdadero", que se escribe así:

${\displaystyle \neg (A\lor B).}$

Como se ha establecido que ni A ni B son verdaderos, entonces debe seguirse que tanto A como B no son verdaderos, lo que puede escribirse directamente como:

${\displaystyle (\neg A)\wedge (\neg B).}$

Si A o B fueran verdaderas, entonces la disyunción de A y B sería verdadera, lo que haría falsa su negación. En inglés, esto sigue la lógica de que "dado que dos cosas son falsas, también es falso que cualquiera de ellas sea verdadera".

En sentido inverso, la segunda expresión afirma que A es falso y B es falso (o, equivalentemente, que "no A" y "no B" son verdaderos). Sabiendo esto, una disyunción de A y B también debe ser falsa. La negación de dicha disyunción debe ser, por tanto, verdadera, y el resultado es idéntico a la primera afirmación.

La aplicación del teorema de De Morgan a una conjunción es muy similar a su aplicación a una disyunción, tanto en su forma como en su fundamento. Consideremos la siguiente afirmación: "es falso que A y B sean ambas verdaderas", que se escribe así:

${\displaystyle \neg (A\land B).}$

Para que esta afirmación sea verdadera, A o B, o ambas, deben ser falsas, porque si ambas fueran verdaderas, entonces la conjunción de A y B sería verdadera, haciendo falsa su negación. Por lo tanto, una (al menos) o más de A y B deben ser falsas (o equivalentemente, una o más de "no A" y "no B" deben ser verdaderas). Esto puede escribirse directamente como:

${\displaystyle (\neg A)\lor (\neg B).}$

Presentado en inglés, esto sigue la lógica de que "dado que es falso que dos cosas sean verdaderas, al menos una de ellas debe ser falsa".

Trabajando nuevamente en la dirección opuesta, la segunda expresión afirma que al menos una de las afirmaciones "no A" y "no B" debe ser verdadera, o equivalentemente, que al menos una de las afirmaciones "no A" y "no B" debe ser falsa. Como al menos una de ellas debe ser falsa, entonces su conjunción también sería falsa. La negación de dicha conjunción da como resultado una expresión verdadera, y esta expresión es idéntica a la primera afirmación.

Aquí usamos para denotar el complemento de A, como en el § Teoría de conjuntos y álgebra de Boole. La prueba se completa en 2 pasos demostrando tanto y .${\displaystyle {\overline {A}}}$${\displaystyle {\overline {A\cap B}}={\overline {A}}\cup {\overline {B}}}$${\displaystyle {\overline {A\cap B}}\subseteq {\overline {A}}\cup {\overline {B}}}$${\displaystyle {\overline {A}}\cup {\overline {B}}\subseteq {\overline {A\cap B}}}$

Sea . Entonces, .${\displaystyle x\in {\overline {A\cap B}}}$${\displaystyle x\not \in A\cap B}$

Porque , debe ser el caso que o .${\displaystyle A\cap B=\{\,y\ |\ y\in A\wedge y\in B\,\}}$${\displaystyle x\not \in A}$${\displaystyle x\not \in B}$

Si , entonces , entonces .${\displaystyle x\not \in A}$${\displaystyle x\in {\overline {A}}}$${\displaystyle x\in {\overline {A}}\cup {\overline {B}}}$

De manera similar, si , entonces , por lo tanto .${\displaystyle x\not \in B}$${\displaystyle x\in {\overline {B}}}$${\displaystyle x\in {\overline {A}}\cup {\overline {B}}}$

De este modo, ;${\displaystyle \forall x{\Big (}x\in {\overline {A\cap B}}\implies x\in {\overline {A}}\cup {\overline {B}}{\Big )}}$

eso es, .${\displaystyle {\overline {A\cap B}}\subseteq {\overline {A}}\cup {\overline {B}}}$

Para demostrar la dirección inversa, sea , y por contradicción supongamos .${\displaystyle x\in {\overline {A}}\cup {\overline {B}}}$${\displaystyle x\not \in {\overline {A\cap B}}}$

Bajo ese supuesto, debe ser el caso que ,${\displaystyle x\in A\cap B}$

por lo tanto se sigue que y , y por lo tanto y .${\displaystyle x\in A}$${\displaystyle x\in B}$${\displaystyle x\not \in {\overline {A}}}$${\displaystyle x\not \in {\overline {B}}}$

Sin embargo, eso significa , en contradicción con la hipótesis de que ,${\displaystyle x\not \in {\overline {A}}\cup {\overline {B}}}$${\displaystyle x\in {\overline {A}}\cup {\overline {B}}}$

Por lo tanto, la suposición no debe ser el caso, lo que significa que .${\displaystyle x\not \in {\overline {A\cap B}}}$${\displaystyle x\in {\overline {A\cap B}}}$

Por eso, ,${\displaystyle \forall x{\Big (}x\in {\overline {A}}\cup {\overline {B}}\implies x\in {\overline {A\cap B}}{\Big )}}$

eso es, .${\displaystyle {\overline {A}}\cup {\overline {B}}\subseteq {\overline {A\cap B}}}$

Si y , entonces ; esto concluye la prueba de la ley de De Morgan.${\displaystyle {\overline {A}}\cup {\overline {B}}\subseteq {\overline {A\cap B}}}$ ${\displaystyle {\overline {A\cap B}}\subseteq {\overline {A}}\cup {\overline {B}}}$${\displaystyle {\overline {A\cap B}}={\overline {A}}\cup {\overline {B}}}$

La otra ley de De Morgan, , se demuestra de manera similar.${\displaystyle {\overline {A\cup B}}={\overline {A}}\cap {\overline {B}}}$

En las extensiones de la lógica proposicional clásica, la dualidad todavía se mantiene (es decir, para cualquier operador lógico siempre se puede encontrar su dual), ya que en presencia de las identidades que gobiernan la negación, siempre se puede introducir un operador que sea el dual de De Morgan de otro. Esto conduce a una propiedad importante de las lógicas basadas en la lógica clásica , a saber, la existencia de formas normales de negación : cualquier fórmula es equivalente a otra fórmula donde las negaciones solo ocurren aplicadas a los átomos no lógicos de la fórmula. La existencia de formas normales de negación impulsa muchas aplicaciones, por ejemplo en el diseño de circuitos digitales , donde se utiliza para manipular los tipos de puertas lógicas , y en lógica formal, donde se necesita para encontrar la forma normal conjuntiva y la forma normal disyuntiva de una fórmula. Los programadores de computadoras las utilizan para simplificar o negar adecuadamente condiciones lógicas complicadas . También suelen ser útiles en cálculos en teoría de probabilidad elemental .

Definamos el dual de cualquier operador proposicional P( p , q , ...) en función de las proposiciones elementales p , q , ... como el operador definido por${\displaystyle {\mbox{P}}^{d}}$

${\displaystyle {\mbox{P}}^{d}(p,q,...)=\neg P(\neg p,\neg q,\dots ).}$

Esta dualidad se puede generalizar a los cuantificadores, así, por ejemplo, el cuantificador universal y el cuantificador existencial son duales:

${\displaystyle \forall x\,P(x)\equiv \neg [\exists x\,\neg P(x)]}$

${\displaystyle \exists x\,P(x)\equiv \neg [\forall x\,\neg P(x)]}$

Para relacionar estas dualidades cuantificadoras con las leyes de De Morgan, configure un modelo con un pequeño número de elementos en su dominio D , tal como

D = { a , b , c }.

Entonces

${\displaystyle \forall x\,P(x)\equiv P(a)\land P(b)\land P(c)}$

y

${\displaystyle \exists x\,P(x)\equiv P(a)\lor P(b)\lor P(c).}$

Pero, utilizando las leyes de De Morgan,

${\displaystyle P(a)\land P(b)\land P(c)\equiv \neg (\neg P(a)\lor \neg P(b)\lor \neg P(c))}$

y

${\displaystyle P(a)\lor P(b)\lor P(c)\equiv \neg (\neg P(a)\land \neg P(b)\land \neg P(c)),}$

verificando las dualidades cuantificadoras en el modelo.

Luego, las dualidades cuantificadoras pueden extenderse aún más a la lógica modal , relacionando los operadores de caja ("necesariamente") y diamante ("posiblemente"):

${\displaystyle \Box p\equiv \neg \Diamond \neg p,}$

${\displaystyle \Diamond p\equiv \neg \Box \neg p.}$

En su aplicación a las modalidades aléticas de posibilidad y necesidad, Aristóteles observó este caso, y en el caso de la lógica modal normal , la relación de estos operadores modales con la cuantificación se puede entender estableciendo modelos que utilicen la semántica de Kripke .

Tres de las cuatro implicaciones de las leyes de De Morgan se cumplen en la lógica intuicionista . En concreto, tenemos

${\displaystyle \neg (P\lor Q)\,\leftrightarrow \,{\big (}(\neg P)\land (\neg Q){\big )},}$

y

${\displaystyle {\big (}(\neg P)\lor (\neg Q){\big )}\,\to \,\neg (P\land Q).}$

El recíproco de la última implicación no se cumple en la lógica intuicionista pura. Es decir, el fracaso de la proposición conjunta no puede resolverse necesariamente como el fracaso de cualquiera de los dos conjuntos . Por ejemplo, de saber que no es el caso de que tanto Alice como Bob se presentaron a su cita, no se sigue quién no se presentó. El último principio es equivalente al principio del tercio débil excluido .${\displaystyle P\land Q}$ ${\displaystyle {\mathrm {WPEM} }}$

${\displaystyle (\neg P)\lor \neg (\neg P).}$

Esta forma débil puede utilizarse como base para una lógica intermedia . Para una versión refinada de la ley fallida relativa a los enunciados existenciales, véase el principio de omnisciencia menos limitado , que sin embargo es diferente de .${\displaystyle {\mathrm {LLPO} }}$${\displaystyle {\mathrm {WLPO} }}$

La validez de las otras tres leyes de De Morgan sigue siendo cierta si la negación se reemplaza por la implicación para algún predicado constante arbitrario C, lo que significa que las leyes anteriores siguen siendo verdaderas en la lógica minimal .${\displaystyle \neg P}$${\displaystyle P\to C}$

De manera similar a lo anterior, las leyes cuantificadoras:

${\displaystyle \forall x\,\neg P(x)\,\leftrightarrow \,\neg \exists x\,P(x)}$

y

${\displaystyle \exists x\,\neg P(x)\,\to \,\neg \forall x\,P(x).}$

son tautologías incluso en la lógica mínima con la negación reemplazada por una implicación de un fijo , mientras que el recíproco de la última ley no tiene por qué ser cierto en general.${\displaystyle Q}$

Además, todavía queda

${\displaystyle (P\lor Q)\,\to \,\neg {\big (}(\neg P)\land (\neg Q){\big )},}$

${\displaystyle (P\land Q)\,\to \,\neg {\big (}(\neg P)\lor (\neg Q){\big )},}$

${\displaystyle \forall x\,P(x)\,\to \,\neg \exists x\,\neg P(x),}$

${\displaystyle \exists x\,P(x)\,\to \,\neg \forall x\,\neg P(x),}$

pero su inversión implica exclusión del medio .${\displaystyle {\mathrm {PEM} }}$

• Las leyes de De Morgan se utilizan ampliamente en ingeniería informática y lógica digital con el propósito de simplificar diseños de circuitos. ^[12]
• En los lenguajes de programación modernos, debido a la optimización de compiladores e intérpretes, las diferencias de rendimiento entre estas opciones son insignificantes o completamente inexistentes.

• Dualidad conjunción/disyunción
• Homogeneidad (lingüística)
• Isomorfismo
• Lista de temas de álgebra de Boole
• Lista de identidades y relaciones de conjuntos
• Lógica positiva
• Álgebra de Morgan

• "Principio de dualidad", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Leyes de Morgan". MundoMatemático .
• Leyes de De Morgan en PlanetMath .
• Dualidad en la lógica y el lenguaje, Enciclopedia de Filosofía en Internet .