Difracción de rayos X

La difracción de rayos X es un término genérico para los fenómenos asociados con los cambios en la dirección de los rayos X debido a las interacciones con los electrones alrededor de los átomos. Se produce debido a la dispersión elástica , cuando no hay cambios en la energía de las ondas. El mapa resultante de las direcciones de los rayos X lejos de la muestra se llama patrón de difracción. Es diferente de la cristalografía de rayos X , que explota la difracción de rayos X para determinar la disposición de los átomos en los materiales, y también tiene otros componentes, como formas de mapear las mediciones de difracción experimentales a las posiciones de los átomos.

Este artículo ofrece una descripción general de la difracción de rayos X, comenzando con la historia temprana de los rayos X y el descubrimiento de que tienen los espaciamientos correctos para ser difractados por cristales. En muchos casos, estos patrones de difracción se pueden interpretar utilizando una sola teoría de dispersión o cinemática con conservación de energía (vector de onda). Existen muchos tipos diferentes de fuentes de rayos X, que van desde las que se utilizan en laboratorios hasta fuentes de luz de sincrotrón de mayor brillo . Se pueden producir patrones de difracción similares mediante técnicas de dispersión relacionadas, como la difracción de electrones o la difracción de neutrones . Si no se pueden obtener cristales individuales de tamaño suficiente, se pueden aplicar otros métodos de rayos X para obtener información menos detallada; dichos métodos incluyen difracción de fibra , difracción de polvo y (si la muestra no está cristalizada) dispersión de rayos X de ángulo pequeño (SAXS).

Cuando Wilhelm Röntgen descubrió los rayos X en 1895 ^[1] los físicos no estaban seguros de la naturaleza de los rayos X, pero sospechaban que eran ondas de radiación electromagnética . La teoría de Maxwell de la radiación electromagnética fue bien aceptada, y los experimentos de Charles Glover Barkla mostraron que los rayos X exhibían fenómenos asociados con las ondas electromagnéticas, incluyendo polarización transversal y líneas espectrales similares a las observadas en las longitudes de onda visibles. Barkla creó la notación de rayos X para las líneas espectrales agudas, notando en 1909 dos energías separadas, al principio, nombrándolas "A" y "B" y, suponiendo que puede haber líneas anteriores a "A", comenzó una numeración alfabética que comienza con "K". ^{[2] [3]} Los experimentos de una sola rendija en el laboratorio de Arnold Sommerfeld sugirieron que los rayos X tenían una longitud de onda de aproximadamente 1 angstrom . ^[4] Los rayos X no son sólo ondas, sino que también tienen propiedades de partículas, lo que provocó que Sommerfeld acuñara el nombre de Bremsstrahlung para los espectros continuos cuando se formaban cuando los electrones bombardeaban un material. ^[3] Albert Einstein introdujo el concepto de fotón en 1905, ^[5] pero no fue ampliamente aceptado hasta 1922, ^{[6] [7]} cuando Arthur Compton lo confirmó mediante la dispersión de rayos X de los electrones. ^[8] Las propiedades similares a partículas de los rayos X, como su ionización de los gases, habían llevado a William Henry Bragg a argumentar en 1907 que los rayos X no eran radiación electromagnética. ^{[9] [10] [11] [12]} La opinión de Bragg resultó impopular y la observación de la difracción de rayos X por Max von Laue en 1912 ^[13] confirmó que los rayos X son una forma de radiación electromagnética.

La idea de que los cristales podrían usarse como una rejilla de difracción para rayos X surgió en 1912 en una conversación entre Paul Peter Ewald y Max von Laue en el Jardín Inglés de Múnich. Ewald había propuesto un modelo resonador de cristales para su tesis, pero este modelo no podía validarse utilizando luz visible , ya que la longitud de onda era mucho mayor que el espaciamiento entre los resonadores. Von Laue se dio cuenta de que se necesitaba radiación electromagnética de una longitud de onda más corta, y sugirió que los rayos X podrían tener una longitud de onda comparable al espaciamiento en los cristales. Von Laue trabajó con dos técnicos, Walter Friedrich y su asistente Paul Knipping, para hacer brillar un haz de rayos X a través de un cristal de sulfato de cobre y registrar su patrón de difracción en una placa fotográfica . ^{[14] : 43} Después de ser revelada, la placa mostró anillos de puntos borrosos de forma aproximadamente elíptica. A pesar de la imagen cruda y poco clara, la imagen confirmó el concepto de difracción. Los resultados fueron presentados en la Academia Bávara de Ciencias y Humanidades en junio de 1912 con el título "Interferenz-Erscheinungen bei Röntgenstrahlen" (Fenómenos de interferencia en rayos X). ^{[15] [16]}

Después de ver los resultados iniciales, Laue estaba caminando hacia su casa y de repente concibió las leyes físicas que describen el efecto. ^{[14] : 44} Laue desarrolló una ley que conecta los ángulos de dispersión y el tamaño y la orientación de los espaciamientos de las celdas unitarias en el cristal, por la que recibió el Premio Nobel de Física en 1914. ^[17]

Después de la investigación pionera de Von Laue, el campo se desarrolló rápidamente, sobre todo por los físicos William Lawrence Bragg y su padre William Henry Bragg . En 1912-1913, el joven Bragg desarrolló la ley de Bragg , que conecta la dispersión con planos espaciados uniformemente dentro de un cristal. ^{[1] [18] [19] [20]} Los Bragg, padre e hijo, compartieron el Premio Nobel de Física de 1915 por su trabajo en cristalografía. Las primeras estructuras eran generalmente simples; a medida que los métodos computacionales y experimentales mejoraron en las décadas siguientes, se hizo posible deducir posiciones atómicas confiables para arreglos más complicados de átomos; consulte Cristalografía de rayos X para más detalles.

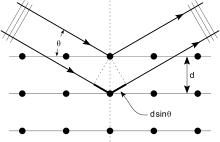
Los cristales son formaciones regulares de átomos y los rayos X son ondas electromagnéticas. Los átomos dispersan las ondas de rayos X, principalmente a través de los electrones de los átomos. Así como una ola del océano que choca contra un faro produce ondas circulares secundarias que emanan del faro, un rayo X que choca contra un electrón produce ondas esféricas secundarias que emanan del electrón. Este fenómeno se conoce como dispersión elástica y el electrón (o faro) se conoce como el dispersor . Una formación regular de dispersores produce una formación regular de ondas esféricas. Aunque estas ondas se cancelan entre sí en la mayoría de las direcciones a través de interferencias destructivas , se suman de manera constructiva en algunas direcciones específicas. ^{[21] [22] [23]}

Se puede obtener una comprensión intuitiva de la difracción de rayos X a partir del modelo de difracción de Bragg . En este modelo, una reflexión dada se asocia con un conjunto de láminas espaciadas uniformemente que recorren el cristal, generalmente pasando por los centros de los átomos de la red cristalina. La orientación de un conjunto particular de láminas se identifica por sus tres índices de Miller ( h , k , l ), ​​y su espaciamiento por d . William Lawrence Bragg propuso un modelo donde los rayos X entrantes se dispersan especularmente (como un espejo) desde cada plano; a partir de esa suposición, los rayos X dispersados ​​​​desde planos adyacentes se combinarán de manera constructiva ( interferencia constructiva ) cuando el ángulo θ entre el plano y el rayo X resulte en una diferencia de longitud de trayectoria que sea un múltiplo entero n de la longitud de onda de rayos X λ.

${\displaystyle 2d\sin\theta=n\lambda .}$

Se dice que una reflexión está indexada cuando sus índices de Miller (o, más correctamente, sus componentes recíprocos del vector reticular) se han identificado a partir de la longitud de onda conocida y el ángulo de dispersión 2θ. Dicha indexación proporciona los parámetros de la celda unitaria , las longitudes y los ángulos de la celda unitaria, así como su grupo espacial . ^[21]

Cada patrón de difracción de rayos X representa una porción esférica del espacio recíproco, como se puede ver en la construcción de la esfera de Ewald. Para un vector de onda incidente k ₀ dado , los únicos vectores de onda con la misma energía se encuentran en la superficie de una esfera. En el diagrama, el vector de onda k ₁ se encuentra en la esfera de Ewald y también está en un vector reticular recíproco g _1, por lo que satisface la ley de Bragg. En contraste, el vector de onda k ₂ difiere del punto reticular recíproco y g ₂ por el vector s , que se denomina error de excitación. Para los monocristales grandes utilizados principalmente en cristalografía, solo importa el caso de la ley de Bragg; para la difracción de electrones y algunos otros tipos de difracción de rayos X, también importan los valores distintos de cero del error de excitación. ^[23]

La dispersión de rayos X está determinada por la densidad de electrones dentro del cristal. Dado que la energía de un rayo X es mucho mayor que la de un electrón de valencia, la dispersión puede modelarse como dispersión de Thomson , la interacción elástica de un rayo electromagnético con una partícula cargada.

La intensidad de la dispersión de Thomson para una partícula con masa m y carga elemental q es: ^[22]

${\displaystyle I_{o}=I_{e}\left({\frac {q^{4}}{m^{2}c^{4}}}\right){\frac {1+\cos ^{2}2\theta }{2}}=I_{e}7,94\times 10^{-26}{\frac {1+\cos ^{2}2\theta }{2}}=I_{e}f}$

Por lo tanto, los núcleos atómicos, que son mucho más pesados ​​que un electrón, contribuyen de manera insignificante a los rayos X dispersados. En consecuencia, la dispersión coherente detectada de un átomo se puede aproximar con precisión analizando la dispersión colectiva de los electrones en el sistema. ^[21]

El haz de rayos X entrante tiene una polarización y debe representarse como una onda vectorial; sin embargo, para simplificar, se representará aquí como una onda escalar. Ignoraremos la dependencia temporal de la onda y nos concentraremos únicamente en la dependencia espacial de la onda. Las ondas planas se pueden representar mediante un vector de onda k _en , por lo que la onda entrante en el momento t  = 0 viene dada por

${\displaystyle A\mathrm {e} ^{2\pi \mathrm {i} \mathbf {k} _{\mathrm {in} }\cdot \mathbf {r} }.}$

En una posición r dentro de la muestra, considere una densidad de dispersores f ( r ); estos dispersores producen una onda esférica dispersa de amplitud proporcional a la amplitud local de la onda entrante multiplicada por el número de dispersores en un volumen pequeño dV alrededor de r

${\displaystyle {\text{amplitud de onda dispersada}}=A\mathrm {e} ^{2\pi \mathrm {i} \mathbf {k} \cdot \mathbf {r} }Sf(\mathbf {r} )\,\mathrm {d} V,}$

donde S es la constante de proporcionalidad.

Considere la fracción de ondas dispersas que salen con un vector de onda saliente de k _out y chocan contra una pantalla (detector) en r _screen . Como no se pierde energía (dispersión elástica, no inelástica), las longitudes de onda son las mismas que las magnitudes de los vectores de onda | k _in | = | k _out |. Desde el momento en que el fotón se dispersa en r hasta que se absorbe en r _screen , el fotón sufre un cambio de fase.

${\displaystyle e^{2\pi i\mathbf {k} _{\text{salida}}\cdot \left(\mathbf {r} _{\text{pantalla}}-\mathbf {r} \right)}.}$

La radiación neta que llega a _{la pantalla} r es la suma de todas las ondas dispersas a lo largo del cristal.

${\displaystyle AS\int \mathrm {d} \mathbf {r} \,f(\mathbf {r} )\mathrm {e} ^{2\pi \mathrm {i} \mathbf {k} _{\text {in}}\cdot \mathbf {r} }e^{2\pi i\mathbf {k} _{\text{out}}\cdot \left(\mathbf {r} _{\text{pantalla}} -\mathbf {r} \right)}=ASe^{2\pi i\mathbf {k} _{\text{out}}\cdot \mathbf {r} _{\text{pantalla}}}\int \ mathrm {d} \mathbf {r} \,f(\mathbf {r} )\mathrm {e} ^{2\pi \mathrm {i} \left(\mathbf {k} _{\text{en}}-\mathbf {k} _{\text{fuera}}\derecha)\cdot \mathbf {r} },}$

que puede escribirse como una transformada de Fourier

${\displaystyle AS\mathrm {e} ^{2\pi \mathrm {i} \mathbf {k} _{\text{salida}}\cdot \mathbf {r} _{\text{pantalla}}}\int d\mathbf {r} f(\mathbf {r} )\mathrm {e} ^{-2\pi \mathrm {i} \mathbf {g} \cdot \mathbf {r} }=AS\mathrm {e} ^{2\pi \mathrm {i} \mathbf {k} _{\text{salida}}\cdot \mathbf {r} _{\text{pantalla}}}F(\mathbf {g} ),}$

donde g = k _out  –  k _in es un vector reticular recíproco que satisface la ley de Bragg y la construcción de Ewald mencionadas anteriormente. La intensidad medida de la reflexión será el cuadrado de esta amplitud ^{[21] [22]}

${\displaystyle A^{2}S^{2}\izquierda|F(\mathbf {g} )\derecha|^{2}.}$

Lo anterior supone que las regiones cristalinas son algo grandes, por ejemplo de micrones de diámetro, pero tampoco tan grandes como para que los rayos X se dispersen más de una vez. Si no es así, las intensidades difractadas serán aún más complicadas. ^{[23] [24]}

Los experimentos de difracción a pequeña escala se pueden realizar con una fuente de tubo de rayos X local , normalmente acoplada a un detector de placa de imagen . Estos tienen la ventaja de ser relativamente económicos y fáciles de mantener, y permiten una rápida selección y recolección de muestras. Sin embargo, la longitud de onda de los rayos X producidos está limitada por la disponibilidad de diferentes materiales de ánodo . Además, la intensidad está limitada por la potencia aplicada y la capacidad de enfriamiento disponible para evitar la fusión del ánodo. En tales sistemas, los electrones se desprenden de un cátodo y se aceleran a través de un fuerte potencial eléctrico de ~50  kV ; habiendo alcanzado una alta velocidad, los electrones chocan con una placa de metal, emitiendo bremsstrahlung y algunas líneas espectrales fuertes correspondientes a la excitación de los electrones de la capa interna del metal. El metal más común utilizado es el cobre, que se puede mantener frío fácilmente debido a su alta conductividad térmica , y que produce fuertes líneas K _α y K _β . La línea K _β a veces se suprime con una fina lámina de níquel (~10 μm). La variedad más simple y económica de tubo de rayos X sellado tiene un ánodo estacionario (el tubo de Crookes ) y funciona con una potencia de haz de electrones de ~2 kW. La variedad más cara tiene una fuente de tipo ánodo rotatorio que funciona con una potencia de haz de electrones de ~14 kW.

Los rayos X generalmente se filtran (mediante el uso de filtros de rayos X ) a una única longitud de onda (se vuelven monocromáticos) y se coliman en una única dirección antes de permitir que lleguen al cristal. El filtrado no solo simplifica el análisis de datos, sino que también elimina la radiación que degrada el cristal sin aportar información útil. La colimación se realiza con un colimador (básicamente, un tubo largo) o con una disposición de espejos suavemente curvados. Los sistemas de espejos son los preferidos para cristales pequeños (menos de 0,3 mm) o con celdas unitarias grandes (más de 150 Å).

Un desarrollo más reciente es el tubo de microfoco , que puede proporcionar un flujo de haz al menos tan alto (después de la colimación) como las fuentes de ánodo giratorio, pero solo requiere una potencia de haz de unas pocas decenas o cientos de vatios en lugar de requerir varios kilovatios.

Las fuentes de radiación de sincrotrón son algunas de las fuentes de luz más brillantes de la Tierra y constituyen unas de las herramientas más potentes disponibles para la difracción de rayos X y la cristalografía. Los rayos X se generan en sincrotrones que aceleran partículas cargadas eléctricamente, a menudo electrones, a casi la velocidad de la luz y las confinan en un bucle (aproximadamente) circular utilizando campos magnéticos.

Los sincrotrones son instalaciones nacionales, cada una de ellas con varias líneas de luz dedicadas a recoger datos sin interrupción. Los sincrotrones fueron diseñados originalmente para que los utilizaran los físicos de alta energía que estudiaban partículas subatómicas y fenómenos cósmicos . El componente más grande de cada sincrotrón es su anillo de almacenamiento de electrones. Este anillo no es un círculo perfecto, sino un polígono de múltiples lados. En cada esquina del polígono, o sector, unos imanes alineados con precisión curvan el flujo de electrones. A medida que se curva la trayectoria de los electrones, estos emiten ráfagas de energía en forma de rayos X.

La intensa radiación ionizante puede causar daños por radiación a las muestras, particularmente a los cristales macromoleculares. La criocristalografía puede proteger la muestra del daño por radiación, congelando el cristal a temperaturas de nitrógeno líquido (~100 K ). ^[25] Los métodos de criocristalografía también se aplican a fuentes de ánodo rotatorio de fuente casera. ^[26] Sin embargo, la radiación de sincrotrón con frecuencia tiene la ventaja de longitudes de onda seleccionables por el usuario, lo que permite experimentos de dispersión anómala que maximizan la señal anómala. Esto es fundamental en experimentos como la dispersión anómala de longitud de onda única (SAD) y la dispersión anómala de longitud de onda múltiple (MAD).

Los láseres de electrones libres se han desarrollado para su uso en difracción de rayos X y cristalografía. ^[27] Estas son las fuentes de rayos X más brillantes disponibles actualmente; los rayos X llegan en ráfagas de femtosegundos . La intensidad de la fuente es tal que los patrones de difracción de resolución atómica se pueden resolver para cristales que de otro modo serían demasiado pequeños para su recolección. Sin embargo, la fuente de luz intensa también destruye la muestra, ^[28] lo que requiere que se disparen múltiples cristales. Como cada cristal está orientado aleatoriamente en el haz, se deben recolectar cientos de miles de imágenes de difracción individuales para obtener un conjunto de datos completo. Este método, la cristalografía de femtosegundos en serie , se ha utilizado para resolver la estructura de varias estructuras cristalinas de proteínas, notando a veces diferencias con estructuras equivalentes recolectadas de fuentes de sincrotrón. ^[29]

Otras formas de dispersión elástica de rayos X además de la difracción de monocristal incluyen la difracción de polvo , la dispersión de rayos X de ángulo pequeño ( SAXS ) y varios tipos de difracción de rayos X por fibra , que fue utilizada por Rosalind Franklin para determinar la estructura de doble hélice del ADN . En general, la difracción de rayos X de monocristal ofrece más información estructural que estas otras técnicas; sin embargo, requiere un cristal suficientemente grande y regular, que no siempre está disponible.

Estos métodos de dispersión generalmente utilizan rayos X monocromáticos , que están restringidos a una única longitud de onda con desviaciones menores. También se puede utilizar un amplio espectro de rayos X (es decir, una mezcla de rayos X con diferentes longitudes de onda) para llevar a cabo la difracción de rayos X, una técnica conocida como el método de Laue. Este es el método utilizado en el descubrimiento original de la difracción de rayos X. La dispersión de Laue proporciona mucha información estructural con solo una corta exposición al haz de rayos X y, por lo tanto, se utiliza en estudios estructurales de eventos muy rápidos ( cristalografía resuelta en el tiempo ). Sin embargo, no es tan adecuada como la dispersión monocromática para determinar la estructura atómica completa de un cristal y, por lo tanto, funciona mejor con cristales con disposiciones atómicas relativamente simples.

El modo de reflexión posterior de Laue registra los rayos X dispersados ​​hacia atrás desde una fuente de amplio espectro. Esto resulta útil si la muestra es demasiado gruesa para que los rayos X se transmitan a través de ella. Los planos de difracción en el cristal se determinan sabiendo que la normal al plano de difracción biseca el ángulo entre el haz incidente y el haz difractado. Se puede utilizar un diagrama de Greninger ^[30] para interpretar la fotografía de Laue de reflexión posterior.

Debido a que interactúan a través de las fuerzas de Coulomb, la dispersión de electrones por la materia es 1000 o más veces más fuerte que la de los rayos X. Por lo tanto, los haces de electrones producen una fuerte dispersión múltiple o dinámica incluso para cristales relativamente delgados (>10 nm). Si bien existen similitudes entre la difracción de rayos X y electrones, como se puede encontrar en el libro de John M. Cowley , ^[23] el enfoque es diferente ya que se basa en el enfoque original de Hans Bethe ^[31] y en la resolución de la ecuación de Schrödinger para electrones relativistas , en lugar de un enfoque cinemático o de la ley de Bragg . Es posible obtener información sobre regiones muy pequeñas, hasta átomos individuales. La gama de aplicaciones de la difracción de electrones , la microscopía electrónica de transmisión y la cristalografía electrónica de transmisión con electrones de alta energía es amplia; consulte los enlaces relevantes para obtener más información y citas. Además de los métodos de transmisión, la difracción de electrones de baja energía ^[32] es una técnica en la que los electrones se retrodispersan desde las superficies y se ha utilizado ampliamente para determinar las estructuras de la superficie a escala atómica, y la difracción de electrones de alta energía por reflexión es otra que se utiliza ampliamente para monitorear el crecimiento de películas delgadas. ^[33]

La difracción de neutrones se utiliza para la determinación de la estructura, aunque ha sido difícil obtener haces intensos y monocromáticos de neutrones en cantidades suficientes. Tradicionalmente, se han utilizado reactores nucleares , aunque cada vez hay más fuentes que producen neutrones por espalación . Al no tener carga, los neutrones se dispersan más desde los núcleos atómicos que desde los electrones. Por lo tanto, la dispersión de neutrones es útil para observar las posiciones de átomos ligeros con pocos electrones, especialmente hidrógeno , que es esencialmente invisible en la difracción de rayos X. La dispersión de neutrones también tiene la propiedad de que el disolvente puede hacerse invisible ajustando la proporción de agua normal, H ₂ O, y agua pesada , D ₂ O.