Efecto fotoeléctrico
Emisión de electrones cuando la radiación electromagnética incide sobre un material.
Fotoemisión de electrones desde una placa metálica acompañada de la absorción de cuantos de luz: fotones.

El efecto fotoeléctrico es la emisión de electrones de un material causada por la radiación electromagnética , como la luz ultravioleta . Los electrones emitidos de esta manera se denominan fotoelectrones. El fenómeno se estudia en física de la materia condensada , estado sólido y química cuántica para extraer conclusiones sobre las propiedades de los átomos, las moléculas y los sólidos. El efecto se ha utilizado en dispositivos electrónicos especializados en la detección de luz y la emisión de electrones en un tiempo preciso.

Los resultados experimentales no concuerdan con el electromagnetismo clásico , que predice que las ondas de luz continuas transfieren energía a los electrones, que luego se emitirían cuando acumularan suficiente energía. Una alteración en la intensidad de la luz cambiaría teóricamente la energía cinética de los electrones emitidos, y una luz suficientemente tenue daría como resultado una emisión retardada. Los resultados experimentales, en cambio, muestran que los electrones se desprenden solo cuando la luz excede una cierta frecuencia , independientemente de la intensidad de la luz o la duración de la exposición. Debido a que un haz de baja frecuencia a una alta intensidad no acumula la energía necesaria para producir fotoelectrones, como sería el caso si la energía de la luz se acumulara con el tiempo a partir de una onda continua, Albert Einstein propuso que un haz de luz no es una onda que se propaga a través del espacio, sino un enjambre de paquetes de energía discretos, conocidos como fotones , término acuñado por Gilbert N. Lewis en 1926. [1]

La emisión de electrones de conducción de metales típicos requiere unos cuantos cuantos de luz de electrón-voltio (eV), correspondientes a la luz visible o ultravioleta de longitud de onda corta. En casos extremos, las emisiones se inducen con fotones que se acercan a la energía cero, como en sistemas con afinidad electrónica negativa y la emisión de estados excitados, o unos pocos cientos de fotones de keV para electrones centrales en elementos con un alto número atómico . [2] El estudio del efecto fotoeléctrico condujo a pasos importantes en la comprensión de la naturaleza cuántica de la luz y los electrones e influyó en la formación del concepto de dualidad onda-partícula . [3] Otros fenómenos en los que la luz afecta el movimiento de cargas eléctricas incluyen el efecto fotoconductor , el efecto fotovoltaico y el efecto fotoelectroquímico .

Mecanismo de emisión

Los fotones de un haz de luz tienen una energía característica, llamada energía fotónica , que es proporcional a la frecuencia de la luz. En el proceso de fotoemisión, cuando un electrón dentro de algún material absorbe la energía de un fotón y adquiere más energía que su energía de enlace , es probable que sea expulsado. Si la energía del fotón es demasiado baja, el electrón no puede escapar del material. Dado que un aumento en la intensidad de la luz de baja frecuencia solo aumentará el número de fotones de baja energía, este cambio en la intensidad no creará ningún fotón individual con suficiente energía para desalojar a un electrón. Además, la energía de los electrones emitidos no dependerá de la intensidad de la luz entrante de una frecuencia dada, sino solo de la energía de los fotones individuales. [4]

Mientras que los electrones libres pueden absorber cualquier energía cuando son irradiados siempre que esto sea seguido por una reemisión inmediata, como en el efecto Compton , en los sistemas cuánticos toda la energía de un fotón es absorbida (si la mecánica cuántica permite el proceso ) o ninguna en absoluto. Parte de la energía adquirida se utiliza para liberar al electrón de su enlace atómico, y el resto contribuye a la energía cinética del electrón como partícula libre. [5] [6] [7] Debido a que los electrones en un material ocupan muchos estados cuánticos diferentes con diferentes energías de enlace, y debido a que pueden sufrir pérdidas de energía en su camino fuera del material, los electrones emitidos tendrán un rango de energías cinéticas. Los electrones de los estados más ocupados tendrán la energía cinética más alta. En los metales, esos electrones serán emitidos desde el nivel de Fermi .

Cuando el fotoelectrón se emite en un sólido en lugar de en el vacío, a menudo se utiliza el término fotoemisión interna y la emisión en el vacío se distingue como fotoemisión externa .

Observación experimental de la emisión fotoeléctrica.

Aunque la fotoemisión puede producirse a partir de cualquier material, se observa con mayor facilidad en metales y otros conductores. Esto se debe a que el proceso produce un desequilibrio de carga que, si no se neutraliza mediante el flujo de corriente, da lugar a una barrera de potencial cada vez mayor hasta que la emisión cesa por completo. La barrera de energía para la fotoemisión suele aumentar con capas de óxido no conductor sobre superficies metálicas, por lo que la mayoría de los experimentos y dispositivos prácticos basados ​​en el efecto fotoeléctrico utilizan superficies metálicas limpias en tubos de vacío. El vacío también ayuda a observar los electrones, ya que evita que los gases impidan su flujo entre los electrodos. [ cita requerida ]

Como la luz solar, debido a la absorción de la atmósfera, no proporciona mucha luz ultravioleta, la luz rica en rayos ultravioleta solía obtenerse quemando magnesio o con una lámpara de arco . En la actualidad, prevalecen las lámparas de vapor de mercurio , las lámparas UV de descarga de gas noble y las fuentes de plasma de radiofrecuencia , [8] [9] [10] los láseres ultravioleta [ 11] y los dispositivos de inserción de sincrotrón [12] .

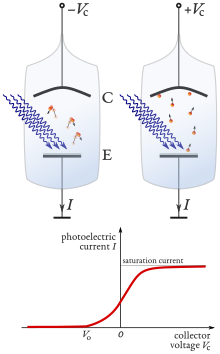
Esquema del experimento para demostrar el efecto fotoeléctrico. La luz monocromática filtrada de una determinada longitud de onda incide en el electrodo emisor (E) dentro de un tubo de vacío. El electrodo colector (C) está polarizado a un voltaje V C que puede ajustarse para atraer los electrones emitidos, cuando es positivo, o para evitar que alguno de ellos llegue al colector, cuando es negativo.

La configuración clásica para observar el efecto fotoeléctrico incluye una fuente de luz, un conjunto de filtros para monocromatizar la luz, un tubo de vacío transparente a la luz ultravioleta, un electrodo emisor (E) expuesto a la luz y un colector (C) cuyo voltaje V C puede controlarse externamente. [ cita requerida ]

Se utiliza un voltaje externo positivo para dirigir los electrones fotoemitidos hacia el colector. Si la frecuencia y la intensidad de la radiación incidente son fijas, la corriente fotoeléctrica I aumenta con un aumento en el voltaje positivo, a medida que se dirigen más y más electrones hacia el electrodo. Cuando no se pueden recolectar fotoelectrones adicionales, la corriente fotoeléctrica alcanza un valor de saturación. Esta corriente solo puede aumentar con el aumento de la intensidad de la luz. [ cita requerida ]

Un voltaje negativo creciente impide que todos los electrones, excepto los de mayor energía, lleguen al colector. Cuando no se observa corriente a través del tubo, el voltaje negativo ha alcanzado el valor que es lo suficientemente alto como para frenar y detener los fotoelectrones más energéticos de energía cinética K max . Este valor del voltaje retardador se llama potencial de detención o potencial de corte V o . [13] Dado que el trabajo realizado por el potencial retardador para detener el electrón de carga e es eV o , debe cumplirse lo siguiente eV o  =  K max .

La curva corriente-voltaje es sigmoidea, pero su forma exacta depende de la geometría experimental y de las propiedades del material del electrodo.

Para una superficie metálica dada, existe una cierta frecuencia mínima de radiación incidente por debajo de la cual no se emiten fotoelectrones. Esta frecuencia se llama frecuencia umbral . Al aumentar la frecuencia del haz incidente, aumenta la energía cinética máxima de los fotoelectrones emitidos, y el voltaje de frenado debe aumentar. El número de electrones emitidos también puede cambiar porque la probabilidad de que cada fotón resulte en un electrón emitido es una función de la energía del fotón [ cita requerida ] .

Un aumento en la intensidad de la misma luz monocromática (siempre que la intensidad no sea demasiado alta [14] ), que es proporcional al número de fotones que inciden en la superficie en un tiempo dado, aumenta la velocidad a la que se expulsan los electrones (la corriente fotoeléctrica I) , pero la energía cinética de los fotoelectrones y el voltaje de frenado permanecen iguales. Para un metal y una frecuencia de radiación incidente determinados, la velocidad a la que se expulsan los fotoelectrones es directamente proporcional a la intensidad de la luz incidente.

El desfase temporal entre la incidencia de la radiación y la emisión de un fotoelectrón es muy pequeño, menos de 10 −9 segundos. La distribución angular de los fotoelectrones depende en gran medida de la polarización (la dirección del campo eléctrico) de la luz incidente, así como de las propiedades cuánticas del material emisor, como las simetrías orbitales atómicas y moleculares y la estructura de bandas electrónicas de los sólidos cristalinos. En materiales sin orden macroscópico, la distribución de electrones tiende a alcanzar su punto máximo en la dirección de polarización de la luz polarizada linealmente. [15] La técnica experimental que puede medir estas distribuciones para inferir las propiedades del material es la espectroscopia de fotoemisión con resolución angular .

Explicación teórica

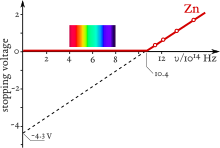
Diagrama de la energía cinética máxima en función de la frecuencia de la luz sobre el zinc.

En 1905, Einstein propuso una teoría del efecto fotoeléctrico utilizando un concepto según el cual la luz consiste en pequeños paquetes de energía conocidos como fotones o cuantos de luz. Cada paquete lleva energía que es proporcional a la frecuencia de la onda electromagnética correspondiente. La constante de proporcionalidad se conoce como la constante de Planck . En el rango de energías cinéticas de los electrones que se eliminan de sus enlaces atómicos variables por la absorción de un fotón de energía , la energía cinética más alta es Aquí, es la energía mínima requerida para eliminar un electrón de la superficie del material. Se llama función de trabajo de la superficie y a veces se denota o . [16] Si la función de trabajo se escribe como la fórmula para la energía cinética máxima de los electrones expulsados ​​se convierte en yo a {\estilo de visualización h\nu} a {\estilo de visualización \nu} yo {\estilo de visualización h} yo a {\estilo de visualización h\nu} K máximo {\displaystyle K_{\max}} K máximo = yo a − Yo . {\displaystyle K_{\max }=h\,\nu -W.} Yo {\estilo de visualización W} Φ {\estilo de visualización \Phi} φ {\estilo de visualización \varphi} Yo = yo a o , {\displaystyle W=h\,\nu _ {o},} K máximo = yo ( a − a o ) . {\displaystyle K_{\max }=h\left(\nu -\nu _ {o}\right).}

La energía cinética es positiva y es necesaria para que se produzca el efecto fotoeléctrico. [17] La ​​frecuencia es la frecuencia umbral para el material dado. Por encima de esa frecuencia, la energía cinética máxima de los fotoelectrones, así como el voltaje de frenado en el experimento, aumentan linealmente con la frecuencia y no dependen del número de fotones ni de la intensidad de la luz monocromática incidente. La fórmula de Einstein, por sencilla que fuera, explicaba toda la fenomenología del efecto fotoeléctrico y tuvo consecuencias de gran alcance en el desarrollo de la mecánica cuántica . a > a o {\displaystyle \nu >\nu _{o}} a o {\displaystyle \nu_{o}} V o = yo mi ( a − a o ) {\textstyle V_{o}={\frac {h}{e}}\left(\nu -\nu _ {o}\right)}

Fotoemisión de átomos, moléculas y sólidos.

Los electrones que se encuentran ligados en átomos, moléculas y sólidos ocupan estados distintos con energías de enlace bien definidas . Cuando los cuantos de luz entregan más que esta cantidad de energía a un electrón individual, el electrón puede ser emitido al espacio libre con un exceso de energía (cinética) que es mayor que la energía de enlace del electrón. La distribución de energías cinéticas refleja, por lo tanto, la distribución de las energías de enlace de los electrones en el sistema atómico, molecular o cristalino: un electrón emitido desde el estado con energía de enlace se encuentra con energía cinética . Esta distribución es una de las principales características del sistema cuántico y puede usarse para estudios posteriores en química cuántica y física cuántica. [ cita requerida ] yo a {\estilo de visualización h\nu} mi B Estilo de visualización E_{B} mi a = yo a − mi B {\displaystyle E_{k}=h\nu -E_{B}}

Modelos de fotoemisión de sólidos

Las propiedades electrónicas de los sólidos cristalinos ordenados están determinadas por la distribución de los estados electrónicos con respecto a la energía y el momento (la estructura de bandas electrónicas del sólido). Los modelos teóricos de fotoemisión de sólidos muestran que esta distribución se conserva, en su mayor parte, en el efecto fotoeléctrico. El modelo fenomenológico de tres pasos [18] para la excitación ultravioleta y de rayos X suaves descompone el efecto en estos pasos: [19] [20] [21]

  1. Efecto fotoeléctrico interno en la masa del material que es una transición óptica directa entre un estado electrónico ocupado y uno desocupado. Este efecto está sujeto a reglas de selección mecánico-cuánticas para transiciones dipolares. El hueco que queda detrás del electrón puede dar lugar a una emisión secundaria de electrones, o el llamado efecto Auger , que puede ser visible incluso cuando el fotoelectrón primario no abandona el material. En los sólidos moleculares, los fonones se excitan en este paso y pueden ser visibles como líneas satélite en la energía final del electrón.
  2. Propagación de electrones a la superficie, en la que algunos electrones pueden estar dispersos debido a interacciones con otros constituyentes del sólido. Los electrones que se originan en las capas más profundas del sólido tienen muchas más probabilidades de sufrir colisiones y emerger con energía y momento alterados. Su trayectoria libre media es una curva universal que depende de la energía del electrón.
  3. Los electrones escapan a través de la barrera superficial hacia estados similares a los de los electrones libres en el vacío. En este paso, el electrón pierde energía en la cantidad de la función de trabajo de la superficie y sufre la pérdida de momento en la dirección perpendicular a la superficie. Debido a que la energía de enlace de los electrones en los sólidos se expresa convenientemente con respecto al estado ocupado más alto en la energía de Fermi y la diferencia con la energía del espacio libre (vacío) es la función de trabajo de la superficie, la energía cinética de los electrones emitidos desde los sólidos generalmente se escribe como . mi F Estilo de visualización E_ {F}} mi a = yo a − Yo − mi B {\displaystyle E_{k}=h\nu -W-E_{B}}

Existen casos en los que el modelo de tres pasos no logra explicar las peculiaridades de las distribuciones de intensidad de los fotoelectrones. El modelo de un solo paso, más elaborado [22], trata el efecto como un proceso coherente de fotoexcitación hacia el estado final de un cristal finito para el cual la función de onda es similar a la de los electrones libres fuera del cristal, pero tiene una envoltura en descomposición en su interior. [21]

Historia

Siglo XIX

En 1839, Alexandre Edmond Becquerel descubrió el efecto fotovoltaico relacionado mientras estudiaba el efecto de la luz en las células electrolíticas . [23] Aunque no es equivalente al efecto fotoeléctrico, su trabajo sobre energía fotovoltaica fue fundamental para demostrar una fuerte relación entre la luz y las propiedades electrónicas de los materiales. En 1873, Willoughby Smith descubrió la fotoconductividad en el selenio mientras probaba el metal por sus propiedades de alta resistencia en conjunto con su trabajo sobre cables telegráficos submarinos. [24]

Johann Elster (1854-1920) y Hans Geitel (1855-1923), estudiantes en Heidelberg , investigaron los efectos producidos por la luz en cuerpos electrificados y desarrollaron las primeras células fotoeléctricas prácticas que podían usarse para medir la intensidad de la luz. [25] [26] : 458  Ordenaron los metales con respecto a su poder de descarga de electricidad negativa: rubidio , potasio , aleación de potasio y sodio, sodio , litio , magnesio , talio y zinc ; para el cobre , platino , plomo , hierro , cadmio , carbono y mercurio, los efectos con la luz ordinaria eran demasiado pequeños para ser medibles. El orden de los metales para este efecto fue el mismo que en la serie de Volta para la electricidad de contacto, siendo los metales más electropositivos los que dieron el mayor efecto fotoeléctrico.

Electroscopio de hoja de oro que demuestra el efecto fotoeléctrico. Cuando el disco del electroscopio se carga negativamente con un exceso de electrones, las hojas de oro se repelen entre sí. Si se proyecta una luz de alta energía (como la ultravioleta) sobre el disco, se emiten electrones por el efecto fotoeléctrico y cesa la repulsión de las hojas. Pero si la luz utilizada no tiene suficiente energía para estimular la emisión de electrones, las hojas permanecen separadas independientemente de la duración.

En 1887, Heinrich Hertz observó el efecto fotoeléctrico [27] e informó sobre la producción y recepción [28] de ondas electromagnéticas. [29] El receptor de su aparato consistía en una bobina con un espacio de chispa , donde se vería una chispa al detectar ondas electromagnéticas. Colocó el aparato en una caja oscura para ver mejor la chispa. Sin embargo, notó que la longitud máxima de la chispa se reducía dentro de la caja. Un panel de vidrio colocado entre la fuente de ondas electromagnéticas y el receptor absorbía la radiación ultravioleta que ayudaba a los electrones a saltar a través del espacio. Cuando se retiraba, la longitud de la chispa aumentaba. No observó ninguna disminución en la longitud de la chispa cuando reemplazó el vidrio con cuarzo, ya que el cuarzo no absorbe la radiación UV. [ cita requerida ]

Los descubrimientos de Hertz dieron lugar a una serie de investigaciones por parte de Wilhelm Hallwachs , [30] [31] Hoor, [32] Augusto Righi [33] y Aleksander Stoletov [34] [35] sobre el efecto de la luz, y especialmente de la luz ultravioleta, sobre los cuerpos cargados. Hallwachs conectó una placa de zinc a un electroscopio . Dejó que la luz ultravioleta cayera sobre una placa de zinc recién limpiada y observó que la placa de zinc se descargaba si inicialmente estaba cargada negativamente, se cargaba positivamente si inicialmente estaba descargada y se cargaba más positivamente si inicialmente estaba cargada positivamente. A partir de estas observaciones, concluyó que la placa de zinc emitía algunas partículas cargadas negativamente cuando se exponía a la luz ultravioleta.

En lo que respecta al efecto Hertz , los investigadores demostraron desde el principio la complejidad del fenómeno de la fatiga fotoeléctrica, es decir, la disminución progresiva del efecto que se observa en superficies metálicas frescas. Según Hallwachs, el ozono desempeñaba un papel importante en el fenómeno [36] y la emisión se veía influida por la oxidación, la humedad y el grado de pulido de la superficie. En aquel momento no estaba claro si la fatiga no existía en el vacío. [ cita requerida ]

En el período de 1888 a 1891, Aleksandr Stoletov realizó un análisis detallado del fotoefecto, cuyos resultados se publicaron en seis publicaciones. [35] Stoletov inventó una nueva configuración experimental que era más adecuada para un análisis cuantitativo del fotoefecto. Descubrió una proporcionalidad directa entre la intensidad de la luz y la corriente fotoeléctrica inducida (la primera ley del fotoefecto o ley de Stoletov ). Midió la dependencia de la intensidad de la corriente fotoeléctrica con la presión del gas, donde encontró la existencia de una presión de gas óptima correspondiente a una fotocorriente máxima ; esta propiedad se utilizó para la creación de células solares . [ cita requerida ]

Además de los metales, muchas otras sustancias descargan electricidad negativa bajo la acción de la luz ultravioleta. GC Schmidt [37] y O. Knoblauch [38] elaboraron una lista de estas sustancias.

En 1897, J. J. Thomson investigó la luz ultravioleta en los tubos de Crookes . [39] Thomson dedujo que las partículas expulsadas, a las que llamó corpúsculos, eran de la misma naturaleza que los rayos catódicos . Estas partículas más tarde se conocerían como electrones. Thomson encerró una placa de metal (un cátodo) en un tubo de vacío y la expuso a radiación de alta frecuencia. [40] Se pensaba que los campos electromagnéticos oscilantes causaban que el campo de los átomos resonara y, después de alcanzar una cierta amplitud, causaban que se emitieran corpúsculos subatómicos y que se detectara corriente. La cantidad de esta corriente variaba con la intensidad y el color de la radiación. Una mayor intensidad o frecuencia de radiación produciría más corriente. [ cita requerida ]

Durante los años 1886-1902, Wilhelm Hallwachs y Philipp Lenard investigaron en detalle el fenómeno de la emisión fotoeléctrica. Lenard observó que una corriente fluye a través de un tubo de vidrio al vacío que encierra dos electrodos cuando la radiación ultravioleta incide sobre uno de ellos. Tan pronto como la radiación ultravioleta se detiene, la corriente también se detiene. Esto inició el concepto de emisión fotoeléctrica. El descubrimiento de la ionización de los gases por la luz ultravioleta fue realizado por Philipp Lenard en 1900. Como el efecto se producía a lo largo de varios centímetros de aire y producía un mayor número de iones positivos que negativos, era natural interpretar el fenómeno, como lo hizo JJ Thomson, como un efecto de Hertz sobre las partículas presentes en el gas. [29]

Siglo XX

En 1902, Lenard observó que la energía de los electrones individuales emitidos era independiente de la intensidad de la luz aplicada. [5] [41] Esto parecía estar en desacuerdo con la teoría ondulatoria de la luz de Maxwell , que predijo que la energía del electrón sería proporcional a la intensidad de la radiación.

Lenard observó la variación de la energía de los electrones con la frecuencia de la luz utilizando una potente lámpara de arco eléctrico que le permitió investigar grandes cambios en la intensidad. Sin embargo, los resultados de Lenard fueron cualitativos en lugar de cuantitativos debido a la dificultad de realizar los experimentos: los experimentos debían realizarse en metal recién cortado para poder observar el metal puro, pero se oxidaba en cuestión de minutos incluso en los vacíos parciales que utilizó. La corriente emitida por la superficie estaba determinada por la intensidad de la luz, o brillo: al duplicar la intensidad de la luz, se duplicaba el número de electrones emitidos desde la superficie. [ cita requerida ]

Las investigaciones iniciales del efecto fotoeléctrico en gases por Lenard [42] fueron continuadas por JJ Thomson [43] y luego de manera más decisiva por Frederic Palmer Jr. [44] [45] La fotoemisión de gases fue estudiada y mostró características muy diferentes a las que inicialmente le atribuyó Lenard. [29]

En 1900, mientras estudiaba la radiación del cuerpo negro , el físico alemán Max Planck sugirió en su artículo "Sobre la ley de distribución de la energía en el espectro normal" [46] que la energía transportada por las ondas electromagnéticas solo podía liberarse en paquetes de energía. En 1905, Albert Einstein publicó un artículo en el que planteaba la hipótesis de que la energía de la luz se transporta en paquetes cuantizados discretos para explicar los datos experimentales del efecto fotoeléctrico. Einstein teorizó que la energía en cada cuanto de luz era igual a la frecuencia de la luz multiplicada por una constante, más tarde llamada constante de Planck . Un fotón por encima de una frecuencia umbral tiene la energía necesaria para expulsar un solo electrón, creando el efecto observado. Este fue un paso en el desarrollo de la mecánica cuántica . En 1914, las mediciones altamente precisas de Robert A. Millikan de la constante de Planck a partir del efecto fotoeléctrico respaldaron el modelo de Einstein, aunque una teoría corpuscular de la luz era para Millikan, en ese momento, "bastante impensable". [47] Einstein recibió el Premio Nobel de Física en 1921 por "su descubrimiento de la ley del efecto fotoeléctrico", [48] y Millikan recibió el Premio Nobel en 1923 por "su trabajo sobre la carga elemental de la electricidad y sobre el efecto fotoeléctrico". [49] En la teoría de perturbación cuántica de átomos y sólidos sobre los que actúa la radiación electromagnética, el efecto fotoeléctrico todavía se analiza comúnmente en términos de ondas; los dos enfoques son equivalentes porque la absorción de fotones u ondas solo puede ocurrir entre niveles de energía cuantizados cuya diferencia de energía es la de la energía del fotón. [50] [19]

La descripción matemática de Albert Einstein de cómo el efecto fotoeléctrico era causado por la absorción de cuantos de luz se encontraba en uno de sus artículos Annus Mirabilis , llamado "Sobre un punto de vista heurístico concerniente a la producción y transformación de la luz". [51] El artículo proponía una descripción simple de los cuantos de energía y mostraba cómo explicaban el espectro de radiación del cuerpo negro. Su explicación en términos de absorción de cuantos discretos de luz concordaba con los resultados experimentales. Explicaba por qué la energía de los fotoelectrones no dependía de la intensidad de la luz incidente . Este fue un salto teórico, pero el concepto fue fuertemente resistido al principio porque contradecía la teoría ondulatoria de la luz que se desprendía naturalmente de las ecuaciones de electromagnetismo de James Clerk Maxwell y, más generalmente, la suposición de divisibilidad infinita de la energía en los sistemas físicos.

El trabajo de Einstein predijo que la energía de los electrones individuales expulsados ​​aumenta linealmente con la frecuencia de la luz. La relación precisa no había sido probada en ese momento. En 1905 se sabía que la energía de los fotoelectrones aumenta con el aumento de la frecuencia de la luz incidente y es independiente de la intensidad de la luz. Sin embargo, la forma del aumento no se determinó experimentalmente hasta 1914, cuando Millikan demostró que la predicción de Einstein era correcta. [6]

El efecto fotoeléctrico ayudó a impulsar el concepto entonces emergente de dualidad onda-partícula en la naturaleza de la luz. La luz posee simultáneamente las características tanto de las ondas como de las partículas, cada una de las cuales se manifiesta de acuerdo con las circunstancias. El efecto era imposible de entender en términos de la descripción clásica de la luz como onda, [52] [53] [54] ya que la energía de los electrones emitidos no dependía de la intensidad de la radiación incidente. La teoría clásica predecía que los electrones "acumularían" energía durante un período de tiempo y luego serían emitidos. [53] [55]

Usos y efectos

Fotomultiplicadores

Fotomultiplicador

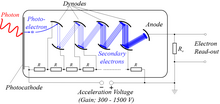
Se trata de tubos de vacío extremadamente sensibles a la luz con un fotocátodo recubierto en el interior de la envoltura. El fotocátodo contiene combinaciones de materiales como cesio, rubidio y antimonio especialmente seleccionados para proporcionar una función de trabajo baja, de modo que cuando se ilumina incluso con niveles muy bajos de luz, el fotocátodo libera fácilmente electrones. Por medio de una serie de electrodos (dínodos) a potenciales cada vez más altos, estos electrones se aceleran y aumentan sustancialmente en número a través de la emisión secundaria para proporcionar una corriente de salida fácilmente detectable. Los fotomultiplicadores todavía se utilizan comúnmente donde sea necesario detectar niveles bajos de luz. [56]

Sensores de imagen

Los tubos de las cámaras de vídeo de los primeros tiempos de la televisión utilizaban el efecto fotoeléctrico. Por ejemplo, el « Disector de imágenes » de Philo Farnsworth utilizaba una pantalla cargada por el efecto fotoeléctrico para transformar una imagen óptica en una señal electrónica escaneada. [57]

Espectroscopia fotoelectrónica

Experimento de espectroscopia de fotoemisión con resolución angular ( ARPES ). La lámpara de descarga de helio proyecta luz ultravioleta sobre la muestra en un vacío ultraalto. El analizador de electrones hemisférico mide la distribución de los electrones expulsados ​​con respecto a la energía y el momento.

Como la energía cinética de los electrones emitidos es exactamente la energía del fotón incidente menos la energía de la unión del electrón dentro de un átomo, molécula o sólido, la energía de unión se puede determinar haciendo brillar una luz UV o de rayos X monocromáticos de una energía conocida y midiendo las energías cinéticas de los fotoelectrones. [19] La distribución de las energías de los electrones es valiosa para estudiar las propiedades cuánticas de estos sistemas. También se puede utilizar para determinar la composición elemental de las muestras. Para los sólidos, se mide la energía cinética y la distribución del ángulo de emisión de los fotoelectrones para la determinación completa de la estructura de la banda electrónica en términos de las energías de unión permitidas y los momentos de los electrones. Los instrumentos modernos para la espectroscopia de fotoemisión con resolución angular son capaces de medir estas cantidades con una precisión mejor que 1 meV y 0,1°. [ cita requerida ]

Las mediciones de espectroscopia fotoelectrónica se realizan generalmente en un entorno de alto vacío, porque los electrones se dispersarían por las moléculas de gas si estuvieran presentes. Sin embargo, algunas empresas ahora venden productos que permiten la fotoemisión en el aire. La fuente de luz puede ser un láser, un tubo de descarga o una fuente de radiación de sincrotrón . [58]

El analizador hemisférico concéntrico es un analizador de energía de electrones típico. Utiliza un campo eléctrico entre dos hemisferios para cambiar (dispersar) las trayectorias de los electrones incidentes en función de sus energías cinéticas.

Dispositivos de visión nocturna

Los fotones que chocan contra una película delgada de metal alcalino o material semiconductor como el arseniuro de galio en un tubo intensificador de imágenes provocan la expulsión de fotoelectrones debido al efecto fotoeléctrico. Estos son acelerados por un campo electrostático donde chocan contra una pantalla recubierta de fósforo , convirtiendo los electrones nuevamente en fotones. La intensificación de la señal se logra mediante la aceleración de los electrones o aumentando el número de electrones mediante emisiones secundarias, como con una placa de microcanales . A veces se utiliza una combinación de ambos métodos. Se requiere energía cinética adicional para mover un electrón fuera de la banda de conducción y hacia el nivel de vacío. Esto se conoce como la afinidad electrónica del fotocátodo y es otra barrera para la fotoemisión además de la banda prohibida, explicada por el modelo de brecha de banda . Algunos materiales como el arseniuro de galio tienen una afinidad electrónica efectiva que está por debajo del nivel de la banda de conducción. En estos materiales, los electrones que se desplazan hacia la banda de conducción tienen suficiente energía para ser emitidos desde el material, por lo que la película que absorbe los fotones puede ser bastante gruesa. Estos materiales se conocen como materiales de afinidad electrónica negativa. [ cita requerida ]

Astronave

El efecto fotoeléctrico hará que la nave espacial expuesta a la luz solar desarrolle una carga positiva. Esto puede ser un problema importante, ya que otras partes de la nave espacial están en sombra, lo que hará que la nave espacial desarrolle una carga negativa a partir de plasmas cercanos. El desequilibrio puede descargarse a través de componentes eléctricos delicados. La carga estática creada por el efecto fotoeléctrico es autolimitante, porque un objeto con mayor carga no cede sus electrones tan fácilmente como lo hace un objeto con menor carga. [59] [60]

Polvo lunar

La luz del Sol que incide sobre el polvo lunar hace que se cargue positivamente por efecto fotoeléctrico. El polvo cargado se repele y se levanta de la superficie de la Luna por levitación electrostática . [61] [62] Esto se manifiesta casi como una "atmósfera de polvo", visible como una fina neblina y desenfoque de las características distantes, y visible como un brillo tenue después de que el sol se ha puesto. Esto fue fotografiado por primera vez por las sondas del programa Surveyor en la década de 1960, [63] y, más recientemente, el rover Chang'e 3 observó la deposición de polvo en rocas lunares de hasta unos 28 cm de altura. [64] Se cree que las partículas más pequeñas son repelidas a kilómetros de la superficie y que las partículas se mueven en "fuentes" a medida que se cargan y descargan. [65]

Procesos en competencia y sección transversal de fotoemisión

Gráfico de energías de fotones calculadas para un elemento dado (número atómico Z) en el que el valor de la sección transversal para el proceso de la derecha se vuelve mayor que el de la sección transversal para el proceso de la izquierda. Para el calcio (Z=20), la dispersión Compton comienza a predominar en hυ = 0,08 MeV y cesa en 12 MeV. [66]

Cuando las energías de los fotones son tan altas como la energía en reposo del electrón511 keV , puede ocurrir otro proceso, la dispersión Compton . Por encima del doble de esta energía, a1.022 MeV , la producción de pares también es más probable. [67] La ​​dispersión Compton y la producción de pares son ejemplos de otros dos mecanismos en competencia. [ cita requerida ] Incluso si el efecto fotoeléctrico es la reacción favorecida para una interacción particular de un solo fotón con un electrón ligado, el resultado también está sujeto a las estadísticas cuánticas y no está garantizado. La probabilidad de que ocurra el efecto fotoeléctrico se mide por la sección transversal de la interacción, σ. Se ha descubierto que es una función del número atómico del átomo objetivo y la energía del fotón. En una aproximación burda, para energías de fotones superiores a la energía de enlace atómico más alta, la sección transversal viene dada por: [68]

σ = do o norte s a a norte a ⋅ O norte mi 3 {\displaystyle \sigma =\mathrm {constante} \cdot {\frac {Z^{n}}{E^{3}}}}

Aquí Z es el número atómico y n es un número que varía entre 4 y 5. El efecto fotoeléctrico disminuye rápidamente en importancia en la región de rayos gamma del espectro, al aumentar la energía del fotón. También es más probable que se produzca en elementos con un número atómico alto. En consecuencia, los materiales con un valor Z alto son buenos protectores contra los rayos gamma , que es la razón principal por la que se prefiere el plomo ( Z  = 82) y es el más utilizado. [69]

Véase también

Interacción luz-materia
Fenómenos de baja energía:
Efecto fotoeléctrico
Mid-energy phenomena:
Thomson scattering
Compton scattering
High-energy phenomena:
Pair production
Photodisintegration
Photofission

Referencias

  1. ^ 18 de diciembre de 1926: Gilbert Lewis acuña el término "fotón" en una carta a Nature.
  2. ^ "Folleto de datos de rayos X". xdb.lbl.gov . Consultado el 20 de junio de 2020 .
  3. ^ Serway, RA (1990). Física para científicos e ingenieros (3.ª ed.). Saunders . p. 1150. ISBN 0-03-030258-7.
  4. ^ "El efecto fotoeléctrico | Física". courses.lumenlearning.com . Consultado el 8 de julio de 2024 .
  5. ^ ab Lenard, P. (1902). "Ueber die lichtelektrische Wirkung". Annalen der Physik . 313 (5): 149-198. Código bibliográfico : 1902AnP...313..149L. doi : 10.1002/andp.19023130510.
  6. ^ ab Millikan, R. (1914). "Una determinación directa de "h."". Physical Review . 4 (1): 73–75. Código Bibliográfico :1914PhRv....4R..73M. doi :10.1103/PhysRev.4.73.2.
  7. ^ Millikan, R. (1916). "Una determinación fotoeléctrica directa de la "h" de Planck". Physical Review . 7 (3): 355–388. Bibcode :1916PhRv....7..355M. doi : 10.1103/PhysRev.7.355 .
  8. ^ "Analizadores de electrones y fuentes UV de MBScientific".
  9. ^ "Laboratorio Scienta Omicron ARPES".
  10. ^ "Sistema SPECS ARPES con analizador PHOIBOS".
  11. ^ "Sistemas láser Lumeras UV y VUV".
  12. ^ "Fuentes de luz del mundo". 24 de agosto de 2017.
  13. ^ Gautreau, R.; Savin, W. (1999). Esquema de la física moderna de Schaum (2.ª ed.). McGraw-Hill . págs. 60-61. ISBN. 0-07-024830-3.
  14. ^ Zhang, Q. (1996). "Dependencia de la intensidad del efecto fotoeléctrico inducido por un haz de láser polarizado circularmente". Physics Letters A . 216 (1–5): 125. Bibcode :1996PhLA..216..125Z. doi :10.1016/0375-9601(96)00259-9.
  15. ^ Bubb, F. (1924). "Dirección de eyección de fotoelectrones por rayos X polarizados". Physical Review . 23 (2): 137–143. Código Bibliográfico :1924PhRv...23..137B. doi :10.1103/PhysRev.23.137.
  16. ^ Mee, C.; Crundell, M.; Arnold, B.; Brown, W. (2011). Física internacional de nivel A/AS . Hodder Education . pág. 241. ISBN. 978-0-340-94564-3.
  17. ^ Fromhold, AT (1991). Mecánica cuántica para la física aplicada y la ingeniería . Courier Dover Publications . Págs. 5-6. ISBN. 978-0-486-66741-6.
  18. ^ Berglund, CN; Spicer, WE (16 de noviembre de 1964). "Estudios de fotoemisión de cobre y plata: teoría". Physical Review . 136 (4A): A1030–A1044. Código Bibliográfico :1964PhRv..136.1030B. doi :10.1103/PhysRev.136.A1030.
  19. ^ abc Hüfner, S. (2003). Espectroscopia de fotoelectrones: principios y aplicaciones . Springer . ISBN 3-540-41802-4.
  20. ^ Damascelli, Andrea; Shen, Zhi-Xun; Hussain, Zahid (17 de abril de 2003). "Espectroscopia de fotoemisión con resolución angular de los superconductores de cuprato". Reseñas de Física Moderna . 75 (2): 473–541. arXiv : cond-mat/0208504 . doi :10.1103/RevModPhys.75.473. ISSN  0034-6861. S2CID  118433150.
  21. ^ ab Sobota, Jonathan A.; He, Yu; Shen, Zhi-Xun (2021). "Estudios de fotoemisión con resolución angular de materiales cuánticos". Reseñas de Física Moderna . 93 (2): 025006. arXiv : 2008.02378 . Bibcode :2021RvMP...93b5006S. doi :10.1103/RevModPhys.93.025006. S2CID  221006368.
  22. ^ Mahan, GD (1970-12-01). "Teoría de la fotoemisión en metales simples". Physical Review B . 2 (11): 4334–4350. Código Bibliográfico :1970PhRvB...2.4334M. doi :10.1103/PhysRevB.2.4334.
  23. ^ Vesselinka Petrova-Koch; Rudolf Hezel; Adolf Goetzberger (2009). "Hitos de la conversión solar y la energía fotovoltaica". Energía fotovoltaica de bajo costo y alta eficiencia: desarrollos recientes . Springer Series in Optical Sciences. Vol. 140. Springer. pp. 1–. doi :10.1007/978-3-540-79359-5_1. ISBN 978-3-540-79358-8.S2CID108793685  .​
  24. ^ Smith, W. (1873). "Efecto de la luz sobre el selenio durante el paso de una corriente eléctrica". Nature . 7 (173): 303. Bibcode :1873Natur...7R.303.. doi : 10.1038/007303e0 .
  25. ^ Asimov, A. (1964) Enciclopedia biográfica de ciencia y tecnología de Asimov , Doubleday, ISBN 0-385-04693-6 . 
  26. ^ Robert Bud; Deborah Jean Warner (1998). Instruments of Science: An Historical Encyclopedia . Museo de la Ciencia, Londres, y Museo Nacional de Historia Estadounidense, Instituto Smithsoniano. ISBN 978-0-8153-1561-2.
  27. ^ Hertz, Heinrich (1887). "Ueber einen Einfluss des ultravioletten Lichtes auf die electrische Entladung". Annalen der Physik . 267 (8): 983–1000. Código bibliográfico : 1887AnP...267..983H. doi : 10.1002/andp.18872670827.
  28. ^ Hertz, H. (1887). "Ueber sehr schnelle electrische Schwingungen". Annalen der Physik und Chemie . 267 (7): 421–448. Código bibliográfico : 1887AnP...267..421H. doi : 10.1002/andp.18872670707. ISSN  0003-3804.
  29. ^ abc Bloch, Eugene (1914). «Recent developments in electromagnetism» (Desarrollos recientes en electromagnetismo). Informe anual de la Junta de Regentes del Instituto Smithsoniano 1913. Washington, DC: Instituto Smithsoniano. p. 239. Consultado el 2 de mayo de 2020 .
  30. ^ Hallwachs, Wilhelm (1888). "Ueber den Einfluss des Lichtes auf electrostatisch geladene Körper". Annalen der Physik . 269 ​​(2): 301–312. Código bibliográfico : 1888AnP...269..301H. doi : 10.1002/andp.18882690206. ISSN  1521-3889.
  31. ^ Hallwachs, Wied. Ana. xxxiii. pag. 301, 1888.
  32. ^ Hoor, Repertorium des Physik, xxv. pag. 91, 1889.
  33. ^ Bighi, CRcvi. pag. 1349; cvii. pag. 559, 1888
  34. ^ Stoletov. CR cvi. págs. 1149, 1593; cvii. pag. 91; cviii. pag. 1241; Revista Física, Bd. Yo, 1892.
  35. ^ desde
    • Stoletov, A. (1888). "Sur une sorte de courants electriques provoques par les rayons ultraviolets". Cuentas Rendus . CVI : 1149.(Reimpreso en Stoletov, MA (1888). "Sobre una especie de corriente eléctrica producida por rayos ultravioleta". Revista filosófica . Serie 5. 26 (160): 317. doi :10.1080/14786448808628270.; resumen en Beibl. Ana. d. Física. 12, 605, 1888).
    • Stoletov, A. (1888). "Sur les courants actino-electriqies au travers deTair". Cuentas Rendus . CVI : 1593.(Resumen en Beibl. Ann. d. Phys. 12, 723, 1888).
    • Stoletov, A. (1888). "Suite des recherches actino-electriques". Cuentas Rendus . CVII : 91.(Resumen en Beibl. Ann. d. Phys. 12, 723, 1888).
    • Stoletov, A. (1889). "Sur les phénomènes actino-électriques". Cuentas Rendus . CVIII : 1241.
    • Stoletov, A. (1889). "Актино-электрические исследования". Revista de la Sociedad Rusa de Fisicoquímica (en ruso). 21 : 159.
    • Stoletov, A. (1890). "Sur les courants actino-électriques dans l'air raréfié". Revista de físico . 9 : 468. doi : 10.1051/jphystap: 018900090046800.
  36. ^ Hallwachs, W. (1907). "Über die lichtelektrische Ermüdung". Annalen der Physik . 328 (8): 459–516. Código bibliográfico : 1907AnP...328..459H. doi : 10.1002/andp.19073280807.
  37. ^ Schmidt, GC (1898) Wied. Ana. Uiv. pag. 708.
  38. ^ Knoblauch, O. (1899). Zeitschrift für Physikalische Chemie . vol. xxxx. pag. 527.
  39. ^ El Anuario Internacional . (1900). Nueva York: Dodd, Mead & Company. pág. 659.
  40. ^ Historias del electrón: el nacimiento de la microfísica . Buchwald, Jed Z., Warwick, Andrew. Cambridge, Mass.: MIT Press. 2001. ISBN 978-0-262-26948-3.OCLC 62183406  .{{cite book}}: CS1 maint: others (link)
  41. ^ Wheaton, Bruce R. (1978). "Philipp Lenard y el efecto fotoeléctrico, 1889-1911". Estudios históricos en las ciencias físicas . 9 : 299–322. doi :10.2307/27757381. JSTOR  27757381.
  42. ^ Bloch, E. (1908). "La ionización del aire por la luz ultravioleta". El Radio . 5 (8): 240. doi :10.1051/radio:0190800508024001.
  43. ^ Thomson, JJ (1907). "Sobre la ionización de los gases por la luz ultravioleta y sobre la evidencia de la estructura de la luz proporcionada por sus efectos eléctricos". Proc. Camb. Phil. Soc . 14 : 417.
  44. ^ Palmer, Frederic (1908). "Ionización del aire por luz ultravioleta". Nature . 77 (2008): 582. Bibcode :1908Natur..77..582P. doi : 10.1038/077582b0 . S2CID  4028617.
  45. ^ Palmer, Frederic (1911). "Ionización volumétrica producida por luz de longitud de onda extremadamente corta". Physical Review . Serie I. 32 (1): 1–22. Código Bibliográfico :1911PhRvI..32....1P. doi :10.1103/PhysRevSeriesI.32.1.
  46. ^ Planck, Max (1901). "Ueber das Gesetz der Energieverteilung im Normalspectrum (Sobre la ley de distribución de energía en el espectro normal)". Annalen der Physik . 4 (3): 553. Código bibliográfico : 1901AnP...309..553P. doi : 10.1002/andp.19013090310 .
  47. ^ Holton, Gerald (22 de abril de 1999). "Enfoque del centenario: medición de la constante de Planck de Millikan". Física . 3 : 23. doi :10.1103/physrevfocus.3.23.
  48. ^ "El Premio Nobel de Física 1921". Fundación Nobel . Consultado el 9 de octubre de 2008 .
  49. ^ "El Premio Nobel de Física 1923". Fundación Nobel . Consultado el 29 de marzo de 2015 .
  50. ^ Lamb, Willis E. Jr. ; Scully, Marlan O. (1968). "El efecto fotoeléctrico sin fotones" (PDF) . Coral Gables, FL: Centro de Física Teórica, Universidad de Miami. Entendemos el fotoefecto como el resultado de un campo clásico que incide sobre un electrón atómico cuantizado
  51. ^ Einstein, A. "Desde un punto de vista heurístico sobre la emisión y transformación de la luz". Annalen der Physik 17 (1905)
  52. ^ Resnick, Robert (1972) Conceptos básicos de relatividad y teoría cuántica temprana , Wiley, pág. 137, ISBN 0-471-71702-9 . 
  53. ^ ab Knight, Randall D. (2004) Física para científicos e ingenieros con física moderna: un enfoque estratégico , Pearson-Addison-Wesley, pág. 1224, ISBN 0-8053-8685-8 . 
  54. ^ Penrose, Roger (2005) El camino hacia la realidad: una guía completa de las leyes del universo , Knopf, pág. 502, ISBN 0-679-45443-8 
  55. ^ Resnick, Robert (1972) Conceptos básicos de relatividad y teoría cuántica temprana , Wiley, pág. 138, ISBN 0-471-71702-9 . 
  56. ^ Timothy, J. Gethyn (2010) en Huber, Martin CE (ed.) Observación de fotones en el espacio , ISSI Scientific Report 009, ESA Communications, págs. 365-408, ISBN 978-92-9221-938-3 
  57. ^ Burns, RW (1998) Televisión: una historia internacional de los años de formación , IET, pág. 358, ISBN 0-85296-914-7 . 
  58. ^ Weaver, JH; Margaritondo, G. (1979). "Espectroscopia de fotoelectrones de estado sólido con radiación de sincrotrón". Science . 206 (4415): 151–156. Bibcode :1979Sci...206..151W. doi :10.1126/science.206.4415.151. PMID  17801770. S2CID  23594185.
  59. ^ Lai, Shu T. (2011). Fundamentos de la carga de naves espaciales: interacciones de naves espaciales con plasmas espaciales (edición ilustrada). Princeton University Press. pp. 1–6. ISBN 978-0-691-12947-1.
  60. ^ "Carga de nave espacial". Universidad Estatal de Arizona .
  61. ^ Bell, Trudy E., "Fuentes lunares", NASA.gov, 30 de marzo de 2005.
  62. ^ El polvo adquiere carga en el vacío. spacedaily.com, 14 de julio de 2000.
  63. ^ Criswell DR (1973). "El resplandor del horizonte y el movimiento del polvo lunar". En RJL Grard (ed.). Interacciones de fotones y partículas con superficies en el espacio . Sexto simposio de Eslab. Noordwijk, Países Bajos: Springer, Dordrecht. doi :10.1007/978-94-010-2647-5_36.
  64. ^ Yan Q.; Zhang X.; Xie L.; Guo D.; Li Y.; Xu Y.; Xiao Z.; Di K.; Xiao L. (2019). "La misión Chang'E-3 revela una débil actividad de polvo cerca de una superficie geológicamente joven". Geophysical Research Letters . 46 (16): 9405–9413. Código Bibliográfico :2019GeoRL..46.9405Y. doi : 10.1029/2019GL083611 .
  65. ^ Timothy J. Stubbs; Richard R. Vondrak; William M. Farrell (2006). "Un modelo dinámico de fuente para el polvo lunar". Avances en la investigación espacial . 37 (1): 59–66. Bibcode :2006AdSpR..37...59S. doi :10.1016/j.asr.2005.04.048. hdl : 2060/20050175993 . S2CID  56226020.
  66. ^ "XCOM: Base de datos de secciones transversales de fotones". NIST . 17 de septiembre de 2009.
  67. ^ Evans, RD (1955). El núcleo atómico. Malabar, Florida: Krieger. pág. 712. ISBN 0-89874-414-8.
  68. ^ Davisson, CM (1965). "Interacción de la radiación gamma con la materia". En Kai Siegbahn (ed.). Espectroscopia de rayos alfa, beta y gamma: volumen 1. Vol. 1. Ámsterdam: North-Holland Publishing Company. págs. 37–78. Código Bibliográfico :1965abgs.conf...37D.
  69. ^ Knoll, Glenn F. (1999). Detección y medición de la radiación. Nueva York: Wiley. pág. 49. ISBN 0-471-49545-X.
Wikimedia Commons tiene medios relacionados con Efecto fotoeléctrico.
  • Reparto de Astronomía "http://www.astronomycast.com/2014/02/ep-335-photoelectric-effect/". AstronomyCast.
  • Nave, R., " Dualidad onda-partícula ". HyperPhysics.
  • " Efecto fotoeléctrico ". Física 2000. Universidad de Colorado, Boulder, Colorado. (página no encontrada)
  • Grupo ACEPT W3, “ El efecto fotoeléctrico ”. Departamento de Física y Astronomía, Universidad Estatal de Arizona, Tempe, AZ.
  • Haberkern, Thomas y N Deepak " Granos de misticismo: Física cuántica para el profano ". Einstein desmitifica el efecto fotoeléctrico, capítulo 3.
  • Departamento de Física, " El efecto fotoeléctrico Archivado el 1 de agosto de 2009 en Wayback Machine ". Laboratorio de Física 320, Davidson College, Davidson.
  • Fowler, Michael, " El efecto fotoeléctrico ". Física 252, Universidad de Virginia.
  • Vaya a " Acerca de un punto de vista heurístico sobre la emisión y transformación de la luz " para leer una traducción al inglés del artículo de Einstein de 1905. (Consultado: 11 de abril de 2014)
  • http://www.chemistryexplained.com/Ru-Sp/Solar-Cells.html
  • Transductores fotoeléctricos: http://sensorse.com/page4en.html

Subprogramas

  • " Simulador de HTML 5 JavaScript " Proyecto de física de código abierto
  • " Efecto fotoeléctrico ". Proyecto Physics Education Technology (PhET). (Java)
  • Fendt, Walter, " El efecto fotoeléctrico ". (Java)
  • " Applet: Efecto fotográfico Archivado el 14 de marzo de 2010 en Wayback Machine ". Sistema de evaluación y gestión de contenido de aprendizaje distribuido de código abierto. ( Java )
Retrieved from "https://en.wikipedia.org/w/index.php?title=Photoelectric_effect&oldid=1250489592"