Conductividad hidráulica
En ciencia e ingeniería , la conductividad hidráulica ( K , en unidades del SI de metros por segundo), es una propiedad de los materiales porosos , suelos y rocas , que describe la facilidad con la que un fluido (generalmente agua) puede moverse a través del espacio poroso o red de fracturas. [1] Depende de la permeabilidad intrínseca ( k , unidad: m 2 ) del material, el grado de saturación y la densidad y viscosidad del fluido. La conductividad hidráulica saturada, K sat , describe el movimiento del agua a través de medios saturados. Por definición, la conductividad hidráulica es la relación entre el flujo de volumen y el gradiente hidráulico, lo que produce una medida cuantitativa de la capacidad de un suelo saturado para transmitir agua cuando se somete a un gradiente hidráulico.
Métodos de determinación
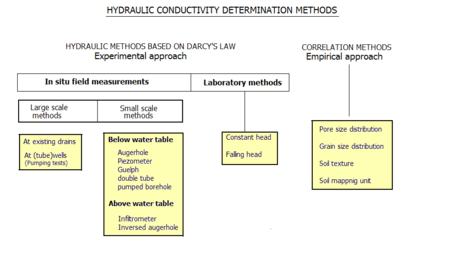
Existen dos enfoques generales para determinar la conductividad hidráulica:
- En el enfoque empírico , la conductividad hidráulica se correlaciona con propiedades del suelo, como las distribuciones de tamaño de poro y tamaño de partícula (tamaño de grano) y la textura del suelo .
- En el enfoque experimental , la conductividad hidráulica se determina a partir de experimentos hidráulicos que se interpretan utilizando la ley de Darcy .
El enfoque experimental se clasifica ampliamente en:
- Pruebas de laboratorio utilizando muestras de suelo sometidas a experimentos hidráulicos
- Pruebas de campo (in situ, on site) que se diferencian en:
- Pruebas de campo a pequeña escala, utilizando observaciones del nivel de agua en cavidades del suelo.
- pruebas de campo a gran escala, como pruebas de bombeo en pozos o mediante la observación del funcionamiento de sistemas de drenaje horizontal existentes.
Las pruebas de campo a pequeña escala se subdividen en:
- Pruebas de infiltración en cavidades por encima del nivel freático
- Pruebas de babosas en cavidades por debajo del nivel freático
Numerosos investigadores investigan los métodos para determinar la conductividad hidráulica y otras propiedades hidráulicas e incluyen enfoques empíricos adicionales. [2]
Estimación mediante un enfoque empírico
Estimación a partir del tamaño del grano
Allen Hazen derivó una fórmula empírica para aproximar la conductividad hidráulica a partir de análisis de tamaño de grano:
dónde
- Coeficiente empírico de Hazen, que toma un valor entre 0,0 y 1,5 (según la literatura), con un valor medio de 1,0. AF Salarashayeri y M. Siosemarde indican que C suele estar entre 1,0 y 1,5, con D en mm y K en cm/s. [ cita requerida ]
- es el diámetro del tamaño de grano del percentil 10 del material.
Función de pedotransferencia
Una función de pedotransferencia (PTF) es un método de estimación empírica especializado, utilizado principalmente en las ciencias del suelo , pero cada vez más utilizado en hidrogeología. [3] Hay muchos métodos de PTF diferentes, sin embargo, todos intentan determinar las propiedades del suelo, como la conductividad hidráulica, dadas varias propiedades del suelo medidas, como el tamaño de partícula del suelo y la densidad aparente .
Determinación mediante enfoque experimental
Existen pruebas de laboratorio relativamente simples y económicas que pueden realizarse para determinar la conductividad hidráulica de un suelo: el método de carga constante y el método de carga descendente.
Métodos de laboratorio
Método de carga constante
El método de carga constante se utiliza normalmente en suelos granulares. Este procedimiento permite que el agua se desplace a través del suelo en condiciones de carga constante mientras se mide el volumen de agua que fluye a través de la muestra de suelo durante un período de tiempo. Conociendo el volumen Δ V de agua medido en un tiempo Δ t , sobre una muestra de longitud L y área de sección transversal A , así como la carga h , se puede derivar la conductividad hidráulica ( K ) simplemente reordenando la ley de Darcy :
Prueba: La ley de Darcy establece que el flujo volumétrico depende de la diferencia de presión Δ P entre los dos lados de la muestra, la permeabilidad k y la viscosidad μ como: [4]
En un experimento de altura constante, la altura (diferencia entre dos alturas) define una masa de agua en exceso, ρAh , donde ρ es la densidad del agua. Esta masa pesa sobre el lado en el que se encuentra, lo que crea una diferencia de presión de Δ P = ρgh , donde g es la aceleración gravitacional. Si introducimos esto directamente en el valor anterior, obtenemos
Si la conductividad hidráulica se define como relacionada con la permeabilidad hidráulica como
Esto da el resultado.
Método de caída de cabeza
En el método de caída de presión, la muestra de suelo se satura primero bajo una condición de presión específica. Luego se permite que el agua fluya a través del suelo sin agregar agua, por lo que la presión de la carga disminuye a medida que el agua pasa a través de la muestra. La ventaja del método de caída de presión es que se puede utilizar tanto para suelos de grano fino como de grano grueso. . [5] Si la presión de la carga disminuye de h i a h f en un tiempo Δ t , entonces la conductividad hidráulica es igual a
Prueba: Como se indicó anteriormente, la ley de Darcy se lee
La disminución del volumen está relacionada con la caída de la carga mediante Δ V = Δ hA . Sustituyendo esta relación en la anterior y tomando el límite como Δ t → 0 , la ecuación diferencial
tiene la solucion
Conectando y reorganizando obtenemos el resultado.
Métodos in situ (de campo)
En comparación con los métodos de laboratorio, los métodos de campo brindan la información más confiable sobre la permeabilidad del suelo con mínimas perturbaciones. En los métodos de laboratorio, el grado de perturbaciones afecta la confiabilidad del valor de la permeabilidad del suelo.
Prueba de bombeo
La prueba de bombeo es el método más confiable para calcular el coeficiente de permeabilidad de un suelo. Esta prueba se clasifica a su vez en prueba de bombeo de entrada y prueba de bombeo de salida.
Método de perforación con barrena
También existen métodos in situ para medir la conductividad hidráulica en el campo.
Cuando el nivel freático es poco profundo, se puede utilizar el método del barreno, una prueba de slug
, para determinar la conductividad hidráulica por debajo del nivel freático.
El método fue desarrollado por Hooghoudt (1934) [6] en los Países Bajos e introducido en los EE. UU. por Van Bavel en Kirkham (1948). [7]
El método utiliza los siguientes pasos:
- Se perfora un agujero en el suelo hasta debajo del nivel freático.
- Se saca agua del barreno
- Se registra la velocidad de subida del nivel del agua en el agujero.
- El valor K se calcula a partir de los datos como: [8]
dónde:
- K es la conductividad hidráulica saturada horizontal (m/día)
- H es la profundidad del nivel del agua en el agujero en relación con el nivel freático en el suelo (cm):
- H t = H en el tiempo t
- H o = H en el tiempo t = 0
- t es el tiempo (en segundos) desde la primera medición de H como H o
- F es un factor que depende de la geometría del agujero:
dónde:
- r es el radio del agujero cilíndrico (cm)
- h' es la profundidad media del nivel del agua en el agujero en relación con el nivel freático en el suelo (cm), que se calcula como
- D es la profundidad del fondo del agujero en relación al nivel freático en el suelo (cm).

La imagen muestra una gran variación de los valores de K medidos con el método del barreno en un área de 100 ha. [9] La relación entre los valores más altos y más bajos es 25. La distribución de frecuencia acumulada es lognormal y se realizó con el programa CumFreq .
Magnitudes relacionadas
Transmisividad
La transmisividad es una medida de cuánta agua se puede transmitir horizontalmente, como por ejemplo a un pozo de bombeo.
- La transmisividad no debe confundirse con la palabra similar transmitancia utilizada en óptica , que significa la fracción de luz incidente que pasa a través de una muestra.
Un acuífero puede estar formado por n capas de suelo. La transmisividad T i de un flujo horizontal para la i- ésima capa de suelo con un espesor saturado d i y una conductividad hidráulica horizontal K i es:
La transmisividad es directamente proporcional a la conductividad hidráulica horizontal K i y al espesor d i . Expresando K i en m/día y d i en m, la transmisividad T i se encuentra en unidades m 2 /día.
La transmisividad total T t del acuífero es la suma de la transmisividad de cada capa: [8]
La conductividad hidráulica horizontal aparente K A del acuífero es:
donde D t , el espesor total del acuífero, es la suma del espesor individual de cada capa:
La transmisividad de un acuífero se puede determinar mediante pruebas de bombeo . [10]
Influencia del nivel freático
Cuando una capa de suelo está por encima del nivel freático , no está saturada y no contribuye a la transmisividad. Cuando la capa de suelo está completamente por debajo del nivel freático, su espesor saturado corresponde al espesor de la propia capa de suelo. Cuando el nivel freático está dentro de una capa de suelo, el espesor saturado corresponde a la distancia del nivel freático hasta el fondo de la capa. Como el nivel freático puede comportarse dinámicamente, este espesor puede cambiar de un lugar a otro o de vez en cuando, de modo que la transmisividad puede variar en consecuencia.
En un acuífero semiconfinado, el nivel freático se encuentra dentro de una capa de suelo con una transmisividad despreciablemente pequeña, de modo que los cambios de la transmisividad total ( D t ) resultantes de los cambios en el nivel del nivel freático son despreciablemente pequeños.
Al bombear agua de un acuífero libre, donde el nivel freático está dentro de una capa de suelo con una transmisividad significativa, el nivel freático puede descender, por lo que la transmisividad se reduce y el flujo de agua al pozo disminuye.
Resistencia
La resistencia al flujo vertical ( R i ) de la i ésima capa de suelo con un espesor saturado d i y conductividad hidráulica vertical K v i es:
Expresando K v i en m/día y d i en m, la resistencia ( R i ) se expresa en días.
La resistencia total ( R t ) del acuífero es la suma de la resistencia de cada capa: [8]
La conductividad hidráulica vertical aparente ( K v A ) del acuífero es:
donde D t es el espesor total del acuífero:
La resistencia juega un papel en los acuíferos donde se presenta una secuencia de capas con permeabilidad horizontal variable de modo que el flujo horizontal se encuentra principalmente en las capas con alta permeabilidad horizontal mientras que las capas con baja permeabilidad horizontal transmiten el agua principalmente en sentido vertical.
Anisotropía
Cuando la conductividad hidráulica horizontal y vertical ( y ) de la capa del suelo difieren considerablemente, se dice que la capa es anisotrópica con respecto a la conductividad hidráulica.
Cuando la conductividad hidráulica horizontal y vertical aparente ( y ) difieren considerablemente, se dice que el acuífero es anisotrópico con respecto a la conductividad hidráulica.
Un acuífero se llama semiconfinado cuando una capa saturada con una conductividad hidráulica horizontal relativamente pequeña (la capa semiconfinante o acuitardo ) se superpone a una capa con una conductividad hidráulica horizontal relativamente alta de modo que el flujo de agua subterránea en la primera capa es principalmente vertical y en la segunda capa principalmente horizontal.
La resistencia de una capa superior semiconfinante de un acuífero se puede determinar a partir de pruebas de bombeo . [10]
Al calcular el flujo a los drenajes [11] o a un campo de pozos [12] en un acuífero con el objetivo de controlar el nivel freático , se debe tener en cuenta la anisotropía, de lo contrario el resultado puede ser erróneo.
Propiedades relativas
Debido a su alta porosidad y permeabilidad, los acuíferos de arena y grava tienen una conductividad hidráulica más alta que los acuíferos de arcilla o granito no fracturado . Por lo tanto, sería más fácil extraer agua de los acuíferos de arena o grava (por ejemplo, mediante un pozo de bombeo ) debido a su alta transmisividad, en comparación con los acuíferos de arcilla o de lecho rocoso no fracturado.
La conductividad hidráulica tiene unidades con dimensiones de longitud por tiempo (por ejemplo, m/s, ft/día y ( gal /día)/ft 2 ); la transmisividad tiene unidades con dimensiones de longitud al cuadrado por tiempo. La siguiente tabla muestra algunos rangos típicos (que ilustran los muchos órdenes de magnitud que son probables) para los valores K.
La conductividad hidráulica ( K ) es una de las propiedades más complejas e importantes de los acuíferos en hidrogeología ya que los valores que se encuentran en la naturaleza son:
- rango de muchos órdenes de magnitud (la distribución a menudo se considera lognormal ),
- varían en gran medida a través del espacio (a veces se considera que están distribuidos espacialmente de manera aleatoria o son de naturaleza estocástica ),
- son direccionales (en general, K es un tensor simétrico de segundo rango ; por ejemplo, los valores de K verticales pueden ser varios órdenes de magnitud más pequeños que los valores de K horizontales ),
- dependen de la escala (probar un m³ de acuífero generalmente producirá resultados diferentes que una prueba similar en solo una muestra de cm³ del mismo acuífero),
- debe determinarse indirectamente a través de pruebas de bombeo de campo , pruebas de flujo de columna de laboratorio o simulación inversa por computadora (a veces también a partir de análisis de tamaño de grano ), y
- son muy dependientes (de manera no lineal ) del contenido de agua, lo que dificulta la resolución de la ecuación de flujo no saturado . De hecho, el K saturado variable para un solo material varía en un rango más amplio que los valores de K saturado para todos los tipos de materiales (consulte el gráfico a continuación para ver un rango ilustrativo de este último).
Rangos de valores para materiales naturales
Tabla de valores de conductividad hidráulica saturada ( K ) encontrados en la naturaleza

Los valores corresponden a condiciones típicas de agua subterránea dulce, utilizando valores estándar de viscosidad y gravedad específica para agua a 20 °C y 1 atm. Consulte la tabla similar derivada de la misma fuente para conocer los valores de permeabilidad intrínseca . [13]
| K (cm/ seg ) | 10² | 10 1 | 10 0 = 1 | 10 −1 | 10 −2 | 10 −3 | 10 −4 | 10 −5 | 10 −6 | 10 −7 | 10 −8 | 10 −9 | 10 −10 |
| K (pies/ día ) | 10 5 | 10.000 | 1.000 | 100 | 10 | 1 | 0,1 | 0,01 | 0,001 | 0,0001 | 10 −5 | 10 −6 | 10 −7 |
| Permeabilidad relativa | Permeable | Semipermeable | Impermeable | ||||||||||
| Acuífero | Bien | Pobre | Ninguno | ||||||||||
| Arena y grava no consolidadas | Grava bien clasificada | Arena bien clasificada o arena y grava | Arena muy fina, limo, loess , marga | ||||||||||
| Arcilla no consolidada y orgánica | Turba | Arcilla en capas | Arcilla grasa/no meteorizada | ||||||||||
| Rocas consolidadas | Rocas altamente fracturadas | Rocas en los yacimientos de petróleo | Arenisca fresca | Caliza fresca , dolomita | Granito fresco | ||||||||
Fuente: modificado de Bear, 1972
| Tipo de suelo | Límite líquido, LL (%) | Relación de vacío en el límite líquido, (%) | Conductividad hidráulica, cm/s |
|---|---|---|---|
| Bentonita | 330 | 9.24 | 1,28 |
| Arena de bentonita | 215 | 5,91 | 2,65 |
| Suelo marino natural | 106 | 2.798 | 2,56 |
| Suelo marino secado al aire | 84 | 2.234 | 2,42 |
| Suelo marino secado al aire libre | 60 | 1.644 | 2,63 |
| Suelo pardo | 62 | 1.674 | 2,83 |
Véase también
- Prueba de acuífero
- Analogía hidráulica
- Función de pedotransferencia : para estimar conductividades hidráulicas dadas las propiedades del suelo
Referencias
- ^ https://www.preene.com/blog/2014/07/what-is-hydraulic-conductivity#:~:text=DEFINICIONES%20DE%20CONDUCTIVIDAD%20HIDRÁULICA&text=En%20términos%20teóricos%20de%20conductividad%20hidráulica,el%20material%20es%20menos%20permeable. Definición de conductividad hidráulica
- ^ Sahu, Sudarsan; Saha, Dipankar (2016). "Métodos empíricos y estimación de la conductividad hidráulica de los acuíferos fluviales". Environmental & Engineering Geoscience . 22 (4): 319–340. Bibcode :2016EEGeo..22..319S. doi :10.2113/gseegeosci.22.4.319.
- ^ Wösten, JHM, Pachepsky, YA y Rawls, WJ (2001). "Funciones de pedotransferencia: cerrando la brecha entre los datos básicos del suelo disponibles y las características hidráulicas del suelo faltantes". Journal of Hydrology . 251 (3–4): 123–150. Bibcode :2001JHyd..251..123W. doi :10.1016/S0022-1694(01)00464-4.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Control del flujo capilar: una aplicación de la ley de Darcy
- ^ Liu, Cheng "Suelos y cimientos". Upper Saddle River, Nueva Jersey: Prentice Hall, 2001 ISBN 0-13-025517-3
- ^ SBHooghoudt, 1934, en holandés. Bijdrage tot de kennis van enige natuurkundige grootheden van de grond. Verslagen Landbouwkundig Onderzoek n° 40 B, pág. 215-345.
- ^ CHM van Bavel y D. Kirkham, 1948. Medición de campo de la permeabilidad del suelo mediante perforaciones con barrena. Soil. Sci. Soc. Am. Proc 13:90-96.
- ^ abc Determinación de la conductividad hidráulica saturada. Capítulo 12 en: HPRitzema (ed., 1994) Principios y aplicaciones del drenaje, ILRI Publication 16, págs. 435-476. Instituto Internacional de Recuperación y Mejora de Tierras, Wageningen (ILRI), Países Bajos. ISBN 90-70754-33-9 . Descarga gratuita desde: [1], bajo el n.° 6, o directamente como PDF: [2]
- ^ Investigación sobre drenaje en campos de agricultores: análisis de datos. Contribución al proyecto “Oro líquido” del Instituto Internacional para la Recuperación y Mejora de Tierras (ILRI), Wageningen, Países Bajos. Descarga gratuita desde: [3], en el n.° 2, o directamente como PDF: [4]
- ^ ab J.Boonstra y RALKselik, SATEM 2002: Software para la evaluación de pruebas de acuíferos, 2001. Publ. 57, Instituto Internacional para la Recuperación y Mejora de Tierras (ILRI), Wageningen, Países Bajos. ISBN 90-70754-54-1 En línea : [5]
- ^ Balance energético del flujo de agua subterránea aplicado al drenaje subterráneo en suelos anisotrópicos mediante tuberías o zanjas con resistencia de entrada. Instituto Internacional de Recuperación y Mejora de Tierras, Wageningen, Países Bajos. En línea: [6] Archivado el 19 de febrero de 2009 en Wayback Machine . Artículo basado en: RJ Oosterbaan, J. Boonstra y KVGK Rao, 1996, “El balance energético del flujo de agua subterránea”. Publicado en VPSingh y B.Kumar (eds.), Subsurface-Water Hydrology, pág. 153-160, Vol.2 de Proceedings of the International Conference on Hydrology and Water Resources, Nueva Delhi, India, 1993. Kluwer Academic Publishers, Dordrecht, Países Bajos. ISBN 978-0-7923-3651-8 . En línea: [7]. El programa gratuito EnDrain correspondiente se puede descargar desde: [8]
- ^ Drenaje subterráneo mediante pozos (tubulares), 9 pp. Explicación de las ecuaciones utilizadas en el modelo WellDrain. Instituto Internacional para la Recuperación y Mejora de Tierras (ILRI), Wageningen, Países Bajos. En línea: [9]. El programa WellDrain correspondiente se puede descargar de forma gratuita desde: [10]
- ^ Bear, J. (1972). Dinámica de fluidos en medios porosos . Publicaciones de Dover . ISBN. 0-486-65675-6.
- ^ Tabla 4.4 James K. Mitchell, Kenichi Soga, Fundamentals of SoilBehavior, tercera ed., John Wiley & Sons Inc., Hoboken, NJ, 2005, 577 pp., ISBN 0-471-46302-7.
- ^ Nagaraj, TS, Pandian, NS y Narasimha Raju, PSR 1991. Un enfoque para la predicción del comportamiento de compresibilidad y permeabilidad de mezclas de arena y bentonita, Indian Geotechnical Journal, vol. 21, n.º 3, págs. 271-282
Enlaces externos
- Calculadora de conductividad hidráulica





























