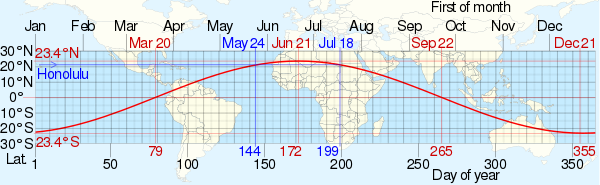
Angulo cenital solar

El ángulo cenital solar es el ángulo cenital del sol , es decir, el ángulo entre los rayos solares y la dirección vertical . Es el complemento de la altitud solar o elevación solar , que es el ángulo de altitud o ángulo de elevación entre los rayos solares y un plano horizontal . ^{[1] [2]} Al mediodía solar , el ángulo cenital está en un mínimo y es igual a la latitud menos el ángulo de declinación solar . Esta es la base por la que los antiguos marineros navegaban por los océanos. ^[3]

El ángulo cenital solar se utiliza normalmente en combinación con el ángulo azimutal solar para determinar la posición del Sol observada desde una ubicación determinada en la superficie de la Tierra.

$${\displaystyle \cos \theta _ {s}=\sin \alpha _ {s}=\sin \Phi \sin \delta +\cos \Phi \cos \delta \cos h}$$

dónde

• ${\displaystyle \theta_{s}}$¿Es el ángulo cenital solar?
• ${\displaystyle \alpha _{s}}$es el ángulo de altitud solar ,${\displaystyle \alpha _{s}=90^{\circ }-\theta _{s}}$
• ${\estilo de visualización h}$es el ángulo horario , en la hora solar local .
• ${\estilo de visualización \delta}$es la declinación actual del Sol
• ${\estilo de visualización \Phi}$es la latitud local .

Si bien la fórmula se puede derivar aplicando la ley del coseno al triángulo esférico formado por el polo cenit y el Sol, la trigonometría esférica es un tema relativamente esotérico.

Introduciendo las coordenadas del punto subsolar y utilizando el análisis vectorial, la fórmula se puede obtener de forma sencilla sin tener que recurrir a la trigonometría esférica. ^[4]

En el sistema de coordenadas cartesianas geocéntricas Tierra-Fija ( ECEF ), sean y las latitudes y longitudes, o coordenadas, del punto subsolar y el punto del observador, entonces los vectores unitarios que apuntan hacia arriba en los dos puntos, y , son${\displaystyle (\phi _{s},\lambda _{s})}$${\displaystyle (\phi _ {o},\lambda _ {o})}$${\displaystyle \mathbf {S}}$${\displaystyle \mathbf {V} _ {oz}}$

$${\displaystyle \mathbf {S} =\cos \phi _{s}\cos \lambda _{s}{\mathbf {i} }+\cos \phi _{s}\sin \lambda _{s}{ \mathbf {j} }+\sin \phi _ {s}{\mathbf {k} },}$$$${\displaystyle \mathbf {V} _{oz}=\cos \phi _{o}\cos \lambda _{o}{\mathbf {i} }+\cos \phi _{o}\sin \lambda _ {o}{\mathbf {j} }+\sin \phi _{o}{\mathbf {k} }.}$$

donde , y son los vectores base en el sistema de coordenadas ECEF.${\displaystyle {\mathbf {i}}$${\displaystyle {\mathbf {j} }}$${\displaystyle {\mathbf {k}}$

Ahora bien, el coseno del ángulo cenital solar, , es simplemente el producto escalar de los dos vectores anteriores.${\displaystyle \theta_{s}}$

$${\displaystyle \cos \theta _ {s}=\mathbf {S} \cdot \mathbf {V} _ {oz}=\sin \phi _ {o}\sin \phi _ {s}+\cos \phi _{o}\cos \phi _{s}\cos(\lambda _{s}-\lambda _{o}).}$$

Tenga en cuenta que es lo mismo que , la declinación del Sol, y es equivalente a , donde es el ángulo horario definido anteriormente. Por lo tanto, el formato anterior es matemáticamente idéntico al que se proporcionó anteriormente. ${\displaystyle \phi_{s}}$${\estilo de visualización \delta}$${\displaystyle \lambda_{s}-\lambda_{o}}$${\estilo de visualización -h}$${\estilo de visualización h}$

Además, la referencia ^[4] también derivó la fórmula para el ángulo azimutal solar de manera similar sin utilizar trigonometría esférica.

En cualquier lugar y día, el ángulo cenital solar, , alcanza su mínimo, , al mediodía solar local cuando el ángulo horario , o , es decir, , o . Si , es noche polar.${\displaystyle \theta_{s}}$${\displaystyle \theta _{\text{mín}}}$${\estilo de visualización h=0}$${\displaystyle \lambda_{s}-\lambda_{o}=0}$${\displaystyle \cos \theta _{\text{mín}}=\cos(|\phi _{o}-\phi _{s}|)}$${\displaystyle \theta _{\text{min}}=|\phi _{o}-\phi _{s}|}$${\displaystyle \theta _{\text{mín}}>90^{\circ }}$

Y en cualquier lugar dado en cualquier día dado, el ángulo cenital solar, , alcanza su máximo, , a la medianoche local cuando el ángulo horario , o , es decir, , o . Si , es día polar.${\displaystyle \theta_{s}}$${\displaystyle \theta _ {\text{máx}}}$${\displaystyle h=-180^{\circ }}$${\displaystyle \lambda_{s}-\lambda_{o}=-180^{\circ }}$${\displaystyle \cos \theta _{\text{máx}}=\cos(180^{\circ }-|\phi _{o}+\phi _{s}|)}$${\displaystyle \theta _{\text{máx}}=180^{\circ }-|\phi _{o}+\phi _{s}|}$${\displaystyle \theta _{\text{máx}}<90^{\circ }}$

Los valores calculados son aproximaciones debido a la distinción entre latitud común/geodésica y latitud geocéntrica . Sin embargo, los dos valores difieren en menos de 12 minutos de arco , que es menor que el radio angular aparente del sol.

La fórmula también tiene en cuenta el efecto de la refracción atmosférica . ^[5]

La puesta y la salida del sol se producen (aproximadamente) cuando el ángulo cenital es de 90°, donde el ángulo horario h ₀ satisface ^[2]$${\displaystyle \cos h_{0}=-\tan \Phi \tan \delta .}$$

Los momentos precisos del amanecer y el atardecer ocurren cuando el extremo superior del Sol aparece, refractado por la atmósfera, en el horizonte.

Un ángulo cenital promedio diario ponderado, utilizado para calcular el albedo local de la Tierra , se da por donde Q es la irradiancia instantánea . ^[2]$${\displaystyle {\overline {\cos \theta _{s}}}={\frac {\displaystyle \int _{-h_{0}}^{h_{0}}Q\cos \theta _{s}\,{\text{d}}h}{\displaystyle \int _{-h_{0}}^{h_{0}}Q\,{\text{d}}h}}}$$

Por ejemplo, el ángulo de elevación solar es:

• 90° si estás en el ecuador, un día de equinoccio, a la hora solar de doce
• cerca de 0° al atardecer o al amanecer
• Entre −90° y 0° durante la noche (medianoche)

En la posición del Sol se da un cálculo exacto . Existen otras aproximaciones en otros lugares. ^[6]

Fechas aproximadas de puntos subsolares vs latitud superpuestas en un mapa mundial, el ejemplo en azul indica el mediodía de Lahaina en Honolulu

• Azimut
• Ángulo azimutal solar
• Sistema de coordenadas horizontales
• Lista de órbitas
• Sistema de montaje fotovoltaico § Orientación e inclinación
• Posición del sol
• Camino del sol
• Amanecer
• Atardecer
• Tiempo de tránsito del sol