Óptica de índice de gradiente

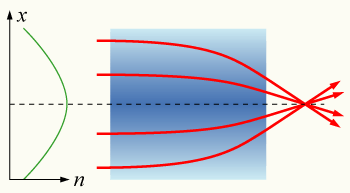
La óptica de índice de gradiente ( GRIN ) es la rama de la óptica que abarca los efectos ópticos producidos por un gradiente del índice de refracción de un material. Dicha variación gradual se puede utilizar para producir lentes con superficies planas o lentes que no tengan las aberraciones típicas de las lentes esféricas tradicionales. Las lentes de índice de gradiente pueden tener un gradiente de refracción esférico, axial o radial.

El cristalino del ojo es el ejemplo más obvio de óptica de índice de gradiente en la naturaleza. En el ojo humano , el índice de refracción del cristalino varía desde aproximadamente 1,406 en las capas centrales hasta 1,386 en las capas menos densas del cristalino. ^[1] Esto permite al ojo tomar imágenes con buena resolución y baja aberración tanto a distancias cortas como largas. ^[2]

Otro ejemplo de la óptica del índice de gradiente en la naturaleza es el espejismo común de un charco de agua que aparece en una carretera en un día caluroso. El charco es en realidad una imagen del cielo, aparentemente ubicada en la carretera, ya que los rayos de luz se refractan (desvían) de su trayectoria recta normal. Esto se debe a la variación del índice de refracción entre el aire caliente y menos denso en la superficie de la carretera y el aire frío y más denso que se encuentra sobre ella. La variación de la temperatura (y, por lo tanto, la densidad) del aire provoca un gradiente en su índice de refracción, lo que hace que aumente con la altura. ^[3] Este gradiente del índice provoca la refracción de los rayos de luz (en un ángulo poco profundo con respecto a la carretera) desde el cielo, desviándolos hacia el ojo del observador, siendo su ubicación aparente la superficie de la carretera.

La atmósfera de la Tierra actúa como una lente GRIN, permitiendo a los observadores ver el sol durante unos minutos después de que esté realmente debajo del horizonte, y los observadores también pueden ver estrellas que están debajo del horizonte. ^[3] Este efecto también permite la observación de señales electromagnéticas de los satélites después de que hayan descendido por debajo del horizonte, como en las mediciones de ocultación de radio .

La capacidad de las lentes GRIN de tener superficies planas simplifica el montaje de la lente, lo que las hace útiles donde se necesitan montar juntas muchas lentes muy pequeñas, como en fotocopiadoras y escáneres . ^[4] La superficie plana también permite que una lente GRIN se alinee ópticamente fácilmente con una fibra , para producir una salida colimada , lo que la hace aplicable para la endoscopia , así como para la obtención de imágenes de calcio in vivo y la estimulación optogenética en el cerebro. ^[5]

En aplicaciones de imagen, las lentes GRIN se utilizan principalmente para reducir las aberraciones. El diseño de dichas lentes implica cálculos detallados de las aberraciones, así como una fabricación eficiente de las lentes. Se han utilizado varios materiales diferentes para las lentes GRIN, incluidos vidrios ópticos, plásticos, germanio , seleniuro de zinc y cloruro de sodio . ^[4]

Ciertas fibras ópticas ( fibras de índice graduado ) están hechas con un perfil de índice de refracción que varía radialmente; este diseño reduce fuertemente la dispersión modal de una fibra óptica multimodo . La variación radial en el índice de refracción permite una distribución de altura sinusoidal de los rayos dentro de la fibra, evitando que los rayos salgan del núcleo . Esto difiere de las fibras ópticas tradicionales, que dependen de la reflexión interna total , en que todos los modos de las fibras GRIN se propagan a la misma velocidad, lo que permite un mayor ancho de banda temporal para la fibra. ^[6]

Los recubrimientos antirreflejos suelen ser eficaces para rangos estrechos de frecuencia o ángulo de incidencia. Los materiales de índice graduado están menos restringidos. ^[7]

Se ha utilizado una lente de gradiente axial para concentrar la luz solar en las células solares, capturando hasta el 90% de la luz incidente cuando el sol no está en un ángulo óptimo. ^[8]

Las lentes GRIN se fabrican mediante varias técnicas:

• Irradiación de neutrones : el vidrio rico en boro se bombardea con neutrones para provocar un cambio en la concentración de boro y, por lo tanto, en el índice de refracción de la lente. ^{[6] [9]}
• Deposición química en fase de vapor : consiste en depositar distintos vidrios con distintos índices de refracción sobre una superficie para producir un cambio de refracción acumulativo. ^{[6] [10]}
• Polimerización parcial : un monómero orgánico se polimeriza parcialmente utilizando luz ultravioleta a distintas intensidades para generar un gradiente de refracción. ^{[6] [11]}
• Intercambio iónico : el vidrio se sumerge en una masa líquida con iones de litio . Como resultado de la difusión , los iones de sodio del vidrio se intercambian parcialmente con los de litio, y la mayor cantidad de intercambio se produce en el borde. De este modo, la muestra obtiene una estructura de material en gradiente y un gradiente correspondiente del índice de refracción. ^{[6] [12]}
• Relleno de iones: la separación de fases de un vidrio específico hace que se formen poros, que luego pueden rellenarse utilizando una variedad de sales o concentraciones de sales para dar un gradiente variable. ^{[6] [13]}
• Escritura láser directa : mientras se expone punto por punto la estructura prediseñada, se varía la dosis de exposición (velocidad de escaneo, potencia del láser, etc.). Esto corresponde a un grado de conversión de monómero a polímero ajustable espacialmente, lo que da como resultado un índice de refracción diferente. El método es aplicable a elementos microópticos de forma libre y a ópticas multicomponentes. ^[14]

En 1854, JC Maxwell sugirió una lente cuya distribución del índice de refracción permitiría obtener imágenes nítidas de cada región del espacio. Conocida como la lente ojo de pez de Maxwell , implica una función de índice esférico y se esperaría que también tuviera forma esférica. ^[15] Sin embargo, esta lente es poco práctica de fabricar y tiene poca utilidad, ya que solo se obtienen imágenes nítidas de los puntos de la superficie y dentro de la lente y los objetos extendidos sufren aberraciones extremas. En 1905, RW Wood utilizó una técnica de inmersión para crear un cilindro de gelatina con un gradiente de índice de refracción que variaba simétricamente con la distancia radial desde el eje. Más tarde se demostró que las rebanadas en forma de disco del cilindro tenían caras planas con distribución de índice radial. Demostró que, aunque las caras de la lente eran planas, actuaban como lentes convergentes y divergentes dependiendo de si el índice era decreciente o creciente en relación con la distancia radial. ^[16] En 1964, se publicó un libro póstumo de RK Luneburg en el que describía una lente que enfoca rayos de luz paralelos incidentes sobre un punto en la superficie opuesta de la lente. ^[17] Esto también limitó las aplicaciones de la lente porque era difícil usarla para enfocar la luz visible; sin embargo, tenía cierta utilidad en aplicaciones de microondas . Algunos años después se han desarrollado varias técnicas nuevas para fabricar lentes del tipo Wood. Desde entonces, al menos las lentes GRIN más delgadas pueden poseer propiedades de imagen sorprendentemente buenas considerando su construcción mecánica muy simple, mientras que las lentes GRIN más gruesas encontraron aplicación, por ejemplo, en las varillas Selfoc . ^[18]

Una lente de índice de gradiente no homogéneo posee un índice de refracción cuyo cambio sigue la función de las coordenadas de la región de interés en el medio. Según el principio de Fermat , la integral de la trayectoria de la luz ( L ), tomada a lo largo de un rayo de luz que une dos puntos cualesquiera de un medio , es estacionaria en relación con su valor para cualquier curva cercana que una los dos puntos. La integral de la trayectoria de la luz está dada por la ecuación${\displaystyle n=f(x,y,z)}$

${\displaystyle L=\int _{S_{o}}^{S}n\,ds}$, donde n es el índice de refracción y S es la longitud del arco de la curva. Si se utilizan coordenadas cartesianas , esta ecuación se modifica para incorporar el cambio en la longitud del arco para un gradiente esférico, a cada dimensión física:

${\displaystyle L=\int _{S_{o}}^{S}n(x,y,z){\sqrt {x'^{2}+y'^{2}+z'^{2}}}\,ds}$

donde primo corresponde a d/d s. ^[19] La integral de trayectoria de la luz es capaz de caracterizar la trayectoria de la luz a través de la lente de una manera cualitativa, de tal manera que la lente pueda reproducirse fácilmente en el futuro.

El gradiente del índice de refracción de las lentes GRIN se puede modelar matemáticamente según el método de producción utilizado. Por ejemplo, las lentes GRIN fabricadas a partir de un material con índice de gradiente radial, como las microlentes SELFOC ^[20] , tienen un índice de refracción que varía según:

${\displaystyle n_{r}=n_{o}\left(1-{\frac {Ar^{2}}{2}}\right)}$, donde n _r es el índice de refracción a una distancia, r , del eje óptico ; n _o es el índice de diseño en el eje óptico y A es una constante positiva.

• Fibra de índice graduado