Operación bit a bit
This article needs additional citations for verification. (August 2018) |
En programación informática , una operación bit a bit opera sobre una cadena de bits , una matriz de bits o un numeral binario (considerado como una cadena de bits) a nivel de sus bits individuales . Es una acción rápida y sencilla, básica para las operaciones aritméticas de nivel superior y directamente soportada por el procesador . La mayoría de las operaciones bit a bit se presentan como instrucciones de dos operandos donde el resultado reemplaza a uno de los operandos de entrada.
En procesadores simples y de bajo costo, por lo general, las operaciones bit a bit son sustancialmente más rápidas que la división, varias veces más rápidas que la multiplicación y, a veces, significativamente más rápidas que la suma. Si bien los procesadores modernos suelen realizar la suma y la multiplicación con la misma rapidez que las operaciones bit a bit debido a sus secuencias de instrucciones más largas y otras opciones de diseño arquitectónico , las operaciones bit a bit suelen consumir menos energía debido al uso reducido de recursos. [1]
Operadores bit a bit
En las explicaciones que se dan a continuación, cualquier indicación de la posición de un bit se cuenta desde el lado derecho (el menos significativo), avanzando hacia la izquierda. Por ejemplo, el valor binario 0001 (1 decimal) tiene ceros en todas las posiciones excepto en la primera (es decir, la más a la derecha).
NO
El NOT bit a bit , o complemento bit a bit , es una operación unaria que realiza una negación lógica en cada bit, formando el complemento a uno del valor binario dado. Los bits que son 0 se convierten en 1 y los que son 1 se convierten en 0. Por ejemplo:
NO 0 111 (decimal 7) = 1 000 (decimal 8)
NO 10101011 (decimal 171) = 01010100 (decimal 84)
El resultado es igual al complemento a dos del valor menos uno. Si se utiliza la aritmética del complemento a dos, entonces NOT x = -x − 1.
En el caso de los números enteros sin signo , el complemento bit a bit de un número es el "reflejo especular" del número en el punto medio del rango del número entero sin signo. Por ejemplo, en el caso de los números enteros sin signo de 8 bits, NOT x = 255 - x, que se puede visualizar en un gráfico como una línea descendente que "invierte" efectivamente un rango creciente de 0 a 255 a un rango decreciente de 255 a 0. Un ejemplo de uso simple pero ilustrativo es invertir una imagen en escala de grises donde cada píxel se almacena como un número entero sin signo.
Y

Una operación AND bit a bit es una operación binaria que toma dos representaciones binarias de igual longitud y realiza la operación AND lógica en cada par de bits correspondientes. Por lo tanto, si ambos bits en la posición comparada son 1, el bit en la representación binaria resultante es 1 (1 × 1 = 1); de lo contrario, el resultado es 0 (1 × 0 = 0 y 0 × 0 = 0). Por ejemplo:
010 1 (decimal 5)Y 001 1 (decimal 3) = 000 1 (decimal 1)
La operación se puede utilizar para determinar si un bit en particular está activado (1) o desactivado (0). Por ejemplo, dado un patrón de bits 0011 (decimal 3), para determinar si el segundo bit está activado, utilizamos un AND bit a bit con un patrón de bits que contiene 1 solo en el segundo bit:
00 1 1 (decimal 3)Y 00 1 0 (decimal 2) = 00 1 0 (decimal 2)
Como el resultado 0010 no es cero, sabemos que se configuró el segundo bit del patrón original. Esto se suele denominar enmascaramiento de bits . (Por analogía, el uso de cinta adhesiva cubre o enmascara partes que no se deben alterar o partes que no son de interés. En este caso, los valores 0 enmascaran los bits que no son de interés).
El AND bit a bit se puede utilizar para borrar bits seleccionados (o indicadores ) de un registro en el que cada bit representa un estado booleano individual . Esta técnica es una forma eficiente de almacenar una cantidad de valores booleanos utilizando la menor cantidad de memoria posible.
Por ejemplo, 0110 (decimal 6) puede considerarse un conjunto de cuatro indicadores numerados de derecha a izquierda, donde el primero y el cuarto indicadores están desactivados (0), y el segundo y el tercero están activados (1). El tercer indicador puede desactivarse mediante un AND bit a bit con el patrón que tiene un cero solo en el tercer bit:
0 1 10 (decimal 6)Y 1 0 11 (decimal 11) = 0 0 10 (decimal 2)
Gracias a esta propiedad, resulta fácil comprobar la paridad de un número binario comprobando el valor del bit de menor valor. Utilizando el ejemplo anterior:
0110 (decimal 6)Y 0001 (decimal 1) = 0000 (decimal 0)
Como 6 Y 1 es cero, 6 es divisible por dos y, por lo tanto, par.
O

Un OR bit a bit es una operación binaria que toma dos patrones de bits de igual longitud y realiza la operación OR lógica inclusiva en cada par de bits correspondientes. El resultado en cada posición es 0 si ambos bits son 0, mientras que en caso contrario el resultado es 1. Por ejemplo:
0 101 (decimal 5)O 0 011 (decimal 3) = 0 111 (decimal 7)
El OR bit a bit se puede utilizar para poner a 1 los bits seleccionados del registro descrito anteriormente. Por ejemplo, el cuarto bit de 0010 (decimal 2) se puede poner a 1 realizando un OR bit a bit con el patrón con solo el cuarto bit puesto:
0 0 1 0 (decimal 2)O 1 0 0 0 (decimal 8) = 1 0 1 0 (decimal 10)
O-X

Un XOR bit a bit es una operación binaria que toma dos patrones de bits de igual longitud y realiza la operación lógica OR exclusiva sobre cada par de bits correspondientes. El resultado en cada posición es 1 si solo uno de los bits es 1, pero será 0 si ambos son 0 o ambos son 1. En esta realizamos la comparación de dos bits, siendo 1 si los dos bits son diferentes, y 0 si son iguales. Por ejemplo:
0 10 1 (decimal 5)XOR 0 01 1 (decimal 3) = 0 11 0 (decimal 6)
La operación XOR a nivel de bit se puede utilizar para invertir los bits seleccionados en un registro (también se denomina alternar o invertir). Cualquier bit se puede alternar mediante la operación XOR con 1. Por ejemplo, dado el patrón de bits 0010 (decimal 2), el segundo y el cuarto bit se pueden alternar mediante una operación XOR a nivel de bit con un patrón de bits que contenga 1 en la segunda y cuarta posición:
0 0 1 0 (decimal 2)XOR 1 0 1 0 (decimal 10) = 1 0 0 0 (decimal 8)
Esta técnica se puede utilizar para manipular patrones de bits que representan conjuntos de estados booleanos.
Los programadores de lenguaje ensamblador y los compiladores optimizadores a veces usan XOR como un atajo para establecer el valor de un registro en cero. Realizar XOR sobre un valor contra sí mismo siempre da como resultado cero y, en muchas arquitecturas, esta operación requiere menos ciclos de reloj y menos memoria que cargar un valor cero y guardarlo en el registro.
Si el conjunto de cadenas de bits de longitud fija n (es decir, palabras de máquina ) se considera como un espacio vectorial de n dimensiones sobre el campo , entonces la suma de vectores corresponde al XOR bit a bit.
Equivalentes matemáticos
Suponiendo que , para los números enteros no negativos, las operaciones bit a bit se pueden escribir de la siguiente manera:
Tabla de verdad para todos los operadores lógicos binarios
Hay 16 funciones de verdad posibles de dos variables binarias ; esto define una tabla de verdad .
Aquí están las operaciones equivalentes bit a bit de dos bits P y Q:
| pag | q | O 0 | NORTE 1 | Xq 2 | ¬pág . 3 | ↛ 4 | ¬q 5 | O-X 6 | NAND 7 | Y 8 | XNOR9 | q 10 | Si/entonces 11 | pág. 12 | Entonces/si 13 | O 14 | T15 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | ||
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | ||
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | ||
Equivalentes bit a bit | 0 | NO (p O q) | (NO p) Y q | NO p | p Y (NO q) | NO q | p XOR q | NO (p Y q) | p y q | NO (p XOR q) | q | (NO p) O q | pag | p O (NO q) | p o q | 1 | |||
Cambios de bits
Los desplazamientos de bits a veces se consideran operaciones bit a bit, porque tratan un valor como una serie de bits en lugar de como una cantidad numérica. En estas operaciones, los dígitos se mueven, o desplazan , hacia la izquierda o la derecha. Los registros de un procesador de computadora tienen un ancho fijo, por lo que algunos bits se "desplazarán hacia afuera" del registro en un extremo, mientras que la misma cantidad de bits se "desplazarán hacia adentro" desde el otro extremo; las diferencias entre los operadores de desplazamiento de bits radican en cómo determinan los valores de los bits desplazados hacia adentro.
Direccionamiento de bits
Si el ancho del registro (con frecuencia 32 o incluso 64) es mayor que el número de bits (normalmente 8) de la unidad direccionable más pequeña, frecuentemente llamada byte, las operaciones de desplazamiento inducen un esquema de direccionamiento de los bytes a los bits. De este modo, las orientaciones "izquierda" y "derecha" se toman de la escritura estándar de números en una notación de valor posicional , de modo que un desplazamiento a la izquierda aumenta y un desplazamiento a la derecha disminuye el valor del número ―si los dígitos de la izquierda se leen primero, esto constituye una orientación big-endian . Sin tener en cuenta los efectos de límite en ambos extremos del registro, las operaciones de desplazamiento aritmético y lógico se comportan de la misma manera, y un desplazamiento de 8 posiciones de bit transporta el patrón de bits en 1 posición de byte de la siguiente manera:
Ordenamiento little-endian : Un desplazamiento a la izquierda de 8 posiciones aumenta la dirección del byte en 1, Un desplazamiento a la derecha de 8 posiciones disminuye la dirección del byte en 1. Ordenación big-endian : un desplazamiento a la izquierda de 8 posiciones disminuye la dirección del byte en 1, Un desplazamiento a la derecha de 8 posiciones aumenta la dirección del byte en 1.
Desplazamiento aritmético

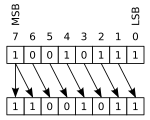
En un desplazamiento aritmético , los bits que se desplazan hacia afuera de cualquiera de los extremos se descartan. En un desplazamiento aritmético hacia la izquierda, los ceros se desplazan hacia adentro a la derecha; en un desplazamiento aritmético hacia la derecha, el bit de signo (el MSB en complemento a dos) se desplaza hacia adentro a la izquierda, preservando así el signo del operando.
Este ejemplo utiliza un registro de 8 bits, interpretado como complemento a dos:
00010111 (decimal +23) MAYÚS IZQUIERDA= 0010111 0 (decimal +46)
10010111 (decimal −105) DESPLAZAMIENTO A LA DERECHA= 1 1001011 (decimal -53)
En el primer caso, el dígito más a la izquierda se desplazó más allá del final del registro y se desplazó un nuevo 0 a la posición más a la derecha. En el segundo caso, el 1 más a la derecha se desplazó hacia afuera (quizás hacia la bandera de acarreo ) y se copió un nuevo 1 en la posición más a la izquierda, preservando el signo del número. Los desplazamientos múltiples a veces se acortan a un solo desplazamiento por una cierta cantidad de dígitos. Por ejemplo:
00010111 (decimal +23) MAYÚS IZQUIERDA DE DOS EN DOS= 010111 00 (decimal +92)
Un desplazamiento aritmético hacia la izquierda en n equivale a multiplicar por 2 n (siempre que el valor no se desborde ), mientras que un desplazamiento aritmético hacia la derecha en n de un valor de complemento a dos equivale a tomar el mínimo de una división por 2 n . Si el número binario se trata como complemento a uno , entonces la misma operación de desplazamiento hacia la derecha da como resultado una división por 2 n y un redondeo hacia cero .
Cambio lógico
 |  |
En un desplazamiento lógico , se desplazan ceros para reemplazar los bits descartados. Por lo tanto, los desplazamientos lógicos y aritméticos a la izquierda son exactamente iguales.
Sin embargo, como el desplazamiento lógico a la derecha inserta bits de valor 0 en el bit más significativo, en lugar de copiar el bit de signo, es ideal para números binarios sin signo, mientras que el desplazamiento aritmético a la derecha es ideal para números binarios de complemento a dos con signo.
Cambio circular
Otra forma de desplazamiento es el desplazamiento circular , rotación bit a bit o rotación de bits .
Girar
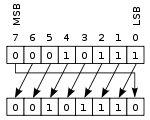 | 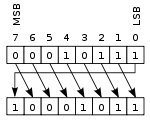 |
En esta operación, a veces llamada rotación sin acarreo , los bits se "rotan" como si los extremos izquierdo y derecho del registro estuvieran unidos. El valor que se desplaza hacia la derecha durante un desplazamiento a la izquierda es el valor que se desplazó hacia la izquierda, y viceversa para una operación de desplazamiento a la derecha. Esto es útil si es necesario conservar todos los bits existentes y se utiliza con frecuencia en criptografía digital . [ Aclaración necesaria ]
Girar a través del transporte
 |  |
Rotar a través de acarreo es una variante de la operación de rotación, donde el bit que se desplaza hacia adentro (en cualquier extremo) es el valor antiguo del indicador de acarreo, y el bit que se desplaza hacia afuera (en el otro extremo) se convierte en el nuevo valor del indicador de acarreo.
Una única rotación a través del acarreo puede simular un desplazamiento lógico o aritmético de una posición configurando el indicador de acarreo de antemano. Por ejemplo, si el indicador de acarreo contiene 0, entonces x RIGHT-ROTATE-THROUGH-CARRY-BY-ONEes un desplazamiento lógico a la derecha, y si el indicador de acarreo contiene una copia del bit de signo, entonces x RIGHT-ROTATE-THROUGH-CARRY-BY-ONEes un desplazamiento aritmético a la derecha. Por este motivo, algunos microcontroladores, como los PIC de gama baja, solo tienen rotación y rotación a través del acarreo , y no se molestan con las instrucciones de desplazamiento aritmético o lógico.
La rotación a través del acarreo es especialmente útil cuando se realizan cambios en números mayores que el tamaño de palabra nativo del procesador , porque si se almacena un número grande en dos registros, el bit que se desplaza de un extremo del primer registro debe ingresar en el otro extremo del segundo. Con la rotación a través del acarreo, ese bit se "guarda" en el indicador de acarreo durante el primer cambio, listo para ingresar durante el segundo cambio sin ninguna preparación adicional.
En lenguajes de alto nivel
En la familia de lenguajes C
En los lenguajes C y C++, los operadores de desplazamiento lógico son " <<" para desplazamiento a la izquierda y " >>" para desplazamiento a la derecha. La cantidad de posiciones a desplazar se proporciona como segundo argumento del operador. Por ejemplo,
x = y << 2 ; asigna xel resultado de desplazar yhacia la izquierda dos bits, lo que equivale a una multiplicación por cuatro.
Los desplazamientos pueden dar como resultado un comportamiento definido por la implementación o un comportamiento indefinido , por lo que se debe tener cuidado al usarlos. El resultado de desplazar un número de bits mayor o igual al tamaño de la palabra es un comportamiento indefinido en C y C++. [2] [3] El desplazamiento a la derecha de un valor negativo está definido por la implementación y no se recomienda según las buenas prácticas de codificación; [4] el resultado de desplazar a la izquierda un valor con signo es indefinido si el resultado no se puede representar en el tipo de resultado. [2]
En C#, el desplazamiento a la derecha es un desplazamiento aritmético cuando el primer operando es un int o long. Si el primer operando es de tipo uint o ulong, el desplazamiento a la derecha es un desplazamiento lógico. [5]
Cambios circulares
La familia de lenguajes C carece de un operador de rotación (aunque C++20 proporciona std::rotly std::rotr), pero se puede sintetizar uno a partir de los operadores de desplazamiento. Se debe tener cuidado para garantizar que la declaración esté bien formada para evitar comportamientos indefinidos y ataques de tiempo en software con requisitos de seguridad. [6] Por ejemplo, una implementación ingenua que rota a la izquierda un valor sin signo de 32 bits xpor nposiciones es simplemente
uint32_t x = ..., n = ...; uint32_t y = ( x << n ) | ( x >> ( 32 - n )); Sin embargo, un cambio de 0bits da como resultado un comportamiento indefinido en la expresión de la derecha (x >> (32 - n))porque 32 - 0es 32y 32está fuera del rango 0-31 inclusive. Un segundo intento podría dar como resultado
uint32_t x = ..., n = ...; uint32_t y = n ? ( x << n ) | ( x >> ( 32 - n )) : x ; donde se prueba la cantidad de desplazamiento para garantizar que no introduzca un comportamiento indefinido. Sin embargo, la bifurcación agrega una ruta de código adicional y presenta una oportunidad para el análisis y ataque de tiempos, lo que a menudo no es aceptable en software de alta integridad. [6] Además, el código se compila en múltiples instrucciones de máquina, lo que a menudo es menos eficiente que la instrucción nativa del procesador.
Para evitar el comportamiento indefinido y las bifurcaciones en GCC y Clang , se recomienda lo siguiente. Muchos compiladores reconocen el patrón y el compilador emitirá una única instrucción de rotación: [7] [8] [9]
uint32_t x = ..., n = ...; uint32_t y = ( x << n ) | ( x >> ( - n & 31 )); También hay intrínsecos específicos del compilador que implementan cambios circulares , como _rotl8, _rotl16, _rotr8, _rotr16 en Microsoft Visual C++ . Clang proporciona algunos intrínsecos de rotación para compatibilidad con Microsoft que sufre los problemas anteriores. [9] GCC no ofrece intrínsecos de rotación. Intel también proporciona intrínsecos x86.
Java
En Java , todos los tipos de números enteros tienen signo, por lo que los operadores " <<" y " >>" realizan desplazamientos aritméticos. Java agrega el operador " >>>" para realizar desplazamientos lógicos a la derecha, pero como las operaciones de desplazamiento lógico y aritmético a la izquierda son idénticas para los números enteros con signo, no existe <<<el operador " " en Java.
Más detalles de los operadores de desplazamiento de Java: [10]
- Los operadores
<<(desplazamiento a la izquierda),>>(desplazamiento a la derecha con signo) y>>>(desplazamiento a la derecha sin signo) se denominan operadores de desplazamiento . - El tipo de la expresión de desplazamiento es el tipo promocionado del operando de la izquierda. Por ejemplo,
aByte >>> 2es equivalente a .((int) aByte) >>> 2 - Si el tipo promocionado del operando de la izquierda es int, solo se utilizan los cinco bits de orden más bajo del operando de la derecha como distancia de desplazamiento. Es como si el operando de la derecha estuviera sujeto a un operador AND lógico bit a bit & con el valor de máscara 0x1f (0b11111). [11] Por lo tanto, la distancia de desplazamiento realmente utilizada siempre está en el rango de 0 a 31, inclusive.
- Si el tipo promocionado del operando de la izquierda es largo, entonces solo se utilizan los seis bits de orden más bajo del operando de la derecha como distancia de desplazamiento. Es como si el operando de la derecha estuviera sujeto a un operador AND lógico bit a bit & con el valor de máscara 0x3f (0b111111). [11] Por lo tanto, la distancia de desplazamiento realmente utilizada siempre está en el rango de 0 a 63, inclusive.
- El valor de
n >>> sson n posiciones de bit desplazadas a la derecha con extensión cero. - En las operaciones de bit y de desplazamiento, el tipo
bytese convierte implícitamente aint. Si el valor del byte es negativo, el bit más alto es uno, y luego se utilizan unos para completar los bytes adicionales en el int. Por lo tanto, el resultado será .byte b1 = -5; int i = b1 | 0x0200;i == -5
JavaScript
JavaScript utiliza operaciones bit a bit para evaluar cada una de dos o más unidades en 1 o 0. [12]
Pascal
En Pascal, así como en todos sus dialectos (como Object Pascal y Standard Pascal ), los operadores lógicos de desplazamiento a la izquierda y a la derecha son " shl" y " shr", respectivamente. Incluso para números enteros con signo, shrse comporta como un desplazamiento lógico y no copia el bit de signo. El número de posiciones a desplazar se proporciona como segundo argumento. Por ejemplo, lo siguiente asigna a x el resultado de desplazar y a la izquierda dos bits:
x := y shl 2 ; Otro
- popcount , utilizado en criptografía
- contar los ceros iniciales
Aplicaciones
Las operaciones bit a bit son necesarias particularmente en la programación de nivel inferior, como controladores de dispositivos, gráficos de bajo nivel, ensamblaje de paquetes de protocolos de comunicaciones y decodificación.
Aunque las máquinas suelen tener instrucciones integradas eficientes para realizar operaciones aritméticas y lógicas, todas estas operaciones se pueden realizar combinando los operadores bit a bit y la prueba de cero de varias maneras. [13] Por ejemplo, aquí hay una implementación de pseudocódigo de la multiplicación egipcia antigua que muestra cómo multiplicar dos números enteros arbitrarios ay b( amayor que b) usando solo desplazamientos de bits y suma:
c ← 0 mientras b ≠ 0 si ( b y 1 ) ≠ 0 c ← c + a desplazar a a por 1 desplazamiento a a por 1 devuelve c Otro ejemplo es una implementación de pseudocódigo de la suma, que muestra cómo calcular la suma de dos números enteros ay busar operadores bit a bit y pruebas de cero:
mientras a ≠ 0 c ← b y a b ← b xor un desplazamiento a la izquierda c por 1 a ← c devuelve b Álgebra de Boole
A veces resulta útil simplificar expresiones complejas formadas por operaciones bit a bit, por ejemplo, al escribir compiladores. El objetivo de un compilador es traducir un lenguaje de programación de alto nivel al código de máquina más eficiente posible. El álgebra booleana se utiliza para simplificar expresiones complejas bit a bit.
Y
x & y = y & xx & (y & z) = (x & y) & zx & 0xFFFF = x[14]x & 0 = 0
x & x = x
O
x | y = y | xx | (y | z) = (x | y) | zx | 0 = xx | 0xFFFF = 0xFFFFx | x = x
NO
~(~x) = x
O-X
x ^ y = y ^ xx ^ (y ^ z) = (x ^ y) ^ zx ^ 0 = xx ^ y ^ y = xx ^ x = 0x ^ 0xFFFF = ~x
Además, XOR se puede componer utilizando las 3 operaciones básicas (AND, OR, NOT)
a ^ b = (a | b) & (~a | ~b)a ^ b = (a & ~b) | (~a & b)
Otros
x | (x & y) = xx & (x | y) = x~(x | y) = ~x & ~y~(x & y) = ~x | ~yx | (y & z) = (x | y) & (x | z)x & (y | z) = (x & y) | (x & z)x & (y ^ z) = (x & y) ^ (x & z)x + y = (x ^ y) + ((x & y) << 1)x - y = ~(~x + y)
Inversas y resolución de ecuaciones
Puede resultar difícil resolver variables en el álgebra de Boole porque, a diferencia del álgebra regular, varias operaciones no tienen inversas. Las operaciones sin inversas pierden algunos de los bits de datos originales cuando se realizan y no es posible recuperar esta información faltante.
- Tiene inversa
- NO
- O-X
- Girar a la izquierda
- Girar a la derecha
- Sin inversa
- Y
- O
- Desplazarse a la izquierda
- Desplazarse a la derecha
Orden de operaciones
Las operaciones que se encuentran en la parte superior de esta lista se ejecutan primero. Consulte el artículo principal para obtener una lista más completa.
( )~ -[15]* / %+ -[16]<< >>&^|
Véase también
Referencias
- ^ "Blog de diseño de bajo consumo de CMicrotek". CMicrotek . Consultado el 12 de agosto de 2015 .
- ^ ab JTC1/SC22/WG14 N843 "Lenguaje de programación C", sección 6.5.7
- ^ "Operadores aritméticos - cppreference.com". en.cppreference.com . Consultado el 6 de julio de 2016 .
- ^ "INT13-C. Utilice operadores bit a bit solo en operandos sin signo". CERT: Estándares de codificación segura . Instituto de Ingeniería de Software, Universidad Carnegie Mellon . Consultado el 7 de septiembre de 2015 .
- ^ "Operador (referencia de C#)". Microsoft . Consultado el 14 de julio de 2013 .
- ^ ab "¿Una rotación en tiempo casi constante que no viole los estándares?". Stack Exchange Network . Consultado el 12 de agosto de 2015 .
- ^ "Optimización deficiente del lenguaje rotatorio portátil". Proyecto GNU GCC . Consultado el 11 de agosto de 2015 .
- ^ "¿Rotación circular que no viola el estándar C/C++?". Foros para desarrolladores de Intel . Consultado el 12 de agosto de 2015 .
- ^ ab "La constante no se propaga al ensamblado en línea, lo que da como resultado "la restricción 'I' espera una expresión constante entera"". Proyecto LLVM . Consultado el 11 de agosto de 2015 .
- ^ La especificación del lenguaje Java, sección 15.19. Operadores de desplazamiento
- ^ ab "Capítulo 15. Expresiones". oracle.com .
- ^ "JavaScript bit a bit". W3Schools.com .
- ^ "Sintetización de operaciones aritméticas mediante trucos de desplazamiento de bits". Bisqwit.iki.fi. 15 de febrero de 2014. Consultado el 8 de marzo de 2014 .
- ^ A lo largo de este artículo, 0xFFFF significa que todos los bits de su tipo de datos deben establecerse en 1. La cantidad exacta de bits depende del ancho del tipo de datos.
- ^ - es negación aquí, no resta
- ^ - es una resta aquí, no una negación
Enlaces externos
- La calculadora bit a bit en línea admite operaciones bit a bit AND, OR y XOR
- XORcat, una herramienta para archivos/flujos XOR bit a bit
- División mediante desplazamientos de bits
- "Operaciones Bitwise Mod N" por Enrique Zeleny, Proyecto Demostraciones Wolfram .
- "Gráficos de composiciones de operaciones bit a bit" por Enrique Zeleny, The Wolfram Demonstrations Project.




![{\displaystyle {\begin{aligned}\operatorname {NO} x&=\sum _{n=0}^{\lfloor \log _{2}(x)\rfloor }2^{n}\left[\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}+1\right){\bmod {2}}\right]=2^{\left\lfloor \log _{2}(x)\right\rfloor +1}-1-x\\x\operatorname {Y} y&=\sum _{n=0}^{\lfloor \log _{2}(x)\rfloor }2^{n}\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)\\x\nombredeloperador {O} y&=\suma _{n=0}^{\lfloor \log _{2}(x)\rfloor }2^{n}\left(\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)+\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)-\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)\right)\\x\nombredeloperador {XOR} y&=\suma _{n=0}^{\lfloor \log _{2}(x)\rfloor }2^{n}\left(\left[\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)+\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)\right]{\bmod {2}}\right)=\sum _{n=0}^{\lfloor \log _{2}(x)\rfloor }2^{n}\left[\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor +\left\lfloor {\frac {y}{2^{n}}}\right\rfloor \right){\bmod {2}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b873908a8c81ef7d63805b77756dbcf70a03b39c)