Líneas de Kikuchi (física)
Patrones formados por dispersión
Mapa de pares de líneas de Kikuchi hasta 1/1Å para electrones de 300 keV en zafiro hexagonal (Al 2 O 3 ), con algunas intersecciones etiquetadas

Las líneas de Kikuchi son patrones de electrones formados por dispersión. Se aparean para formar bandas en la difracción de electrones a partir de muestras de un solo cristal, y sirven como "caminos en el espacio de orientación" para los microscopistas que no están seguros de lo que están mirando. En los microscopios electrónicos de transmisión , se ven fácilmente en la difracción de regiones de la muestra lo suficientemente gruesas para la dispersión múltiple. [1] A diferencia de los puntos de difracción, que parpadean cuando uno inclina el cristal, las bandas de Kikuchi marcan el espacio de orientación con intersecciones bien definidas (llamadas zonas o polos), así como caminos que conectan una intersección con la siguiente.

Los mapas experimentales y teóricos de la geometría de la banda de Kikuchi, así como sus análogos en el espacio directo, por ejemplo, los contornos de curvatura, los patrones de canalización de electrones y los mapas de visibilidad de franjas, son herramientas cada vez más útiles en la microscopía electrónica de materiales cristalinos y nanocristalinos. [2] Debido a que cada línea de Kikuchi está asociada con la difracción de Bragg desde un lado de un solo conjunto de planos reticulares, estas líneas se pueden etiquetar con los mismos índices de Miller o de red recíproca que se utilizan para identificar puntos de difracción individuales. Las intersecciones o zonas de la banda de Kikuchi, por otro lado, se indexan con índices de red directa, es decir, índices que representan múltiplos enteros de los vectores de base de la red a , b y c .

Las líneas de Kikuchi se forman en patrones de difracción por electrones difusamente dispersos, por ejemplo, como resultado de vibraciones térmicas de los átomos. [3] Las principales características de su geometría se pueden deducir de un mecanismo elástico simple propuesto en 1928 por Seishi Kikuchi , [4] aunque se necesita la teoría dinámica de la dispersión inelástica difusa para comprenderlas cuantitativamente. [5]

En la dispersión de rayos X, estas líneas se denominan líneas de Kossel [6] (llamadas así en honor a Walther Kossel ).

Registro de patrones y mapas experimentales de Kikuchi

Líneas de Kikuchi en un patrón de difracción de haz convergente de silicio monocristalino tomadas con un haz de electrones de 300 keV

La figura de la izquierda muestra las líneas de Kikuchi que conducen a una zona de silicio [100], tomadas con la dirección del haz aproximadamente a 7,9° de la zona a lo largo de la banda de Kikuchi (004). El rango dinámico en la imagen es tan grande que solo algunas partes de la película no están sobreexpuestas . Las líneas de Kikuchi son mucho más fáciles de seguir con ojos adaptados a la oscuridad en una pantalla fluorescente que de capturarlas inmóviles en papel o película, a pesar de que tanto los ojos como los medios fotográficos tienen una respuesta aproximadamente logarítmica a la intensidad de la iluminación. Por lo tanto, el trabajo completamente cuantitativo sobre tales características de difracción se ve asistido por el gran rango dinámico lineal de los detectores CCD . [7]

Esta imagen abarca un rango angular de más de 10° y requirió el uso de una cámara de longitud L más corta de lo habitual . Los anchos de banda de Kikuchi en sí mismos (aproximadamente λL/d donde λ/d es aproximadamente el doble del ángulo de Bragg para el plano correspondiente) están muy por debajo de 1°, porque la longitud de onda λ de los electrones (aproximadamente 1,97 picómetros en este caso) es mucho menor que el espaciado d del plano reticular en sí. A modo de comparación, el espaciado d para el silicio (022) es de aproximadamente 192 picómetros, mientras que el espaciado d para el silicio (004) es de aproximadamente 136 picómetros.

La imagen se tomó de una región del cristal que es más gruesa que el camino libre medio inelástico (aproximadamente 200 nanómetros), de modo que las características de dispersión difusa (las líneas de Kikuchi) serían fuertes en comparación con las características de dispersión coherente (puntos de difracción). El hecho de que los puntos de difracción supervivientes aparezcan como discos intersectados por líneas de Kikuchi brillantes significa que el patrón de difracción se tomó con un haz de electrones convergente. En la práctica, las líneas de Kikuchi se ven fácilmente en regiones gruesas de patrones de difracción de electrones de área seleccionada o de haz convergente , pero son difíciles de ver en la difracción de cristales de mucho menos de 100 nm de tamaño (donde los efectos de visibilidad de la franja reticular se vuelven importantes). Esta imagen se registró en haz convergente, porque eso también reduce el rango de contrastes que deben registrarse en película.

Para compilar mapas de Kikuchi que cubran más de un estereorradián es necesario tomar muchas imágenes con inclinaciones que se modifican solo de manera incremental (por ejemplo, 2° en cada dirección). Esto puede ser un trabajo tedioso, pero puede ser útil cuando se investiga un cristal con una estructura desconocida, ya que puede revelar claramente la simetría reticular en tres dimensiones. [8]

Mapas lineales de Kikuchi y su proyección estereográfica

[001] Mapa estereográfico de Kikuchi de zona para cristales cúbicos centrados en las caras de diamante
Animación del recorrido de inclinación entre cuatro de las ocho zonas <111> en un cristal fcc

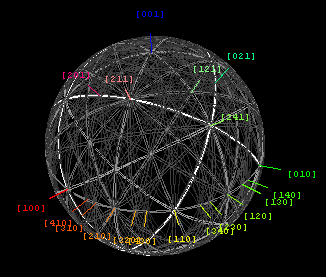
La figura de la izquierda representa las líneas de Kikuchi para una sección más grande del espacio de orientación del silicio. El ángulo subtendido entre las grandes zonas [011] y [001] en la parte inferior es de 45° para el silicio. Nótese que la zona cuádruple en la parte inferior derecha (aquí etiquetada como [001]) tiene la misma simetría y orientación que la zona etiquetada como [100] en el patrón experimental anterior, aunque ese patrón experimental solo subtiende aproximadamente 10°.

Obsérvese también que la figura de la izquierda está extraída de una proyección estereográfica centrada en esa zona [001]. Dichas proyecciones conformes permiten trazar trozos de superficie esférica sobre un plano, conservando al mismo tiempo los ángulos locales de intersección y, por lo tanto, las simetrías de zona. Para trazar dichos mapas es necesario poder dibujar arcos de círculos con un radio de curvatura muy grande. La figura de la izquierda, por ejemplo, se dibujó antes de la llegada de las computadoras y, por lo tanto, requirió el uso de una brújula de haz . Encontrar una brújula de haz hoy en día puede ser bastante difícil, ya que es mucho más fácil dibujar curvas que tengan un radio de curvatura grande (en dos o tres dimensiones) con la ayuda de una computadora.

El efecto de conservación del ángulo de los gráficos estereográficos es aún más obvio en la figura de la derecha, que abarca 180° completos del espacio de orientación de un cristal cúbico o centrado en las caras, como el del oro o el aluminio. La animación sigue las bandas de visibilidad de franjas {220} de ese cristal cúbico centrado en las caras entre las zonas <111>, en cuyo punto la rotación de 60° establece el viaje a la siguiente zona <111> a través de una repetición de la secuencia original. Las bandas de visibilidad de franjas tienen la misma geometría global que las bandas de Kikuchi, pero para muestras delgadas su ancho es proporcional (en lugar de inversamente proporcional) al espaciado d. Aunque el ancho del campo angular (y el rango de inclinación) obtenible experimentalmente con las bandas de Kikuchi es generalmente mucho menor, la animación ofrece una vista de gran angular de cómo las bandas de Kikuchi ayudan a los cristalógrafos informados a encontrar su camino entre los puntos de referencia en el espacio de orientación de una muestra de cristal único.

Análogos del espacio real

Una araña de contorno de curvatura de silicio [100], atrapada sobre una región elíptica de aproximadamente 500 nanómetros de ancho

Las líneas de Kikuchi sirven para resaltar el borde de los planos de la red en imágenes de difracción de muestras más gruesas. Debido a que los ángulos de Bragg en la difracción de electrones de alta energía son muy pequeños (~ 1 ⁄ 4 grados para 300 keV), las bandas de Kikuchi son bastante estrechas en el espacio recíproco. Esto también significa que en las imágenes del espacio real, los planos de la red de borde no están decorados por características de dispersión difusa sino por el contraste asociado con la dispersión coherente. Estas características de dispersión coherente incluyen difracción adicional (responsable de los contornos de curvatura en láminas curvas), mayor penetración de electrones (que da lugar a patrones de canalización de electrones en imágenes de electrones de barrido de superficies de cristal) y contraste de franjas de la red (que da como resultado una dependencia de la intensidad de las franjas de la red en la orientación del haz que está vinculada al espesor de la muestra). Aunque los detalles del contraste difieren, la geometría de traza del plano de la red de estas características y de los mapas de Kikuchi son las mismas.

Curvas de curvas y oscilaciones

Visibilidad del contorno de curvatura y de la franja reticular en función del espesor de la muestra y de la inclinación del haz

Las curvas oscilantes [9] (izquierda) son gráficos de la intensidad de los electrones dispersos, como una función del ángulo entre un haz de electrones incidente y la normal a un conjunto de planos reticulares en la muestra. A medida que este ángulo cambia en cualquier dirección desde el borde (orientación en la que el haz de electrones corre paralelo a los planos reticulares y perpendicular a su normal), el haz pasa a la condición de difracción de Bragg y más electrones se difractan fuera de la apertura del plano focal posterior del microscopio , lo que da lugar a los pares de líneas oscuras (bandas) que se ven en la imagen de la lámina de silicio doblada que se muestra en la imagen de la derecha.

La "araña" del contorno de curvatura [100] de esta imagen, atrapada en una región de silicio que tenía la forma de un vidrio de reloj ovalado de menos de un micrómetro de tamaño, fue fotografiada con electrones de 300 keV. Si inclina el cristal, la araña se mueve hacia los bordes del óvalo como si estuviera tratando de salir. Por ejemplo, en esta imagen la intersección [100] de la araña se ha movido hacia el lado derecho de la elipse a medida que la muestra se inclinó hacia la izquierda.

Las patas de la araña y sus intersecciones se pueden indexar como se muestra exactamente de la misma manera que el patrón de Kikuchi cerca de [100] en la sección sobre patrones de Kikuchi experimentales anterior. En principio, se podría utilizar este contorno de curvatura para modelar la inclinación vectorial de la lámina (con precisión de milirradianes ) en todos los puntos del óvalo.

Mapas de visibilidad de franjas reticulares

Como se puede ver en la curva de oscilación anterior, a medida que el espesor de la muestra se mueve hacia el rango de 10 nanómetros y más pequeños (por ejemplo, para electrones de 300 keV y espaciamientos reticulares cercanos a 0,23 nm), el rango angular de inclinaciones que dan lugar a la difracción y/o al contraste de franjas reticulares se vuelve inversamente proporcional al espesor de la muestra. Por lo tanto, la geometría de la visibilidad de las franjas reticulares se vuelve útil en el estudio de nanomateriales con microscopio electrónico , [10] [11] al igual que los contornos de curvatura y las líneas de Kikuchi son útiles en el estudio de muestras de monocristales (por ejemplo, muestras de metales y semiconductores con espesor en el rango de décimas de micrómetro). Las aplicaciones a la nanoestructura incluyen, por ejemplo: (i) determinar los parámetros reticulares 3D de nanopartículas individuales a partir de imágenes tomadas con diferentes inclinaciones, [12] (ii) huellas de franjas de colecciones de nanopartículas orientadas aleatoriamente, (iii) mapas de espesor de partículas basados ​​en cambios de contraste de franjas bajo inclinación, (iv) detección de maclado icosaédrico a partir de la imagen reticular de una nanopartícula orientada aleatoriamente, y (v) análisis de las relaciones de orientación entre nanopartículas y un soporte cilíndrico.

Patrones de canalización de electrones

Construcción de la zona de Brillouin con electrones de 300 keV

Todas las técnicas anteriores implican la detección de electrones que han pasado a través de una muestra delgada, generalmente en un microscopio electrónico de transmisión . Los microscopios electrónicos de barrido , por otro lado, generalmente observan los electrones "levantados" cuando se pasa un haz de electrones enfocado a través de una muestra gruesa. Los patrones de canalización de electrones son efectos de contraste asociados con planos reticulares de borde que aparecen en imágenes de electrones secundarios y/o retrodispersados ​​del microscopio electrónico de barrido.

Los efectos de contraste son similares en primer orden a los de los contornos de curvatura, es decir, los electrones que entran en una superficie cristalina en condiciones de difracción tienden a canalizarse (penetrar más profundamente en la muestra sin perder energía) y, por lo tanto, hacen que se desplacen menos electrones cerca de la superficie de entrada para su detección. Por lo tanto, se forman bandas, según la orientación del haz/red, con la geometría de línea de Kikuchi, ahora conocida.

La primera imagen obtenida mediante microscopio electrónico de barrido (MEB) fue una imagen de contraste de canalización de electrones en acero al silicio . [13] Sin embargo, los usos prácticos de la técnica son limitados porque, por lo general, solo una fina capa de daño por abrasión o un revestimiento amorfo es suficiente para ocultar el contraste. [14] Si fuera necesario aplicar un revestimiento conductor a la muestra antes de examinarla para evitar la carga, esto también podría ocultar el contraste. En superficies hendidas y superficies autoensambladas a escala atómica, es probable que los patrones de canalización de electrones se apliquen cada vez más en los microscopios modernos en los próximos años.

Véase también

Referencias

  1. ^ David B. Williams; C. Barry Carter (1996). Microscopía electrónica de transmisión: un libro de texto para la ciencia de los materiales . Plenum Press, NY. ISBN 978-0-306-45324-3.
  2. ^ K. Saruwatari; J. Akai; Y. Fukumori; N. Ozaki; H. Nagasawa; T. Kogure (2008). "Análisis de orientación cristalina de biominerales utilizando patrones Kikuchi en TEM". J.Mineral. Gasolina. Ciencia . 103 : 16-22. doi : 10.2465/jmps.070611 .
  3. ^ Earl J. Kirkland (1998). Computación avanzada en microscopía electrónica . Plenum Press, NY. p. 151. ISBN 978-0-306-45936-8.
  4. ^ S. Kikuchi (1928). "Difracción de rayos catódicos por mica". Revista japonesa de física . 5 (3061): 83–96. Código Bibliográfico :1928Natur.121.1019N. doi :10.1038/1211019a0.
  5. ^ P. Hirsch; A. Howie; R. Nicholson; DW Pashley; MJ Whelan (1977). Microscopía electrónica de cristales delgados . Butterworths/Krieger, Londres/Malabar FL. ISBN 978-0-88275-376-8.
  6. ^ RW James (1982). "Capítulo VIII". Los principios ópticos de la difracción de rayos X. Prensa Ox Bow, Woodbridge, Connecticut. ISBN 978-0-918024-23-7.
  7. ^ JCH Spence y J. Zuo (1992). "Cap. 9". Microdifracción de electrones . Plenum, Nueva York. ISBN 978-0-306-44262-9.
  8. ^ E. Levine; WL Bell; G. Thomas (1966). "Otras aplicaciones de los patrones de difracción de Kikuchi; mapas de Kikuchi". Revista de Física Aplicada . 37 (5): 2141–2148. Código Bibliográfico :1966JAP....37.2141L. doi :10.1063/1.1708749.
  9. ^ H. Hashimoto; A. Howie; MJ Whelan (1962). "Efectos anómalos de absorción de electrones en láminas metálicas: teoría y comparación con experimentos". Actas de la Royal Society A . 269 (1336): 80. Bibcode :1962RSPSA.269...80H. doi :10.1098/rspa.1962.0164. S2CID  97942498.
  10. ^ P. Fraundorf; Wentao Qin; P. Moeck; Eric Mandell (2005). "Dando sentido a las franjas de la red de nanocristales". Journal of Applied Physics . 98 (11): 114308–114308–10. arXiv : cond-mat/0212281 . Código Bibliográfico :2005JAP....98k4308F. doi :10.1063/1.2135414. S2CID  13681236.
  11. ^ P. Wang; AL Bleloch; U. Falke; PJ Goodhew (2006). "Aspectos geométricos de la visibilidad del contraste de red en materiales nanocristalinos utilizando HAADF STEM". Ultramicroscopía . 106 (4–5): 277–283. doi :10.1016/j.ultramic.2005.09.005.
  12. ^ Wentao Qin; P. Fraundorf (2003). "Parámetros de red a partir de imágenes de espacio directo en dos inclinaciones". Ultramicroscopía . 94 (3–4): 245–262. arXiv : cond-mat/0001139 . doi :10.1016/S0304-3991(02)00335-2. PMID  12524195. S2CID  10524417.
  13. ^ Knoll M. (1935). "Aufladepotentiel und sekundäremission elektronenbestrahlter körper (potencial estático y emisión secundaria de cuerpos bajo irradiación de electrones)". Z. Tecnología. Física . 11 : 467–475.
  14. ^ JI Goldstein; DE Newbury; P. Echlin; DC Joy; AD Romig Jr.; CE Lyman; C. Fiori; E. Lifshin (1992). Microscopía electrónica de barrido y microanálisis de rayos X. Plenum Press, NY. ISBN 978-0-306-44175-2.
  • Calcular patrones con WebEMApS en UIUC .
  • Algunos mapas 3D interactivos en UM Saint Louis .
  • Calcule el mapa o patrones de Kikuchi con el software gratuito PTCLab [1].
Obtenido de "https://es.wikipedia.org/w/index.php?title=Líneas_de_Kikuchi_(física)&oldid=1228203348"